13.3.1.1 等腰三角形的性质同步练习 (含答案)
文档属性
| 名称 | 13.3.1.1 等腰三角形的性质同步练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 19:48:02 | ||
图片预览



文档简介
13.3.1等腰三角形
第1课时 等腰三角形的性质
【知识重点】
知识点1 等腰三角形的定义
定义 有两边相等的三角形是等腰三角形.
几何语言:如图,在△ABC中,
∵ AB=AC,∴△ABC为等腰三角形.
等腰三角形的顶角可以是锐角、直角或钝角,
但底角只能是锐角. 根据顶角的大小,等腰三角形可分为等腰锐角三角形、等腰直角三角形和等腰钝角三角形.
特别解读
确定等腰三角形的两条腰时,应找三角形中相等的两边,腰与三角形本身的位置无关.
知识点2 等腰三角形的性质
1. 性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
几何语言:如图,在△ABC中,
∵ AB=AC,∴∠B=∠C.
特别提醒
① 适用条件:必须在同一个三角形中.
② 作用:是证明角相等的常用方法,应用它证角相等时可省去三角形全等的证明,因而更简便.
2. 性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).
几何语言:如图,在△ABC中,
(1)∵ AB=AC,AD⊥BC,
∴ AD平分∠BAC(或BD=CD);
(2)∵ AB=AC,BD=DC,∴ AD⊥BC(或AD平分∠BAC);
(3)∵ AB=AC,AD平分∠BAC,∴ BD=DC(或AD⊥BC).
特别解读
① 适用条件:
(a)必须是等腰三角形;
(b)必须是底边上的中线、底边上的高和顶角的平分线才相互重合.
② 作用:是证明线段相等、角相等、线段垂直等关系的重要方法.
3. 对称性 等腰三角形是轴对称图形,顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴.
【经典例题】
【例1】若某个等腰三角形的两边长分别为4和6,求这个等腰三角形的周长.
解题秘方:根据等腰三角形的定义确定腰和底边的长,再利用三角形三边关系进行判断并计算.
特别提醒:等腰三角形的边分腰和底边,若没有说明,则必须分类讨论,同时注意三角形的三边关系.
【例2】如图,在△ABC中,AB=AC,AD平分∠BAC.
(1)求∠ADB的度数;
(2)若∠BAC=100°,求∠B,∠C的度数;
(3)若BC=3 cm,求BD的长.
解题秘方:紧扣等腰三角形的性质进行解答.
【例3】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高. 求证:BD=CE.
解题秘方:利用等腰三角形的边角性质为证明△BEC和△CDB全等创造条件.
【例4】如图,在△ABC中,AB=AC,点D,E分别在AC,AB边上,且BC=BD,AD=DE=EB,求∠A 的度数.
解题秘方:利用“等边对等角”及三角形外角的性质将△ABC中的三个角都用要求的∠A来表示,利用三角形内角和解决问题.
小结:当已知条件中没有已知度数的角而又要求角的度数时,一般采用方程思想来解决问题. 设出要求的角的度数,然后根据等腰三角形的性质以及三角形外角与内角之间的关系,用含未知数的式子表示出一个三角形的三个内角的度数,再利用三角形的内角和等于180°列出方程,求出未知数的值即可.
【同步练习】
一、选择题
1.已知等腰三角形的一个角是100°,则它的顶角是( )
A.40° B.60° C.80° D.100°
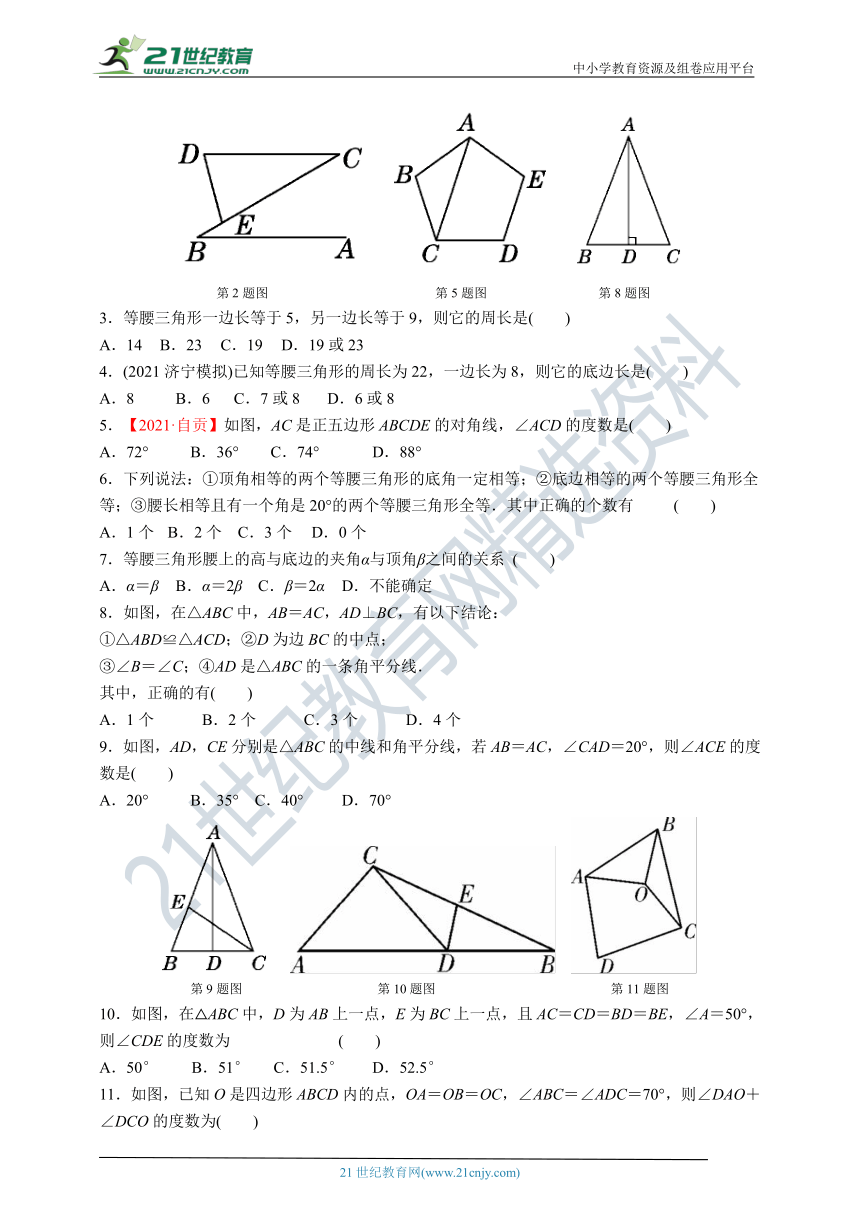
2.【2021·赤峰】如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D的度数为( )
A.85° B.75° C.65° D.30°
第2题图 第5题图 第8题图
3.等腰三角形一边长等于5,另一边长等于9,则它的周长是( )
A.14 B.23 C.19 D.19或23
4.(2021济宁模拟)已知等腰三角形的周长为22,一边长为8,则它的底边长是( )
A.8 B.6 C.7或8 D.6或8
5.【2021·自贡】如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( )
A.72° B.36° C.74° D.88°
6.下列说法:①顶角相等的两个等腰三角形的底角一定相等;②底边相等的两个等腰三角形全等;③腰长相等且有一个角是20°的两个等腰三角形全等.其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.0个
7.等腰三角形腰上的高与底边的夹角α与顶角β之间的关系 ( )
A.α=β B.α=2β C.β=2α D.不能确定
8.如图,在△ABC中,AB=AC,AD⊥BC,有以下结论:
①△ABD≌△ACD;②D为边BC的中点;
③∠B=∠C;④AD是△ABC的一条角平分线.
其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
第9题图 第10题图 第11题图
10.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为 ( )
A.50° B.51° C.51.5° D.52.5°
11.如图,已知O是四边形ABCD内的点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的度数为( )
A.70° B.110° C.140° D.150°
二、填空题
12.等腰三角形的两个________相等(简写成“等边对等角”).注意:“等边对等角”是在__________三角形中.
13.等腰三角形的顶角________、底边上的______、底边上的______相互重合(简写成“__________”).
14.已知等腰三角形的一个外角为130°,则它的顶角的度数为 .
15.【2021·滨州】如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的大小为________.
第15题图 第16题图 第17题图
16.【2021·广州】如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B′,当B′D∥AC时,则∠BCD的度数为________.
17.【2021·鞍山】如图,∠POQ=90°,定长为a的线段端点A,B分别在射线OP,OQ上运动(点A,B不与点O重合),C为AB的中点,作△OAC关于直线OC对称的△OA′C,A′O交AB于点D,当△OBD是等腰三角形时,∠OBD的度数为________.
三、解答题
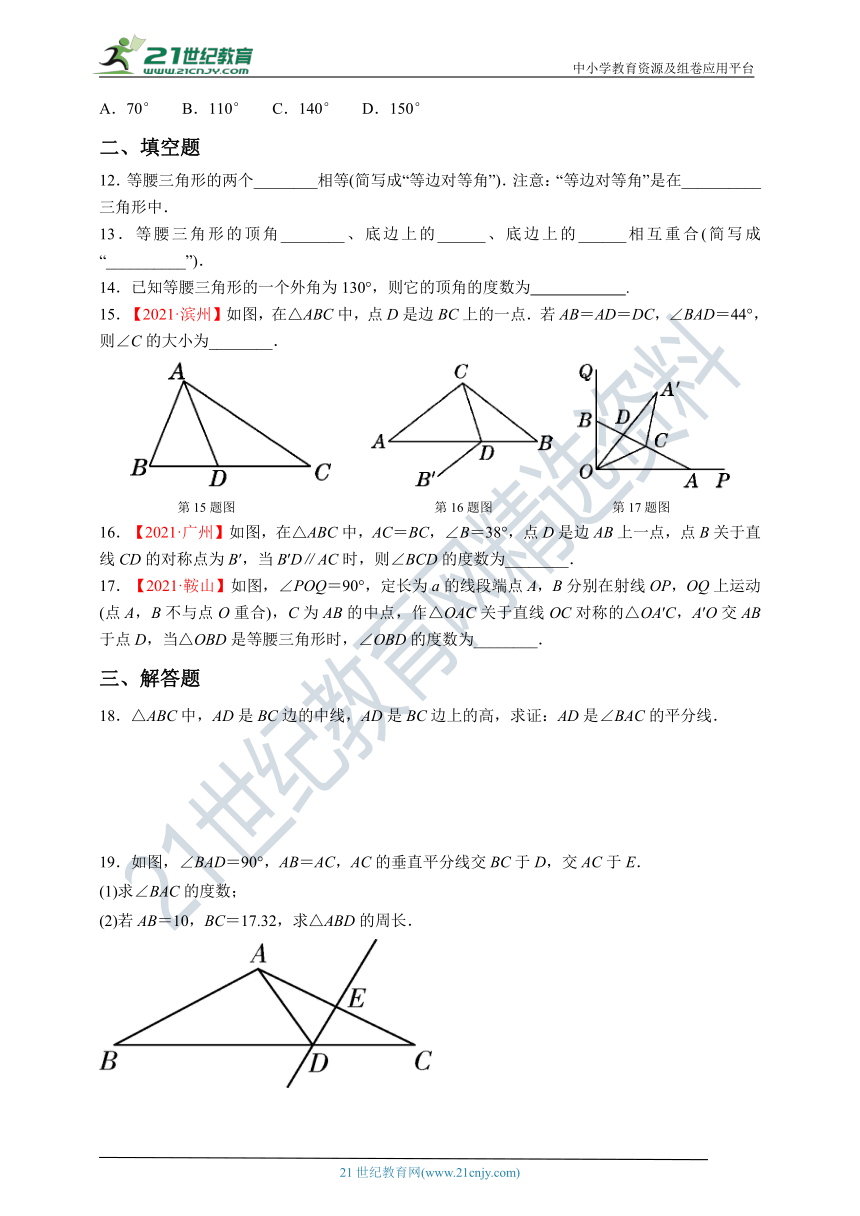
18.△ABC中,AD是BC边的中线,AD是BC边上的高,求证:AD是∠BAC的平分线.
19.如图,∠BAD=90°,AB=AC,AC的垂直平分线交BC于D,交AC于E.
(1)求∠BAC的度数;
(2)若AB=10,BC=17.32,求△ABD的周长.
20.如图,在△ABC中,AB=AC,AD是BC边上的中线,延长CB至点E,延长BC至点F,使BE=CF,连接AE,AF.
求证:AD平分∠EAF.
21.【2021·无锡】已知:如图,AC,DB相交于点O,AB=DC,∠ABO=∠DCO.求证:
(1)△ABO≌△DCO;
(2)∠OBC=∠OCB.
22.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
23.如图,△ABC中,AB=AC,D为BC边上的中点,DE⊥AB于E,DF⊥AC于F.
(1)求证:DE=DF;
(2)过B作BM⊥AC于M,D为BC的中点改为D在BC上(D不与B、C重合),其余条件不变,问DE、DF、BM的关系怎样?说明理由.
24.【2020·绍兴】问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】若某个等腰三角形的两边长分别为4和6,求这个等腰三角形的周长.
解题秘方:根据等腰三角形的定义确定腰和底边的长,再利用三角形三边关系进行判断并计算.
解:∵等腰三角形的底边长和腰长不确定,∴需分两种情况讨论. 第一种情况:当4 为腰长时,该等腰三角形的三边长分别为4,4,6,∵ 4+4>6,满足三角形的三边关系, ∴周长=4+4+6=14;第二种情况:当 6为腰长时,该等腰三角形的三边长分别为4,6,6,∵ 4+6>6,满足三角形的三边关系,∴周长=6+6+4=16.
综上可知,这个等腰三角形的周长为14或16.
特别提醒:等腰三角形的边分腰和底边,若没有说明,则必须分类讨论,同时注意三角形的三边关系.
【例2】如图,在△ABC中,AB=AC,AD平分∠BAC.
解题秘方:紧扣等腰三角形的性质进行解答.
(1)求∠ADB的度数;
解:∵ AB=AC,AD平分∠BAC,
∴ AD⊥BC,
∴∠ADB=90°.
(2)若∠BAC=100°,求∠B,∠C的度数;
解:在△ABC中,∵ AB=AC,∠BAC=100°,
∴∠B=∠C=×(180°-100°)=40°.
(3)若BC=3 cm,求BD的长.
解:∵ AB=AC,AD平分∠BAC,
∴ AD是BC边上的中线,
∴ BD=BC=×3=1.5(cm).
【例3】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高. 求证:BD=CE.
解题秘方:利用等腰三角形的边角性质为证明△BEC和△CDB全等创造条件.
证明:方法一 ∵ AB=AC,∴∠ABC=∠ACB.
∵ BD⊥AC,CE⊥AB,∴∠BDC=∠BEC=90°.
在△BEC和△CDB中,
∴△BEC≌△CDB(AAS). ∴ BD=CE.
方法二 ∵ S△ABC=AB·CE,S△ABC=AC·BD,AB=AC,∴ BD=CE.
【例4】如图,在△ABC中,AB=AC,点D,E分别在AC,AB边上,且BC=BD,AD=DE=EB,求∠A 的度数.
解题秘方:利用“等边对等角”及三角形外角的性质将△ABC中的三个角都用要求的∠A来表示,利用三角形内角和解决问题.
解:设∠A=x°,∵ AD=DE,∴∠AED=∠A=x°.
∵ DE=EB,∴∠EBD=∠BDE=x°,
∴∠BDC=∠A+∠EBD=x°.
∵ BC=BD,∴∠C=∠BDC=x°.
∵ AB=AC,∴∠ABC=∠C=x°.
∴ x+x+x=180,解得x=45. ∴∠A=45°.
小结:当已知条件中没有已知度数的角而又要求角的度数时,一般采用方程思想来解决问题. 设出要求的角的度数,然后根据等腰三角形的性质以及三角形外角与内角之间的关系,用含未知数的式子表示出一个三角形的三个内角的度数,再利用三角形的内角和等于180°列出方程,求出未知数的值即可.
【同步练习】
一、选择题
1.已知等腰三角形的一个角是100°,则它的顶角是( D )
A.40° B.60° C.80° D.100°
2.【2021·赤峰】如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D的度数为( B )
A.85° B.75° C.65° D.30°
第2题图 第5题图 第8题图
3.等腰三角形一边长等于5,另一边长等于9,则它的周长是( D )
A.14 B.23 C.19 D.19或23
4.(2021济宁模拟)已知等腰三角形的周长为22,一边长为8,则它的底边长是( D )
A.8 B.6 C.7或8 D.6或8
5.【2021·自贡】如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( A )
A.72° B.36° C.74° D.88°
6.下列说法:①顶角相等的两个等腰三角形的底角一定相等;②底边相等的两个等腰三角形全等;③腰长相等且有一个角是20°的两个等腰三角形全等.其中正确的个数有 ( A )
A.1个 B.2个 C.3个 D.0个
7.等腰三角形腰上的高与底边的夹角α与顶角β之间的关系 ( C )
A.α=β B.α=2β C.β=2α D.不能确定
8.如图,在△ABC中,AB=AC,AD⊥BC,有以下结论:
①△ABD≌△ACD;②D为边BC的中点;
③∠B=∠C;④AD是△ABC的一条角平分线.
其中,正确的有( D )
A.1个 B.2个 C.3个 D.4个
9.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( B )
A.20° B.35° C.40° D.70°
第9题图 第10题图 第11题图
10.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为 ( D )
A.50° B.51° C.51.5° D.52.5°
11.如图,已知O是四边形ABCD内的点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的度数为( D )
A.70° B.110° C.140° D.150°
二、填空题
12.等腰三角形的两个________相等(简写成“等边对等角”).注意:“等边对等角”是在__________三角形中.
【答案】底角 同一个
13.等腰三角形的顶角________、底边上的______、底边上的______相互重合(简写成“__________”).
【答案】平分线 中线 高 三线合一
14.已知等腰三角形的一个外角为130°,则它的顶角的度数为 .
【答案】50°或80°
15.【2021·滨州】如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的大小为________.
【答案】34°
第15题图 第16题图 第17题图
16.【2021·广州】如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B′,当B′D∥AC时,则∠BCD的度数为________.
【解析】∵AC=BC,∴∠A=∠B=38°.
∵∠B′D∥AC,∴∠ADB′=∠A=38°.
∵点B关于直线CD的对称点为B′,
∴∠CDB′=∠CDB=(38°+180°)=109°,
∴∠BCD=180°-∠B-∠CDB=180°-38°-109°=33°.
【答案】33°
17.【2021·鞍山】如图,∠POQ=90°,定长为a的线段端点A,B分别在射线OP,OQ上运动(点A,B不与点O重合),C为AB的中点,作△OAC关于直线OC对称的△OA′C,A′O交AB于点D,当△OBD是等腰三角形时,∠OBD的度数为________.
【解析】作AE⊥OA交OC的延长线于点E.
∵AE⊥OA,∴∠OAE=90°.
又∵∠POQ=90°,∴∠OAE=∠POQ.∴AE∥OB.
∴∠OBC=∠CAE.
∵C为AB的中点,∴BC=AC.
又∵∠BCO=∠ACE,∴△BCO≌△ACE.
∴OC=CE,OB=EA.
在△BOA和△EAO中,OB=AE,OA=AO,∠BOA=∠EAO=90°,∴△BOA≌△EAO,∴AB=OE.
∴OC=AC=BC.∴∠COA=∠BAO,∠OBC=∠BOC.
又由折叠性质可得∠COA=∠COA′.
∴∠COA=∠COA′=∠BAO.
设∠COA=∠COA′=∠BAO=x,则∠BCO=2x,∠A′OB=90°-2x,∠OBD=90°-x,∠BDO=∠AOD+∠BAO=3x.
①当OB=OD时,∠OBD=∠BDO.∴90°-x=3x.
解得x=22.5°. ∴∠OBD=90°-22.5°=67.5°.
②当BD=OD时,∠OBD=∠A′OB.
∴90°-x=90°-2x,方程无解.∴此情况不存在.
③当OB=DB时,∠BDO=∠A′OB. ∴3x=90°-2x.
解得x=18°.∴∠OBD=90°-18°=72°.
综上,∠OBD的度数为67.5°或72°.
【答案】67.5°或72°
三、解答题
18.△ABC中,AD是BC边的中线,AD是BC边上的高,求证:AD是∠BAC的平分线.
证明:由题意得,∵AD⊥BC,BD=CD,
∴AD是BC的垂直平分线.
∴AB=AC.
∵AD是BC边的中线,
∴AD是∠BAC的平分线.
19.如图,∠BAD=90°,AB=AC,AC的垂直平分线交BC于D,交AC于E.
(1)求∠BAC的度数;
(2)若AB=10,BC=17.32,求△ABD的周长.
解:(1)∵AB=AC,∴∠B=∠C,
设∠B=∠C=x°,∵∠BAD=90°,
∴∠ADB=90°-∠B=(90-x)°.
∵DE垂直平分AC,∴DA=DC,
∴∠DAC=∠C=x°,∴90-x=2x,
解得x=30,∴∠BAC=90°+30°=120°.
(2)由(1)知DA=DC,
∴△ABD的周长=AB+AD+BD=AB+BC=10+17.32=27.32.
20.如图,在△ABC中,AB=AC,AD是BC边上的中线,延长CB至点E,延长BC至点F,使BE=CF,连接AE,AF.
求证:AD平分∠EAF.
证明:∵在△ABC中,AB=AC,AD是BC边上的中线,
∴AD平分∠BAC,∠ABD=∠ACD.
∴∠BAD=∠CAD,∠ABE=∠ACF.
在△ABE和△ACF中,
∴△ABE≌△ACF(SAS).∴∠BAE=∠CAF.
∴∠BAE+∠BAD=∠CAF+∠CAD,
即∠EAD=∠FAD.∴AD平分∠EAF.
21.【2021·无锡】已知:如图,AC,DB相交于点O,AB=DC,∠ABO=∠DCO.求证:
(1)△ABO≌△DCO;
证明:在△ABO和△DCO中,
∴△ABO≌△DCO(AAS).
(2)∠OBC=∠OCB.
证明:由(1)知,△ABO≌△DCO,
∴OB=OC.∴∠OBC=∠OCB.
22.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
证明:∵∠CAF=∠BAE,∴∠EAF=∠BAC.
又∵AE=AB,AF=AC,
∴△EAF≌△BAC(SAS).∴EF=BC.
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
解:∵AB=AE,∠ABC=65°,
∴∠BAE=180°-65°×2=50°.
∵∠CAF=∠BAE,∴∠FAG=50°.
∵△EAF≌△BAC,∴∠F=∠ACB=28°.
∴∠FGC=∠FAG+∠F=50°+28°=78°.
23.如图,△ABC中,AB=AC,D为BC边上的中点,DE⊥AB于E,DF⊥AC于F.
(1)求证:DE=DF;
(2)过B作BM⊥AC于M,D为BC的中点改为D在BC上(D不与B、C重合),其余条件不变,问DE、DF、BM的关系怎样?说明理由.
(1)证明:连接AD,∵AB=AC,D是BC的中点,∴AD平分∠BAC,∵DE⊥AB,DF⊥AC,∴DE=DF;
(2)解:BM=DE+DF.理由:连接AD,∵S△ABD=AB·DE,S△ADC=AC·DF,S△ABC=BM·AC,∵S△ABD+S△ADC=S△ABC,∴AB·DE+AC·DF=BM·AC,∵AB=AC,∴DE+DF=BM.
24.【2020·绍兴】问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
解:∠DAC的度数不会改变.
理由如下:∵EA=EC,∴∠CAE=∠C.∴∠AED=2∠C.
∵∠BAE=90°,BA=BD,
∴∠BAD= (180°-∠B)= [180°-(90°-2∠C)]=45°+∠C.
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.
∴∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
解:设∠B=m°.∵BA=BD,
∴∠BAD= (180°-m°)=90°-m°.
∴∠DAE=∠BAE-∠BAD=n°-90°+m°.
∵EA=EC,∴∠EAC=∠C.∴∠AEB=2∠CAE.
∵∠AEB=180°-n°-m°,
∴∠CAE=∠AEB=90°-n°-m°.
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
第1课时 等腰三角形的性质
【知识重点】
知识点1 等腰三角形的定义
定义 有两边相等的三角形是等腰三角形.
几何语言:如图,在△ABC中,
∵ AB=AC,∴△ABC为等腰三角形.
等腰三角形的顶角可以是锐角、直角或钝角,
但底角只能是锐角. 根据顶角的大小,等腰三角形可分为等腰锐角三角形、等腰直角三角形和等腰钝角三角形.
特别解读
确定等腰三角形的两条腰时,应找三角形中相等的两边,腰与三角形本身的位置无关.
知识点2 等腰三角形的性质
1. 性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
几何语言:如图,在△ABC中,
∵ AB=AC,∴∠B=∠C.
特别提醒
① 适用条件:必须在同一个三角形中.
② 作用:是证明角相等的常用方法,应用它证角相等时可省去三角形全等的证明,因而更简便.
2. 性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).
几何语言:如图,在△ABC中,
(1)∵ AB=AC,AD⊥BC,
∴ AD平分∠BAC(或BD=CD);
(2)∵ AB=AC,BD=DC,∴ AD⊥BC(或AD平分∠BAC);
(3)∵ AB=AC,AD平分∠BAC,∴ BD=DC(或AD⊥BC).
特别解读
① 适用条件:
(a)必须是等腰三角形;
(b)必须是底边上的中线、底边上的高和顶角的平分线才相互重合.
② 作用:是证明线段相等、角相等、线段垂直等关系的重要方法.
3. 对称性 等腰三角形是轴对称图形,顶角平分线(或底边上的高、底边上的中线)所在的直线是它的对称轴.
【经典例题】
【例1】若某个等腰三角形的两边长分别为4和6,求这个等腰三角形的周长.
解题秘方:根据等腰三角形的定义确定腰和底边的长,再利用三角形三边关系进行判断并计算.
特别提醒:等腰三角形的边分腰和底边,若没有说明,则必须分类讨论,同时注意三角形的三边关系.
【例2】如图,在△ABC中,AB=AC,AD平分∠BAC.
(1)求∠ADB的度数;
(2)若∠BAC=100°,求∠B,∠C的度数;
(3)若BC=3 cm,求BD的长.
解题秘方:紧扣等腰三角形的性质进行解答.
【例3】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高. 求证:BD=CE.
解题秘方:利用等腰三角形的边角性质为证明△BEC和△CDB全等创造条件.
【例4】如图,在△ABC中,AB=AC,点D,E分别在AC,AB边上,且BC=BD,AD=DE=EB,求∠A 的度数.
解题秘方:利用“等边对等角”及三角形外角的性质将△ABC中的三个角都用要求的∠A来表示,利用三角形内角和解决问题.
小结:当已知条件中没有已知度数的角而又要求角的度数时,一般采用方程思想来解决问题. 设出要求的角的度数,然后根据等腰三角形的性质以及三角形外角与内角之间的关系,用含未知数的式子表示出一个三角形的三个内角的度数,再利用三角形的内角和等于180°列出方程,求出未知数的值即可.
【同步练习】
一、选择题
1.已知等腰三角形的一个角是100°,则它的顶角是( )
A.40° B.60° C.80° D.100°
2.【2021·赤峰】如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D的度数为( )
A.85° B.75° C.65° D.30°
第2题图 第5题图 第8题图
3.等腰三角形一边长等于5,另一边长等于9,则它的周长是( )
A.14 B.23 C.19 D.19或23
4.(2021济宁模拟)已知等腰三角形的周长为22,一边长为8,则它的底边长是( )
A.8 B.6 C.7或8 D.6或8
5.【2021·自贡】如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( )
A.72° B.36° C.74° D.88°
6.下列说法:①顶角相等的两个等腰三角形的底角一定相等;②底边相等的两个等腰三角形全等;③腰长相等且有一个角是20°的两个等腰三角形全等.其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.0个
7.等腰三角形腰上的高与底边的夹角α与顶角β之间的关系 ( )
A.α=β B.α=2β C.β=2α D.不能确定
8.如图,在△ABC中,AB=AC,AD⊥BC,有以下结论:
①△ABD≌△ACD;②D为边BC的中点;
③∠B=∠C;④AD是△ABC的一条角平分线.
其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
第9题图 第10题图 第11题图
10.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为 ( )
A.50° B.51° C.51.5° D.52.5°
11.如图,已知O是四边形ABCD内的点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的度数为( )
A.70° B.110° C.140° D.150°
二、填空题
12.等腰三角形的两个________相等(简写成“等边对等角”).注意:“等边对等角”是在__________三角形中.
13.等腰三角形的顶角________、底边上的______、底边上的______相互重合(简写成“__________”).
14.已知等腰三角形的一个外角为130°,则它的顶角的度数为 .
15.【2021·滨州】如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的大小为________.
第15题图 第16题图 第17题图
16.【2021·广州】如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B′,当B′D∥AC时,则∠BCD的度数为________.
17.【2021·鞍山】如图,∠POQ=90°,定长为a的线段端点A,B分别在射线OP,OQ上运动(点A,B不与点O重合),C为AB的中点,作△OAC关于直线OC对称的△OA′C,A′O交AB于点D,当△OBD是等腰三角形时,∠OBD的度数为________.
三、解答题
18.△ABC中,AD是BC边的中线,AD是BC边上的高,求证:AD是∠BAC的平分线.
19.如图,∠BAD=90°,AB=AC,AC的垂直平分线交BC于D,交AC于E.
(1)求∠BAC的度数;
(2)若AB=10,BC=17.32,求△ABD的周长.
20.如图,在△ABC中,AB=AC,AD是BC边上的中线,延长CB至点E,延长BC至点F,使BE=CF,连接AE,AF.
求证:AD平分∠EAF.
21.【2021·无锡】已知:如图,AC,DB相交于点O,AB=DC,∠ABO=∠DCO.求证:
(1)△ABO≌△DCO;
(2)∠OBC=∠OCB.
22.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
23.如图,△ABC中,AB=AC,D为BC边上的中点,DE⊥AB于E,DF⊥AC于F.
(1)求证:DE=DF;
(2)过B作BM⊥AC于M,D为BC的中点改为D在BC上(D不与B、C重合),其余条件不变,问DE、DF、BM的关系怎样?说明理由.
24.【2020·绍兴】问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】若某个等腰三角形的两边长分别为4和6,求这个等腰三角形的周长.
解题秘方:根据等腰三角形的定义确定腰和底边的长,再利用三角形三边关系进行判断并计算.
解:∵等腰三角形的底边长和腰长不确定,∴需分两种情况讨论. 第一种情况:当4 为腰长时,该等腰三角形的三边长分别为4,4,6,∵ 4+4>6,满足三角形的三边关系, ∴周长=4+4+6=14;第二种情况:当 6为腰长时,该等腰三角形的三边长分别为4,6,6,∵ 4+6>6,满足三角形的三边关系,∴周长=6+6+4=16.
综上可知,这个等腰三角形的周长为14或16.
特别提醒:等腰三角形的边分腰和底边,若没有说明,则必须分类讨论,同时注意三角形的三边关系.
【例2】如图,在△ABC中,AB=AC,AD平分∠BAC.
解题秘方:紧扣等腰三角形的性质进行解答.
(1)求∠ADB的度数;
解:∵ AB=AC,AD平分∠BAC,
∴ AD⊥BC,
∴∠ADB=90°.
(2)若∠BAC=100°,求∠B,∠C的度数;
解:在△ABC中,∵ AB=AC,∠BAC=100°,
∴∠B=∠C=×(180°-100°)=40°.
(3)若BC=3 cm,求BD的长.
解:∵ AB=AC,AD平分∠BAC,
∴ AD是BC边上的中线,
∴ BD=BC=×3=1.5(cm).
【例3】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高. 求证:BD=CE.
解题秘方:利用等腰三角形的边角性质为证明△BEC和△CDB全等创造条件.
证明:方法一 ∵ AB=AC,∴∠ABC=∠ACB.
∵ BD⊥AC,CE⊥AB,∴∠BDC=∠BEC=90°.
在△BEC和△CDB中,
∴△BEC≌△CDB(AAS). ∴ BD=CE.
方法二 ∵ S△ABC=AB·CE,S△ABC=AC·BD,AB=AC,∴ BD=CE.
【例4】如图,在△ABC中,AB=AC,点D,E分别在AC,AB边上,且BC=BD,AD=DE=EB,求∠A 的度数.
解题秘方:利用“等边对等角”及三角形外角的性质将△ABC中的三个角都用要求的∠A来表示,利用三角形内角和解决问题.
解:设∠A=x°,∵ AD=DE,∴∠AED=∠A=x°.
∵ DE=EB,∴∠EBD=∠BDE=x°,
∴∠BDC=∠A+∠EBD=x°.
∵ BC=BD,∴∠C=∠BDC=x°.
∵ AB=AC,∴∠ABC=∠C=x°.
∴ x+x+x=180,解得x=45. ∴∠A=45°.
小结:当已知条件中没有已知度数的角而又要求角的度数时,一般采用方程思想来解决问题. 设出要求的角的度数,然后根据等腰三角形的性质以及三角形外角与内角之间的关系,用含未知数的式子表示出一个三角形的三个内角的度数,再利用三角形的内角和等于180°列出方程,求出未知数的值即可.
【同步练习】
一、选择题
1.已知等腰三角形的一个角是100°,则它的顶角是( D )
A.40° B.60° C.80° D.100°
2.【2021·赤峰】如图,AB∥CD,点E在线段BC上,CD=CE,若∠ABC=30°,则∠D的度数为( B )
A.85° B.75° C.65° D.30°
第2题图 第5题图 第8题图
3.等腰三角形一边长等于5,另一边长等于9,则它的周长是( D )
A.14 B.23 C.19 D.19或23
4.(2021济宁模拟)已知等腰三角形的周长为22,一边长为8,则它的底边长是( D )
A.8 B.6 C.7或8 D.6或8
5.【2021·自贡】如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( A )
A.72° B.36° C.74° D.88°
6.下列说法:①顶角相等的两个等腰三角形的底角一定相等;②底边相等的两个等腰三角形全等;③腰长相等且有一个角是20°的两个等腰三角形全等.其中正确的个数有 ( A )
A.1个 B.2个 C.3个 D.0个
7.等腰三角形腰上的高与底边的夹角α与顶角β之间的关系 ( C )
A.α=β B.α=2β C.β=2α D.不能确定
8.如图,在△ABC中,AB=AC,AD⊥BC,有以下结论:
①△ABD≌△ACD;②D为边BC的中点;
③∠B=∠C;④AD是△ABC的一条角平分线.
其中,正确的有( D )
A.1个 B.2个 C.3个 D.4个
9.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是( B )
A.20° B.35° C.40° D.70°
第9题图 第10题图 第11题图
10.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为 ( D )
A.50° B.51° C.51.5° D.52.5°
11.如图,已知O是四边形ABCD内的点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的度数为( D )
A.70° B.110° C.140° D.150°
二、填空题
12.等腰三角形的两个________相等(简写成“等边对等角”).注意:“等边对等角”是在__________三角形中.
【答案】底角 同一个
13.等腰三角形的顶角________、底边上的______、底边上的______相互重合(简写成“__________”).
【答案】平分线 中线 高 三线合一
14.已知等腰三角形的一个外角为130°,则它的顶角的度数为 .
【答案】50°或80°
15.【2021·滨州】如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的大小为________.
【答案】34°
第15题图 第16题图 第17题图
16.【2021·广州】如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B′,当B′D∥AC时,则∠BCD的度数为________.
【解析】∵AC=BC,∴∠A=∠B=38°.
∵∠B′D∥AC,∴∠ADB′=∠A=38°.
∵点B关于直线CD的对称点为B′,
∴∠CDB′=∠CDB=(38°+180°)=109°,
∴∠BCD=180°-∠B-∠CDB=180°-38°-109°=33°.
【答案】33°
17.【2021·鞍山】如图,∠POQ=90°,定长为a的线段端点A,B分别在射线OP,OQ上运动(点A,B不与点O重合),C为AB的中点,作△OAC关于直线OC对称的△OA′C,A′O交AB于点D,当△OBD是等腰三角形时,∠OBD的度数为________.
【解析】作AE⊥OA交OC的延长线于点E.
∵AE⊥OA,∴∠OAE=90°.
又∵∠POQ=90°,∴∠OAE=∠POQ.∴AE∥OB.
∴∠OBC=∠CAE.
∵C为AB的中点,∴BC=AC.
又∵∠BCO=∠ACE,∴△BCO≌△ACE.
∴OC=CE,OB=EA.
在△BOA和△EAO中,OB=AE,OA=AO,∠BOA=∠EAO=90°,∴△BOA≌△EAO,∴AB=OE.
∴OC=AC=BC.∴∠COA=∠BAO,∠OBC=∠BOC.
又由折叠性质可得∠COA=∠COA′.
∴∠COA=∠COA′=∠BAO.
设∠COA=∠COA′=∠BAO=x,则∠BCO=2x,∠A′OB=90°-2x,∠OBD=90°-x,∠BDO=∠AOD+∠BAO=3x.
①当OB=OD时,∠OBD=∠BDO.∴90°-x=3x.
解得x=22.5°. ∴∠OBD=90°-22.5°=67.5°.
②当BD=OD时,∠OBD=∠A′OB.
∴90°-x=90°-2x,方程无解.∴此情况不存在.
③当OB=DB时,∠BDO=∠A′OB. ∴3x=90°-2x.
解得x=18°.∴∠OBD=90°-18°=72°.
综上,∠OBD的度数为67.5°或72°.
【答案】67.5°或72°
三、解答题
18.△ABC中,AD是BC边的中线,AD是BC边上的高,求证:AD是∠BAC的平分线.
证明:由题意得,∵AD⊥BC,BD=CD,
∴AD是BC的垂直平分线.
∴AB=AC.
∵AD是BC边的中线,
∴AD是∠BAC的平分线.
19.如图,∠BAD=90°,AB=AC,AC的垂直平分线交BC于D,交AC于E.
(1)求∠BAC的度数;
(2)若AB=10,BC=17.32,求△ABD的周长.
解:(1)∵AB=AC,∴∠B=∠C,
设∠B=∠C=x°,∵∠BAD=90°,
∴∠ADB=90°-∠B=(90-x)°.
∵DE垂直平分AC,∴DA=DC,
∴∠DAC=∠C=x°,∴90-x=2x,
解得x=30,∴∠BAC=90°+30°=120°.
(2)由(1)知DA=DC,
∴△ABD的周长=AB+AD+BD=AB+BC=10+17.32=27.32.
20.如图,在△ABC中,AB=AC,AD是BC边上的中线,延长CB至点E,延长BC至点F,使BE=CF,连接AE,AF.
求证:AD平分∠EAF.
证明:∵在△ABC中,AB=AC,AD是BC边上的中线,
∴AD平分∠BAC,∠ABD=∠ACD.
∴∠BAD=∠CAD,∠ABE=∠ACF.
在△ABE和△ACF中,
∴△ABE≌△ACF(SAS).∴∠BAE=∠CAF.
∴∠BAE+∠BAD=∠CAF+∠CAD,
即∠EAD=∠FAD.∴AD平分∠EAF.
21.【2021·无锡】已知:如图,AC,DB相交于点O,AB=DC,∠ABO=∠DCO.求证:
(1)△ABO≌△DCO;
证明:在△ABO和△DCO中,
∴△ABO≌△DCO(AAS).
(2)∠OBC=∠OCB.
证明:由(1)知,△ABO≌△DCO,
∴OB=OC.∴∠OBC=∠OCB.
22.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
证明:∵∠CAF=∠BAE,∴∠EAF=∠BAC.
又∵AE=AB,AF=AC,
∴△EAF≌△BAC(SAS).∴EF=BC.
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
解:∵AB=AE,∠ABC=65°,
∴∠BAE=180°-65°×2=50°.
∵∠CAF=∠BAE,∴∠FAG=50°.
∵△EAF≌△BAC,∴∠F=∠ACB=28°.
∴∠FGC=∠FAG+∠F=50°+28°=78°.
23.如图,△ABC中,AB=AC,D为BC边上的中点,DE⊥AB于E,DF⊥AC于F.
(1)求证:DE=DF;
(2)过B作BM⊥AC于M,D为BC的中点改为D在BC上(D不与B、C重合),其余条件不变,问DE、DF、BM的关系怎样?说明理由.
(1)证明:连接AD,∵AB=AC,D是BC的中点,∴AD平分∠BAC,∵DE⊥AB,DF⊥AC,∴DE=DF;
(2)解:BM=DE+DF.理由:连接AD,∵S△ABD=AB·DE,S△ADC=AC·DF,S△ABC=BM·AC,∵S△ABD+S△ADC=S△ABC,∴AB·DE+AC·DF=BM·AC,∵AB=AC,∴DE+DF=BM.
24.【2020·绍兴】问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
解:∠DAC的度数不会改变.
理由如下:∵EA=EC,∴∠CAE=∠C.∴∠AED=2∠C.
∵∠BAE=90°,BA=BD,
∴∠BAD= (180°-∠B)= [180°-(90°-2∠C)]=45°+∠C.
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.
∴∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
解:设∠B=m°.∵BA=BD,
∴∠BAD= (180°-m°)=90°-m°.
∴∠DAE=∠BAE-∠BAD=n°-90°+m°.
∵EA=EC,∴∠EAC=∠C.∴∠AEB=2∠CAE.
∵∠AEB=180°-n°-m°,
∴∠CAE=∠AEB=90°-n°-m°.
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
