13.3.1.2 等腰三角形的判定同步练习 (含答案)
文档属性
| 名称 | 13.3.1.2 等腰三角形的判定同步练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 19:49:21 | ||
图片预览


文档简介
13.3.1等腰三角形
第2课时 等腰三角形的判定
【知识重点】
知识点1 等腰三角形的判定
1. 判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
几何语言:如图,在△ABC中,
∵∠B=∠C,
∴ AB=AC.
2. 等腰三角形的性质与判定的异同
相同点:使用的前提都是“在同一个三角形中”.
不同点:等腰三角形的性质:两边相等→这两边所对的角相等.
等腰三角形的判定:两角相等→这两角所对的边相等.
特别提醒
●等腰三角形的定义也是一种判定方法.
●“等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角的关系得到角相等,从而得到所对的边相等.
【经典例题】
【例1】如图,在△ABC中,P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA
的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由.
解题秘方:利用“等角对等边”判定等腰三角形,只需证明三角形两个内角相等即可.
总结:根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,可以证明这个三角形有两个内角相等,所以证明两个内角相等是判定等腰三角形的关键所在.
【同步练习】
一、选择题
1.在△ABC中,其两个内角的度数如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
2.下列可以确定△ABC是等腰三角形的是( )
A.AB=AC B.∠A=∠B
C.∠A∶∠B∶∠C=2∶3∶2 D.以上都可以
3.在△ABC中,∠A=45°,∠B=45°,则下列判断错误的是( )
A.△ABC是直角三角形 B.△ABC是锐角三角形
C.△ABC是等腰三角形 D.∠A和∠B互余
4.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A.①②④ B.②③④ C.①②③ D.①③④
5.下列能断定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60° B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4 D.AB=3,BC=7,周长为13
6.如图,在△ABC中,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中的等腰三角形有( )
A.6个 B.5个 C.4个 D.3个
第6题图 第7题图 第8题图
7.如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中等腰三角形共有( )
A.4个 B.5个 C.6个 D.2个
8.【2021·扬州】如图,在4×4的正方形网格中有两个格点A,B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,满足条件的格点C的个数是( )
A.2 B.3 C.4 D.5
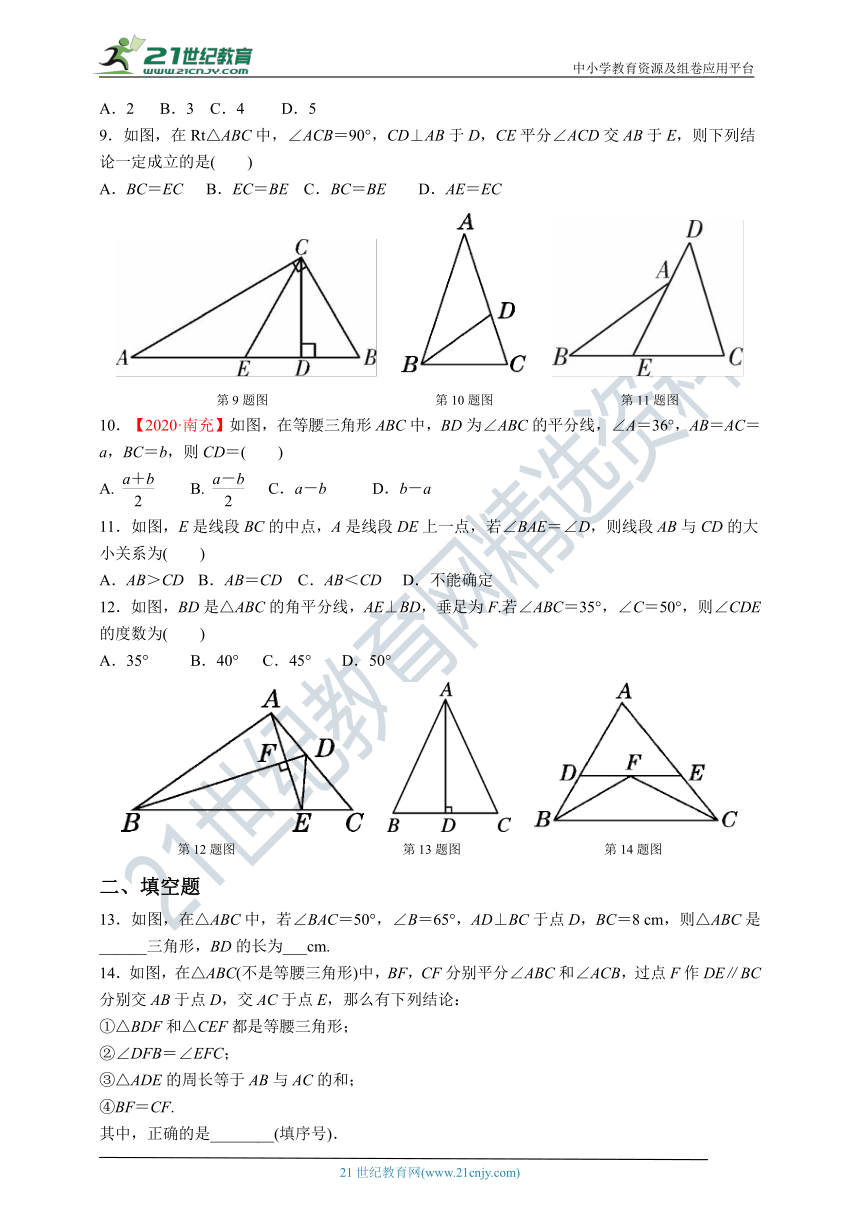
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=EC B.EC=BE C.BC=BE D.AE=EC
第9题图 第10题图 第11题图
10.【2020·南充】如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( )
A. B. C.a-b D.b-a
11.如图,E是线段BC的中点,A是线段DE上一点,若∠BAE=∠D,则线段AB与CD的大小关系为( )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
12.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
第12题图 第13题图 第14题图
二、填空题
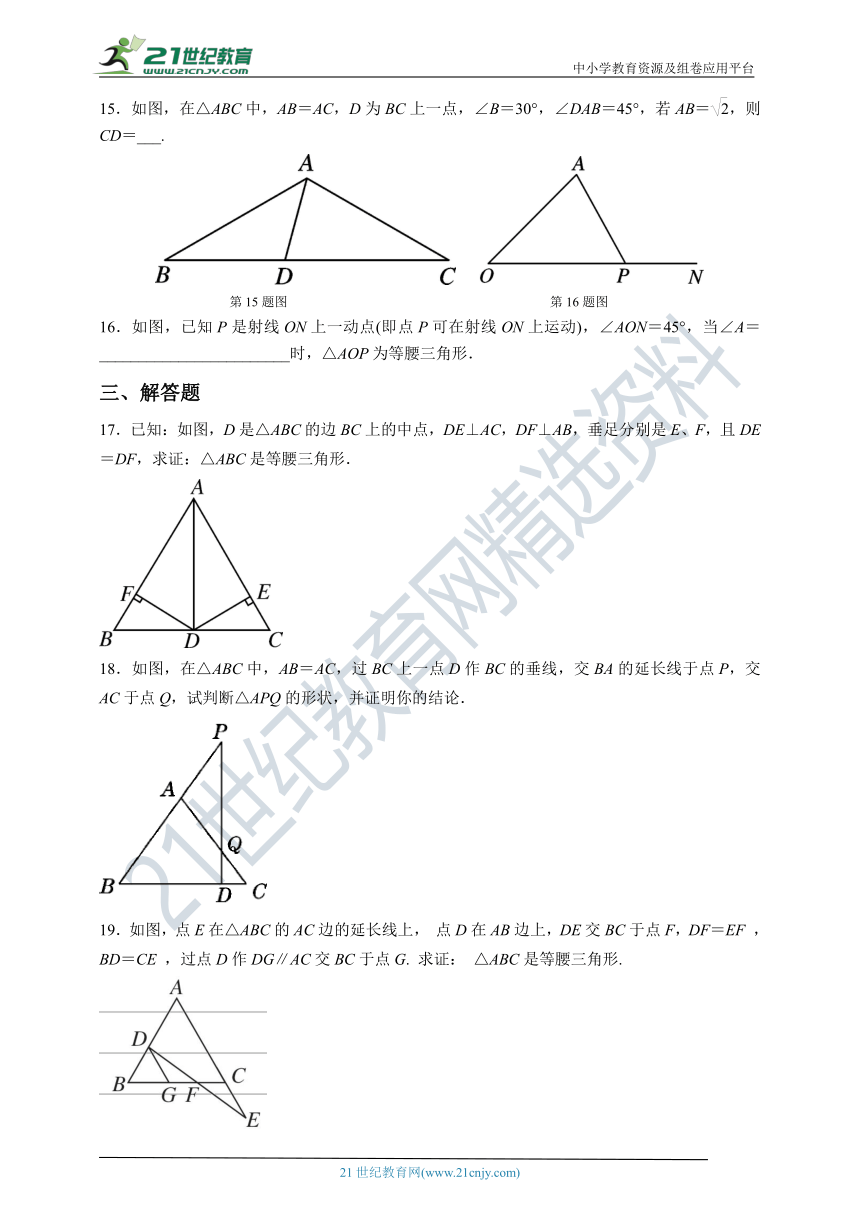
13.如图,在△ABC中,若∠BAC=50°,∠B=65°,AD⊥BC于点D,BC=8 cm,则△ABC是______三角形,BD的长为___cm.
14.如图,在△ABC(不是等腰三角形)中,BF,CF分别平分∠ABC和∠ACB,过点F作DE∥BC分别交AB于点D,交AC于点E,那么有下列结论:
①△BDF和△CEF都是等腰三角形;
②∠DFB=∠EFC;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中,正确的是________(填序号).
15.如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,∠DAB=45°,若AB=,则CD=___.
第15题图 第16题图
16.如图,已知P是射线ON上一动点(即点P可在射线ON上运动),∠AON=45°,当∠A=________________________时,△AOP为等腰三角形.
三、解答题
17.已知:如图,D是△ABC的边BC上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且DE=DF,求证:△ABC是等腰三角形.
18.如图,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P,交AC于点Q,试判断△APQ的形状,并证明你的结论.
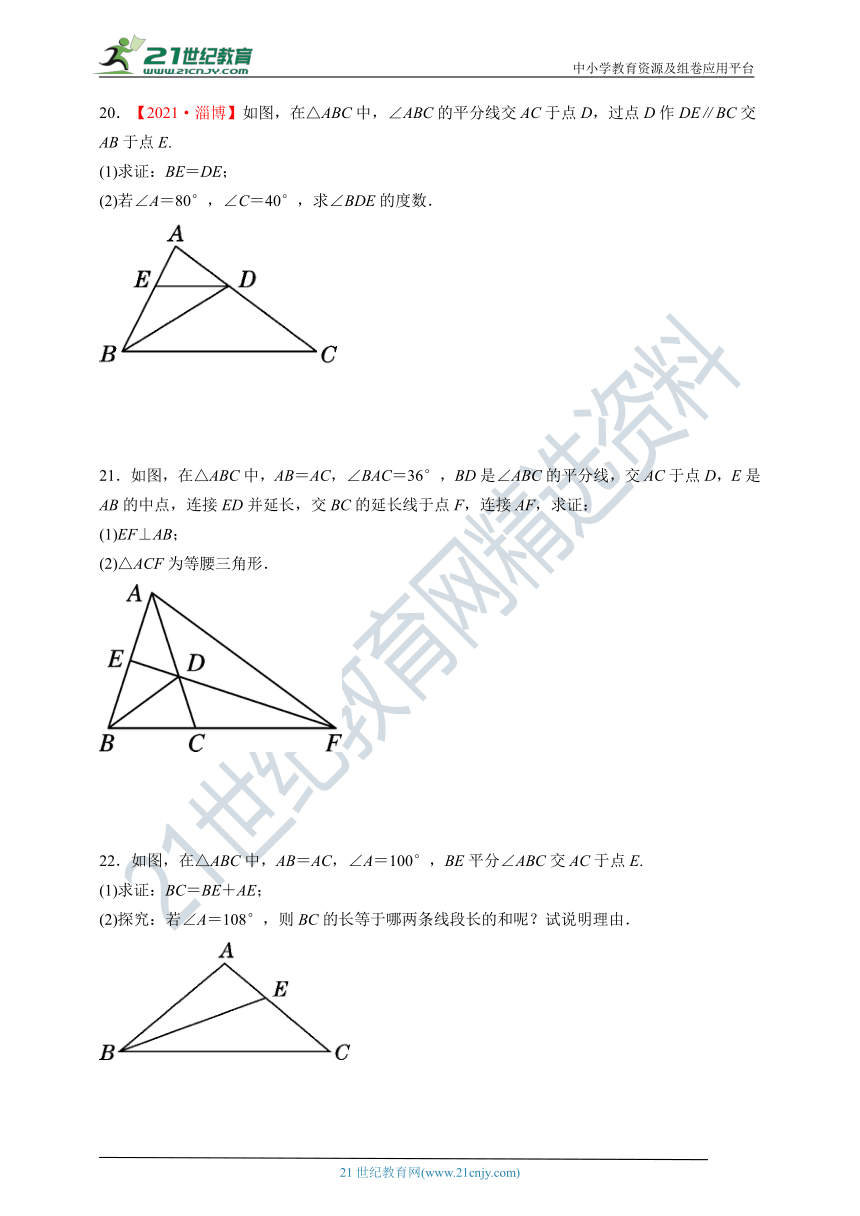
19.如图,点E在△ABC的AC边的延长线上, 点D在AB边上,DE交BC于点F,DF=EF ,BD=CE ,过点D作DG∥AC交BC于点G. 求证: △ABC是等腰三角形.
20.【2021·淄博】如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
21.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
22.如图,在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
(1)求证:BC=BE+AE;
(2)探究:若∠A=108°,则BC的长等于哪两条线段长的和呢?试说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,在△ABC中,P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA
的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由.
解题秘方:利用“等角对等边”判定等腰三角形,只需证明三角形两个内角相等即可.
解:△ABC是等腰三角形. 理由如下:
∵ AQ=AR,∴∠R=∠AQR.
又∵∠BQP=∠AQR,∴∠R=∠BQP.
∵ RP⊥BC,∴∠RPB=∠RPC=90°.
∴∠B+∠BQP=90°,∠C+∠R=90°,
∴∠B=∠C, ∴ AB=AC. ∴△ABC是等腰三角形.
总结:根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,可以证明这个三角形有两个内角相等,所以证明两个内角相等是判定等腰三角形的关键所在.
【同步练习】
一、选择题
1.在△ABC中,其两个内角的度数如下,则能判定△ABC为等腰三角形的是( C )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
2.下列可以确定△ABC是等腰三角形的是( D )
A.AB=AC B.∠A=∠B
C.∠A∶∠B∶∠C=2∶3∶2 D.以上都可以
3.在△ABC中,∠A=45°,∠B=45°,则下列判断错误的是( B )
A.△ABC是直角三角形 B.△ABC是锐角三角形
C.△ABC是等腰三角形 D.∠A和∠B互余
4.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( D )
A.①②④ B.②③④ C.①②③ D.①③④
5.下列能断定△ABC为等腰三角形的是( B )
A.∠A=30°,∠B=60° B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4 D.AB=3,BC=7,周长为13
6.如图,在△ABC中,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中的等腰三角形有( B )
A.6个 B.5个 C.4个 D.3个
第6题图 第7题图 第8题图
7.如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中等腰三角形共有( C )
A.4个 B.5个 C.6个 D.2个
8.【2021·扬州】如图,在4×4的正方形网格中有两个格点A,B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,满足条件的格点C的个数是( B )
A.2 B.3 C.4 D.5
【解析】分情况讨论:
①AB为等腰直角三角形ABC的底边时,符合条件的C点有0个;
②AB为等腰直角三角形ABC其中的一条腰时,符合条件的C点有3个.
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( C )
A.BC=EC B.EC=BE C.BC=BE D.AE=EC
第9题图 第10题图 第11题图
10.【2020·南充】如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( C )
A. B. C.a-b D.b-a
11.如图,E是线段BC的中点,A是线段DE上一点,若∠BAE=∠D,则线段AB与CD的大小关系为( B )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
【提示】延长AE至F,使EF=AE,连CF.
12.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( C )
A.35° B.40° C.45° D.50°
【解析】根据角平分线的定义和垂直的定义得到∠ABD=∠EBD,∠AFB=∠EFB=90°,∴∠BAF=∠BEF.
∴AB=BE. 根据等腰三角形的性质得到AF=EF,
由线段垂直平分线的性质得AD=ED,
∴∠DAF=∠DEF.∴∠BAD=∠BED.
∵∠BAD=180°-35°-50°=95°,∠BED=∠CDE+50°,∴∠CDE=95°-50°=45°.
第12题图 第13题图 第14题图
二、填空题
13.如图,在△ABC中,若∠BAC=50°,∠B=65°,AD⊥BC于点D,BC=8 cm,则△ABC是______三角形,BD的长为___cm.
【答案】等腰 4
14.如图,在△ABC(不是等腰三角形)中,BF,CF分别平分∠ABC和∠ACB,过点F作DE∥BC分别交AB于点D,交AC于点E,那么有下列结论:
①△BDF和△CEF都是等腰三角形;
②∠DFB=∠EFC;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中,正确的是________(填序号).
【答案】①③
15.如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,∠DAB=45°,若AB=,则CD=___.
【答案】
第15题图 第16题图
16.如图,已知P是射线ON上一动点(即点P可在射线ON上运动),∠AON=45°,当∠A=________________________时,△AOP为等腰三角形.
【答案】45°或67.5°或90°
三、解答题
17.已知:如图,D是△ABC的边BC上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且DE=DF,求证:△ABC是等腰三角形.
证明:∵DE⊥AC,DF⊥AB,∴∠DEC=∠DFB=90°.在Rt△DEC和Rt△DFB中,,∴Rt△DEC≌Rt△DFB(HL).∴∠C=∠B,∴AB=AC(等角对等边),∴△ABC是等腰三角形.
18.如图,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P,交AC于点Q,试判断△APQ的形状,并证明你的结论.
解:△APQ是等腰三角形.证明如下:
∵AB=AC,∴∠B=∠C.
∵PD⊥BC,∴∠BDP=∠PDC=90°.
∴∠P+∠B=90°,∠DQC+∠C=90°.
∵∠B=∠C,∴∠P=∠DQC.
∵∠DQC=∠AQP,∴∠AQP=∠P.
∴△APQ为等腰三角形.
19.如图,点E在△ABC的AC边的延长线上, 点D在AB边上,DE交BC于点F,DF=EF ,BD=CE ,过点D作DG∥AC交BC于点G. 求证: △ABC是等腰三角形.
证明:∵DG∥AC,∴∠DGB=∠ACB,∠DGF=∠ECF.
又∵∠DFG=∠EFC,DF=EF,
∴△GDF≌△CEF, ∴DG=EC.
∵BD=CE,∴BD=DG,∴∠DGB=∠B.
∵∠DGB=∠ACB,∴∠B=∠ACB.
∴AB=AC,即△ABC是等腰三角形.
20.【2021·淄博】如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
证明:∵在△ABC中,∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD.
∵DE∥BC,∴∠EDB=∠CBD.
∴∠EBD=∠EDB.∴BE=DE.
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
解:∵∠A=80°,∠C=40°,∴∠ABC=60°.
∵∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD=∠ABC=30°.
由(1)知∠BDE=∠CBD,∴∠BDE=30°.
21.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
证明:(1)∵AB=AC,
∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵BD是∠ABC的平分线,
∴∠ABD=∠FBD=36°,
∴∠BAD=∠ABD,∴AD=BD.
又∵E是AB的中点,∴DE⊥AB,即EF⊥AB.
(2)∵EF⊥AB,AE=BE,∴FE垂直平分AB,
∴AF=BF,∴∠BAF=∠ABF.
∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,
∴∠AFC=∠ACB-∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
22.如图,在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
(1)求证:BC=BE+AE;
证明:在BC上截取BD=BE,连接DE,如图所示.
∵AB=AC,∠BAC=100°,
∴∠ABC=∠C=(180°-100°)÷2=40°.
∵BE平分∠ABC,∴∠CBE=∠ABE=20°.
∵BD=BE,∴∠BDE=∠BED=(180°-20°)÷2=80°.
又∵∠BDE=∠C+∠CED,∠C=40°,
∴∠CED=40°=∠C.∴DE=DC.
过点E作EM⊥BA交BA的延长线于点M,EN⊥BC于点N.
∵BE平分∠ABC,EM⊥BA,EN⊥BC,∴EM=EN.
∵∠BAC=100°,∴∠EAM=180°-100°=80°.
在△EMA和△END中,
∴△EMA≌△END(AAS).∴EA=ED.
又∵DE=DC,∴EA=DC. ∴BC=BD+DC=BE+AE.
(2)探究:若∠A=108°,则BC的长等于哪两条线段长的和呢?试说明理由.
解:BC=CE+AB.理由如下:
在CB上截取CP=CE,连接PE,如图所示.
∵AB=AC,∠A=108°,
∴∠ABC=∠C=(180°-108°)÷2=36°.
∵CP=CE,∴∠CPE=(180°-36°)÷2=72°.
∴∠BPE=180°-72°=108°.
∴∠BPE=∠A.
∵BE平分∠ABC,∴∠ABE=∠PBE.
在△ABE和△PBE中,
∴△ABE≌△PBE(AAS).∴BA=BP.
∴BC=CP+BP=CE+AB.
第2课时 等腰三角形的判定
【知识重点】
知识点1 等腰三角形的判定
1. 判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
几何语言:如图,在△ABC中,
∵∠B=∠C,
∴ AB=AC.
2. 等腰三角形的性质与判定的异同
相同点:使用的前提都是“在同一个三角形中”.
不同点:等腰三角形的性质:两边相等→这两边所对的角相等.
等腰三角形的判定:两角相等→这两角所对的边相等.
特别提醒
●等腰三角形的定义也是一种判定方法.
●“等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角的关系得到角相等,从而得到所对的边相等.
【经典例题】
【例1】如图,在△ABC中,P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA
的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由.
解题秘方:利用“等角对等边”判定等腰三角形,只需证明三角形两个内角相等即可.
总结:根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,可以证明这个三角形有两个内角相等,所以证明两个内角相等是判定等腰三角形的关键所在.
【同步练习】
一、选择题
1.在△ABC中,其两个内角的度数如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
2.下列可以确定△ABC是等腰三角形的是( )
A.AB=AC B.∠A=∠B
C.∠A∶∠B∶∠C=2∶3∶2 D.以上都可以
3.在△ABC中,∠A=45°,∠B=45°,则下列判断错误的是( )
A.△ABC是直角三角形 B.△ABC是锐角三角形
C.△ABC是等腰三角形 D.∠A和∠B互余
4.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A.①②④ B.②③④ C.①②③ D.①③④
5.下列能断定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60° B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4 D.AB=3,BC=7,周长为13
6.如图,在△ABC中,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中的等腰三角形有( )
A.6个 B.5个 C.4个 D.3个
第6题图 第7题图 第8题图
7.如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中等腰三角形共有( )
A.4个 B.5个 C.6个 D.2个
8.【2021·扬州】如图,在4×4的正方形网格中有两个格点A,B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,满足条件的格点C的个数是( )
A.2 B.3 C.4 D.5
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=EC B.EC=BE C.BC=BE D.AE=EC
第9题图 第10题图 第11题图
10.【2020·南充】如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( )
A. B. C.a-b D.b-a
11.如图,E是线段BC的中点,A是线段DE上一点,若∠BAE=∠D,则线段AB与CD的大小关系为( )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
12.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A.35° B.40° C.45° D.50°
第12题图 第13题图 第14题图
二、填空题
13.如图,在△ABC中,若∠BAC=50°,∠B=65°,AD⊥BC于点D,BC=8 cm,则△ABC是______三角形,BD的长为___cm.
14.如图,在△ABC(不是等腰三角形)中,BF,CF分别平分∠ABC和∠ACB,过点F作DE∥BC分别交AB于点D,交AC于点E,那么有下列结论:
①△BDF和△CEF都是等腰三角形;
②∠DFB=∠EFC;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中,正确的是________(填序号).
15.如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,∠DAB=45°,若AB=,则CD=___.
第15题图 第16题图
16.如图,已知P是射线ON上一动点(即点P可在射线ON上运动),∠AON=45°,当∠A=________________________时,△AOP为等腰三角形.
三、解答题
17.已知:如图,D是△ABC的边BC上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且DE=DF,求证:△ABC是等腰三角形.
18.如图,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P,交AC于点Q,试判断△APQ的形状,并证明你的结论.
19.如图,点E在△ABC的AC边的延长线上, 点D在AB边上,DE交BC于点F,DF=EF ,BD=CE ,过点D作DG∥AC交BC于点G. 求证: △ABC是等腰三角形.
20.【2021·淄博】如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
21.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
22.如图,在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
(1)求证:BC=BE+AE;
(2)探究:若∠A=108°,则BC的长等于哪两条线段长的和呢?试说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,在△ABC中,P是BC边上一点,过点P作BC的垂线,交AB于点Q,交CA
的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由.
解题秘方:利用“等角对等边”判定等腰三角形,只需证明三角形两个内角相等即可.
解:△ABC是等腰三角形. 理由如下:
∵ AQ=AR,∴∠R=∠AQR.
又∵∠BQP=∠AQR,∴∠R=∠BQP.
∵ RP⊥BC,∴∠RPB=∠RPC=90°.
∴∠B+∠BQP=90°,∠C+∠R=90°,
∴∠B=∠C, ∴ AB=AC. ∴△ABC是等腰三角形.
总结:根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,可以证明这个三角形有两个内角相等,所以证明两个内角相等是判定等腰三角形的关键所在.
【同步练习】
一、选择题
1.在△ABC中,其两个内角的度数如下,则能判定△ABC为等腰三角形的是( C )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
2.下列可以确定△ABC是等腰三角形的是( D )
A.AB=AC B.∠A=∠B
C.∠A∶∠B∶∠C=2∶3∶2 D.以上都可以
3.在△ABC中,∠A=45°,∠B=45°,则下列判断错误的是( B )
A.△ABC是直角三角形 B.△ABC是锐角三角形
C.△ABC是等腰三角形 D.∠A和∠B互余
4.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( D )
A.①②④ B.②③④ C.①②③ D.①③④
5.下列能断定△ABC为等腰三角形的是( B )
A.∠A=30°,∠B=60° B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4 D.AB=3,BC=7,周长为13
6.如图,在△ABC中,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中的等腰三角形有( B )
A.6个 B.5个 C.4个 D.3个
第6题图 第7题图 第8题图
7.如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中等腰三角形共有( C )
A.4个 B.5个 C.6个 D.2个
8.【2021·扬州】如图,在4×4的正方形网格中有两个格点A,B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,满足条件的格点C的个数是( B )
A.2 B.3 C.4 D.5
【解析】分情况讨论:
①AB为等腰直角三角形ABC的底边时,符合条件的C点有0个;
②AB为等腰直角三角形ABC其中的一条腰时,符合条件的C点有3个.
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( C )
A.BC=EC B.EC=BE C.BC=BE D.AE=EC
第9题图 第10题图 第11题图
10.【2020·南充】如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( C )
A. B. C.a-b D.b-a
11.如图,E是线段BC的中点,A是线段DE上一点,若∠BAE=∠D,则线段AB与CD的大小关系为( B )
A.AB>CD B.AB=CD C.AB<CD D.不能确定
【提示】延长AE至F,使EF=AE,连CF.
12.如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( C )
A.35° B.40° C.45° D.50°
【解析】根据角平分线的定义和垂直的定义得到∠ABD=∠EBD,∠AFB=∠EFB=90°,∴∠BAF=∠BEF.
∴AB=BE. 根据等腰三角形的性质得到AF=EF,
由线段垂直平分线的性质得AD=ED,
∴∠DAF=∠DEF.∴∠BAD=∠BED.
∵∠BAD=180°-35°-50°=95°,∠BED=∠CDE+50°,∴∠CDE=95°-50°=45°.
第12题图 第13题图 第14题图
二、填空题
13.如图,在△ABC中,若∠BAC=50°,∠B=65°,AD⊥BC于点D,BC=8 cm,则△ABC是______三角形,BD的长为___cm.
【答案】等腰 4
14.如图,在△ABC(不是等腰三角形)中,BF,CF分别平分∠ABC和∠ACB,过点F作DE∥BC分别交AB于点D,交AC于点E,那么有下列结论:
①△BDF和△CEF都是等腰三角形;
②∠DFB=∠EFC;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中,正确的是________(填序号).
【答案】①③
15.如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,∠DAB=45°,若AB=,则CD=___.
【答案】
第15题图 第16题图
16.如图,已知P是射线ON上一动点(即点P可在射线ON上运动),∠AON=45°,当∠A=________________________时,△AOP为等腰三角形.
【答案】45°或67.5°或90°
三、解答题
17.已知:如图,D是△ABC的边BC上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且DE=DF,求证:△ABC是等腰三角形.
证明:∵DE⊥AC,DF⊥AB,∴∠DEC=∠DFB=90°.在Rt△DEC和Rt△DFB中,,∴Rt△DEC≌Rt△DFB(HL).∴∠C=∠B,∴AB=AC(等角对等边),∴△ABC是等腰三角形.
18.如图,在△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA的延长线于点P,交AC于点Q,试判断△APQ的形状,并证明你的结论.
解:△APQ是等腰三角形.证明如下:
∵AB=AC,∴∠B=∠C.
∵PD⊥BC,∴∠BDP=∠PDC=90°.
∴∠P+∠B=90°,∠DQC+∠C=90°.
∵∠B=∠C,∴∠P=∠DQC.
∵∠DQC=∠AQP,∴∠AQP=∠P.
∴△APQ为等腰三角形.
19.如图,点E在△ABC的AC边的延长线上, 点D在AB边上,DE交BC于点F,DF=EF ,BD=CE ,过点D作DG∥AC交BC于点G. 求证: △ABC是等腰三角形.
证明:∵DG∥AC,∴∠DGB=∠ACB,∠DGF=∠ECF.
又∵∠DFG=∠EFC,DF=EF,
∴△GDF≌△CEF, ∴DG=EC.
∵BD=CE,∴BD=DG,∴∠DGB=∠B.
∵∠DGB=∠ACB,∴∠B=∠ACB.
∴AB=AC,即△ABC是等腰三角形.
20.【2021·淄博】如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
证明:∵在△ABC中,∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD.
∵DE∥BC,∴∠EDB=∠CBD.
∴∠EBD=∠EDB.∴BE=DE.
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
解:∵∠A=80°,∠C=40°,∴∠ABC=60°.
∵∠ABC的平分线交AC于点D,
∴∠ABD=∠CBD=∠ABC=30°.
由(1)知∠BDE=∠CBD,∴∠BDE=30°.
21.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
证明:(1)∵AB=AC,
∠BAC=36°,
∴∠ABC=∠ACB=72°.
又∵BD是∠ABC的平分线,
∴∠ABD=∠FBD=36°,
∴∠BAD=∠ABD,∴AD=BD.
又∵E是AB的中点,∴DE⊥AB,即EF⊥AB.
(2)∵EF⊥AB,AE=BE,∴FE垂直平分AB,
∴AF=BF,∴∠BAF=∠ABF.
∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°.
又∵∠ACB=72°,
∴∠AFC=∠ACB-∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
22.如图,在△ABC中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.
(1)求证:BC=BE+AE;
证明:在BC上截取BD=BE,连接DE,如图所示.
∵AB=AC,∠BAC=100°,
∴∠ABC=∠C=(180°-100°)÷2=40°.
∵BE平分∠ABC,∴∠CBE=∠ABE=20°.
∵BD=BE,∴∠BDE=∠BED=(180°-20°)÷2=80°.
又∵∠BDE=∠C+∠CED,∠C=40°,
∴∠CED=40°=∠C.∴DE=DC.
过点E作EM⊥BA交BA的延长线于点M,EN⊥BC于点N.
∵BE平分∠ABC,EM⊥BA,EN⊥BC,∴EM=EN.
∵∠BAC=100°,∴∠EAM=180°-100°=80°.
在△EMA和△END中,
∴△EMA≌△END(AAS).∴EA=ED.
又∵DE=DC,∴EA=DC. ∴BC=BD+DC=BE+AE.
(2)探究:若∠A=108°,则BC的长等于哪两条线段长的和呢?试说明理由.
解:BC=CE+AB.理由如下:
在CB上截取CP=CE,连接PE,如图所示.
∵AB=AC,∠A=108°,
∴∠ABC=∠C=(180°-108°)÷2=36°.
∵CP=CE,∴∠CPE=(180°-36°)÷2=72°.
∴∠BPE=180°-72°=108°.
∴∠BPE=∠A.
∵BE平分∠ABC,∴∠ABE=∠PBE.
在△ABE和△PBE中,
∴△ABE≌△PBE(AAS).∴BA=BP.
∴BC=CP+BP=CE+AB.
