13.3.2.1 等边三角形的性质和判定同步练习 (含答案)
文档属性
| 名称 | 13.3.2.1 等边三角形的性质和判定同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 19:50:33 | ||
图片预览




文档简介
13.3.2等边三角形
第1课时 等边三角形的性质和判定
【知识重点】
知识点1 等边三角形的定义及性质
1. 定义 三边都相等的三角形叫做等边三角形,也叫正三角形.
2. 性质
(1)等边三角形的三条边都相等.
(2)等边三角形的三个内角都相等,并且每一个角都等于60°.
(3)等边三角形是轴对称图形,它有3 条对称轴,分别为三边的垂直平分线.
(4)各边上的高、中线、对角的角平分线重合,且长度相等.
特别解读
等边三角形是特殊的等腰三角形,具备等腰三角形的所有性质:
(1)任意两边都可以作为腰.
(2)任意一个角都可以作为顶角.
(3)任意一边上的“三线合一”.
知识点2 等边三角形的判定
1. 判定定理1 三个角都相等的三角形是等边三角形.
几何语言:如图,在△ABC中,
∵∠A=∠B=∠C,
∴△ABC是等边三角形.
2. 判定定理2 有一个角是60°的等腰三角形是等边三角形.
几何语言:如图,在△ ABC 中,
∵ AB=AC,∠A=60°或∠B=60°
或∠C=60°,
∴△ABC是等边三角形.
证明等边三角形的思维导图:
特别解读
1. 在等腰三角形中,只要有一个角是60°,无论这个角是顶角还是底角,判定定理2都成立.
2. 等边三角形的判定方法:
(1) 若已知三边关系,一般选用定义判定;
(2) 若已知三角关系,一般选用判定定理1判定;
(3) 若已知该三角形是等腰三角形,一般选用判定定理2判定.
【经典例题】
【例1】如图, △ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点, 且DE⊥AC,EF⊥BC, DF⊥AB,计算△DEF各个内角的度数.
解题秘方:紧扣等边三角形的三个内角都等于60°,求角的度数.
【例2】如图,等边三角形ABC的边长为3,D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化.
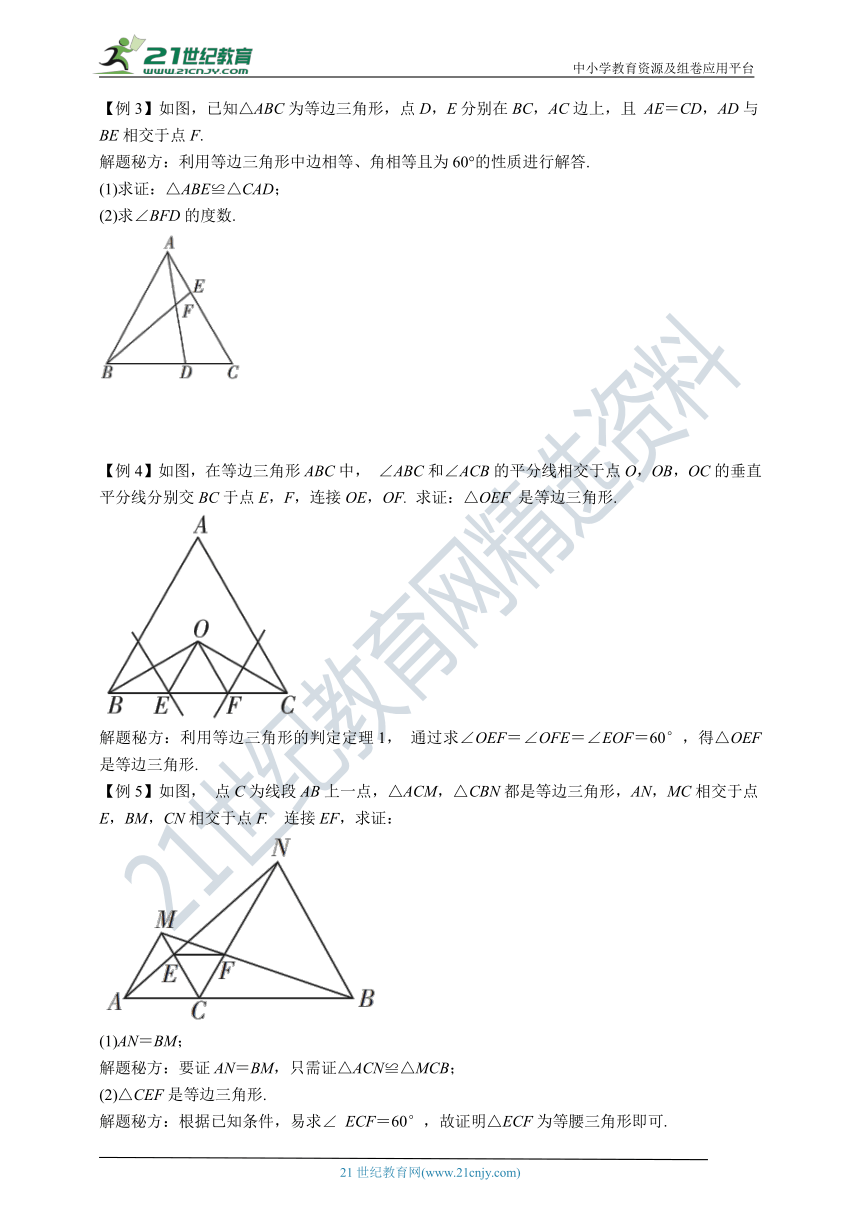
【例3】如图,已知△ABC为等边三角形,点D,E分别在BC,AC边上,且 AE=CD,AD与BE相交于点F.
解题秘方:利用等边三角形中边相等、角相等且为60°的性质进行解答.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
【例4】如图,在等边三角形ABC中, ∠ABC和∠ACB的平分线相交于点O,OB,OC的垂直平分线分别交BC于点E,F,连接OE,OF. 求证:△OEF 是等边三角形.
解题秘方:利用等边三角形的判定定理1, 通过求∠OEF=∠OFE=∠EOF=60°,得△OEF是等边三角形.
【例5】如图, 点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN,MC相交于点E,BM,CN相交于点F. 连接EF,求证:
(1)AN=BM;
解题秘方:要证AN=BM,只需证△ACN≌△MCB;
(2)△CEF是等边三角形.
解题秘方:根据已知条件,易求∠ ECF=60°,故证明△ECF为等腰三角形即可.
【同步练习】
一、选择题
1.下列性质中,等边三角形具有且等腰三角形也具有的是( )
A.三条边相等 B.三个内角相等
C.有三条对称轴 D.是轴对称图形
2.如图,一张等边三角形纸片,剪去一个角后得到一张四边形纸片,则图中∠α+∠β的度数是( )
A. 180° B. 220° C. 240° D. 300°
第2题图 第4题图 第5题图
3.关于等边三角形的说法:①等边三角形有三条对称轴;②有一个角等于60°的等腰三角形是等边三角形;③有两个角等于60°的三角形是等边三角形;④有两个角相等的等腰三角形是等边三角形.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
5.【2021·益阳】如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
6.【2021·福建】如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于( )
A.108° B.120° C.126° D.132°
第6题图 第7题图 第8题图
7.如图,等边三角形ABC的边长为2,CD平分∠ACB,交AB于点D,DE∥BC,则△ADE的周长为( )
A.2 B.2.5 C.3 D.4
8.如图,D,E,F分别是等边三角形ABC各边上的点,且AD=BE=CF,则△DEF的形状是( )
A.等边三角形 B.腰和底边不相等的等腰三角形
C.直角三角形 D.不等边三角形
9.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为( )
A.1.6 B.1.8 C.2 D.2.6
第9题图 第10题图 第11题图
10.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( )
A.9 B.8 C.6 D.7
11.如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连接BE,AD,M,N分别是线段BE,AD上的两点,且BM=BE,AN=AD,则△CMN的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
二、填空题
12.等边三角形的三个内角都________,并且每一个角都等于________.
13.三个角都________的三角形是等边三角形;有一个角是________的等腰三角形是等边三角形.
14.如图,在等边三角形ABC中,AD⊥BC,AB=5 cm,则DC的长为________________.
第14题图 第15题图 第16题图
15.已知D,E分别是等边三角形ABC中AB,AC上的点,且AE=BD,则BE与CD的夹角是_______________.
16.如图,△ABC中,∠ACB=90°,AC=BC,D为AB边上一点,且∠ADC=60°,沿CD翻折△CBD,点B落在点B′的位置,连接AB′,则B′A∶AC的值为 .
17.如图,在△ABC中,AB=BC=4,∠ACB=60°,BD是∠ABC的平分线,若M, N分别是BD和BC上的动点,当CM+MN取最小值时,BN的值是___.
三、解答题
18.如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为边作等边三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
19.如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
20.如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程.
21.(1)如图①,在等边三角形ABC中,M是BC上的任意一点(不含端点B,C),连接AM,以AM为边作等边三角形AMN,连接CN.求证:∠ABC=∠ACN;
(2)如图②,在等边三角形ABC中,M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中的结论∠ABC=∠ACN还成立吗?请说明理由.
22.如图,在等边三角形ABC中,点E是AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图①,若点D在BC上,求证:CE+CF=CD.
【类比探究】
如图②,若点D在BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图, △ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点, 且DE⊥AC,EF⊥BC, DF⊥AB,计算△DEF各个内角的度数.
解题秘方:紧扣等边三角形的三个内角都等于60°,求角的度数.
解:∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵ DE⊥AC,EF⊥BC,DF⊥AB,
∴∠AED=∠EFC=∠FDB=90°,
∴∠ADE=90°-∠A=90°-60°=30°,
∴∠EDF=180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
∴△DEF各个内角的度数都是60°.
【例2】如图,等边三角形ABC的边长为3,D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化.
解: ∵△ABC是等边三角形,D是AC的中点,
∴ ∠ABC=∠ACB=60 °, ∠DBE=∠ABC=30 °,
CD=AC=. ∵ DE=DB,∴∠E=∠DBE=30°.
∵∠ACB=∠CDE+∠E,
∴∠CDE=∠ACB-∠E=30°.∴∠CDE=∠E.
∴ CD=CE. ∴ CE=CD=.
【例3】如图,已知△ABC为等边三角形,点D,E分别在BC,AC边上,且 AE=CD,AD与BE相交于点F.
解题秘方:利用等边三角形中边相等、角相等且为60°的性质进行解答.
(1)求证:△ABE≌△CAD;
证明:∵△ABC为等边三角形,
∴∠BAE=∠ACD=60°,AB=CA.
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS).
(2)求∠BFD的度数.
解:∵△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAF,
∴∠BFD=∠CAD+∠BAF=∠BAC=60°.
【例4】如图,在等边三角形ABC中, ∠ABC和∠ACB的平分线相交于点O,OB,OC的垂直平分线分别交BC于点E,F,连接OE,OF. 求证:△OEF 是等边三角形.
解题秘方:利用等边三角形的判定定理1, 通过求∠OEF=∠OFE=∠EOF=60°,得△OEF是等边三角形.
证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.
∵ CO,BO分别平分∠ACB,∠ABC,∴∠OBE=∠OCF=30°. ∵ OB,OC的垂直平分线分别交BC于点E,F, ∴ OE=BE,OF=FC,∴∠BOE=∠OBE=30°,∠COF=∠OCF=30°. ∴∠OEF=∠BOE+∠OBE=60°,∠OFE=∠COF+∠OCF=60°. ∴∠EOF=60°. ∴∠OEF=∠OFE=∠EOF. ∴△OEF是等边三角形.
【例5】如图, 点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN,MC相交于点E,BM,CN相交于点F. 连接EF,求证:
(1)AN=BM;
解题秘方:要证AN=BM,只需证△ACN≌△MCB;
证明:∵△ACM,△CBN都是等边三角形,
∴ AC=CM,CN=BC,∠ACM=∠BCN=60°.
∴∠ACM+∠MCN=∠BCN+∠MCN,
即∠ACN=∠MCB.
在△ACN和△MCB中,
∴△ACN≌△MCB(SAS),∴ AN=BM.
(2)△CEF是等边三角形.
解题秘方:根据已知条件,易求∠ ECF=60°,故证明△ECF为等腰三角形即可.
证明:∵△ACN≌△MCB,∴∠ENC=∠FBC.
∵∠ECN=180°-∠ACM-∠NCB=60°,
∴∠ECN=∠FCB.
在△ECN和△FCB中,
∴△ECN≌△FCB(ASA). ∴ CE=CF.
又∵∠ECF=60°,∴△CEF是等边三角形.
【同步练习】
一、选择题
1.下列性质中,等边三角形具有且等腰三角形也具有的是( D )
A.三条边相等 B.三个内角相等
C.有三条对称轴 D.是轴对称图形
2.如图,一张等边三角形纸片,剪去一个角后得到一张四边形纸片,则图中∠α+∠β的度数是( C )
A. 180° B. 220° C. 240° D. 300°
第2题图 第4题图 第5题图
3.关于等边三角形的说法:①等边三角形有三条对称轴;②有一个角等于60°的等腰三角形是等边三角形;③有两个角等于60°的三角形是等边三角形;④有两个角相等的等腰三角形是等边三角形.其中正确的说法有( C )
A.1个 B.2个 C.3个 D.4个
4.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( A )
A.15° B.30° C.45° D.60°
5.【2021·益阳】如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( C )
A.40° B.30° C.20° D.15°
6.【2021·福建】如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于( C )
A.108° B.120° C.126° D.132°
第6题图 第7题图 第8题图
7.如图,等边三角形ABC的边长为2,CD平分∠ACB,交AB于点D,DE∥BC,则△ADE的周长为( C )
A.2 B.2.5 C.3 D.4
8.如图,D,E,F分别是等边三角形ABC各边上的点,且AD=BE=CF,则△DEF的形状是( A )
A.等边三角形 B.腰和底边不相等的等腰三角形
C.直角三角形 D.不等边三角形
9.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为( A )
A.1.6 B.1.8 C.2 D.2.6
第9题图 第10题图 第11题图
10.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( B )
A.9 B.8 C.6 D.7
11.如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连接BE,AD,M,N分别是线段BE,AD上的两点,且BM=BE,AN=AD,则△CMN的形状是( C )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
二、填空题
12.等边三角形的三个内角都________,并且每一个角都等于________.
【答案】相等 60°
13.三个角都________的三角形是等边三角形;有一个角是________的等腰三角形是等边三角形.
【答案】相等 60°
14.如图,在等边三角形ABC中,AD⊥BC,AB=5 cm,则DC的长为________________.
【答案】2.5 cm
第14题图 第15题图 第16题图
15.已知D,E分别是等边三角形ABC中AB,AC上的点,且AE=BD,则BE与CD的夹角是_______________.
【答案】60°或120°
16.如图,△ABC中,∠ACB=90°,AC=BC,D为AB边上一点,且∠ADC=60°,沿CD翻折△CBD,点B落在点B′的位置,连接AB′,则B′A∶AC的值为 .
【答案】1
17.如图,在△ABC中,AB=BC=4,∠ACB=60°,BD是∠ABC的平分线,若M, N分别是BD和BC上的动点,当CM+MN取最小值时,BN的值是___.
【答案】2
三、解答题
18.如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为边作等边三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
解:AE∥BC.理由如下:
∵△ABC与△CDE都为等边三角形,
∴BC=AC,CD=CE,∠B=∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE.
∴△BCD≌△ACE(SAS).∴∠B=∠EAC.
∴∠EAC=∠ACB.∴AE∥BC.
19.如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
证明:∵D为AB的中点,
∴AD=BD.
∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,
∴Rt△ADE≌Rt△BDF(HL).
∴∠A=∠B.∴AC=BC.
∵AB=AC,∴AB=BC=AC.
∴△ABC是等边三角形.
20.如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程.
解:(1)△ODE是等边三角形.
理由:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,
∠OED=∠ACB=60°.
∴△ODE是等边三角形.
(2)BD=DE=EC.
理由:∵OB平分∠ABC,∴∠ABO=∠OBD.
∵OD∥AB,∴∠BOD=∠ABO.
∴∠OBD=∠BOD.∴BD=OD.
同理可得EC=EO.
∵△ODE是等边三角形,∴DE=OD=OE.
∴BD=DE=EC.
21.(1)如图①,在等边三角形ABC中,M是BC上的任意一点(不含端点B,C),连接AM,以AM为边作等边三角形AMN,连接CN.求证:∠ABC=∠ACN;
(2)如图②,在等边三角形ABC中,M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中的结论∠ABC=∠ACN还成立吗?请说明理由.
解:(1)证明:∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°.
∴∠BAM=∠CAN.
∴△BAM≌△CAN(SAS).
∴∠ABC=∠ACN.
(2)结论∠ABC=∠ACN仍成立.理由如下:
∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN.∠BAC=∠MAN=60°.
∴∠BAM=∠CAN.∴△BAM≌△CAN(SAS).
∴∠ABC=∠ACN.
22.如图,在等边三角形ABC中,点E是AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图①,若点D在BC上,求证:CE+CF=CD.
【总结】证明一个三角形是等边三角形的思路:
1.若已知三边关系,则选用等边三角形的定义来判定.
2.若已知三角关系,则选用“三个角都相等的三角形是等边三角形”来判定.
3.若已知是等腰三角形,则选用“有一个角是60°的等腰三角形是等边三角形”来判定.
证明:在CD上截取CH=CE,连接EH,如图①所示.
∵△ABC是等边三角形,∴∠ECH=60°.
∴△CEH是等边三角形.∴EH=EC=CH,∠CEH=60°.
∵△DEF是等边三角形,∴DE=FE,∠DEF=60°.
∴∠DEH+∠HEF=∠FEC+∠HEF=60°.
∴∠DEH=∠FEC.
在△DEH和△FEC中,
∴△DEH≌△FEC(SAS).∴DH=CF.
∴CD=CH+DH=CE+CF,
即CE+CF=CD.
【类比探究】
如图②,若点D在BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
解:线段CE,CF与CD之间的数量关系是FC=CD+CE.
理由如下:
∵△ABC是等边三角形,∴∠A=∠B=60°.
过D作DG∥AB,交AC的延长线于点G,
如图②所示.
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=∠DCG=60°.
∴△GCD为等边三角形.∴DG=CD=CG.
∵△EDF为等边三角形,
∴ED=FD,∠EDF=∠GDC=60°.
∴∠EDG=∠FDC.
在△EGD和△FCD中,
∴△EGD≌△FCD(SAS).∴EG=CF.
∵EG=CG+CE=CD+CE,
∴CF=CD+CE.
第1课时 等边三角形的性质和判定
【知识重点】
知识点1 等边三角形的定义及性质
1. 定义 三边都相等的三角形叫做等边三角形,也叫正三角形.
2. 性质
(1)等边三角形的三条边都相等.
(2)等边三角形的三个内角都相等,并且每一个角都等于60°.
(3)等边三角形是轴对称图形,它有3 条对称轴,分别为三边的垂直平分线.
(4)各边上的高、中线、对角的角平分线重合,且长度相等.
特别解读
等边三角形是特殊的等腰三角形,具备等腰三角形的所有性质:
(1)任意两边都可以作为腰.
(2)任意一个角都可以作为顶角.
(3)任意一边上的“三线合一”.
知识点2 等边三角形的判定
1. 判定定理1 三个角都相等的三角形是等边三角形.
几何语言:如图,在△ABC中,
∵∠A=∠B=∠C,
∴△ABC是等边三角形.
2. 判定定理2 有一个角是60°的等腰三角形是等边三角形.
几何语言:如图,在△ ABC 中,
∵ AB=AC,∠A=60°或∠B=60°
或∠C=60°,
∴△ABC是等边三角形.
证明等边三角形的思维导图:
特别解读
1. 在等腰三角形中,只要有一个角是60°,无论这个角是顶角还是底角,判定定理2都成立.
2. 等边三角形的判定方法:
(1) 若已知三边关系,一般选用定义判定;
(2) 若已知三角关系,一般选用判定定理1判定;
(3) 若已知该三角形是等腰三角形,一般选用判定定理2判定.
【经典例题】
【例1】如图, △ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点, 且DE⊥AC,EF⊥BC, DF⊥AB,计算△DEF各个内角的度数.
解题秘方:紧扣等边三角形的三个内角都等于60°,求角的度数.
【例2】如图,等边三角形ABC的边长为3,D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化.
【例3】如图,已知△ABC为等边三角形,点D,E分别在BC,AC边上,且 AE=CD,AD与BE相交于点F.
解题秘方:利用等边三角形中边相等、角相等且为60°的性质进行解答.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
【例4】如图,在等边三角形ABC中, ∠ABC和∠ACB的平分线相交于点O,OB,OC的垂直平分线分别交BC于点E,F,连接OE,OF. 求证:△OEF 是等边三角形.
解题秘方:利用等边三角形的判定定理1, 通过求∠OEF=∠OFE=∠EOF=60°,得△OEF是等边三角形.
【例5】如图, 点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN,MC相交于点E,BM,CN相交于点F. 连接EF,求证:
(1)AN=BM;
解题秘方:要证AN=BM,只需证△ACN≌△MCB;
(2)△CEF是等边三角形.
解题秘方:根据已知条件,易求∠ ECF=60°,故证明△ECF为等腰三角形即可.
【同步练习】
一、选择题
1.下列性质中,等边三角形具有且等腰三角形也具有的是( )
A.三条边相等 B.三个内角相等
C.有三条对称轴 D.是轴对称图形
2.如图,一张等边三角形纸片,剪去一个角后得到一张四边形纸片,则图中∠α+∠β的度数是( )
A. 180° B. 220° C. 240° D. 300°
第2题图 第4题图 第5题图
3.关于等边三角形的说法:①等边三角形有三条对称轴;②有一个角等于60°的等腰三角形是等边三角形;③有两个角等于60°的三角形是等边三角形;④有两个角相等的等腰三角形是等边三角形.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
5.【2021·益阳】如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
6.【2021·福建】如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于( )
A.108° B.120° C.126° D.132°
第6题图 第7题图 第8题图
7.如图,等边三角形ABC的边长为2,CD平分∠ACB,交AB于点D,DE∥BC,则△ADE的周长为( )
A.2 B.2.5 C.3 D.4
8.如图,D,E,F分别是等边三角形ABC各边上的点,且AD=BE=CF,则△DEF的形状是( )
A.等边三角形 B.腰和底边不相等的等腰三角形
C.直角三角形 D.不等边三角形
9.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为( )
A.1.6 B.1.8 C.2 D.2.6
第9题图 第10题图 第11题图
10.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( )
A.9 B.8 C.6 D.7
11.如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连接BE,AD,M,N分别是线段BE,AD上的两点,且BM=BE,AN=AD,则△CMN的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
二、填空题
12.等边三角形的三个内角都________,并且每一个角都等于________.
13.三个角都________的三角形是等边三角形;有一个角是________的等腰三角形是等边三角形.
14.如图,在等边三角形ABC中,AD⊥BC,AB=5 cm,则DC的长为________________.
第14题图 第15题图 第16题图
15.已知D,E分别是等边三角形ABC中AB,AC上的点,且AE=BD,则BE与CD的夹角是_______________.
16.如图,△ABC中,∠ACB=90°,AC=BC,D为AB边上一点,且∠ADC=60°,沿CD翻折△CBD,点B落在点B′的位置,连接AB′,则B′A∶AC的值为 .
17.如图,在△ABC中,AB=BC=4,∠ACB=60°,BD是∠ABC的平分线,若M, N分别是BD和BC上的动点,当CM+MN取最小值时,BN的值是___.
三、解答题
18.如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为边作等边三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
19.如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
20.如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程.
21.(1)如图①,在等边三角形ABC中,M是BC上的任意一点(不含端点B,C),连接AM,以AM为边作等边三角形AMN,连接CN.求证:∠ABC=∠ACN;
(2)如图②,在等边三角形ABC中,M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中的结论∠ABC=∠ACN还成立吗?请说明理由.
22.如图,在等边三角形ABC中,点E是AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图①,若点D在BC上,求证:CE+CF=CD.
【类比探究】
如图②,若点D在BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图, △ABC是等边三角形,D,E,F分别是三边AB,AC,BC上的点, 且DE⊥AC,EF⊥BC, DF⊥AB,计算△DEF各个内角的度数.
解题秘方:紧扣等边三角形的三个内角都等于60°,求角的度数.
解:∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.
∵ DE⊥AC,EF⊥BC,DF⊥AB,
∴∠AED=∠EFC=∠FDB=90°,
∴∠ADE=90°-∠A=90°-60°=30°,
∴∠EDF=180°-30°-90°=60°.
同理可得∠DEF=∠EFD=60°.
∴△DEF各个内角的度数都是60°.
【例2】如图,等边三角形ABC的边长为3,D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化.
解: ∵△ABC是等边三角形,D是AC的中点,
∴ ∠ABC=∠ACB=60 °, ∠DBE=∠ABC=30 °,
CD=AC=. ∵ DE=DB,∴∠E=∠DBE=30°.
∵∠ACB=∠CDE+∠E,
∴∠CDE=∠ACB-∠E=30°.∴∠CDE=∠E.
∴ CD=CE. ∴ CE=CD=.
【例3】如图,已知△ABC为等边三角形,点D,E分别在BC,AC边上,且 AE=CD,AD与BE相交于点F.
解题秘方:利用等边三角形中边相等、角相等且为60°的性质进行解答.
(1)求证:△ABE≌△CAD;
证明:∵△ABC为等边三角形,
∴∠BAE=∠ACD=60°,AB=CA.
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS).
(2)求∠BFD的度数.
解:∵△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAF,
∴∠BFD=∠CAD+∠BAF=∠BAC=60°.
【例4】如图,在等边三角形ABC中, ∠ABC和∠ACB的平分线相交于点O,OB,OC的垂直平分线分别交BC于点E,F,连接OE,OF. 求证:△OEF 是等边三角形.
解题秘方:利用等边三角形的判定定理1, 通过求∠OEF=∠OFE=∠EOF=60°,得△OEF是等边三角形.
证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.
∵ CO,BO分别平分∠ACB,∠ABC,∴∠OBE=∠OCF=30°. ∵ OB,OC的垂直平分线分别交BC于点E,F, ∴ OE=BE,OF=FC,∴∠BOE=∠OBE=30°,∠COF=∠OCF=30°. ∴∠OEF=∠BOE+∠OBE=60°,∠OFE=∠COF+∠OCF=60°. ∴∠EOF=60°. ∴∠OEF=∠OFE=∠EOF. ∴△OEF是等边三角形.
【例5】如图, 点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN,MC相交于点E,BM,CN相交于点F. 连接EF,求证:
(1)AN=BM;
解题秘方:要证AN=BM,只需证△ACN≌△MCB;
证明:∵△ACM,△CBN都是等边三角形,
∴ AC=CM,CN=BC,∠ACM=∠BCN=60°.
∴∠ACM+∠MCN=∠BCN+∠MCN,
即∠ACN=∠MCB.
在△ACN和△MCB中,
∴△ACN≌△MCB(SAS),∴ AN=BM.
(2)△CEF是等边三角形.
解题秘方:根据已知条件,易求∠ ECF=60°,故证明△ECF为等腰三角形即可.
证明:∵△ACN≌△MCB,∴∠ENC=∠FBC.
∵∠ECN=180°-∠ACM-∠NCB=60°,
∴∠ECN=∠FCB.
在△ECN和△FCB中,
∴△ECN≌△FCB(ASA). ∴ CE=CF.
又∵∠ECF=60°,∴△CEF是等边三角形.
【同步练习】
一、选择题
1.下列性质中,等边三角形具有且等腰三角形也具有的是( D )
A.三条边相等 B.三个内角相等
C.有三条对称轴 D.是轴对称图形
2.如图,一张等边三角形纸片,剪去一个角后得到一张四边形纸片,则图中∠α+∠β的度数是( C )
A. 180° B. 220° C. 240° D. 300°
第2题图 第4题图 第5题图
3.关于等边三角形的说法:①等边三角形有三条对称轴;②有一个角等于60°的等腰三角形是等边三角形;③有两个角等于60°的三角形是等边三角形;④有两个角相等的等腰三角形是等边三角形.其中正确的说法有( C )
A.1个 B.2个 C.3个 D.4个
4.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( A )
A.15° B.30° C.45° D.60°
5.【2021·益阳】如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( C )
A.40° B.30° C.20° D.15°
6.【2021·福建】如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,则∠AFC等于( C )
A.108° B.120° C.126° D.132°
第6题图 第7题图 第8题图
7.如图,等边三角形ABC的边长为2,CD平分∠ACB,交AB于点D,DE∥BC,则△ADE的周长为( C )
A.2 B.2.5 C.3 D.4
8.如图,D,E,F分别是等边三角形ABC各边上的点,且AD=BE=CF,则△DEF的形状是( A )
A.等边三角形 B.腰和底边不相等的等腰三角形
C.直角三角形 D.不等边三角形
9.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为( A )
A.1.6 B.1.8 C.2 D.2.6
第9题图 第10题图 第11题图
10.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( B )
A.9 B.8 C.6 D.7
11.如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连接BE,AD,M,N分别是线段BE,AD上的两点,且BM=BE,AN=AD,则△CMN的形状是( C )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
二、填空题
12.等边三角形的三个内角都________,并且每一个角都等于________.
【答案】相等 60°
13.三个角都________的三角形是等边三角形;有一个角是________的等腰三角形是等边三角形.
【答案】相等 60°
14.如图,在等边三角形ABC中,AD⊥BC,AB=5 cm,则DC的长为________________.
【答案】2.5 cm
第14题图 第15题图 第16题图
15.已知D,E分别是等边三角形ABC中AB,AC上的点,且AE=BD,则BE与CD的夹角是_______________.
【答案】60°或120°
16.如图,△ABC中,∠ACB=90°,AC=BC,D为AB边上一点,且∠ADC=60°,沿CD翻折△CBD,点B落在点B′的位置,连接AB′,则B′A∶AC的值为 .
【答案】1
17.如图,在△ABC中,AB=BC=4,∠ACB=60°,BD是∠ABC的平分线,若M, N分别是BD和BC上的动点,当CM+MN取最小值时,BN的值是___.
【答案】2
三、解答题
18.如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为边作等边三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
解:AE∥BC.理由如下:
∵△ABC与△CDE都为等边三角形,
∴BC=AC,CD=CE,∠B=∠ACB=∠DCE=60°.
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE.
∴△BCD≌△ACE(SAS).∴∠B=∠EAC.
∴∠EAC=∠ACB.∴AE∥BC.
19.如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
证明:∵D为AB的中点,
∴AD=BD.
∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,
∴Rt△ADE≌Rt△BDF(HL).
∴∠A=∠B.∴AC=BC.
∵AB=AC,∴AB=BC=AC.
∴△ABC是等边三角形.
20.如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程.
解:(1)△ODE是等边三角形.
理由:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,
∠OED=∠ACB=60°.
∴△ODE是等边三角形.
(2)BD=DE=EC.
理由:∵OB平分∠ABC,∴∠ABO=∠OBD.
∵OD∥AB,∴∠BOD=∠ABO.
∴∠OBD=∠BOD.∴BD=OD.
同理可得EC=EO.
∵△ODE是等边三角形,∴DE=OD=OE.
∴BD=DE=EC.
21.(1)如图①,在等边三角形ABC中,M是BC上的任意一点(不含端点B,C),连接AM,以AM为边作等边三角形AMN,连接CN.求证:∠ABC=∠ACN;
(2)如图②,在等边三角形ABC中,M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中的结论∠ABC=∠ACN还成立吗?请说明理由.
解:(1)证明:∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°.
∴∠BAM=∠CAN.
∴△BAM≌△CAN(SAS).
∴∠ABC=∠ACN.
(2)结论∠ABC=∠ACN仍成立.理由如下:
∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN.∠BAC=∠MAN=60°.
∴∠BAM=∠CAN.∴△BAM≌△CAN(SAS).
∴∠ABC=∠ACN.
22.如图,在等边三角形ABC中,点E是AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图①,若点D在BC上,求证:CE+CF=CD.
【总结】证明一个三角形是等边三角形的思路:
1.若已知三边关系,则选用等边三角形的定义来判定.
2.若已知三角关系,则选用“三个角都相等的三角形是等边三角形”来判定.
3.若已知是等腰三角形,则选用“有一个角是60°的等腰三角形是等边三角形”来判定.
证明:在CD上截取CH=CE,连接EH,如图①所示.
∵△ABC是等边三角形,∴∠ECH=60°.
∴△CEH是等边三角形.∴EH=EC=CH,∠CEH=60°.
∵△DEF是等边三角形,∴DE=FE,∠DEF=60°.
∴∠DEH+∠HEF=∠FEC+∠HEF=60°.
∴∠DEH=∠FEC.
在△DEH和△FEC中,
∴△DEH≌△FEC(SAS).∴DH=CF.
∴CD=CH+DH=CE+CF,
即CE+CF=CD.
【类比探究】
如图②,若点D在BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
解:线段CE,CF与CD之间的数量关系是FC=CD+CE.
理由如下:
∵△ABC是等边三角形,∴∠A=∠B=60°.
过D作DG∥AB,交AC的延长线于点G,
如图②所示.
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=∠DCG=60°.
∴△GCD为等边三角形.∴DG=CD=CG.
∵△EDF为等边三角形,
∴ED=FD,∠EDF=∠GDC=60°.
∴∠EDG=∠FDC.
在△EGD和△FCD中,
∴△EGD≌△FCD(SAS).∴EG=CF.
∵EG=CG+CE=CD+CE,
∴CF=CD+CE.
