13.3.2.2 含30°角的直角三角形的性质同步练习 (含答案)
文档属性
| 名称 | 13.3.2.2 含30°角的直角三角形的性质同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 19:51:36 | ||
图片预览


文档简介
13.3.2等边三角形
第2课时 含30°角的直角三角形的性质
【知识重点】
知识点1 含30°角的直角三角形的性质
1. 性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半 .
几何语言:如图,在Rt△ABC中,
∵∠C=90°,∠A=30°,∴ BC=AB.
2. 作用:应用于证线段的倍分关系和计算角度.
特别解读
应用此性质,必须满足两个条件:
①在直角三角形中;
②有一个锐角为30 ° .二者缺一不可.
【经典例题】
【例1】如图,在Rt△ABC中 ,∠C=90°,AB边的垂直平分线MN交AB于点M,交BC于点N,且∠B=15°,AC=4 cm,求BN的长.
解题秘方:先构造含30°角的直角三角形,再利用含30°角的直角三角形的性质求线段长.
【总结】(1) 求某直角三角形的边长时,考虑构造含30°角的直角三角形.
(2) 若给出的是15°角,则构造以15°角为底角的等腰三角形,其顶角处的外角为30°的角.
【例2】如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q. 求证:BP=2PQ.
方法点拨:在同一个三角形中证明一条线段等于另一条线段的2倍,一是证明是直角三角形;二是证明较短的直角边所对的锐角等于30°
【同步练习】
一、选择题
1.在Rt△ABC中,∠C=90°,∠B=30°,则( )
A.AB=2AC B.AC=2AB C.AB=AC D.AB=3AC
2.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12cm,则AB等于( )
A.6cm B.7cm C.8cm D.9cm
3.如图,在△ABC中,∠B=∠C=60°,点D为AB边的中点,DE⊥BC,若BE=1,则AC的长为( )
A.2 B.3 C.4 D.6
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=6,∠ABC=60°,点D在边BC上,且AD=AC,若CD=2,则BD的长为( )
A.1.5 B.2 C.2.5 D.3
5.如图,在△ABC中, ∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( )
A.BD=BC B.BD=BC C.BD=BC D.BD=BC
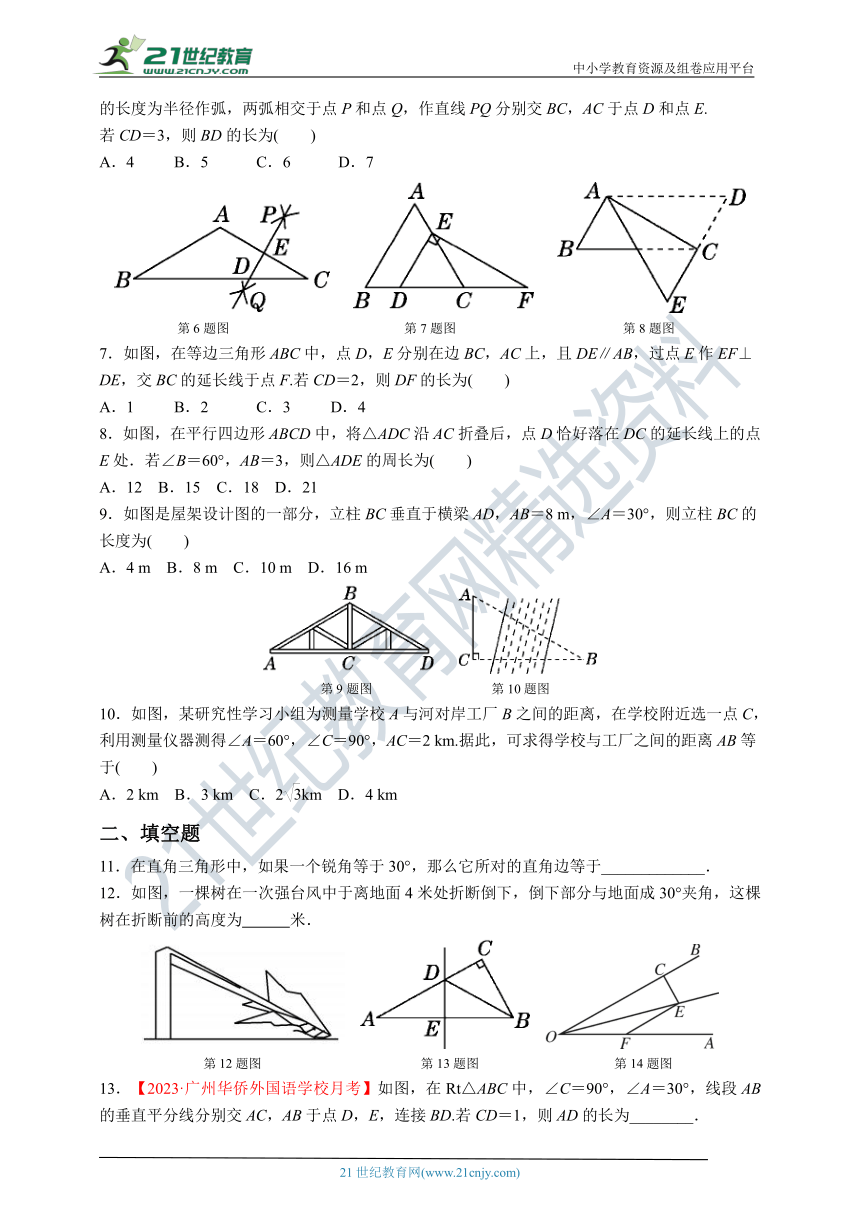
6.【2022·淄博】如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.
若CD=3,则BD的长为( )
A.4 B.5 C.6 D.7
第6题图 第7题图 第8题图
7.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.若CD=2,则DF的长为( )
A.1 B.2 C.3 D.4
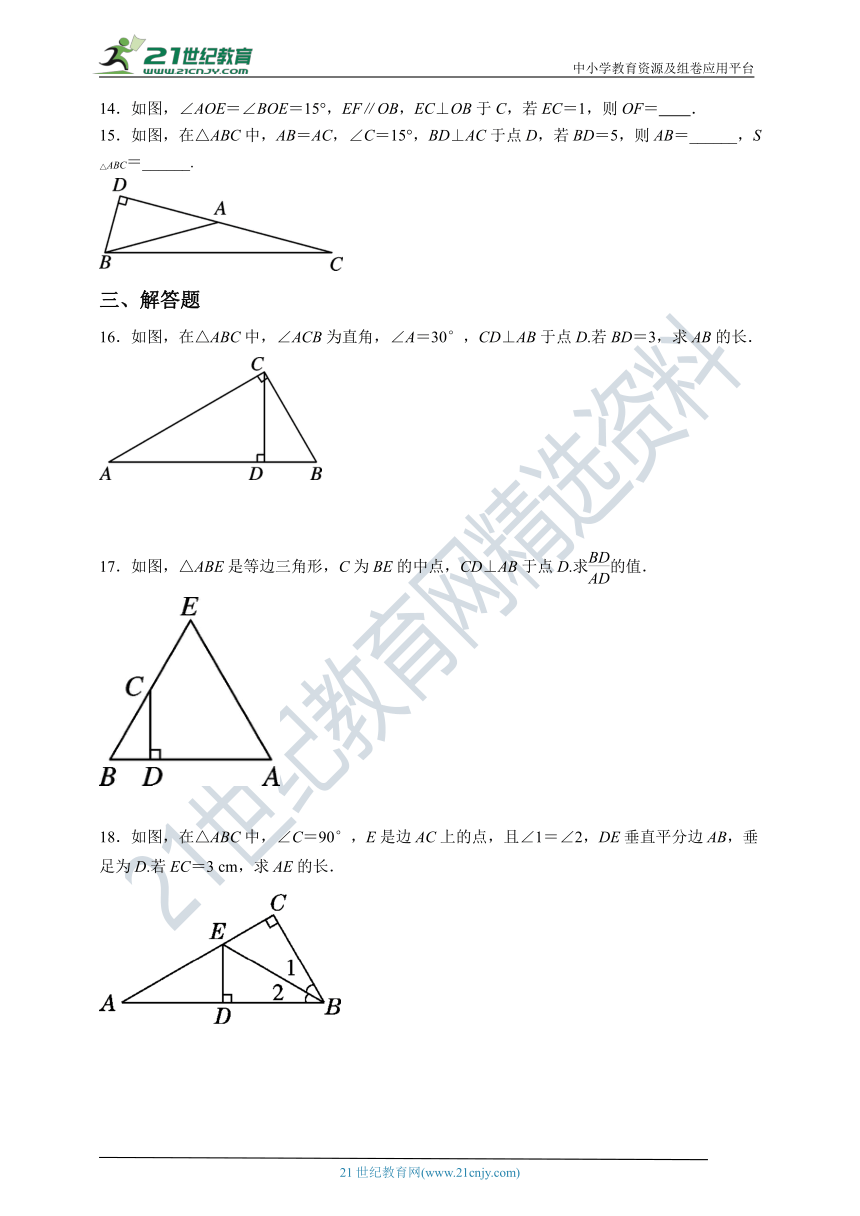
8.如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( )
A.12 B.15 C.18 D.21
9.如图是屋架设计图的一部分,立柱BC垂直于横梁AD,AB=8 m,∠A=30°,则立柱BC的长度为( )
A.4 m B.8 m C.10 m D.16 m
第9题图 第10题图
10.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可求得学校与工厂之间的距离AB等于( )
A.2 km B.3 km C.2km D.4 km
二、填空题
11.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于_____________.
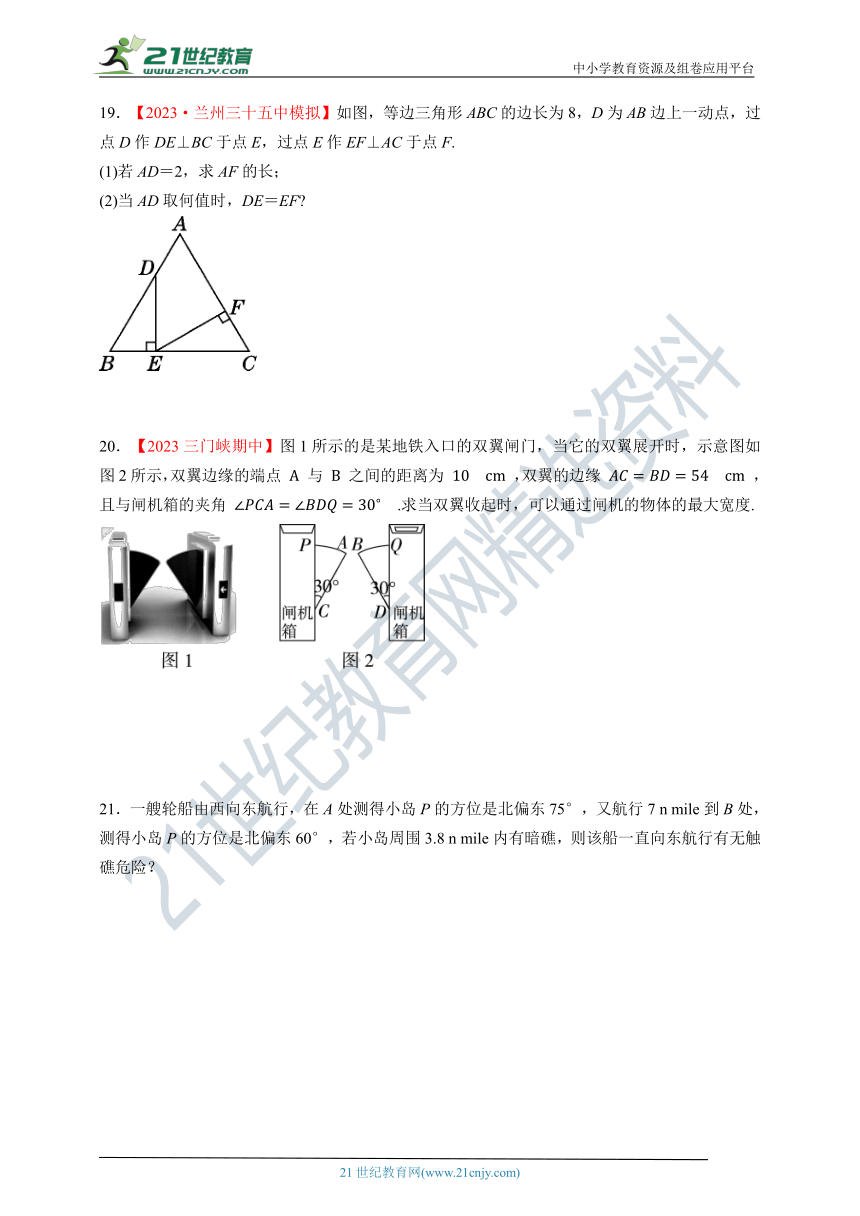
12.如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为 米.
第12题图 第13题图 第14题图
13.【2023·广州华侨外国语学校月考】如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为________.
14.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= .
15.如图,在△ABC中,AB=AC,∠C=15°,BD⊥AC于点D,若BD=5,则AB=______,S△ABC=______.
三、解答题
16.如图,在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于点D.若BD=3,求AB的长.
17.如图,△ABE是等边三角形,C为BE的中点,CD⊥AB于点D.求的值.
18.如图,在△ABC中,∠C=90°,E是边AC上的点,且∠1=∠2,DE垂直平分边AB,垂足为D.若EC=3 cm,求AE的长.
19.【2023·兰州三十五中模拟】如图,等边三角形ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
(2)当AD取何值时,DE=EF
20.【2023三门峡期中】图1所示的是某地铁入口的双翼闸门,当它的双翼展开时,示意图如图2所示,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机箱的夹角 .求当双翼收起时,可以通过闸机的物体的最大宽度.
21.一艘轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又航行7 n mile到B处,测得小岛P的方位是北偏东60°,若小岛周围3.8 n mile内有暗礁,则该船一直向东航行有无触礁危险?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,在Rt△ABC中 ,∠C=90°,AB边的垂直平分线MN交AB于点M,交BC于点N,且∠B=15°,AC=4 cm,求BN的长.
解题秘方:先构造含30°角的直角三角形,再利用含30°角的直角三角形的性质求线段长.
解:如图,连接AN.
∵ MN为AB边的垂直平分线,
∴ AN=BN,
∴∠NAB=∠B=15°,
∴∠ANC=∠B+∠NAB=30°.
在Rt△ACN中,∠ANC=30°,
∴ AN=2AC=2×4=8(cm). ∴ BN=8 cm.
【总结】(1) 求某直角三角形的边长时,考虑构造含30°角的直角三角形.
(2) 若给出的是15°角,则构造以15°角为底角的等腰三角形,其顶角处的外角为30°的角.
【例2】如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q. 求证:BP=2PQ.
解题秘方:利用含30°角的直角三角形的性质证明线段的倍分关系.
证明:∵△ABC是等边三角形,
∴ AB=AC,∠BAE=∠C=60°.
∵ AE=CD,∴△ABE≌△CAD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAE=60°.
∵ BQ⊥AD,∴∠PBQ=30°,∴ BP=2PQ.
方法点拨:在同一个三角形中证明一条线段等于另一条线段的2倍,一是证明是直角三角形;二是证明较短的直角边所对的锐角等于30°
【同步练习】
一、选择题
1.在Rt△ABC中,∠C=90°,∠B=30°,则( A )
A.AB=2AC B.AC=2AB C.AB=AC D.AB=3AC
2.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12cm,则AB等于( C )
A.6cm B.7cm C.8cm D.9cm
3.如图,在△ABC中,∠B=∠C=60°,点D为AB边的中点,DE⊥BC,若BE=1,则AC的长为( C )
A.2 B.3 C.4 D.6
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=6,∠ABC=60°,点D在边BC上,且AD=AC,若CD=2,则BD的长为( B )
A.1.5 B.2 C.2.5 D.3
5.如图,在△ABC中, ∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( C )
A.BD=BC B.BD=BC C.BD=BC D.BD=BC
6.【2022·淄博】如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.
若CD=3,则BD的长为( C )
A.4 B.5 C.6 D.7
【解析】如图,连接AD.∵AB=AC,∠A=120°,
∴∠B=∠C=30°.由作法得DE垂直平分AC,
∴DA=DC=3.∴∠DAC=∠C=30°.∴∠BAD=120°-30°=90°.
在Rt△ABD中,∵∠B=30°,∴BD=2AD=6.
第6题图 第7题图 第8题图
7.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.若CD=2,则DF的长为( D )
A.1 B.2 C.3 D.4
8.如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( C )
A.12 B.15 C.18 D.21
9.如图是屋架设计图的一部分,立柱BC垂直于横梁AD,AB=8 m,∠A=30°,则立柱BC的长度为( A )
A.4 m B.8 m C.10 m D.16 m
第9题图 第10题图
10.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可求得学校与工厂之间的距离AB等于( D )
A.2 km B.3 km C.2km D.4 km
二、填空题
11.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于_____________.
【答案】斜边的一半
12.如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为 米.
【答案】12
第12题图 第13题图 第14题图
13.【2023·广州华侨外国语学校月考】如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为________.
【提示】已知∠A=30°,∠DEA=90°,欲求AD的长,只需求出DE的长,容易证得DE=CD.
【答案】2
14.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= .
【答案】2
15.如图,在△ABC中,AB=AC,∠C=15°,BD⊥AC于点D,若BD=5,则AB=______,S△ABC=______.
【答案】10 25
三、解答题
16.如图,在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于点D.若BD=3,求AB的长.
解:∵∠ACB=90°,
CD⊥AB,
∴∠BCD=∠A=30°,
∴BC=2BD=6.
在Rt△ABC中,∠A=30°,BC=6,
∴AB=2BC=12.
17.如图,△ABE是等边三角形,C为BE的中点,CD⊥AB于点D.求的值.
解:连接AC.∵C为BE的中点,△ABE为等边三角形,
∴AC⊥BE,∠BCD=∠BAC=30°,
设BD=x,则BC=2x,AB=4x,
∴AD=3x,∴=.
18.如图,在△ABC中,∠C=90°,E是边AC上的点,且∠1=∠2,DE垂直平分边AB,垂足为D.若EC=3 cm,求AE的长.
解:∵DE垂直平分边AB,∴AE=BE.∴∠2=∠A.
∵∠1=∠2,∴∠A=∠1=∠2.∵∠C=90°,
∴∠A=∠1=∠2=30°.∵∠1=∠2,ED⊥AB,∠C=90°,
∴CE=DE=3 cm.
在Rt△ADE中,∵∠ADE=90°,∠A=30°,
∴AE=2DE=2×3=6(cm).
19.【2023·兰州三十五中模拟】如图,等边三角形ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
解:(1)由题意知AB=BC=AC=8,∠B=∠A=∠C=60°,
∴BD=AB-AD=8-2=6.∵DE⊥BC,
∴∠BDE=90°-60°=30°.∴BE=BD=3.
∴EC=8-3=5.∵EF⊥AC,∴∠FEC=90°-60°=30°.
∴FC=5×=.∴AF=8-=.
(2)当AD取何值时,DE=EF
当DE=EF时,易证△BDE≌△CEF,
∴BE=CF,BD=CE.
∵CF=CE,∴BE=CE.
又∵BE+CE=8,∴CE=∴BD=
∴AD=8-=.即当AD=时,DE=EF.
20.【2023三门峡期中】图1所示的是某地铁入口的双翼闸门,当它的双翼展开时,示意图如图2所示,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机箱的夹角 .求当双翼收起时,可以通过闸机的物体的最大宽度.
解:如图,分别过点 , 作 于点 , 于点 ,
在 中, , ,
,
同理可得, .
点 与点 之间的距离为 ,
当双翼收起时,可以通过闸机的物体的最大宽度为
.
21.一艘轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又航行7 n mile到B处,测得小岛P的方位是北偏东60°,若小岛周围3.8 n mile内有暗礁,则该船一直向东航行有无触礁危险?
解:依题意画示意图,则AB=7 n mile,过点P作PC⊥AB,垂足为C,则∠PBC=30°,
∴∠APB=∠PBC-∠PAB=30°-15°=15°.
∴∠PAB=∠APB.
∴PB=AB=7 n mile.
∴PC=PB=×7=3.5 n mile.
∵PC<3.8 n mile,
∴该船一直向东航行有触礁的危险.
第2课时 含30°角的直角三角形的性质
【知识重点】
知识点1 含30°角的直角三角形的性质
1. 性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半 .
几何语言:如图,在Rt△ABC中,
∵∠C=90°,∠A=30°,∴ BC=AB.
2. 作用:应用于证线段的倍分关系和计算角度.
特别解读
应用此性质,必须满足两个条件:
①在直角三角形中;
②有一个锐角为30 ° .二者缺一不可.
【经典例题】
【例1】如图,在Rt△ABC中 ,∠C=90°,AB边的垂直平分线MN交AB于点M,交BC于点N,且∠B=15°,AC=4 cm,求BN的长.
解题秘方:先构造含30°角的直角三角形,再利用含30°角的直角三角形的性质求线段长.
【总结】(1) 求某直角三角形的边长时,考虑构造含30°角的直角三角形.
(2) 若给出的是15°角,则构造以15°角为底角的等腰三角形,其顶角处的外角为30°的角.
【例2】如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q. 求证:BP=2PQ.
方法点拨:在同一个三角形中证明一条线段等于另一条线段的2倍,一是证明是直角三角形;二是证明较短的直角边所对的锐角等于30°
【同步练习】
一、选择题
1.在Rt△ABC中,∠C=90°,∠B=30°,则( )
A.AB=2AC B.AC=2AB C.AB=AC D.AB=3AC
2.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12cm,则AB等于( )
A.6cm B.7cm C.8cm D.9cm
3.如图,在△ABC中,∠B=∠C=60°,点D为AB边的中点,DE⊥BC,若BE=1,则AC的长为( )
A.2 B.3 C.4 D.6
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=6,∠ABC=60°,点D在边BC上,且AD=AC,若CD=2,则BD的长为( )
A.1.5 B.2 C.2.5 D.3
5.如图,在△ABC中, ∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( )
A.BD=BC B.BD=BC C.BD=BC D.BD=BC
6.【2022·淄博】如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.
若CD=3,则BD的长为( )
A.4 B.5 C.6 D.7
第6题图 第7题图 第8题图
7.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.若CD=2,则DF的长为( )
A.1 B.2 C.3 D.4
8.如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( )
A.12 B.15 C.18 D.21
9.如图是屋架设计图的一部分,立柱BC垂直于横梁AD,AB=8 m,∠A=30°,则立柱BC的长度为( )
A.4 m B.8 m C.10 m D.16 m
第9题图 第10题图
10.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可求得学校与工厂之间的距离AB等于( )
A.2 km B.3 km C.2km D.4 km
二、填空题
11.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于_____________.
12.如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为 米.
第12题图 第13题图 第14题图
13.【2023·广州华侨外国语学校月考】如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为________.
14.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= .
15.如图,在△ABC中,AB=AC,∠C=15°,BD⊥AC于点D,若BD=5,则AB=______,S△ABC=______.
三、解答题
16.如图,在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于点D.若BD=3,求AB的长.
17.如图,△ABE是等边三角形,C为BE的中点,CD⊥AB于点D.求的值.
18.如图,在△ABC中,∠C=90°,E是边AC上的点,且∠1=∠2,DE垂直平分边AB,垂足为D.若EC=3 cm,求AE的长.
19.【2023·兰州三十五中模拟】如图,等边三角形ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
(2)当AD取何值时,DE=EF
20.【2023三门峡期中】图1所示的是某地铁入口的双翼闸门,当它的双翼展开时,示意图如图2所示,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机箱的夹角 .求当双翼收起时,可以通过闸机的物体的最大宽度.
21.一艘轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又航行7 n mile到B处,测得小岛P的方位是北偏东60°,若小岛周围3.8 n mile内有暗礁,则该船一直向东航行有无触礁危险?
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,在Rt△ABC中 ,∠C=90°,AB边的垂直平分线MN交AB于点M,交BC于点N,且∠B=15°,AC=4 cm,求BN的长.
解题秘方:先构造含30°角的直角三角形,再利用含30°角的直角三角形的性质求线段长.
解:如图,连接AN.
∵ MN为AB边的垂直平分线,
∴ AN=BN,
∴∠NAB=∠B=15°,
∴∠ANC=∠B+∠NAB=30°.
在Rt△ACN中,∠ANC=30°,
∴ AN=2AC=2×4=8(cm). ∴ BN=8 cm.
【总结】(1) 求某直角三角形的边长时,考虑构造含30°角的直角三角形.
(2) 若给出的是15°角,则构造以15°角为底角的等腰三角形,其顶角处的外角为30°的角.
【例2】如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q. 求证:BP=2PQ.
解题秘方:利用含30°角的直角三角形的性质证明线段的倍分关系.
证明:∵△ABC是等边三角形,
∴ AB=AC,∠BAE=∠C=60°.
∵ AE=CD,∴△ABE≌△CAD(SAS),
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAE=60°.
∵ BQ⊥AD,∴∠PBQ=30°,∴ BP=2PQ.
方法点拨:在同一个三角形中证明一条线段等于另一条线段的2倍,一是证明是直角三角形;二是证明较短的直角边所对的锐角等于30°
【同步练习】
一、选择题
1.在Rt△ABC中,∠C=90°,∠B=30°,则( A )
A.AB=2AC B.AC=2AB C.AB=AC D.AB=3AC
2.在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12cm,则AB等于( C )
A.6cm B.7cm C.8cm D.9cm
3.如图,在△ABC中,∠B=∠C=60°,点D为AB边的中点,DE⊥BC,若BE=1,则AC的长为( C )
A.2 B.3 C.4 D.6
第3题图 第4题图 第5题图
4.如图,在△ABC中,AB=6,∠ABC=60°,点D在边BC上,且AD=AC,若CD=2,则BD的长为( B )
A.1.5 B.2 C.2.5 D.3
5.如图,在△ABC中, ∠BAC=90°,∠C=30°,AD⊥BC,垂足为D,则BD与BC的数量关系是( C )
A.BD=BC B.BD=BC C.BD=BC D.BD=BC
6.【2022·淄博】如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.
若CD=3,则BD的长为( C )
A.4 B.5 C.6 D.7
【解析】如图,连接AD.∵AB=AC,∠A=120°,
∴∠B=∠C=30°.由作法得DE垂直平分AC,
∴DA=DC=3.∴∠DAC=∠C=30°.∴∠BAD=120°-30°=90°.
在Rt△ABD中,∵∠B=30°,∴BD=2AD=6.
第6题图 第7题图 第8题图
7.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.若CD=2,则DF的长为( D )
A.1 B.2 C.3 D.4
8.如图,在平行四边形ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为( C )
A.12 B.15 C.18 D.21
9.如图是屋架设计图的一部分,立柱BC垂直于横梁AD,AB=8 m,∠A=30°,则立柱BC的长度为( A )
A.4 m B.8 m C.10 m D.16 m
第9题图 第10题图
10.如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可求得学校与工厂之间的距离AB等于( D )
A.2 km B.3 km C.2km D.4 km
二、填空题
11.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于_____________.
【答案】斜边的一半
12.如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为 米.
【答案】12
第12题图 第13题图 第14题图
13.【2023·广州华侨外国语学校月考】如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC,AB于点D,E,连接BD.若CD=1,则AD的长为________.
【提示】已知∠A=30°,∠DEA=90°,欲求AD的长,只需求出DE的长,容易证得DE=CD.
【答案】2
14.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= .
【答案】2
15.如图,在△ABC中,AB=AC,∠C=15°,BD⊥AC于点D,若BD=5,则AB=______,S△ABC=______.
【答案】10 25
三、解答题
16.如图,在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于点D.若BD=3,求AB的长.
解:∵∠ACB=90°,
CD⊥AB,
∴∠BCD=∠A=30°,
∴BC=2BD=6.
在Rt△ABC中,∠A=30°,BC=6,
∴AB=2BC=12.
17.如图,△ABE是等边三角形,C为BE的中点,CD⊥AB于点D.求的值.
解:连接AC.∵C为BE的中点,△ABE为等边三角形,
∴AC⊥BE,∠BCD=∠BAC=30°,
设BD=x,则BC=2x,AB=4x,
∴AD=3x,∴=.
18.如图,在△ABC中,∠C=90°,E是边AC上的点,且∠1=∠2,DE垂直平分边AB,垂足为D.若EC=3 cm,求AE的长.
解:∵DE垂直平分边AB,∴AE=BE.∴∠2=∠A.
∵∠1=∠2,∴∠A=∠1=∠2.∵∠C=90°,
∴∠A=∠1=∠2=30°.∵∠1=∠2,ED⊥AB,∠C=90°,
∴CE=DE=3 cm.
在Rt△ADE中,∵∠ADE=90°,∠A=30°,
∴AE=2DE=2×3=6(cm).
19.【2023·兰州三十五中模拟】如图,等边三角形ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
解:(1)由题意知AB=BC=AC=8,∠B=∠A=∠C=60°,
∴BD=AB-AD=8-2=6.∵DE⊥BC,
∴∠BDE=90°-60°=30°.∴BE=BD=3.
∴EC=8-3=5.∵EF⊥AC,∴∠FEC=90°-60°=30°.
∴FC=5×=.∴AF=8-=.
(2)当AD取何值时,DE=EF
当DE=EF时,易证△BDE≌△CEF,
∴BE=CF,BD=CE.
∵CF=CE,∴BE=CE.
又∵BE+CE=8,∴CE=∴BD=
∴AD=8-=.即当AD=时,DE=EF.
20.【2023三门峡期中】图1所示的是某地铁入口的双翼闸门,当它的双翼展开时,示意图如图2所示,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机箱的夹角 .求当双翼收起时,可以通过闸机的物体的最大宽度.
解:如图,分别过点 , 作 于点 , 于点 ,
在 中, , ,
,
同理可得, .
点 与点 之间的距离为 ,
当双翼收起时,可以通过闸机的物体的最大宽度为
.
21.一艘轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又航行7 n mile到B处,测得小岛P的方位是北偏东60°,若小岛周围3.8 n mile内有暗礁,则该船一直向东航行有无触礁危险?
解:依题意画示意图,则AB=7 n mile,过点P作PC⊥AB,垂足为C,则∠PBC=30°,
∴∠APB=∠PBC-∠PAB=30°-15°=15°.
∴∠PAB=∠APB.
∴PB=AB=7 n mile.
∴PC=PB=×7=3.5 n mile.
∵PC<3.8 n mile,
∴该船一直向东航行有触礁的危险.
