13.4 课题学习 最短路径问题同步练习 (含答案)
文档属性
| 名称 | 13.4 课题学习 最短路径问题同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 19:52:45 | ||
图片预览




文档简介
13.4课题学习 最短路径问题
【知识重点】
知识点1 最短路径问题
1. 直线异侧的两点到直线上一点的距离的和最短的问题
如图,点A,B分别是直线l异侧的两个点,在直线l上找一点C,使CA+CB最小,这时点C就是线段AB与直线l的交点.
2. 直线同侧的两点到直线上一点的距离的和最短的问题
如图,点A,B分别是直线l同侧的两个点,在直线l上找一点C,使CA+CB最小,这时先作点B关于直线l的对称点B′,连接AB′交直线l于点C(也可以作点A关于直线l的对称点A′,连接A′B交直线l于点C),此时点C就是所求作的点.
特别解读
●直线异侧的两点到直线上一点的距离的和最短的问题是根据“两点之间,线段最短”来设计的.
●直线同侧的两点到直线上一点的距离的和最短的问题依据两点:一是对称轴上任何一点到一组对称点的距离相等;二是将同侧的两点转化为异侧的两点,依据异侧两点的方法找点.
知识点2 建桥选址问题
1. 解决“建桥选址”问题,一般用平移的方法,利用平移前后的对应线段相等,把未知的线段转换到一条直线上,再结合“两点之间,线段最短”解决问题.
2. 解决“建桥选址”问题的关键就是要通过平移桥,使除桥外的其他路径平移后在一条直线上.
特别解读
解决连接河两边两地的最短路径问题时,可以通过平移桥的方法转化为求直线异侧两点到直线上一点所连线段的和最小的问题.
【经典例题】
【例1】某供电部门准备在输电主干线l上连接一个分支线路,分支点为M,同时向新落成的A,B两个居民小区送电.
解题秘方:扣住两点是在直线同侧还是异侧两种类型解决.
(1)如果居民小区A,B在主干线l的两侧,如图,那么分支点M在什么地方时总线路最短?
(2)如果居民小区A,B在主干线l的同侧,如图13.4-4,那么分支点M在什么地方时总线路最短?
总结:解决“一线两点”型最短路径问题的方法
当两点在直线异侧时,连接两点,与直线的交点即为所求作的点;当两点在直线同侧时,作其中某一点关于直线的对称点,对称点与另一点的连线与直线的交点即为所求作的点.
【例2】如图,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边
b处饮水,最后回到营地. 请你设计一条放牧路线,使其所走的总路程最短.
解题秘方:要使其所走的总路程最短,可联想到“两点之间,线段最短”,因此需将三条线段转化到一条线段上,利用轴对称的性质进行转化.
总结:解决“两线一点”型最短路径问题的方法
分别以两线为对称轴,作已知点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例3】如图,山娃星期天从A处赶了几只羊到草地l1上吃草,然后赶羊到河边l2处饮水,
之后再回到B处的家. 假设山娃赶羊所走的路都是直路,请你为他设计一条最短的路线,并指明羊吃草与饮水的位置.
解题秘方:要使总路程最短,需要将三条线段想办法转化到一条线段上,可通过两次轴对称构造出最短路线.
总结:解决“两线两点”型最短路径问题的方法
以两线为对称轴,分别作靠近线的点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例4】如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
【同步练习】
一、选择题
1.如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B′;
②连接AB′,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( )
A.转化思想 B.三角形的两边之和大于第三边
C.两点之间,线段最短 D.三角形的一个外角大于与它不相邻的任意一个内角
2.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )
A. B.
C. D.
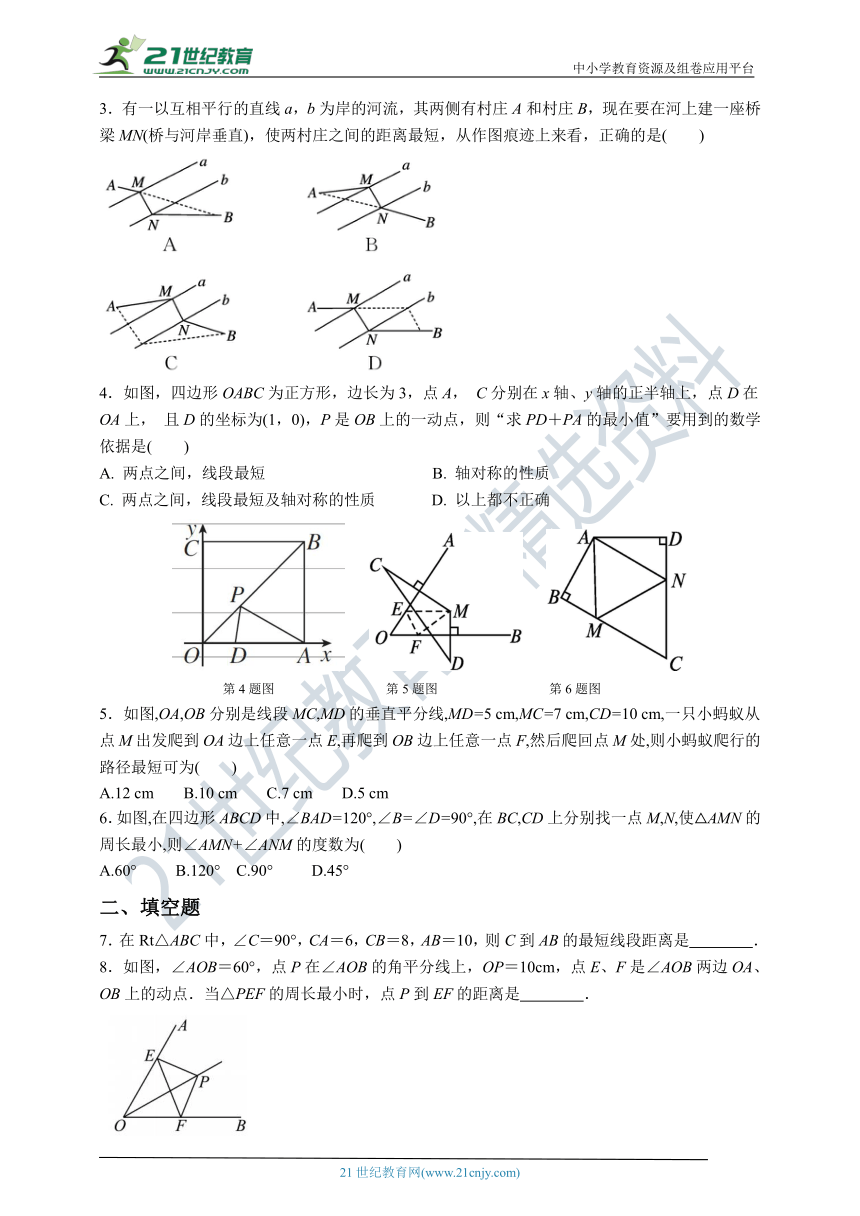
3.有一以互相平行的直线a,b为岸的河流,其两侧有村庄A和村庄B,现在要在河上建一座桥梁MN(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,正确的是( )
4.如图,四边形OABC为正方形,边长为3,点A, C分别在x轴、y轴的正半轴上,点D在OA上, 且D的坐标为(1,0),P是OB上的一动点,则“求PD+PA的最小值”要用到的数学依据是( )
A. 两点之间,线段最短 B. 轴对称的性质
C. 两点之间,线段最短及轴对称的性质 D. 以上都不正确
第4题图 第5题图 第6题图
5.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5 cm,MC=7 cm,CD=10 cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回点M处,则小蚂蚁爬行的路径最短可为( )
A.12 cm B.10 cm C.7 cm D.5 cm
6.如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )
A.60° B.120° C.90° D.45°
二、填空题
7.在Rt△ABC中,∠C=90°,CA=6,CB=8,AB=10,则C到AB的最短线段距离是 .
8.如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA、OB上的动点.当△PEF的周长最小时,点P到EF的距离是 .
三、解答题
9.如图,A、B在直线l同侧,在直线l上取一点P,使PA+PB最小.
10.如图,直线l1∥l2,A、B为两定点,M、N分别在直线l1、l2上,且MN⊥l2,请确定M、N的位置,使AM+MN+BN最小.
11.如图,某条护城河在CC′处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,恰当地造桥可使从A到B的路程最短,请确定两座桥的位置.
11.在一条河的同一岸上有A、B两个油库,要在河边修一个码头C,怎样作图使:
(1)A、B两油库到码头C的距离相等;
(2)AC+BC最短.
12.【2023·齐齐哈尔三中模拟】如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN的周长的最小值是5 cm,求∠AOB的度数.
13.如图,在公路l1、l2上要设两个变压供电站,由A村架设电线到B村再到两个供电站回到A村,则供电站M、N应设在公路l1、l2的何处才能使所用的电线最短?请画出l1、l2上供电站M、N的位置(不必说明理由).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】某供电部门准备在输电主干线l上连接一个分支线路,分支点为M,同时向新落成的A,B两个居民小区送电.
解题秘方:扣住两点是在直线同侧还是异侧两种类型解决.
(1)如果居民小区A,B在主干线l的两侧,如图13.4-3,那么分支点M在什么地方时总线路最短?
解:如图,连接AB,与l的交点即为所求的分支点M.
(2)如果居民小区A,B在主干线l的同侧,如图13.4-4,那么分支点M在什么地方时总线路最短?
解:如图,作点B关于l的对称点B1,连接AB1交l于点M,连接BM,此时AM+BM最短,则点M即为所求的分支点.
总结:解决“一线两点”型最短路径问题的方法
当两点在直线异侧时,连接两点,与直线的交点即为所求作的点;当两点在直线同侧时,作其中某一点关于直线的对称点,对称点与另一点的连线与直线的交点即为所求作的点.
【例2】如图,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边
b处饮水,最后回到营地. 请你设计一条放牧路线,使其所走的总路程最短.
解题秘方:要使其所走的总路程最短,可联想到“两点之间,线段最短”,因此需将三条线段转化到一条线段上,利用轴对称的性质进行转化.
解:如图13.4-5,作点P关于直线a的对称点P1,关于直线b的对称点P2,连接P1P2,分别交直线a,b于点A,B,连接PA,PB. 由轴对称的性质知,PA=P1A,PB=P2B,则先沿PA到点A处吃草,再沿AB到点B处饮水,最后沿BP回到营地,此时PA+AB+PB=P1A+AB+P2B=P1P2,按这样的路线放牧所走的总路程最短.
总结:解决“两线一点”型最短路径问题的方法
分别以两线为对称轴,作已知点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例3】如图,山娃星期天从A处赶了几只羊到草地l1上吃草,然后赶羊到河边l2处饮水,
之后再回到B处的家. 假设山娃赶羊所走的路都是直路,请你为他设计一条最短的路线,并指明羊吃草与饮水的位置.
解题秘方:要使总路程最短,需要将三条线段想办法转化到一条线段上,可通过两次轴对称构造出最短路线.
解:如图,作出点A关于l1的对称点E, 点B关于l2的对称点F, 连接EF,分别交l1,l2于点C,点D,连接AC,BD,则A → C → D →B是山娃所走的最短路线,其中点C是羊吃草的位置,点D是羊饮水的位置.
总结:解决“两线两点”型最短路径问题的方法
以两线为对称轴,分别作靠近线的点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例4】如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
提示:如图,从A到B要走的路线为A→M→N→B,因为河宽MN不变,所以要使路程最短,只要AM+BN最小即可;由平移MN到AC可知,连接B,C的线段长是AM+BN的最小值,此时BC与GH的交点N为桥的一端,MN就是所建的桥的位置.
解:(1)如图,过点A作AC垂直于河岸,且使AC等于河宽; (2)连接BC, 与河岸GH相交于点N,过点N作NM⊥EF于点M,则MN为所建桥的位置.
【同步练习】
一、选择题
1.如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B′;
②连接AB′,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( D )
A.转化思想 B.三角形的两边之和大于第三边
C.两点之间,线段最短 D.三角形的一个外角大于与它不相邻的任意一个内角
2.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( D )
A. B.
C. D.
3.有一以互相平行的直线a,b为岸的河流,其两侧有村庄A和村庄B,现在要在河上建一座桥梁MN(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,正确的是( D )
4.如图,四边形OABC为正方形,边长为3,点A, C分别在x轴、y轴的正半轴上,点D在OA上, 且D的坐标为(1,0),P是OB上的一动点,则“求PD+PA的最小值”要用到的数学依据是( C )
A. 两点之间,线段最短 B. 轴对称的性质
C. 两点之间,线段最短及轴对称的性质 D. 以上都不正确
第4题图 第5题图 第6题图
5.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5 cm,MC=7 cm,CD=10 cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回点M处,则小蚂蚁爬行的路径最短可为( B )
A.12 cm B.10 cm C.7 cm D.5 cm
6.如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( B )
A.60° B.120° C.90° D.45°
【答案】如图,作点A关于BC和CD的对称点A',A″,连接A'A″,交BC于点M,交CD于点N,则A'A″即为△AMN的周长的最小值.
∵∠DAB=120°,
∴∠A'+∠A″=180°-120°=60°.
∵∠A'=∠MAA',∠NAD=∠A″,
且∠A'+∠MAA'=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A'+∠MAA'+∠NAD+∠A″=2(∠A'+∠A″)=2×60°=120°,故选B.
二、填空题
7.在Rt△ABC中,∠C=90°,CA=6,CB=8,AB=10,则C到AB的最短线段距离是 .
【答案】4、8
8.如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA、OB上的动点.当△PEF的周长最小时,点P到EF的距离是 .
【答案】5 cm
三、解答题
9.如图,A、B在直线l同侧,在直线l上取一点P,使PA+PB最小.
解:作点A关于直线l的对称点A′,连接A′B交l于点P,则点P即为所求.
10.如图,直线l1∥l2,A、B为两定点,M、N分别在直线l1、l2上,且MN⊥l2,请确定M、N的位置,使AM+MN+BN最小.
解:过A作AA1⊥l1,且AA1=MN,连A1B,交l2于N,过N作MN⊥l2交l1于M,连AM,则AM+MN+BN最小.图略.
11.如图,某条护城河在CC′处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,恰当地造桥可使从A到B的路程最短,请确定两座桥的位置.
解:如图,作法如下:
(1)过点A作AF⊥CM,使AF等于河宽;过点B作BG⊥CN,使BG等于河宽;
(2)连接GF,分别与C′Q,C′P相交于点E′,D′;
(3)过点D′作D′D⊥CM于点D,过点E′作E′E⊥CN于点E,则D′D,E′E即为两座桥的位置.
11.在一条河的同一岸上有A、B两个油库,要在河边修一个码头C,怎样作图使:
(1)A、B两油库到码头C的距离相等;
(2)AC+BC最短.
解:(1)①连接AB,②作线段AB的垂直平分线MN交直线l于点C,则点C就是所求的点;
(2)①作点A关于l的对称点A′,②连接A′B交l于点C′,则C′为所求点.
12.【2023·齐齐哈尔三中模拟】如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN的周长的最小值是5 cm,求∠AOB的度数.
解:分别作点P关于射线OB,OA所在直线的对称点C,D,连接CD,分别交OA,OB于点M,N,连接OC,OD,PM,PN,如图所示.
∵点P关于射线OA所在直线的对称点为D,
∴PM=DM,OP=OD,∠DOA=∠POA.
∵点P关于射线OB所在直线的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB.
∴OC=OP=OD,∠AOB=∠COD.∵△PMN的周长的最小值是5 cm,
∴PM+PN+MN=5 cm.∴DM+CN+MN=5 cm,
即CD=5 cm=OP.∴OC=OD=CD,即△OCD是等边三角形.
∴∠COD=60°.∴∠AOB=30°.
13.如图,在公路l1、l2上要设两个变压供电站,由A村架设电线到B村再到两个供电站回到A村,则供电站M、N应设在公路l1、l2的何处才能使所用的电线最短?请画出l1、l2上供电站M、N的位置(不必说明理由).
解:如图,点M、N为所求.
【知识重点】
知识点1 最短路径问题
1. 直线异侧的两点到直线上一点的距离的和最短的问题
如图,点A,B分别是直线l异侧的两个点,在直线l上找一点C,使CA+CB最小,这时点C就是线段AB与直线l的交点.
2. 直线同侧的两点到直线上一点的距离的和最短的问题
如图,点A,B分别是直线l同侧的两个点,在直线l上找一点C,使CA+CB最小,这时先作点B关于直线l的对称点B′,连接AB′交直线l于点C(也可以作点A关于直线l的对称点A′,连接A′B交直线l于点C),此时点C就是所求作的点.
特别解读
●直线异侧的两点到直线上一点的距离的和最短的问题是根据“两点之间,线段最短”来设计的.
●直线同侧的两点到直线上一点的距离的和最短的问题依据两点:一是对称轴上任何一点到一组对称点的距离相等;二是将同侧的两点转化为异侧的两点,依据异侧两点的方法找点.
知识点2 建桥选址问题
1. 解决“建桥选址”问题,一般用平移的方法,利用平移前后的对应线段相等,把未知的线段转换到一条直线上,再结合“两点之间,线段最短”解决问题.
2. 解决“建桥选址”问题的关键就是要通过平移桥,使除桥外的其他路径平移后在一条直线上.
特别解读
解决连接河两边两地的最短路径问题时,可以通过平移桥的方法转化为求直线异侧两点到直线上一点所连线段的和最小的问题.
【经典例题】
【例1】某供电部门准备在输电主干线l上连接一个分支线路,分支点为M,同时向新落成的A,B两个居民小区送电.
解题秘方:扣住两点是在直线同侧还是异侧两种类型解决.
(1)如果居民小区A,B在主干线l的两侧,如图,那么分支点M在什么地方时总线路最短?
(2)如果居民小区A,B在主干线l的同侧,如图13.4-4,那么分支点M在什么地方时总线路最短?
总结:解决“一线两点”型最短路径问题的方法
当两点在直线异侧时,连接两点,与直线的交点即为所求作的点;当两点在直线同侧时,作其中某一点关于直线的对称点,对称点与另一点的连线与直线的交点即为所求作的点.
【例2】如图,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边
b处饮水,最后回到营地. 请你设计一条放牧路线,使其所走的总路程最短.
解题秘方:要使其所走的总路程最短,可联想到“两点之间,线段最短”,因此需将三条线段转化到一条线段上,利用轴对称的性质进行转化.
总结:解决“两线一点”型最短路径问题的方法
分别以两线为对称轴,作已知点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例3】如图,山娃星期天从A处赶了几只羊到草地l1上吃草,然后赶羊到河边l2处饮水,
之后再回到B处的家. 假设山娃赶羊所走的路都是直路,请你为他设计一条最短的路线,并指明羊吃草与饮水的位置.
解题秘方:要使总路程最短,需要将三条线段想办法转化到一条线段上,可通过两次轴对称构造出最短路线.
总结:解决“两线两点”型最短路径问题的方法
以两线为对称轴,分别作靠近线的点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例4】如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
【同步练习】
一、选择题
1.如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B′;
②连接AB′,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( )
A.转化思想 B.三角形的两边之和大于第三边
C.两点之间,线段最短 D.三角形的一个外角大于与它不相邻的任意一个内角
2.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )
A. B.
C. D.
3.有一以互相平行的直线a,b为岸的河流,其两侧有村庄A和村庄B,现在要在河上建一座桥梁MN(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,正确的是( )
4.如图,四边形OABC为正方形,边长为3,点A, C分别在x轴、y轴的正半轴上,点D在OA上, 且D的坐标为(1,0),P是OB上的一动点,则“求PD+PA的最小值”要用到的数学依据是( )
A. 两点之间,线段最短 B. 轴对称的性质
C. 两点之间,线段最短及轴对称的性质 D. 以上都不正确
第4题图 第5题图 第6题图
5.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5 cm,MC=7 cm,CD=10 cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回点M处,则小蚂蚁爬行的路径最短可为( )
A.12 cm B.10 cm C.7 cm D.5 cm
6.如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )
A.60° B.120° C.90° D.45°
二、填空题
7.在Rt△ABC中,∠C=90°,CA=6,CB=8,AB=10,则C到AB的最短线段距离是 .
8.如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA、OB上的动点.当△PEF的周长最小时,点P到EF的距离是 .
三、解答题
9.如图,A、B在直线l同侧,在直线l上取一点P,使PA+PB最小.
10.如图,直线l1∥l2,A、B为两定点,M、N分别在直线l1、l2上,且MN⊥l2,请确定M、N的位置,使AM+MN+BN最小.
11.如图,某条护城河在CC′处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,恰当地造桥可使从A到B的路程最短,请确定两座桥的位置.
11.在一条河的同一岸上有A、B两个油库,要在河边修一个码头C,怎样作图使:
(1)A、B两油库到码头C的距离相等;
(2)AC+BC最短.
12.【2023·齐齐哈尔三中模拟】如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN的周长的最小值是5 cm,求∠AOB的度数.
13.如图,在公路l1、l2上要设两个变压供电站,由A村架设电线到B村再到两个供电站回到A村,则供电站M、N应设在公路l1、l2的何处才能使所用的电线最短?请画出l1、l2上供电站M、N的位置(不必说明理由).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】某供电部门准备在输电主干线l上连接一个分支线路,分支点为M,同时向新落成的A,B两个居民小区送电.
解题秘方:扣住两点是在直线同侧还是异侧两种类型解决.
(1)如果居民小区A,B在主干线l的两侧,如图13.4-3,那么分支点M在什么地方时总线路最短?
解:如图,连接AB,与l的交点即为所求的分支点M.
(2)如果居民小区A,B在主干线l的同侧,如图13.4-4,那么分支点M在什么地方时总线路最短?
解:如图,作点B关于l的对称点B1,连接AB1交l于点M,连接BM,此时AM+BM最短,则点M即为所求的分支点.
总结:解决“一线两点”型最短路径问题的方法
当两点在直线异侧时,连接两点,与直线的交点即为所求作的点;当两点在直线同侧时,作其中某一点关于直线的对称点,对称点与另一点的连线与直线的交点即为所求作的点.
【例2】如图,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边
b处饮水,最后回到营地. 请你设计一条放牧路线,使其所走的总路程最短.
解题秘方:要使其所走的总路程最短,可联想到“两点之间,线段最短”,因此需将三条线段转化到一条线段上,利用轴对称的性质进行转化.
解:如图13.4-5,作点P关于直线a的对称点P1,关于直线b的对称点P2,连接P1P2,分别交直线a,b于点A,B,连接PA,PB. 由轴对称的性质知,PA=P1A,PB=P2B,则先沿PA到点A处吃草,再沿AB到点B处饮水,最后沿BP回到营地,此时PA+AB+PB=P1A+AB+P2B=P1P2,按这样的路线放牧所走的总路程最短.
总结:解决“两线一点”型最短路径问题的方法
分别以两线为对称轴,作已知点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例3】如图,山娃星期天从A处赶了几只羊到草地l1上吃草,然后赶羊到河边l2处饮水,
之后再回到B处的家. 假设山娃赶羊所走的路都是直路,请你为他设计一条最短的路线,并指明羊吃草与饮水的位置.
解题秘方:要使总路程最短,需要将三条线段想办法转化到一条线段上,可通过两次轴对称构造出最短路线.
解:如图,作出点A关于l1的对称点E, 点B关于l2的对称点F, 连接EF,分别交l1,l2于点C,点D,连接AC,BD,则A → C → D →B是山娃所走的最短路线,其中点C是羊吃草的位置,点D是羊饮水的位置.
总结:解决“两线两点”型最短路径问题的方法
以两线为对称轴,分别作靠近线的点的对称点,连接两个对称点,将最短路径转化为连接两个对称点的线段.
【例4】如图,从A地到B地要经过一条小河(河的两岸平行),现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从A地到B地的路程最短?
提示:如图,从A到B要走的路线为A→M→N→B,因为河宽MN不变,所以要使路程最短,只要AM+BN最小即可;由平移MN到AC可知,连接B,C的线段长是AM+BN的最小值,此时BC与GH的交点N为桥的一端,MN就是所建的桥的位置.
解:(1)如图,过点A作AC垂直于河岸,且使AC等于河宽; (2)连接BC, 与河岸GH相交于点N,过点N作NM⊥EF于点M,则MN为所建桥的位置.
【同步练习】
一、选择题
1.如图,直线l外不重合的两点A,B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:
①作点B关于直线l的对称点B′;
②连接AB′,与直线l相交于点C,则点C为所求作的点.
在解决这个问题时没有运用到的知识或方法是( D )
A.转化思想 B.三角形的两边之和大于第三边
C.两点之间,线段最短 D.三角形的一个外角大于与它不相邻的任意一个内角
2.如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( D )
A. B.
C. D.
3.有一以互相平行的直线a,b为岸的河流,其两侧有村庄A和村庄B,现在要在河上建一座桥梁MN(桥与河岸垂直),使两村庄之间的距离最短,从作图痕迹上来看,正确的是( D )
4.如图,四边形OABC为正方形,边长为3,点A, C分别在x轴、y轴的正半轴上,点D在OA上, 且D的坐标为(1,0),P是OB上的一动点,则“求PD+PA的最小值”要用到的数学依据是( C )
A. 两点之间,线段最短 B. 轴对称的性质
C. 两点之间,线段最短及轴对称的性质 D. 以上都不正确
第4题图 第5题图 第6题图
5.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5 cm,MC=7 cm,CD=10 cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回点M处,则小蚂蚁爬行的路径最短可为( B )
A.12 cm B.10 cm C.7 cm D.5 cm
6.如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( B )
A.60° B.120° C.90° D.45°
【答案】如图,作点A关于BC和CD的对称点A',A″,连接A'A″,交BC于点M,交CD于点N,则A'A″即为△AMN的周长的最小值.
∵∠DAB=120°,
∴∠A'+∠A″=180°-120°=60°.
∵∠A'=∠MAA',∠NAD=∠A″,
且∠A'+∠MAA'=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A'+∠MAA'+∠NAD+∠A″=2(∠A'+∠A″)=2×60°=120°,故选B.
二、填空题
7.在Rt△ABC中,∠C=90°,CA=6,CB=8,AB=10,则C到AB的最短线段距离是 .
【答案】4、8
8.如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA、OB上的动点.当△PEF的周长最小时,点P到EF的距离是 .
【答案】5 cm
三、解答题
9.如图,A、B在直线l同侧,在直线l上取一点P,使PA+PB最小.
解:作点A关于直线l的对称点A′,连接A′B交l于点P,则点P即为所求.
10.如图,直线l1∥l2,A、B为两定点,M、N分别在直线l1、l2上,且MN⊥l2,请确定M、N的位置,使AM+MN+BN最小.
解:过A作AA1⊥l1,且AA1=MN,连A1B,交l2于N,过N作MN⊥l2交l1于M,连AM,则AM+MN+BN最小.图略.
11.如图,某条护城河在CC′处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,恰当地造桥可使从A到B的路程最短,请确定两座桥的位置.
解:如图,作法如下:
(1)过点A作AF⊥CM,使AF等于河宽;过点B作BG⊥CN,使BG等于河宽;
(2)连接GF,分别与C′Q,C′P相交于点E′,D′;
(3)过点D′作D′D⊥CM于点D,过点E′作E′E⊥CN于点E,则D′D,E′E即为两座桥的位置.
11.在一条河的同一岸上有A、B两个油库,要在河边修一个码头C,怎样作图使:
(1)A、B两油库到码头C的距离相等;
(2)AC+BC最短.
解:(1)①连接AB,②作线段AB的垂直平分线MN交直线l于点C,则点C就是所求的点;
(2)①作点A关于l的对称点A′,②连接A′B交l于点C′,则C′为所求点.
12.【2023·齐齐哈尔三中模拟】如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN的周长的最小值是5 cm,求∠AOB的度数.
解:分别作点P关于射线OB,OA所在直线的对称点C,D,连接CD,分别交OA,OB于点M,N,连接OC,OD,PM,PN,如图所示.
∵点P关于射线OA所在直线的对称点为D,
∴PM=DM,OP=OD,∠DOA=∠POA.
∵点P关于射线OB所在直线的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB.
∴OC=OP=OD,∠AOB=∠COD.∵△PMN的周长的最小值是5 cm,
∴PM+PN+MN=5 cm.∴DM+CN+MN=5 cm,
即CD=5 cm=OP.∴OC=OD=CD,即△OCD是等边三角形.
∴∠COD=60°.∴∠AOB=30°.
13.如图,在公路l1、l2上要设两个变压供电站,由A村架设电线到B村再到两个供电站回到A村,则供电站M、N应设在公路l1、l2的何处才能使所用的电线最短?请画出l1、l2上供电站M、N的位置(不必说明理由).
解:如图,点M、N为所求.
