19.2.1正比例函数1课件
文档属性
| 名称 | 19.2.1正比例函数1课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-08 00:00:00 | ||
图片预览








文档简介
课件22张PPT。§19.2.1 正比例函数(一)学习目标1.掌握正比例函数的概念.
2.弄清正比例函数解析式中字母的意义.
3.会求正比例函数的解析式.自学指导阅读课本P110—111 页思考以下问题:
1.思考并解决110页的问题.
2.阅读并解决111页思考所提出的问题.
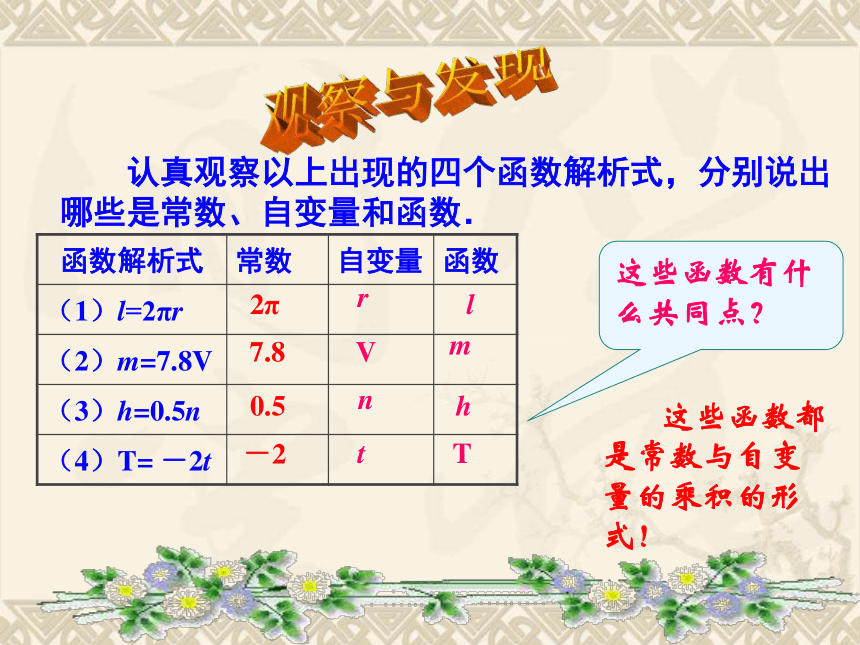
3.观察所列的解析式有什么共同特征? 问题:1996年,鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在25600千米外的澳大利亚发现了它。 问题研讨(1)这只百余克重的小鸟大约平均每天飞行多少千米?(2)这只燕鸥的行程y(单位:千米)与飞行的时间x(单位:天)之间有什么关系?25600÷128=200(km)y=200x (0≤x≤128)(3)这只燕鸥飞行1个半月(一个月按30天计算)的行程大约是多少千米?当x=45时,y=200×45=9000 下列问题中的变量对应规律可用怎样的函数表示?这些函数有什么共同点?开动脑筋(1)圆的周长L随半径r 大小变化而变化;L=2πrm=7.8V(2)铁的密度为7.8g/ ,铁块的质量m(单位g)随它的体积V(单位 )大小变化而变化;开动脑筋(4)冷冻一个0℃物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化。 下列问题中的变量对应规律可用怎样的函数表示?这些函数有什么共同点?(3)每个练习本的厚度为0.5cm,一些练习本撂在一起的总厚度h(单位cm)随这些练习本的本数n的变化而变化;h=0.5nT=-2t观察与发现 认真观察以上出现的四个函数解析式,分别说出哪些是常数、自变量和函数.这些函数有什么共同点? 这些函数都是常数与自变量的乘积的形式! 2πrl 7.8Vm 0.5nh -2tT归纳与总结 一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.勤学
好问这里为什么强调k是常数, k≠0呢?下列函数是否是正比例函数?比例系数是多少?是,比例系数k=3.不是.是,比例系数k= 你能举出一些正比例函数的例子吗?S 不是r的正比例函数,S是的正比例函数.试一试必做题判断下列各题中所指的两个量是否成正比例。
(是在括号内打“ ” ,不是在括号内打“ ”)(1)圆周长C与半径r( )
(2)圆面积S与半径r ( )
(3)在匀速运动中的路
程S与时间t ( )
(4)底面半径r为定长的圆锥的侧
面积S与母线长l( )
(5)已知y=3x-2,y与x ( )
S = v t例:已知y与x成正比例,当x=4时,y=8,试求y与x的函数解析式解:∵y与x成正比例∴y=kx又∵当x=4时,y=8∴8=4k∴k=2∴y与x的函数解析式为:y=2x 正比例函数y=kx中,当x=2时,
y=10,则它的解析式是_________. 若一个正比例函数的比例系数是4,
则它的解析式是__________.y = 4xy = 5x必做题已知正比例函数y=2x中,
(1)若0< y <10,则x的取值范围为_________.
(2)若-6< x <10,则y的取值范围为_________.0< <10-6< <100(1)写出△ABC的面积y(cm2)与高线x的函数解析式,并指明它是什么函数;
(2)当x=7时,求出y的值。解: (1)(2)当x=7时,y=4×7=28例3 已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。解:∵ y与x-1成正比例 ∴y=k(x-1)
∵ 当x=8时,y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是:当x=4时 当x=-3时 已知y与x+2 成正比例,当x=4时,y=12,那么当x=5时,y=______.解:∵ y与x+2 成正比例∴y=k(x+2)∵当x=4时,y=12∴12=k(4+2)解得:k=2∴y=2x+4∴当x=5时,y=1414必做题 已知y=y1+y2,y1与x2成正比例,y2与x-2成正比例,当x=1时,y=0,当x=-3时,y=4,求x=3时,y的值。选做题 某学校准备添置一批篮球,已知所购篮球的总价y(元)与个数x(个)成正比例,当x=4(个)时,y=100(元)。
(1)求正比例函数关系式及自变量的取值范围;
(2)求当x=10(个)时,函数y的值;
(3)求当y=500(元)时,自变量x的值。解(1)设所求的正比例函数的解析式为y=kx,(2)当x=10(个)时,y=25x=25×10=250(元)。∵当x =4时,y =100,∴100=4k。解得 k= 25。∴所求正比例函数的解析式是y=25x。自变量x的取值范围是所有自然数。 1.下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米 下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米解(1)设所求的正比例函数的解析式为S=k t,(2)由已知得30≤t≤40,把t =4,S =2代入,得 2=4t。解得 k= 0.5 。所以,所求的正比例函数的解析式是S=0.5t。∴ 30≤2S≤40即15 ≤S≤20。由图可知中巴车行使在贺村至淤头公路上。(3)由已知得20≤S≤22,∴ 20≤0.5t≤22即40≤t≤44。所以从8:40至8:44,该车行使在淤头至礼贤公路上。 2、周末马老师提着篮子(篮子重0.5斤)到菜场买10斤鸡蛋,当马老师往篮子里捡称好的鸡蛋时,发觉比过去买10斤鸡蛋时个数少很多,于是他将鸡蛋装进篮子里再让摊主一起称,共10.55斤,即刻他要求摊主退一斤鸡蛋的钱,他是怎样知道摊主少称了大约1斤鸡蛋的呢?你能知道其中的原因吗?本课小结函数y= kx(k是不等于零的常数)叫做正比例函数。 (1)直接根据已知的比例系数求出解析式
(2)待定系数法1、正比例函数的定义2、求正比例函数解析式的两种方法:3、在知道正比例函数解析式的前提下函数的值与取值范围自变量的值与取值范围再见
2.弄清正比例函数解析式中字母的意义.
3.会求正比例函数的解析式.自学指导阅读课本P110—111 页思考以下问题:
1.思考并解决110页的问题.
2.阅读并解决111页思考所提出的问题.
3.观察所列的解析式有什么共同特征? 问题:1996年,鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在25600千米外的澳大利亚发现了它。 问题研讨(1)这只百余克重的小鸟大约平均每天飞行多少千米?(2)这只燕鸥的行程y(单位:千米)与飞行的时间x(单位:天)之间有什么关系?25600÷128=200(km)y=200x (0≤x≤128)(3)这只燕鸥飞行1个半月(一个月按30天计算)的行程大约是多少千米?当x=45时,y=200×45=9000 下列问题中的变量对应规律可用怎样的函数表示?这些函数有什么共同点?开动脑筋(1)圆的周长L随半径r 大小变化而变化;L=2πrm=7.8V(2)铁的密度为7.8g/ ,铁块的质量m(单位g)随它的体积V(单位 )大小变化而变化;开动脑筋(4)冷冻一个0℃物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)的变化而变化。 下列问题中的变量对应规律可用怎样的函数表示?这些函数有什么共同点?(3)每个练习本的厚度为0.5cm,一些练习本撂在一起的总厚度h(单位cm)随这些练习本的本数n的变化而变化;h=0.5nT=-2t观察与发现 认真观察以上出现的四个函数解析式,分别说出哪些是常数、自变量和函数.这些函数有什么共同点? 这些函数都是常数与自变量的乘积的形式! 2πrl 7.8Vm 0.5nh -2tT归纳与总结 一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.勤学
好问这里为什么强调k是常数, k≠0呢?下列函数是否是正比例函数?比例系数是多少?是,比例系数k=3.不是.是,比例系数k= 你能举出一些正比例函数的例子吗?S 不是r的正比例函数,S是的正比例函数.试一试必做题判断下列各题中所指的两个量是否成正比例。
(是在括号内打“ ” ,不是在括号内打“ ”)(1)圆周长C与半径r( )
(2)圆面积S与半径r ( )
(3)在匀速运动中的路
程S与时间t ( )
(4)底面半径r为定长的圆锥的侧
面积S与母线长l( )
(5)已知y=3x-2,y与x ( )
S = v t例:已知y与x成正比例,当x=4时,y=8,试求y与x的函数解析式解:∵y与x成正比例∴y=kx又∵当x=4时,y=8∴8=4k∴k=2∴y与x的函数解析式为:y=2x 正比例函数y=kx中,当x=2时,
y=10,则它的解析式是_________. 若一个正比例函数的比例系数是4,
则它的解析式是__________.y = 4xy = 5x必做题已知正比例函数y=2x中,
(1)若0< y <10,则x的取值范围为_________.
(2)若-6< x <10,则y的取值范围为_________.0< <10-6< <100
(2)当x=7时,求出y的值。解: (1)(2)当x=7时,y=4×7=28例3 已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。解:∵ y与x-1成正比例 ∴y=k(x-1)
∵ 当x=8时,y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是:当x=4时 当x=-3时 已知y与x+2 成正比例,当x=4时,y=12,那么当x=5时,y=______.解:∵ y与x+2 成正比例∴y=k(x+2)∵当x=4时,y=12∴12=k(4+2)解得:k=2∴y=2x+4∴当x=5时,y=1414必做题 已知y=y1+y2,y1与x2成正比例,y2与x-2成正比例,当x=1时,y=0,当x=-3时,y=4,求x=3时,y的值。选做题 某学校准备添置一批篮球,已知所购篮球的总价y(元)与个数x(个)成正比例,当x=4(个)时,y=100(元)。
(1)求正比例函数关系式及自变量的取值范围;
(2)求当x=10(个)时,函数y的值;
(3)求当y=500(元)时,自变量x的值。解(1)设所求的正比例函数的解析式为y=kx,(2)当x=10(个)时,y=25x=25×10=250(元)。∵当x =4时,y =100,∴100=4k。解得 k= 25。∴所求正比例函数的解析式是y=25x。自变量x的取值范围是所有自然数。 1.下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米 下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米解(1)设所求的正比例函数的解析式为S=k t,(2)由已知得30≤t≤40,把t =4,S =2代入,得 2=4t。解得 k= 0.5 。所以,所求的正比例函数的解析式是S=0.5t。∴ 30≤2S≤40即15 ≤S≤20。由图可知中巴车行使在贺村至淤头公路上。(3)由已知得20≤S≤22,∴ 20≤0.5t≤22即40≤t≤44。所以从8:40至8:44,该车行使在淤头至礼贤公路上。 2、周末马老师提着篮子(篮子重0.5斤)到菜场买10斤鸡蛋,当马老师往篮子里捡称好的鸡蛋时,发觉比过去买10斤鸡蛋时个数少很多,于是他将鸡蛋装进篮子里再让摊主一起称,共10.55斤,即刻他要求摊主退一斤鸡蛋的钱,他是怎样知道摊主少称了大约1斤鸡蛋的呢?你能知道其中的原因吗?本课小结函数y= kx(k是不等于零的常数)叫做正比例函数。 (1)直接根据已知的比例系数求出解析式
(2)待定系数法1、正比例函数的定义2、求正比例函数解析式的两种方法:3、在知道正比例函数解析式的前提下函数的值与取值范围自变量的值与取值范围再见
