14.1.1 同底数幂的乘法 课件(共26张PPT)
文档属性
| 名称 | 14.1.1 同底数幂的乘法 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 21:05:29 | ||
图片预览








文档简介
(共26张PPT)
14.1 整式的乘法
第十四章 整式的乘法与因式分解
14.1.1 同底数幂的乘法
学习目标
1.理解同底数幂的乘法法则.
2.会运用同底数幂的乘法法则进行计算.
3.会运用同底数幂的乘法法则解决一些实际问题.
重点:同底数幂的乘法计算法则及公式.
难点:运用公式.
课前预习
阅读课本P95-96页内容,了解本节主要内容.
底数
a的n次幂
指数
不变
相加
am+n
am· an
新课导入
国家并行计算机工程技术研究中心研制的某款超级计算机每秒运算速度超过十亿亿次(1017 次)的超级计算机.请问它工作 103 s 可进行多少次运算?
同底数幂相乘
一
互动探究
该超级计算机每秒运算速度超过十亿亿次(1017次).请问它工作103s可进行多少次运算?
问题1 怎样列式?
1017 ×103
新知探究
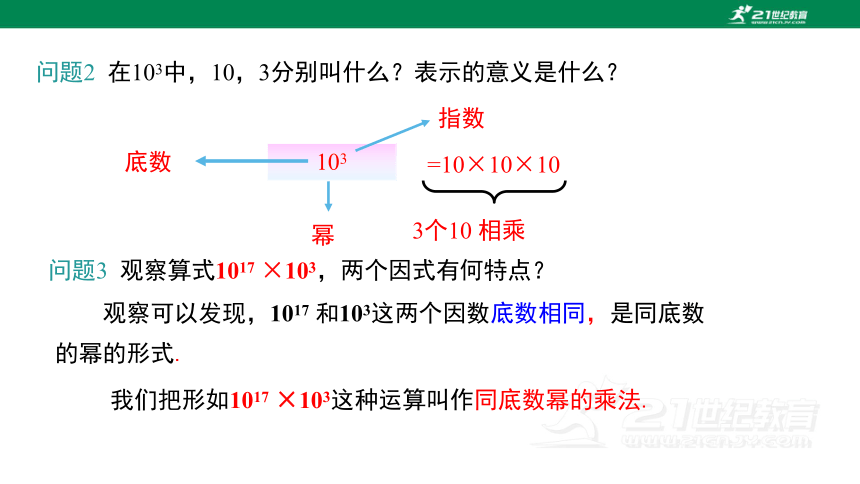
问题2 在103中,10,3分别叫什么?表示的意义是什么?
=10×10×10
3个10 相乘
103
底数
幂
指数
问题3 观察算式1017 ×103,两个因式有何特点?
观察可以发现,1017 和103这两个因数底数相同,是同底数的幂的形式.
我们把形如1017 ×103这种运算叫作同底数幂的乘法.
问题4 根据乘方的意义,想一想如何计算1017 ×103?
=(10×10×10 ×…×10)
17个10
×(10×10×10)
3个10
=10×10×…×10
20个10
=1020
=1017+3
(乘方的意义)
(乘法的结合律)
(乘方的意义)
1017×103
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
试一试
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2× 2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
同底数幂相乘,底数不变,指数相加
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
猜一猜
am · an =a( )
m+n
注意观察:计算前后,底数和指数有何变化
am·an
=(a·a·…a)
( 个a)
(a·a·…a)
( 个a)
=(a·a·…a)
( __ 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+ n
m+n
证一证
·
am · an = am+n (m、n都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加.
同底数幂的乘法法则:
要点归纳
结果:①底数不变
②指数相加
注意
条件:①乘法
②底数相同
(1) 105×106=_____________;
(2) a7 ·a3=_____________;
(3) x5 ·x7=_____________;
练一练
计算:
(4) (-b)3 ·(-b)2=_____________.
1011
a10
x12
(-b)5
=-b5
a · a6 · a3
类比同底数幂的乘法公式
am · an = am+n (m、n都是正整数)
am· an· ap = am+n+p (m、n、p都是正整数)
想一想: 当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
比一比
= a7 · a3 =a10
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
×
×
×
×
b6
2b3
=x8
a9
(-x)8
练一练
例1 计算:
(1)x2 · x5 ;
(2)a · a6;
(3)(-2) × (-2)4 × (-2)3;
(4) xm · x3m+1.
解:(1) x2 · x5= x2+5 =x7
(2)a · a6= a1+6 = a7;
(3)(-2) × (-2)4 × (-2)3= (-2) 1+4+3 = (-2)8 = 256;
(4) xm · x3m+1= xm+3m+1 = x4m+1.
a=a1
典例分析
例2 计算:
(1)(a+b)4 · (a+b)7 ;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 ;
(3)(x-y)2·(y-x)5.
解:(1) (a+b)4 · (a+b)7 = (a+b)4+7 =(a+b)11;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 =(m-n)3+5+7=(m-n)15;
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5
=(y-x)2+5=(y-x)7.
方法总结:公式am · an = am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.当底数互为相反数的幂相乘时,先把底数统一,再进行计算.
n为偶数
n为奇数
想一想:am+n可以写成哪两个因式的积?
同底数幂乘法法则的逆用
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
例3 (1)若xa=3,xb=4,xc=5,求2xa+b+c的值.
(2)已知23x+2=32,求x的值;
(2) ∵ 23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1) 2xa+b+c=2xa·xb·xc=120.
方法总结:(1)关键是逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
1.下列各式的结果等于26的是( )
A 2+25 B 2·25
C 23·25 D 0.22· 0.24
B
2.下列计算结果正确的是( )
A a3 · a3=a9 B m2 · n2=mn4
C xm · x3=x3m D y · yn=yn+1
D
随堂练习
(1)x·x2·x( )=x7; (2)xm·( )=x3m;
(3)8×4=2x,则x=( ).
4
5
x2m
4.填空:
3.计算:
(1) xn+1·x2n=_______;
(2) (a-b)2·(a-b)3=_______;
(3) -a4·(-a)2=_______;
(4) y4·y3·y2·y =_______.
x3n+1
(a-b)5
-a6
y10
5.计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)3·(b-a)4;
(3) (-3)×(-3)2 ×(-3)3;
(1)(2a+b)2n+1·(2a+b)3;
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3) (-3)×(-3)2 ×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
(2)已知an-3·a2n+1=a10,求n的值;
解:n-3+2n+1=10,
n=4;
6.(1)已知xa=8,xb=9,求xa+b的值;
解:xa+b=xa·xb
=8×9=72;
(3) 3×27×9 = 32x-4,求x的值;
解:3×27×9 =3×33×32=32x-4,
2x-4=6;
x=5.
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
课堂小结
本课结束
*
*
14.1 整式的乘法
第十四章 整式的乘法与因式分解
14.1.1 同底数幂的乘法
学习目标
1.理解同底数幂的乘法法则.
2.会运用同底数幂的乘法法则进行计算.
3.会运用同底数幂的乘法法则解决一些实际问题.
重点:同底数幂的乘法计算法则及公式.
难点:运用公式.
课前预习
阅读课本P95-96页内容,了解本节主要内容.
底数
a的n次幂
指数
不变
相加
am+n
am· an
新课导入
国家并行计算机工程技术研究中心研制的某款超级计算机每秒运算速度超过十亿亿次(1017 次)的超级计算机.请问它工作 103 s 可进行多少次运算?
同底数幂相乘
一
互动探究
该超级计算机每秒运算速度超过十亿亿次(1017次).请问它工作103s可进行多少次运算?
问题1 怎样列式?
1017 ×103
新知探究
问题2 在103中,10,3分别叫什么?表示的意义是什么?
=10×10×10
3个10 相乘
103
底数
幂
指数
问题3 观察算式1017 ×103,两个因式有何特点?
观察可以发现,1017 和103这两个因数底数相同,是同底数的幂的形式.
我们把形如1017 ×103这种运算叫作同底数幂的乘法.
问题4 根据乘方的意义,想一想如何计算1017 ×103?
=(10×10×10 ×…×10)
17个10
×(10×10×10)
3个10
=10×10×…×10
20个10
=1020
=1017+3
(乘方的意义)
(乘法的结合律)
(乘方的意义)
1017×103
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
试一试
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2× 2×2
=27
(2)a3·a2=a( )
=(a﹒a﹒a) (a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
同底数幂相乘,底数不变,指数相加
(3)5m× 5n =5( )
=(5×5×5×…×5)
m个5
×(5×5×5 ×…×5)
n个5
=5×5×…×5
(m+n)个5
=5m+n
猜一猜
am · an =a( )
m+n
注意观察:计算前后,底数和指数有何变化
am·an
=(a·a·…a)
( 个a)
(a·a·…a)
( 个a)
=(a·a·…a)
( __ 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+ n
m+n
证一证
·
am · an = am+n (m、n都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加.
同底数幂的乘法法则:
要点归纳
结果:①底数不变
②指数相加
注意
条件:①乘法
②底数相同
(1) 105×106=_____________;
(2) a7 ·a3=_____________;
(3) x5 ·x7=_____________;
练一练
计算:
(4) (-b)3 ·(-b)2=_____________.
1011
a10
x12
(-b)5
=-b5
a · a6 · a3
类比同底数幂的乘法公式
am · an = am+n (m、n都是正整数)
am· an· ap = am+n+p (m、n、p都是正整数)
想一想: 当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
比一比
= a7 · a3 =a10
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
×
×
×
×
b6
2b3
=x8
a9
(-x)8
练一练
例1 计算:
(1)x2 · x5 ;
(2)a · a6;
(3)(-2) × (-2)4 × (-2)3;
(4) xm · x3m+1.
解:(1) x2 · x5= x2+5 =x7
(2)a · a6= a1+6 = a7;
(3)(-2) × (-2)4 × (-2)3= (-2) 1+4+3 = (-2)8 = 256;
(4) xm · x3m+1= xm+3m+1 = x4m+1.
a=a1
典例分析
例2 计算:
(1)(a+b)4 · (a+b)7 ;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 ;
(3)(x-y)2·(y-x)5.
解:(1) (a+b)4 · (a+b)7 = (a+b)4+7 =(a+b)11;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 =(m-n)3+5+7=(m-n)15;
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5
=(y-x)2+5=(y-x)7.
方法总结:公式am · an = am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.当底数互为相反数的幂相乘时,先把底数统一,再进行计算.
n为偶数
n为奇数
想一想:am+n可以写成哪两个因式的积?
同底数幂乘法法则的逆用
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
例3 (1)若xa=3,xb=4,xc=5,求2xa+b+c的值.
(2)已知23x+2=32,求x的值;
(2) ∵ 23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1) 2xa+b+c=2xa·xb·xc=120.
方法总结:(1)关键是逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
1.下列各式的结果等于26的是( )
A 2+25 B 2·25
C 23·25 D 0.22· 0.24
B
2.下列计算结果正确的是( )
A a3 · a3=a9 B m2 · n2=mn4
C xm · x3=x3m D y · yn=yn+1
D
随堂练习
(1)x·x2·x( )=x7; (2)xm·( )=x3m;
(3)8×4=2x,则x=( ).
4
5
x2m
4.填空:
3.计算:
(1) xn+1·x2n=_______;
(2) (a-b)2·(a-b)3=_______;
(3) -a4·(-a)2=_______;
(4) y4·y3·y2·y =_______.
x3n+1
(a-b)5
-a6
y10
5.计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)3·(b-a)4;
(3) (-3)×(-3)2 ×(-3)3;
(1)(2a+b)2n+1·(2a+b)3;
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3) (-3)×(-3)2 ×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
(2)已知an-3·a2n+1=a10,求n的值;
解:n-3+2n+1=10,
n=4;
6.(1)已知xa=8,xb=9,求xa+b的值;
解:xa+b=xa·xb
=8×9=72;
(3) 3×27×9 = 32x-4,求x的值;
解:3×27×9 =3×33×32=32x-4,
2x-4=6;
x=5.
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
课堂小结
本课结束
*
*
