2015春湘教版数学八下第四章《一次函数》全章导学案
文档属性
| 名称 | 2015春湘教版数学八下第四章《一次函数》全章导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 869.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-08 00:00:00 | ||
图片预览


文档简介
4.1.1变量与函数
【学习目标】
1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;
2、学会用含一个变量的代数式表示另一个变量;
3、结合实例,理解函数的概念以及自变量的意义;在理解掌握函数概念的基础上,确定函数关系式;
4、会根据函数解析式和实际意义确定自变量的取值范围。
【学习重点】了解常量与变量的意义;理解函数概念和自变量的意义;确定函数关系式。
【学习难点】函数概念的理解;函数关系式的确定
学习过程:
一、【知识链接】
问题一:一辆汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.
1.请同学们根据题意填写下表:
t/时 1 2 3 4 5 t
s/千米
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含t的式子表示s.__s=_________________t的取值范围是
这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
二、【自主学习】
问题二:每张电影票的售价为10元,如果早 ( http: / / www.21cnjy.com )场售出票150张,午场售出205张,晚场售出310张,三场电影的票房收入各多少元?设一场电影售票x张,票房收入y元.怎样用含x的式子表示y
1.请同学们根据题意填写下表:
售出票数(张) 早场150 午场206 晚场310 x
收入y (元)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示y.__y=_________________x的取值范围是
这个问题反映了票房收入_________随售票张数_________的变化过程.
问题三:在一根弹簧的下端悬挂重物,改变并记 ( http: / / www.21cnjy.com )录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律.如果弹簧原长10cm,每1kg重物使弹簧伸长0.5cm,设重物质量为mkg,受力后的弹簧长度为L cm,怎样用含m的式子表示L?
1.请同学们根据题意填写下表:
所挂重物(kg) 1 2 3 4 5 m
受力后的弹簧长度L(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含m的式子表示L.__L=_________________m的取值范围是
这个问题反映了_________随_________的变化过程.
三、【合作探究】
问题四:圆的面积和它的半径之间的关系是什么 ( http: / / www.21cnjy.com )?要画一个面积为10cm2的圆,圆的半径应取多少?圆的面积为20cm2呢?30 cm2呢 怎样用含有圆面积S的式子表示圆半径r? 关系式:________
1.请同学们根据题意填写下表:
面积s(cm2) 10 20 30 s
半径r(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含s的式子表示r.__r=_________________s的取值范围是
这个问题反映了___ _ 随_ __的变化过程.
问题五:用10m长的绳子围 ( http: / / www.21cnjy.com )成矩形,试改变矩形的长度,观察矩形的面积怎样变化.记录不同的矩形的长度值,计算相应的矩形面积的值,探索它们的变化规律。设矩形的长为xm,面积为Sm2,怎样用含有x的式子表示S呢?
1.请同学们根据题意填写下表:
长x(m) 1 2 3 4 x
面积s(m2)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示s. _______________x的取值范围是
这个问题反映了矩形的___ _ 随_ __的变化过程.
四、【展示交流】
小结:以上这些问题都反映了不同事物的变 ( http: / / www.21cnjy.com )化过程,其实现实生活中还有好多类似的问题,在这些变化过程中,有些量的值是按照某种规律变化的(如……),有些量的数值是始终不变的(如……)。
得出结论: 在一个变化过程中,我们称数值发生变化的量为________;
在一个变化过程中,我们称数值始终不变的量为________;
(一)观察探究:
1、在前面研究的每个问题中,都出现了______个变量,它们之间是相互影响,相互制约的.
2、同一个问题中的变量之间有什么联 ( http: / / www.21cnjy.com )系?(请同学们自己分析“问题一”中两个变量之间的关系,进而再分析上述所有实例中的两个变量之间是否有类似的关系.)
归纳:上面每个问题中的两个变量相互联系,当其中一个变量取定一个值时,另一个变量就有________确定的值与其对应。
3、其实,在一些用图或表格表达的问题中,也能看到两个变量间有上述这样的关系.我们来看下面两个问题,通过观察、思考、讨论后回答:
(1)下图是体检时的心电图.其中图 ( http: / / www.21cnjy.com )上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
( http: / / www.21cnjy.com )
(2)在下面的我国人口数统计表中,年份与人口 ( http: / / www.21cnjy.com )数可以记作两个变量x与y,对于表中每一个确定的年份(x),都对应着一个确定的人口数(y)吗?中国人口数统计表
(二)归纳概念:
一般地,在一个变化过程 ( http: / / www.21cnjy.com )中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是_________,y是x的________.如果当x=a时y=b,那么b叫做当自变量的值为a时的_________.
举例说明:
问题一 问题二 问题三 问题四 问题五
自变量
自变量的函数
函数解析式
五、【当堂检测】
1、若球体体积为V,半径为R,则V=R3.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,R的取值范围是
2、校园里栽下一棵小树高 ( http: / / www.21cnjy.com )1.8米,以后每年长0.3米,则n年后的树高L与年数n之间的函数关系式__________.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,n的取值范围是
3、在男子1500米赛跑中,运动员的平 ( http: / / www.21cnjy.com )均速度v= ,则这个关系式中变量是_______、_______,常量是________.自变量是 , 是 的函数,自变量的取值范围是
4、已知2x-3y=1,若把y看成x的 ( http: / / www.21cnjy.com )函数,则可以表示为___________.其中变量是_____、_____,常量是________.自变量是 , 是 的函数,x的取值范围是
六、【学后反思】
4.1.2函数的图象(一)
【学习目标】
会观察函数图象,从函数图像中获取信息,解决问题。
【学习重难点】
初步掌握画函数图象的方法;通过观察、分析函数图象来获取信息.
一、【知识链接】
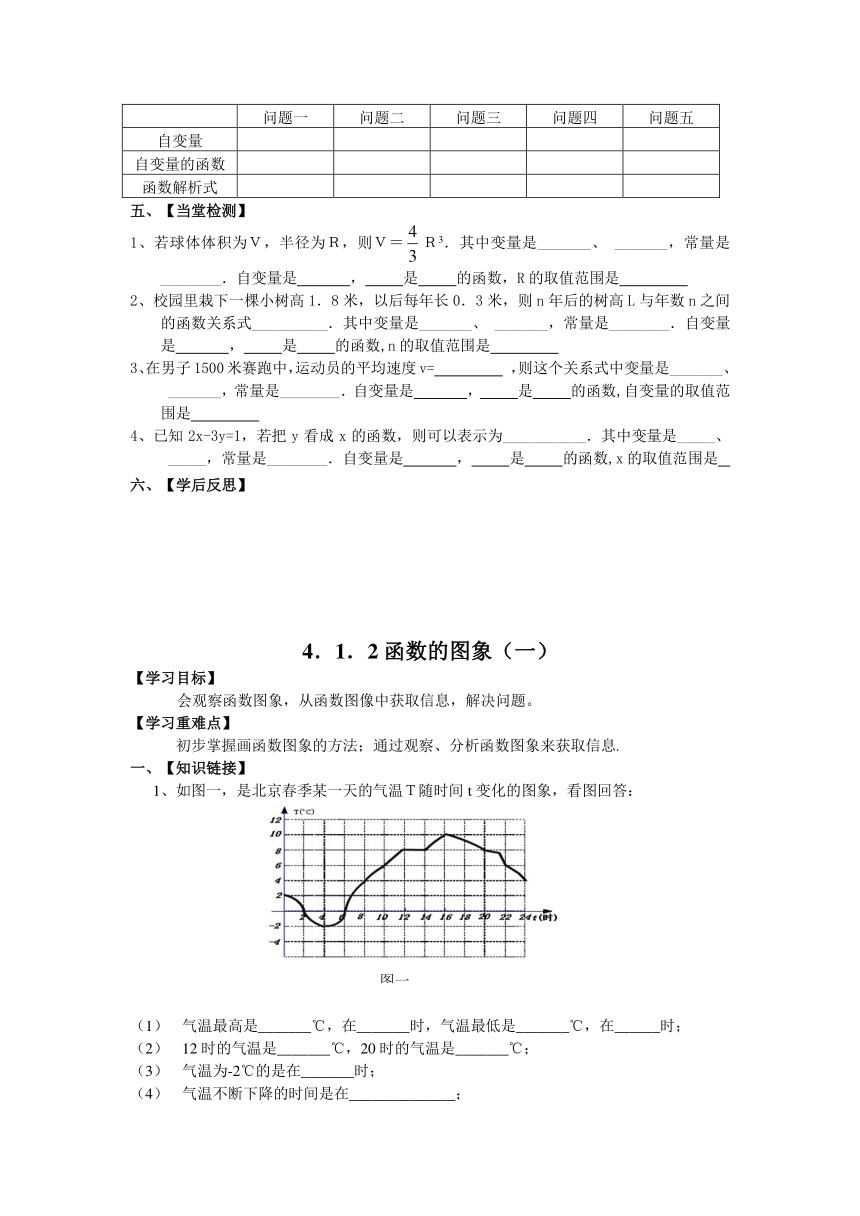
1、如图一,是北京春季某一天的气温T随时间t变化的图象,看图回答:
气温最高是_______℃,在_______时,气温最低是_______℃,在______时;
12时的气温是_______℃,20时的气温是_______℃;
气温为-2℃的是在_______时;
气温不断下降的时间是在______________;
气温持续不变的时间是在______________。
二、【自主学习】
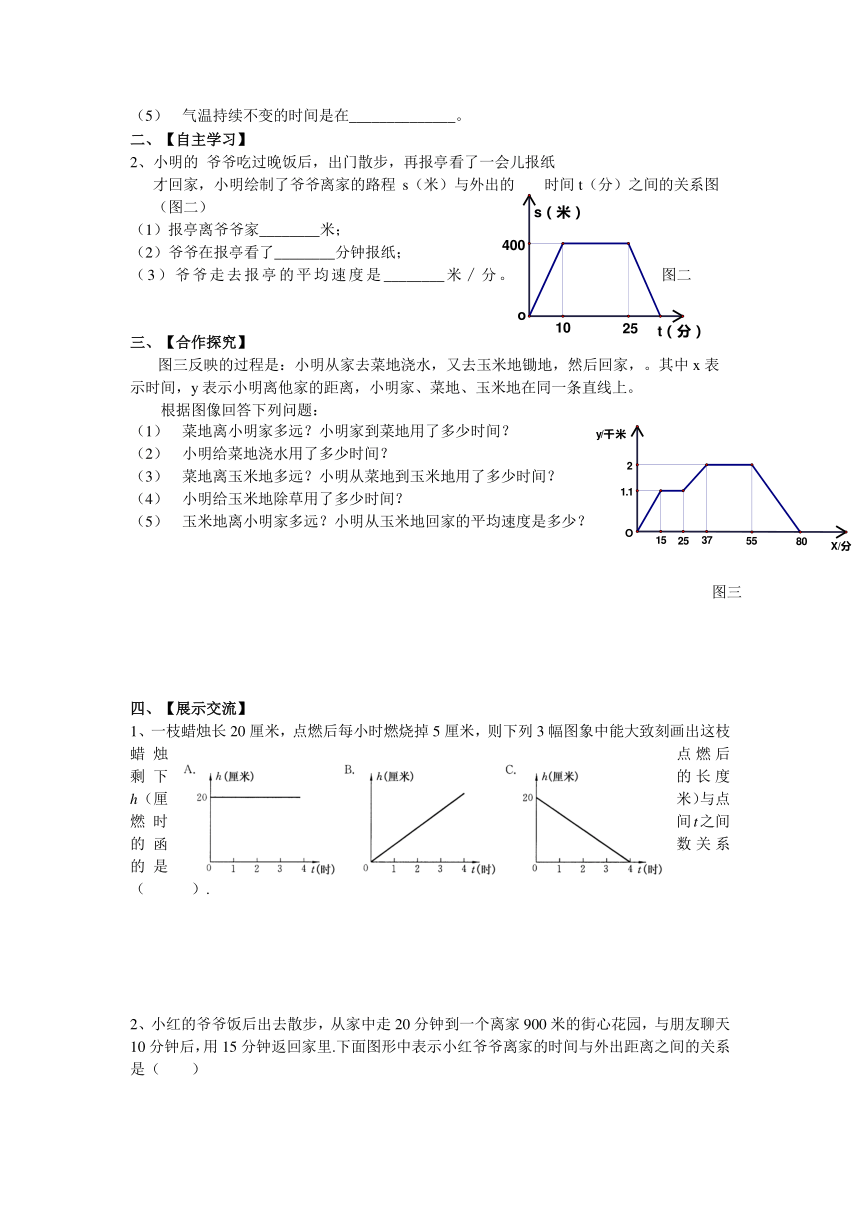
2、小明的 爷爷吃过晚饭后,出门散步,再报亭看了一会儿报纸
才回家,小明绘制了爷爷离家的路程s(米)与外出的时间t(分)之间的关系图
(图二)
(1)报亭离爷爷家________米;
(2)爷爷在报亭看了________分钟报纸;
(3)爷爷走去报亭的平均速度是________米∕分。 图二
三、【合作探究】
图三反映的过程是:小明从家去菜地浇水,又去玉米地锄地,然后回家,。其中x表
示时间,y表示小明离他家的距离,小明家、菜地、玉米地在同一条直线上。
根据图像回答下列问题:
菜地离小明家多远?小明家到菜地用了多少时间?
小明给菜地浇水用了多少时间?
菜地离玉米地多远?小明从菜地到玉米地用了多少时间?
小明给玉米地除草用了多少时间?
玉米地离小明家多远?小明从玉米地回家的平均速度是多少?
四、【展示交流】
1、一枝蜡烛长20厘米,点燃后每小 ( http: / / www.21cnjy.com )时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).
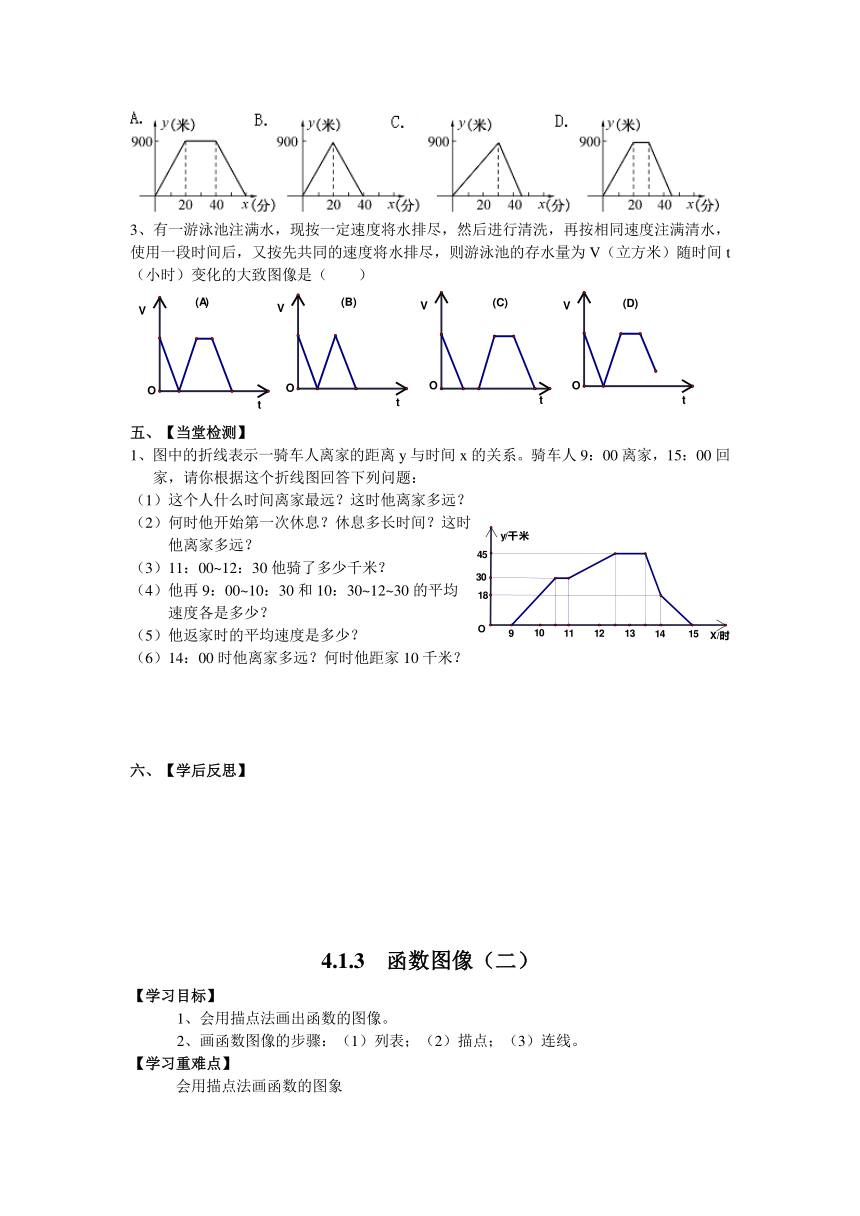
2、小红的爷爷饭后出去散步,从家中走20 ( http: / / www.21cnjy.com )分钟到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家的时间与外出距离之间的关系是( )
3、有一游泳池注满水,现按一定速度将 ( http: / / www.21cnjy.com )水排尽,然后进行清洗,再按相同速度注满清水,使用一段时间后,又按先共同的速度将水排尽,则游泳池的存水量为V(立方米)随时间t(小时)变化的大致图像是( )
五、【当堂检测】
1、图中的折线表示一骑车人离家的距离y与时间x的关系。骑车人9:00离家,15:00回家,请你根据这个折线图回答下列问题:
(1)这个人什么时间离家最远?这时他离家多远?
(2)何时他开始第一次休息?休息多长时间?这时
他离家多远?
(3)11:00~12:30他骑了多少千米?
(4)他再9:00~10:30和10:30~12~30的平均
速度各是多少?
(5)他返家时的平均速度是多少?
(6)14:00时他离家多远?何时他距家10千米?
六、【学后反思】
4.1.3 函数图像(二)
【学习目标】
1、会用描点法画出函数的图像。
2、画函数图像的步骤:(1)列表;(2)描点;(3)连线。
【学习重难点】
会用描点法画函数的图象
【知识链接】
函数的表示方法有哪些?
二、【自主学习】
例1 画出函数y=x2的图象.
分析:要画出一个函数的图象,关键是要画出图象上的一些点,为此,首先要取一些 自变量的值,并求出对应的函数值.(x的取值一定要在它的取值范围内)
解:(1)取x的自变量一些值,例如x=-3,-2,-1,0,1,2,3,。。。。,并且计算出对应的函数值,为方便表达,我们列表如下:
x 。。。 -3 -2 -1 0 1 2 3 。。。
y 。。。 。。。
由此,我们得到一系列的有序实数对:。。。,( ),( ),( ),
( ),( ),( ),( ),。。。
(2)在直角坐标系中描出这些有序实数对的对应点
(3)描完点之后,用光滑的曲线依次把这些点连起来,便可得到这个函数的图象。
这里画函数图象的方法我们称为__________,步骤为:__________________。
三、【合作探究】
1、在所给的直角坐标系中画出函数y=x的图象(先填写下表,再描点、连线).
x -3 -2 -1 0 1 2 3
y
2、画出下列函数的图像
(1) (2)
四、【展示交流】
1、矩形的周长是8cm,设一边长为x cm,另一边长为y cm.
(1)求y关于x的函数关系式,并写出自变量x的取值范围;
(2)在给出的坐标系中,作出函数图像。
五、【当堂检测】
1、王强在电脑上进行高尔夫球的模拟练习,在某处按函数关系式y=击球,球正好进洞.其中,y(m)是球的飞行高度,x(m)是球飞出的水平距离.
试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的起点与洞之间的距离是多少?
解:(1) 列表如下:
从图象上看,高尔夫球的最大飞行高度是______m,球的起点与洞之间的距离是_____m。
六、【学后反思】
4.1.4 函数图像(三)
【学习目标】
1、会根据题目中题意或图表写出函数解析式;
2、根据函数解析式解决问题。
【学习重难点】
根据函数解析式解决问题,学会确定自变量的取值范围
【知识链接】
画出下列函数的图像:
二、【自主学习】
例1:一辆汽车的油箱中现有汽油50L, ( http: / / www.21cnjy.com )如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减小,平均耗油量为0.1 L / km。
写出表示y与x的函数关系式,这样的式子叫做函数解析式。
指出自变量x的取值范围;
汽车行驶200km时,邮箱中还有多少汽油?
练习:拖拉机开始工作时,邮箱中有油30L,每小时耗油5L。
写出邮箱中的余油量Q(L)与工作时间t(h)之间的函数关系式;
求出自变量t的取值范围;
画出函数图象;
根据图像回答拖拉机工作2小时后,邮箱余油是多少?若余油10L,拖拉机工作了几小时?
三、【合作探究】
例2:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
t / 时 0 1 2 3 4 5
y / 米 10 10.5 10.10 10.15 10.20 10.25
由记录表推出这5小时中水位高度y(单位:米)岁时间t(单位:时)变化的函数解析式,并画出函数图像;
据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米?
四、【展示交流】
练习:有一根弹簧最多可挂10kg重的物体,测得该弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如下关系:
x(kg) 0 1 2 3 4 5
y(cm) 12 12.5 13 13.5 14 14.5
写出y与x的函数关系式,并求出自变量的取值范围;
画出函数图像;
根据函数图像回答,当弹簧长为16.5cm时,所挂的物体质量是多少kg?当所挂物体质量为8kg的时候,弹簧的长为多少cm?
五、【当堂检测】
1、某种活期储蓄的月利率是0. ( http: / / www.21cnjy.com )06%,存入100元本金,则本息和y(元)随所存月数x变化的函数解析式为______________,当存期为4个月的时候,本息和为________元;
2、正方向边长为3,若边长增加x则面积 ( http: / / www.21cnjy.com )增加y,则y随x变化的函数解析式为____________,若面积增加了16 ,则变成增加了___________;
3、甲车速度为20米/秒,乙车速度为25米 ( http: / / www.21cnjy.com )/秒,现甲车在乙车前面500米,设x秒后两车之间的距离为y米,则y随x变化的函数解析式为________________,自变量x的取值范围是______________;
4、某学校组织学生到炬力千米的博物馆无参观,小红因事没能乘上学校的包车,于是准备在学校门口改乘出租车去博物馆,车租车的收费标准如下:
里程 收费
3千米及3千米以下 7.00
3千米以上,每增加1千米 2.00
请写出出租车行驶的里程数x(千米)与费用y(元)之间的函数关系式;
小红同学身上仅有14元钱,乘出租车到博物馆的车费够不够,请说明理由。
5、声音在空气中传播速度和气温间有如下关系:
气温(℃) 0 5 10 15 20
声速(m/s) 331 334 337 340 343
若用t表示气温,V表示声速,请写出V随t变化的函数解析式;
当声速为361m/s的时候,气温是多少?
【学后反思】
4.2.1 正比例函数
【学习目标】
1、理解正比例函数的概念
2、会画正比例函数的图像,理解正比例函数的性质。
【学习重难点】
1、理解正比例函数意义及解析式的特点
2、掌握正比例函数图象的性质特点。
一、【知识链接】
按下列要求写出解析式
(1)一本笔记本的单价为2元,现购买x本与付费y元的关系式为_________________;
(2)若正方形的周长为P,边长为a,那么边长a与周长p之间的关系式为______________;
(3)一辆汽车的速度为60 km / h ,则行使路程s与行使时间t之间的关系式为_________;
(4)圆的半径为r,则圆的周长c与半径r之间的关系式为______________。
二、【自主学习】
一般地,形如 (k是常数,k≠0)的函数,叫做 ,其中k叫做比例系数。
练习:1、下列函数钟,那些是正比例函数?______________
(1) (2) (3) (4) (5)
(6) (7) (8)
2、关于x的函数是正比例函数,则m__________
画出下列正比例函数
(1) (2)
x -2 -1 0 1 2
y
x -2 -1 0 1 2
y
比较上面两个图像,填写你发现的规律:
(1)两个图像都是经过原点的 __________,
(2)函数的图像经过第_____象限,从左到右_______,即y随x的增大而_______;
(3)函数的图像经过第_____象限,从左到右______,即y随x的增大而_______;
三、【合作探究】
总结:正比例函数的解析式为__________________
相同点
图像所在象限
图像大致形状
增减性
【展示交流】
1、关于函数,下列结论中,正确的是( )
A、函数图像经过点(1,3) B、函数图像经过二、四象限
C、y随x的增大而增大 D、不论x为何值,总有y>0
2、已知正比例函数的图像过第二、四象限,则( )
A、y随x的增大而增大 B、y随x的增大而减小
C、当时,y随x的增大而增大;当时,y随x的增大而减少;
D、不论x如何变化,y不变。
3、当时,函数的图像在第( )象限。
A、一、三 B、二、四 C、二 D、三
4、函数的图像经过点P(-1,3)则k的值为( )
A、3 B、—3 C、 D、
五、【当堂检测】
5、若A(1,m)在函数的图像上,则m=________,则点A关于y轴对称点坐标是___________;
6、若B(m,6)在函数的图像上,则m=________,则点A关于x轴对称点坐标是___________;
7、y与x成正比例,当x=3时,,则y关于x的函数关系式是____________
8、函数的图像在第_______象限,经过点(0,____)与点(1,____),y随x的增大而_________
9、一个函数的图像是经过原点的直线,并且这条直线经过点(1,-3),求这个函数解析式。
六、【学后反思】
4.2.2 一次函数(二)
【学习目标】
1、懂得画一次函数的图像,清楚知道一次函数之间的关系
2、理解一次函数图像的性质,了解中的k,b对函数图像的影响
【学习重难点】
1.一次函数的图象的画法。
2.一次函数的图象特征与解析式联系。
一、【知识链接】
在同一个直角坐标系中画出函数,,的图像
-2 -1 0 1 2
y=2x
y=2x+3
y=2x-3
二、【自主学习】
观察这三个图像,这三个函数图像形状都是_________,并且倾斜度_______。函数的图像经过原点,函数与y轴交于点________,即它可以看作由直线向_____平移_____个单位长度得到;同样的,函数与y轴交于点________,即它可以看作由直线向_____平移_____个单位长度得到。
猜想:一次函数的图像是一条________,当时,它是由向_____平移_____个单位长度得到;当时,它是由向_____平移_____个单位长度得到。
练习:
在同一个直角坐标系中,把直线向_______平移_____个单位就得到的图像;若向_______平移_____个单位就得到的图像。
(1)将直线向下平移2个单位,可得直线________;
(2)将直线向_____平移______个单位可得直线。
例2 :分别画出下列函数的图像
(1) (2) (3) (4)
分析:由于一次函数的图像是直线,所以只要确定两个点就能画出它,一般选取直线与x轴,y轴的交点。
(1) (2) (3) (4)
x 0
y 0
观察上面四个图像,(1)经过_________象限;y随x的增大而_______,函数的图像从左到右________;(2)经过_________象限;y随x的增大而_______,函数的图像从左到右________;(3)经过_________象限;y随x的增大而_______,函数的图像从左到右________;(4)经过_________象限;y随x的增大而_______,函数的图像从左到右________。
三、【合作探究】
1、由此可以得到直线中,k ,b的取值决定直线的位置:
(1)直线经过___________象限;
(2)直线经过___________象限;
(3)直线经过___________象限;
(4)直线经过___________象限;
2、一次函数的性质:
(1)当时,y随x的增大而_______,这时函数的图像从左到右_______;
(2)当时,y随x的增大而_______,这时函数的图像从左到右_______;
四、【展示交流】
1、一次函数的图像不经过( )
A、第一象限 B、第二象限 C、 第三想象限 D、 第四象限
2、已知直线不经过第三象限,也不经过原点,则下列结论正确的是( )
A、 B、 C、 D、
3、下列函数中,y随x的增大而增大的是( )
A、 B、 C、 D、
4、对于一次函数,函数值y随x的增大而减小,则k的取值范围是( )
A、 B、 C、 D、
5、一次函数的图像一定经过( )
A、(3,5) B、(-2,3) C、(2,7) D、(4、10)
6、已知正比例函数的函数值y随x的增大而增大,则一次函数的图像大致是( )
五、【当堂检测】
7、一次函数的图像如图所示,则k_______,
b_______,y随x的增大而_________
8、一次函数的图像经过___________象限,
y随x的增大而_________ (第6题)
9、已知点(-1,a)、(2,b)在直线 上,则a,b的大小关系是__________
10、直线与x轴交点坐标为__________;与y轴交点坐标_________;图像经过__________象限,y随x的增大而____________,图像与坐标轴所围成的三角形的面积是___________
11、已知一次函数的图像经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数关系式_____________
12、已知一次函数图像(1) ( http: / / www.21cnjy.com )不经过第二象限,(2)经过点(2,-5),请写出一个同时满足(1)和(2)这两个条件的函数关系式:_______________
六、【学后反思】
4.2.3 一次函数(三)
【学习目标】
学会运用待定系数法和数形结合思想求一次函数解析式
【知识链接】:什么是一次函数?
【自主学习】
例1:已知一次函数的图像经过点(3,5)与(2,3),求这个一次函数的解析式。
分析:求一次函数的解析式,关键是求出k,b的值,从已知条件可以列出关于k,b的二元一次方程组,并求出k,b。
解: ∵一次函数经过点(3,5)与(2,3)
∴
解得
∴一次函数的解析式为_______________
像例1这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体
写出这个式子的方法,叫做待定系数法。
1、已知一次函数,当x = 5时,y = 4,
(1)求这个一次函数。 (2)求当时,函数y的值。
2、已知直线经过点(9,0)和点(24,20),求这条直线的函数解析式。
3、已知弹簧的长度 y(厘米)在一定的限度内是所挂重物质量 x(千克)的一次函数.现
已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2
厘米.求这个一次函数的关系式.
三、【合作探究】
例2:已知一次函数的图象如图所示,求出它的函数关系式
练习:已知一次函数的图象如图所示,求出它的函数关系式
四、【展示交流】
为了学生的身体健康,学校课桌、凳的高度 ( http: / / www.21cnjy.com )都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:
( http: / / www.21cnjy.com )
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
五、【当堂检测】
1、A(1,4),B(2,m),C(6,-1)在同一条直线上,求m的值。
2、已知一次函数的图像经过点A(2,2)和点B(-2,-4)
(1)求AB的函数解析式;
(2)求图像与x轴、y轴的交点坐标C、D,并求出直线AB与坐标轴所围成的面积;
(3)如果点M(a,)和N(-4,b)在直线AB上,求a,b的值。
六、【学后反思】
4.3.1 一次函数与一元一次方程
【学习目标】
1、进一步认识和理解一次函数,同时进一步巩固一元一次方程的解法。
2、弄通一次函数与x轴的交点与一元一次方程的解的关系。
【知识链接】:用待定系数法求一次 函数解析式步骤是什么?
【自主学习】
1、解方程2x+4=0
2、自变量x为何值时函数y=2x+4的值为0?
3、以上方程2x+4=0与函数y=2x+4有什么关系?
4、是不是任何一个一元一次方程都可以转化为ax+b=0(a、b是常数,a≠0)?
三、【合作探究】
一个物体现在的速度是3m/秒,其速度每秒增加2m/秒,再过几秒它的速度为11m/秒?
1)、此问题用方程来解如何去解?
2)、画出y=2x-8的函数图象
如果速度y是时间x的函数,则上述问题与y=2x+3有什么关系?如何去解上述问题?
四、【展示交流】
1、解方程ax+b=0(a、b为常数,a≠0)
2、自变量x为何值时,一次函数y=ax+b的值为0,这句话与解方程ax+b=0(a、b为常数)到底有什么关系?
整体感知
如何理解一次函数与x轴交点的横坐标与解方程的关系?
五、【当堂检测】
A、基础知识巩固
1、当自变量x的取值满足什么条件时,函数y=5x+7的值满足下列条件
(1)、y=0 (2)、y=20
B、能力提升
当自变量x取何值时,函数y=+1与y=5x+17的值相等?
六、【学后反思】
4.3.2 一次函数与一元一次不等式
【学习目标】、
1、会用一次函数的图像解一元一次不等式,理解一次函数与一元一次不等式的关系,
2、经历从“数”与“形”两个角度解决问题的过程,体会数形结合的思想。
3、利用一次函数的图像确定一元一次不等式的解集
一、【知识链接】:一次函数与方程有什么关系?
二、【自主学习】
1、什么是一元一次不等式?它的解集是什么?
2、看下面两个问题有什么关系
(1)、解不等式5x+6>3x+10
(2)、自变量x为何值时,函数y=2x-4的值大于0?
3、由上面两个问题的关系,能进一步得到“解不等式ax+b>0与求自变量x在什么范围内一次函数y=ax+b的值大于0”有什么关系?
4、一元一次不等式与一次函数有什么联系?
任何一元一次不等式都可以转化为____ ( http: / / www.21cnjy.com )________或_____________(a、b为常数,a≠0) 的形式,所以解一元一次不等式可以看作是:当一次函数值大(小)于0时,求________相应的______________
三、【合作探究】
用画图像法解不等式,首先要把不等式转化 ( http: / / www.21cnjy.com )为函数的形式,根据图像判断不等式的解集,两种解法都把不等式转化为比较___________________的高低
如图:直线y=kx+b经过点A(-3,-2),B(2,4),根据图像解答下列问题:
(1)、求k,b的值
(2)、指明不等式>0的解集
(3)、求不等式>4的解
(4)、解不等式6x+8<-10
四、【展示交流】
用画函数图像的方法解不等式5x+4<2x+10
解法1:原不等式化为3x-6<0,画出直线y ( http: / / www.21cnjy.com )=3x-6,可以看出,当x<2时_______________________,即y=3x-6<0,所以不等式的解集为x<2.
解法2:将原不等式的两边分别看作两个一次函数,分别为:y=5x+4与直线y=2x+10,在同一坐标系内画出图像
如图所示,它们交点的横坐标为2,当x<2时,对于同一个x,直线y=5x+4上的点在直线y=2x+10的下方,所以不等式的解集为x<2.
1、从函数值的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的
___________________的取值范围。
2、从函数图像的角度看,就是确定直线y=kx+b在x轴上方(或下方)部分所
3、理解y>0,y=0,y<0的几何意义:
一次函数y=kx+b,图像在x轴上方时,y____0,图像在x轴上时,y____0,图像在轴下方时,y____0.
五、【当堂检测】
1、已知一次函数y=kx+b的图像如图,当x<时,y的取值范围是( )
A、y>0 B、y<0 C、-2<y<0 D、y<-2
2、一次函数的图像如图,则它的解析式是_____________________.
当x=______时,y=0 当x_______时,y>0 当y_______时,x<0
3、利用函数图象解出x
(1)、5x-1=2x+5 (2)、6x-4<3x+2
4、利用函数图象解不等式
(1)、5x-1>2x+5 (2)、x-4<3x+1
六、【学后反思】
中国人口数统计表
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
图一
图三
【学习目标】
1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;
2、学会用含一个变量的代数式表示另一个变量;
3、结合实例,理解函数的概念以及自变量的意义;在理解掌握函数概念的基础上,确定函数关系式;
4、会根据函数解析式和实际意义确定自变量的取值范围。
【学习重点】了解常量与变量的意义;理解函数概念和自变量的意义;确定函数关系式。
【学习难点】函数概念的理解;函数关系式的确定
学习过程:
一、【知识链接】
问题一:一辆汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.
1.请同学们根据题意填写下表:
t/时 1 2 3 4 5 t
s/千米
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含t的式子表示s.__s=_________________t的取值范围是
这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
二、【自主学习】
问题二:每张电影票的售价为10元,如果早 ( http: / / www.21cnjy.com )场售出票150张,午场售出205张,晚场售出310张,三场电影的票房收入各多少元?设一场电影售票x张,票房收入y元.怎样用含x的式子表示y
1.请同学们根据题意填写下表:
售出票数(张) 早场150 午场206 晚场310 x
收入y (元)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示y.__y=_________________x的取值范围是
这个问题反映了票房收入_________随售票张数_________的变化过程.
问题三:在一根弹簧的下端悬挂重物,改变并记 ( http: / / www.21cnjy.com )录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律.如果弹簧原长10cm,每1kg重物使弹簧伸长0.5cm,设重物质量为mkg,受力后的弹簧长度为L cm,怎样用含m的式子表示L?
1.请同学们根据题意填写下表:
所挂重物(kg) 1 2 3 4 5 m
受力后的弹簧长度L(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含m的式子表示L.__L=_________________m的取值范围是
这个问题反映了_________随_________的变化过程.
三、【合作探究】
问题四:圆的面积和它的半径之间的关系是什么 ( http: / / www.21cnjy.com )?要画一个面积为10cm2的圆,圆的半径应取多少?圆的面积为20cm2呢?30 cm2呢 怎样用含有圆面积S的式子表示圆半径r? 关系式:________
1.请同学们根据题意填写下表:
面积s(cm2) 10 20 30 s
半径r(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含s的式子表示r.__r=_________________s的取值范围是
这个问题反映了___ _ 随_ __的变化过程.
问题五:用10m长的绳子围 ( http: / / www.21cnjy.com )成矩形,试改变矩形的长度,观察矩形的面积怎样变化.记录不同的矩形的长度值,计算相应的矩形面积的值,探索它们的变化规律。设矩形的长为xm,面积为Sm2,怎样用含有x的式子表示S呢?
1.请同学们根据题意填写下表:
长x(m) 1 2 3 4 x
面积s(m2)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示s. _______________x的取值范围是
这个问题反映了矩形的___ _ 随_ __的变化过程.
四、【展示交流】
小结:以上这些问题都反映了不同事物的变 ( http: / / www.21cnjy.com )化过程,其实现实生活中还有好多类似的问题,在这些变化过程中,有些量的值是按照某种规律变化的(如……),有些量的数值是始终不变的(如……)。
得出结论: 在一个变化过程中,我们称数值发生变化的量为________;
在一个变化过程中,我们称数值始终不变的量为________;
(一)观察探究:
1、在前面研究的每个问题中,都出现了______个变量,它们之间是相互影响,相互制约的.
2、同一个问题中的变量之间有什么联 ( http: / / www.21cnjy.com )系?(请同学们自己分析“问题一”中两个变量之间的关系,进而再分析上述所有实例中的两个变量之间是否有类似的关系.)
归纳:上面每个问题中的两个变量相互联系,当其中一个变量取定一个值时,另一个变量就有________确定的值与其对应。
3、其实,在一些用图或表格表达的问题中,也能看到两个变量间有上述这样的关系.我们来看下面两个问题,通过观察、思考、讨论后回答:
(1)下图是体检时的心电图.其中图 ( http: / / www.21cnjy.com )上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?
( http: / / www.21cnjy.com )
(2)在下面的我国人口数统计表中,年份与人口 ( http: / / www.21cnjy.com )数可以记作两个变量x与y,对于表中每一个确定的年份(x),都对应着一个确定的人口数(y)吗?中国人口数统计表
(二)归纳概念:
一般地,在一个变化过程 ( http: / / www.21cnjy.com )中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是_________,y是x的________.如果当x=a时y=b,那么b叫做当自变量的值为a时的_________.
举例说明:
问题一 问题二 问题三 问题四 问题五
自变量
自变量的函数
函数解析式
五、【当堂检测】
1、若球体体积为V,半径为R,则V=R3.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,R的取值范围是
2、校园里栽下一棵小树高 ( http: / / www.21cnjy.com )1.8米,以后每年长0.3米,则n年后的树高L与年数n之间的函数关系式__________.其中变量是_______、_______,常量是________.自变量是 , 是 的函数,n的取值范围是
3、在男子1500米赛跑中,运动员的平 ( http: / / www.21cnjy.com )均速度v= ,则这个关系式中变量是_______、_______,常量是________.自变量是 , 是 的函数,自变量的取值范围是
4、已知2x-3y=1,若把y看成x的 ( http: / / www.21cnjy.com )函数,则可以表示为___________.其中变量是_____、_____,常量是________.自变量是 , 是 的函数,x的取值范围是
六、【学后反思】
4.1.2函数的图象(一)
【学习目标】
会观察函数图象,从函数图像中获取信息,解决问题。
【学习重难点】
初步掌握画函数图象的方法;通过观察、分析函数图象来获取信息.
一、【知识链接】
1、如图一,是北京春季某一天的气温T随时间t变化的图象,看图回答:
气温最高是_______℃,在_______时,气温最低是_______℃,在______时;
12时的气温是_______℃,20时的气温是_______℃;
气温为-2℃的是在_______时;
气温不断下降的时间是在______________;
气温持续不变的时间是在______________。
二、【自主学习】
2、小明的 爷爷吃过晚饭后,出门散步,再报亭看了一会儿报纸
才回家,小明绘制了爷爷离家的路程s(米)与外出的时间t(分)之间的关系图
(图二)
(1)报亭离爷爷家________米;
(2)爷爷在报亭看了________分钟报纸;
(3)爷爷走去报亭的平均速度是________米∕分。 图二
三、【合作探究】
图三反映的过程是:小明从家去菜地浇水,又去玉米地锄地,然后回家,。其中x表
示时间,y表示小明离他家的距离,小明家、菜地、玉米地在同一条直线上。
根据图像回答下列问题:
菜地离小明家多远?小明家到菜地用了多少时间?
小明给菜地浇水用了多少时间?
菜地离玉米地多远?小明从菜地到玉米地用了多少时间?
小明给玉米地除草用了多少时间?
玉米地离小明家多远?小明从玉米地回家的平均速度是多少?
四、【展示交流】
1、一枝蜡烛长20厘米,点燃后每小 ( http: / / www.21cnjy.com )时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).
2、小红的爷爷饭后出去散步,从家中走20 ( http: / / www.21cnjy.com )分钟到一个离家900米的街心花园,与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家的时间与外出距离之间的关系是( )
3、有一游泳池注满水,现按一定速度将 ( http: / / www.21cnjy.com )水排尽,然后进行清洗,再按相同速度注满清水,使用一段时间后,又按先共同的速度将水排尽,则游泳池的存水量为V(立方米)随时间t(小时)变化的大致图像是( )
五、【当堂检测】
1、图中的折线表示一骑车人离家的距离y与时间x的关系。骑车人9:00离家,15:00回家,请你根据这个折线图回答下列问题:
(1)这个人什么时间离家最远?这时他离家多远?
(2)何时他开始第一次休息?休息多长时间?这时
他离家多远?
(3)11:00~12:30他骑了多少千米?
(4)他再9:00~10:30和10:30~12~30的平均
速度各是多少?
(5)他返家时的平均速度是多少?
(6)14:00时他离家多远?何时他距家10千米?
六、【学后反思】
4.1.3 函数图像(二)
【学习目标】
1、会用描点法画出函数的图像。
2、画函数图像的步骤:(1)列表;(2)描点;(3)连线。
【学习重难点】
会用描点法画函数的图象
【知识链接】
函数的表示方法有哪些?
二、【自主学习】
例1 画出函数y=x2的图象.
分析:要画出一个函数的图象,关键是要画出图象上的一些点,为此,首先要取一些 自变量的值,并求出对应的函数值.(x的取值一定要在它的取值范围内)
解:(1)取x的自变量一些值,例如x=-3,-2,-1,0,1,2,3,。。。。,并且计算出对应的函数值,为方便表达,我们列表如下:
x 。。。 -3 -2 -1 0 1 2 3 。。。
y 。。。 。。。
由此,我们得到一系列的有序实数对:。。。,( ),( ),( ),
( ),( ),( ),( ),。。。
(2)在直角坐标系中描出这些有序实数对的对应点
(3)描完点之后,用光滑的曲线依次把这些点连起来,便可得到这个函数的图象。
这里画函数图象的方法我们称为__________,步骤为:__________________。
三、【合作探究】
1、在所给的直角坐标系中画出函数y=x的图象(先填写下表,再描点、连线).
x -3 -2 -1 0 1 2 3
y
2、画出下列函数的图像
(1) (2)
四、【展示交流】
1、矩形的周长是8cm,设一边长为x cm,另一边长为y cm.
(1)求y关于x的函数关系式,并写出自变量x的取值范围;
(2)在给出的坐标系中,作出函数图像。
五、【当堂检测】
1、王强在电脑上进行高尔夫球的模拟练习,在某处按函数关系式y=击球,球正好进洞.其中,y(m)是球的飞行高度,x(m)是球飞出的水平距离.
试画出高尔夫球飞行的路线;
(2)从图象上看,高尔夫球的最大飞行高度是多少?球的起点与洞之间的距离是多少?
解:(1) 列表如下:
从图象上看,高尔夫球的最大飞行高度是______m,球的起点与洞之间的距离是_____m。
六、【学后反思】
4.1.4 函数图像(三)
【学习目标】
1、会根据题目中题意或图表写出函数解析式;
2、根据函数解析式解决问题。
【学习重难点】
根据函数解析式解决问题,学会确定自变量的取值范围
【知识链接】
画出下列函数的图像:
二、【自主学习】
例1:一辆汽车的油箱中现有汽油50L, ( http: / / www.21cnjy.com )如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减小,平均耗油量为0.1 L / km。
写出表示y与x的函数关系式,这样的式子叫做函数解析式。
指出自变量x的取值范围;
汽车行驶200km时,邮箱中还有多少汽油?
练习:拖拉机开始工作时,邮箱中有油30L,每小时耗油5L。
写出邮箱中的余油量Q(L)与工作时间t(h)之间的函数关系式;
求出自变量t的取值范围;
画出函数图象;
根据图像回答拖拉机工作2小时后,邮箱余油是多少?若余油10L,拖拉机工作了几小时?
三、【合作探究】
例2:一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
t / 时 0 1 2 3 4 5
y / 米 10 10.5 10.10 10.15 10.20 10.25
由记录表推出这5小时中水位高度y(单位:米)岁时间t(单位:时)变化的函数解析式,并画出函数图像;
据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米?
四、【展示交流】
练习:有一根弹簧最多可挂10kg重的物体,测得该弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如下关系:
x(kg) 0 1 2 3 4 5
y(cm) 12 12.5 13 13.5 14 14.5
写出y与x的函数关系式,并求出自变量的取值范围;
画出函数图像;
根据函数图像回答,当弹簧长为16.5cm时,所挂的物体质量是多少kg?当所挂物体质量为8kg的时候,弹簧的长为多少cm?
五、【当堂检测】
1、某种活期储蓄的月利率是0. ( http: / / www.21cnjy.com )06%,存入100元本金,则本息和y(元)随所存月数x变化的函数解析式为______________,当存期为4个月的时候,本息和为________元;
2、正方向边长为3,若边长增加x则面积 ( http: / / www.21cnjy.com )增加y,则y随x变化的函数解析式为____________,若面积增加了16 ,则变成增加了___________;
3、甲车速度为20米/秒,乙车速度为25米 ( http: / / www.21cnjy.com )/秒,现甲车在乙车前面500米,设x秒后两车之间的距离为y米,则y随x变化的函数解析式为________________,自变量x的取值范围是______________;
4、某学校组织学生到炬力千米的博物馆无参观,小红因事没能乘上学校的包车,于是准备在学校门口改乘出租车去博物馆,车租车的收费标准如下:
里程 收费
3千米及3千米以下 7.00
3千米以上,每增加1千米 2.00
请写出出租车行驶的里程数x(千米)与费用y(元)之间的函数关系式;
小红同学身上仅有14元钱,乘出租车到博物馆的车费够不够,请说明理由。
5、声音在空气中传播速度和气温间有如下关系:
气温(℃) 0 5 10 15 20
声速(m/s) 331 334 337 340 343
若用t表示气温,V表示声速,请写出V随t变化的函数解析式;
当声速为361m/s的时候,气温是多少?
【学后反思】
4.2.1 正比例函数
【学习目标】
1、理解正比例函数的概念
2、会画正比例函数的图像,理解正比例函数的性质。
【学习重难点】
1、理解正比例函数意义及解析式的特点
2、掌握正比例函数图象的性质特点。
一、【知识链接】
按下列要求写出解析式
(1)一本笔记本的单价为2元,现购买x本与付费y元的关系式为_________________;
(2)若正方形的周长为P,边长为a,那么边长a与周长p之间的关系式为______________;
(3)一辆汽车的速度为60 km / h ,则行使路程s与行使时间t之间的关系式为_________;
(4)圆的半径为r,则圆的周长c与半径r之间的关系式为______________。
二、【自主学习】
一般地,形如 (k是常数,k≠0)的函数,叫做 ,其中k叫做比例系数。
练习:1、下列函数钟,那些是正比例函数?______________
(1) (2) (3) (4) (5)
(6) (7) (8)
2、关于x的函数是正比例函数,则m__________
画出下列正比例函数
(1) (2)
x -2 -1 0 1 2
y
x -2 -1 0 1 2
y
比较上面两个图像,填写你发现的规律:
(1)两个图像都是经过原点的 __________,
(2)函数的图像经过第_____象限,从左到右_______,即y随x的增大而_______;
(3)函数的图像经过第_____象限,从左到右______,即y随x的增大而_______;
三、【合作探究】
总结:正比例函数的解析式为__________________
相同点
图像所在象限
图像大致形状
增减性
【展示交流】
1、关于函数,下列结论中,正确的是( )
A、函数图像经过点(1,3) B、函数图像经过二、四象限
C、y随x的增大而增大 D、不论x为何值,总有y>0
2、已知正比例函数的图像过第二、四象限,则( )
A、y随x的增大而增大 B、y随x的增大而减小
C、当时,y随x的增大而增大;当时,y随x的增大而减少;
D、不论x如何变化,y不变。
3、当时,函数的图像在第( )象限。
A、一、三 B、二、四 C、二 D、三
4、函数的图像经过点P(-1,3)则k的值为( )
A、3 B、—3 C、 D、
五、【当堂检测】
5、若A(1,m)在函数的图像上,则m=________,则点A关于y轴对称点坐标是___________;
6、若B(m,6)在函数的图像上,则m=________,则点A关于x轴对称点坐标是___________;
7、y与x成正比例,当x=3时,,则y关于x的函数关系式是____________
8、函数的图像在第_______象限,经过点(0,____)与点(1,____),y随x的增大而_________
9、一个函数的图像是经过原点的直线,并且这条直线经过点(1,-3),求这个函数解析式。
六、【学后反思】
4.2.2 一次函数(二)
【学习目标】
1、懂得画一次函数的图像,清楚知道一次函数之间的关系
2、理解一次函数图像的性质,了解中的k,b对函数图像的影响
【学习重难点】
1.一次函数的图象的画法。
2.一次函数的图象特征与解析式联系。
一、【知识链接】
在同一个直角坐标系中画出函数,,的图像
-2 -1 0 1 2
y=2x
y=2x+3
y=2x-3
二、【自主学习】
观察这三个图像,这三个函数图像形状都是_________,并且倾斜度_______。函数的图像经过原点,函数与y轴交于点________,即它可以看作由直线向_____平移_____个单位长度得到;同样的,函数与y轴交于点________,即它可以看作由直线向_____平移_____个单位长度得到。
猜想:一次函数的图像是一条________,当时,它是由向_____平移_____个单位长度得到;当时,它是由向_____平移_____个单位长度得到。
练习:
在同一个直角坐标系中,把直线向_______平移_____个单位就得到的图像;若向_______平移_____个单位就得到的图像。
(1)将直线向下平移2个单位,可得直线________;
(2)将直线向_____平移______个单位可得直线。
例2 :分别画出下列函数的图像
(1) (2) (3) (4)
分析:由于一次函数的图像是直线,所以只要确定两个点就能画出它,一般选取直线与x轴,y轴的交点。
(1) (2) (3) (4)
x 0
y 0
观察上面四个图像,(1)经过_________象限;y随x的增大而_______,函数的图像从左到右________;(2)经过_________象限;y随x的增大而_______,函数的图像从左到右________;(3)经过_________象限;y随x的增大而_______,函数的图像从左到右________;(4)经过_________象限;y随x的增大而_______,函数的图像从左到右________。
三、【合作探究】
1、由此可以得到直线中,k ,b的取值决定直线的位置:
(1)直线经过___________象限;
(2)直线经过___________象限;
(3)直线经过___________象限;
(4)直线经过___________象限;
2、一次函数的性质:
(1)当时,y随x的增大而_______,这时函数的图像从左到右_______;
(2)当时,y随x的增大而_______,这时函数的图像从左到右_______;
四、【展示交流】
1、一次函数的图像不经过( )
A、第一象限 B、第二象限 C、 第三想象限 D、 第四象限
2、已知直线不经过第三象限,也不经过原点,则下列结论正确的是( )
A、 B、 C、 D、
3、下列函数中,y随x的增大而增大的是( )
A、 B、 C、 D、
4、对于一次函数,函数值y随x的增大而减小,则k的取值范围是( )
A、 B、 C、 D、
5、一次函数的图像一定经过( )
A、(3,5) B、(-2,3) C、(2,7) D、(4、10)
6、已知正比例函数的函数值y随x的增大而增大,则一次函数的图像大致是( )
五、【当堂检测】
7、一次函数的图像如图所示,则k_______,
b_______,y随x的增大而_________
8、一次函数的图像经过___________象限,
y随x的增大而_________ (第6题)
9、已知点(-1,a)、(2,b)在直线 上,则a,b的大小关系是__________
10、直线与x轴交点坐标为__________;与y轴交点坐标_________;图像经过__________象限,y随x的增大而____________,图像与坐标轴所围成的三角形的面积是___________
11、已知一次函数的图像经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数关系式_____________
12、已知一次函数图像(1) ( http: / / www.21cnjy.com )不经过第二象限,(2)经过点(2,-5),请写出一个同时满足(1)和(2)这两个条件的函数关系式:_______________
六、【学后反思】
4.2.3 一次函数(三)
【学习目标】
学会运用待定系数法和数形结合思想求一次函数解析式
【知识链接】:什么是一次函数?
【自主学习】
例1:已知一次函数的图像经过点(3,5)与(2,3),求这个一次函数的解析式。
分析:求一次函数的解析式,关键是求出k,b的值,从已知条件可以列出关于k,b的二元一次方程组,并求出k,b。
解: ∵一次函数经过点(3,5)与(2,3)
∴
解得
∴一次函数的解析式为_______________
像例1这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体
写出这个式子的方法,叫做待定系数法。
1、已知一次函数,当x = 5时,y = 4,
(1)求这个一次函数。 (2)求当时,函数y的值。
2、已知直线经过点(9,0)和点(24,20),求这条直线的函数解析式。
3、已知弹簧的长度 y(厘米)在一定的限度内是所挂重物质量 x(千克)的一次函数.现
已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2
厘米.求这个一次函数的关系式.
三、【合作探究】
例2:已知一次函数的图象如图所示,求出它的函数关系式
练习:已知一次函数的图象如图所示,求出它的函数关系式
四、【展示交流】
为了学生的身体健康,学校课桌、凳的高度 ( http: / / www.21cnjy.com )都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:
( http: / / www.21cnjy.com )
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
五、【当堂检测】
1、A(1,4),B(2,m),C(6,-1)在同一条直线上,求m的值。
2、已知一次函数的图像经过点A(2,2)和点B(-2,-4)
(1)求AB的函数解析式;
(2)求图像与x轴、y轴的交点坐标C、D,并求出直线AB与坐标轴所围成的面积;
(3)如果点M(a,)和N(-4,b)在直线AB上,求a,b的值。
六、【学后反思】
4.3.1 一次函数与一元一次方程
【学习目标】
1、进一步认识和理解一次函数,同时进一步巩固一元一次方程的解法。
2、弄通一次函数与x轴的交点与一元一次方程的解的关系。
【知识链接】:用待定系数法求一次 函数解析式步骤是什么?
【自主学习】
1、解方程2x+4=0
2、自变量x为何值时函数y=2x+4的值为0?
3、以上方程2x+4=0与函数y=2x+4有什么关系?
4、是不是任何一个一元一次方程都可以转化为ax+b=0(a、b是常数,a≠0)?
三、【合作探究】
一个物体现在的速度是3m/秒,其速度每秒增加2m/秒,再过几秒它的速度为11m/秒?
1)、此问题用方程来解如何去解?
2)、画出y=2x-8的函数图象
如果速度y是时间x的函数,则上述问题与y=2x+3有什么关系?如何去解上述问题?
四、【展示交流】
1、解方程ax+b=0(a、b为常数,a≠0)
2、自变量x为何值时,一次函数y=ax+b的值为0,这句话与解方程ax+b=0(a、b为常数)到底有什么关系?
整体感知
如何理解一次函数与x轴交点的横坐标与解方程的关系?
五、【当堂检测】
A、基础知识巩固
1、当自变量x的取值满足什么条件时,函数y=5x+7的值满足下列条件
(1)、y=0 (2)、y=20
B、能力提升
当自变量x取何值时,函数y=+1与y=5x+17的值相等?
六、【学后反思】
4.3.2 一次函数与一元一次不等式
【学习目标】、
1、会用一次函数的图像解一元一次不等式,理解一次函数与一元一次不等式的关系,
2、经历从“数”与“形”两个角度解决问题的过程,体会数形结合的思想。
3、利用一次函数的图像确定一元一次不等式的解集
一、【知识链接】:一次函数与方程有什么关系?
二、【自主学习】
1、什么是一元一次不等式?它的解集是什么?
2、看下面两个问题有什么关系
(1)、解不等式5x+6>3x+10
(2)、自变量x为何值时,函数y=2x-4的值大于0?
3、由上面两个问题的关系,能进一步得到“解不等式ax+b>0与求自变量x在什么范围内一次函数y=ax+b的值大于0”有什么关系?
4、一元一次不等式与一次函数有什么联系?
任何一元一次不等式都可以转化为____ ( http: / / www.21cnjy.com )________或_____________(a、b为常数,a≠0) 的形式,所以解一元一次不等式可以看作是:当一次函数值大(小)于0时,求________相应的______________
三、【合作探究】
用画图像法解不等式,首先要把不等式转化 ( http: / / www.21cnjy.com )为函数的形式,根据图像判断不等式的解集,两种解法都把不等式转化为比较___________________的高低
如图:直线y=kx+b经过点A(-3,-2),B(2,4),根据图像解答下列问题:
(1)、求k,b的值
(2)、指明不等式>0的解集
(3)、求不等式>4的解
(4)、解不等式6x+8<-10
四、【展示交流】
用画函数图像的方法解不等式5x+4<2x+10
解法1:原不等式化为3x-6<0,画出直线y ( http: / / www.21cnjy.com )=3x-6,可以看出,当x<2时_______________________,即y=3x-6<0,所以不等式的解集为x<2.
解法2:将原不等式的两边分别看作两个一次函数,分别为:y=5x+4与直线y=2x+10,在同一坐标系内画出图像
如图所示,它们交点的横坐标为2,当x<2时,对于同一个x,直线y=5x+4上的点在直线y=2x+10的下方,所以不等式的解集为x<2.
1、从函数值的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的
___________________的取值范围。
2、从函数图像的角度看,就是确定直线y=kx+b在x轴上方(或下方)部分所
3、理解y>0,y=0,y<0的几何意义:
一次函数y=kx+b,图像在x轴上方时,y____0,图像在x轴上时,y____0,图像在轴下方时,y____0.
五、【当堂检测】
1、已知一次函数y=kx+b的图像如图,当x<时,y的取值范围是( )
A、y>0 B、y<0 C、-2<y<0 D、y<-2
2、一次函数的图像如图,则它的解析式是_____________________.
当x=______时,y=0 当x_______时,y>0 当y_______时,x<0
3、利用函数图象解出x
(1)、5x-1=2x+5 (2)、6x-4<3x+2
4、利用函数图象解不等式
(1)、5x-1>2x+5 (2)、x-4<3x+1
六、【学后反思】
中国人口数统计表
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
图一
图三
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
