初中数学人教版八年级下册17.1《勾股定理》课件 20张PPT
文档属性
| 名称 | 初中数学人教版八年级下册17.1《勾股定理》课件 20张PPT |
|
|
| 格式 | ppt | ||
| 文件大小 | 939.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 00:00:00 | ||
图片预览

文档简介
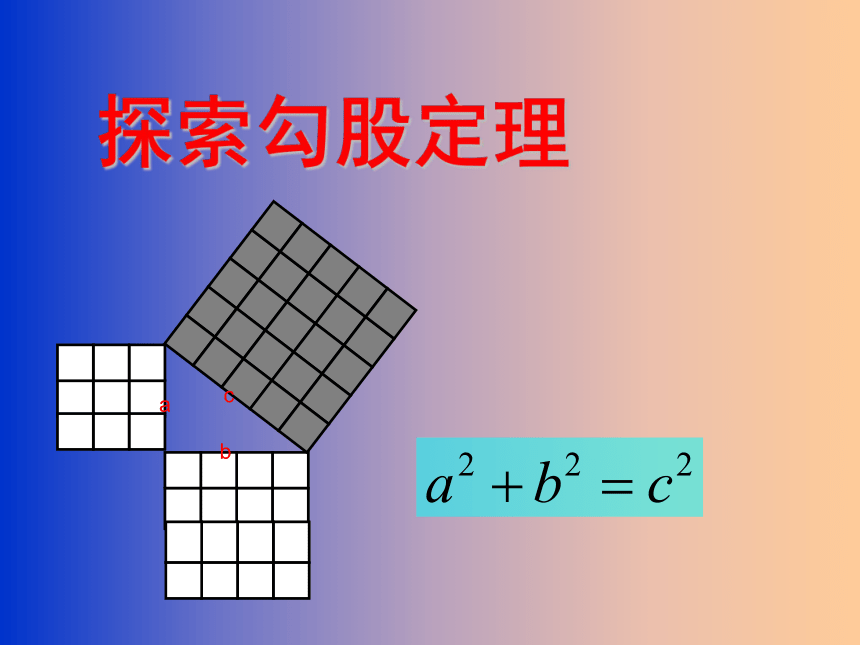
(共20张PPT)
探索勾股定理
a
b
c
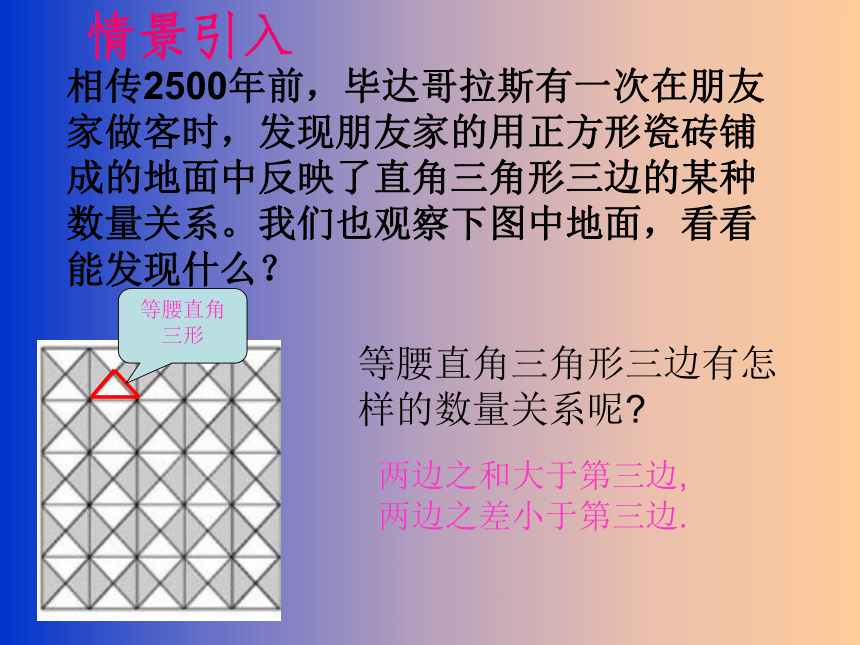
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用正方形瓷砖铺成的地面中反映了直角三角形三边的某种数量关系。我们也观察下图中地面,看看能发现什么?
情景引入
等腰直角三形
等腰直角三角形三边有怎样的数量关系呢
两边之和大于第三边,两边之差小于第三边.
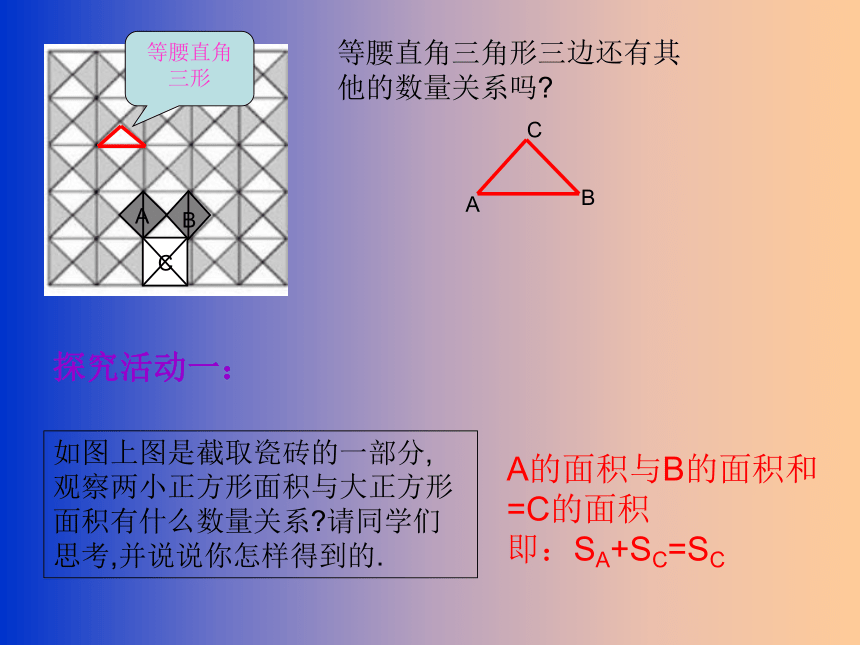
等腰直角三形
等腰直角三角形三边还有其他的数量关系吗
如图上图是截取瓷砖的一部分, 观察两小正方形面积与大正方形面积有什么数量关系 请同学们思考,并说说你怎样得到的.
探究活动一:
A
C
B
A
B
C
A的面积与B的面积和=C的面积
即:SA+SC=SC
C
B
A
C
B
A
C
B
A
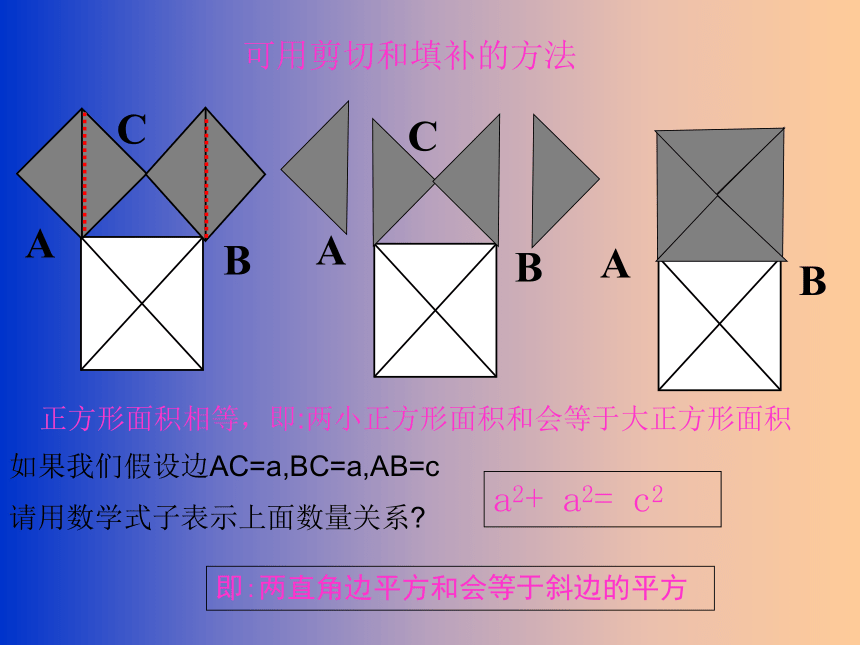
可用剪切和填补的方法
正方形面积相等,即:两小正方形面积和会等于大正方形面积
如果我们假设边AC=a,BC=a,AB=c
请用数学式子表示上面数量关系
a2+ a2= c2
即:两直角边平方和会等于斜边的平方
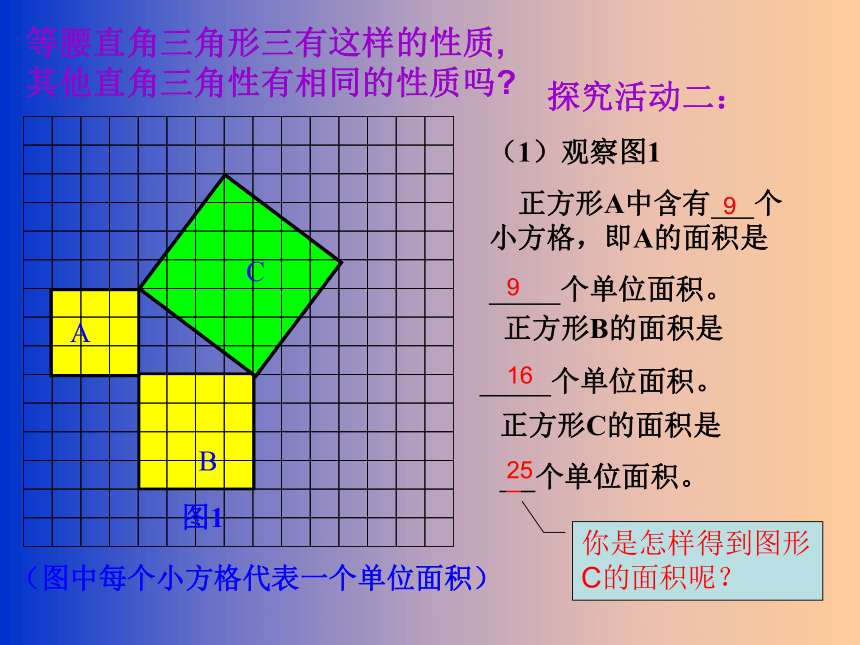
等腰直角三角形三有这样的性质,其他直角三角性有相同的性质吗
(图中每个小方格代表一个单位面积)
图1
A
B
C
(1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
探究活动二:
9
9
16
25
你是怎样得到图形C的面积呢?
(图中每个小方格代表一个单位面积)
图1
(图中每个小方格代表一个单位面积)
图1
A
B
C
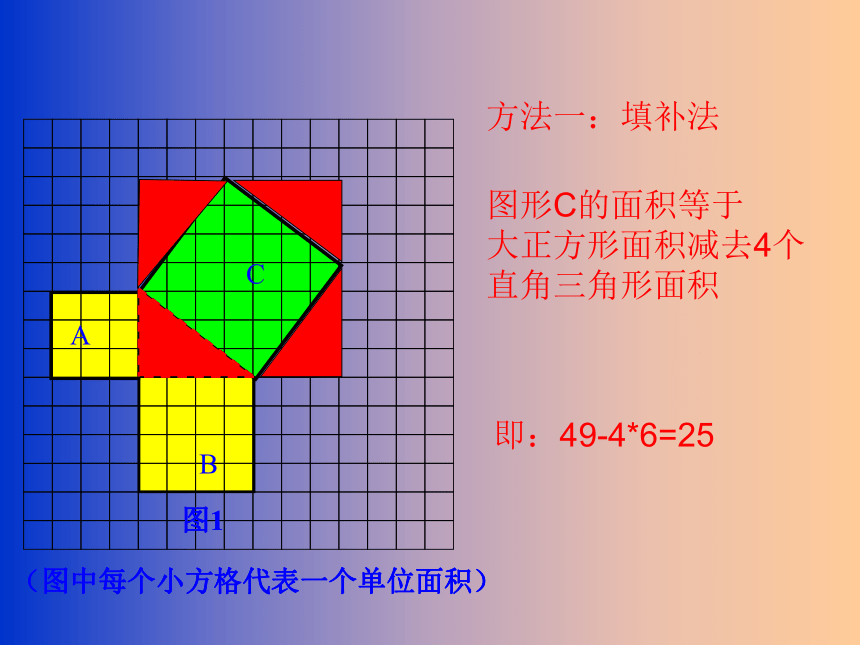
方法一:填补法
图形C的面积等于
大正方形面积减去4个直角三角形面积
即:49-4*6=25
(图中每个小方格代表一个单位面积)
图1
(图中每个小方格代表一个单位面积)
图1
A
B
C
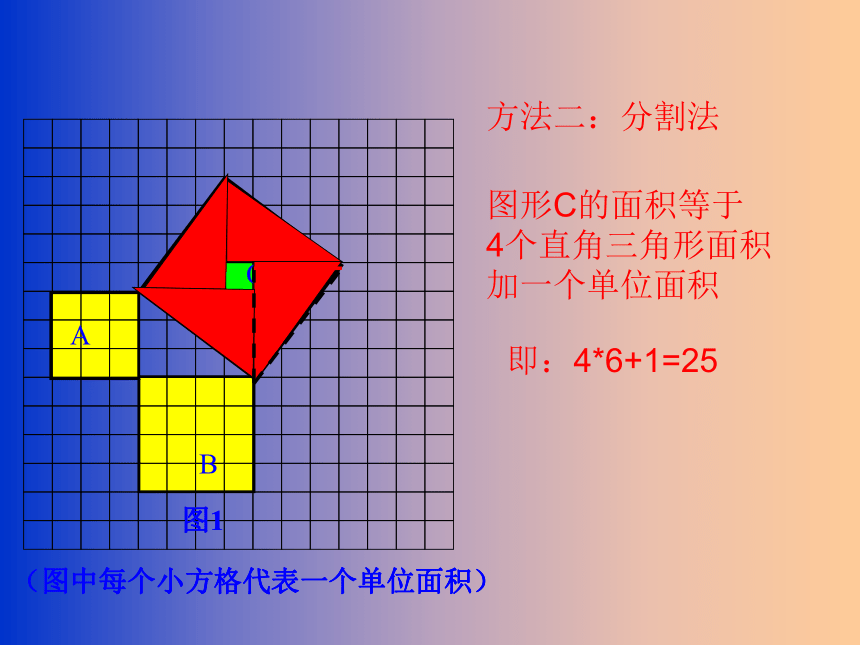
方法二:分割法
图形C的面积等于
4个直角三角形面积加一个单位面积
即:4*6+1=25
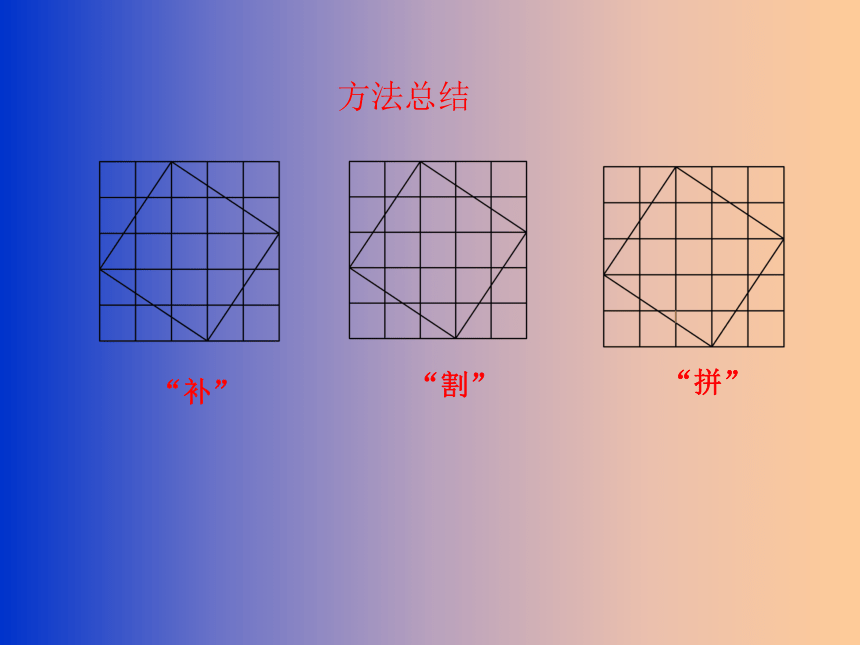
“割”
“补”
“拼”
方法总结
(图中每个小方格代表一个单位面积)
图1
A
B
C
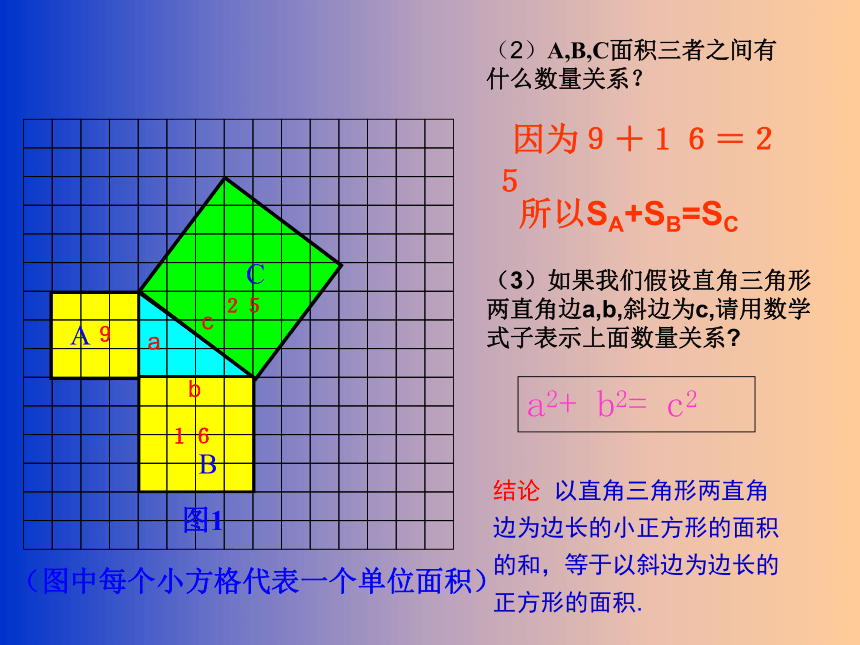
(2)A,B,C面积三者之间有什么数量关系?
a
c
b
(3)如果我们假设直角三角形两直角边a,b,斜边为c,请用数学式子表示上面数量关系
a2+ b2= c2
结论 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
因为9+16=25
9
25
16
所以SA+SB=SC
勾股定理
在直角三角形中,如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
表示为:Rt△ABC中,∠C=90°
则
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
a
b
c
c2=a2 + b2
c=?
a=?
b=?
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
这个定理在中国又称为“商高定理”,商高是公元
前十一世纪的中国人。当时中国的朝代是西周,
是奴隶社会时期。在中国古代大约是战国时期西汉
的数学著作《周髀算经》中记录着商高同周公的
一段对话。商高说:“…故折矩,勾广三,股修四,
经隅五。商高那段话的意思就是说:当直角三角形
的两条直角边分别为3(短边)和4(长边)时,
径隅(就是弦)则为5。以后人们就简单地把这个
事实说成“勾三股四弦五”。由于勾股定理的内容
最早见于商高的话中,所以人们就把这个定理叫
作"商高定理"。
勾股定理的由来
勾股定理的由来
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为"毕达哥拉斯定理",以后就流传开了。
勾股定理有很许多证明方法,像我国汉代“赵爽弦图“,和西方毕达哥拉斯,下图是毕达哥拉斯的证法:图中S1=S2,你能写出证明过程吗
活动三:勾股定理的证明:a2+ b2= c2
而
所以
即
因为
图1
图2
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
活动四
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
6
30°
2
17
8
45°
2
D
A
B
C
3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
活动五:小结
1、用”补”和”割”推倒勾股定理
2、勾股定理
3、勾股定理证明
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
4、勾股定理简单应用.
课本习题:1、2
探索勾股定理
a
b
c
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用正方形瓷砖铺成的地面中反映了直角三角形三边的某种数量关系。我们也观察下图中地面,看看能发现什么?
情景引入
等腰直角三形
等腰直角三角形三边有怎样的数量关系呢
两边之和大于第三边,两边之差小于第三边.
等腰直角三形
等腰直角三角形三边还有其他的数量关系吗
如图上图是截取瓷砖的一部分, 观察两小正方形面积与大正方形面积有什么数量关系 请同学们思考,并说说你怎样得到的.
探究活动一:
A
C
B
A
B
C
A的面积与B的面积和=C的面积
即:SA+SC=SC
C
B
A
C
B
A
C
B
A
可用剪切和填补的方法
正方形面积相等,即:两小正方形面积和会等于大正方形面积
如果我们假设边AC=a,BC=a,AB=c
请用数学式子表示上面数量关系
a2+ a2= c2
即:两直角边平方和会等于斜边的平方
等腰直角三角形三有这样的性质,其他直角三角性有相同的性质吗
(图中每个小方格代表一个单位面积)
图1
A
B
C
(1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
探究活动二:
9
9
16
25
你是怎样得到图形C的面积呢?
(图中每个小方格代表一个单位面积)
图1
(图中每个小方格代表一个单位面积)
图1
A
B
C
方法一:填补法
图形C的面积等于
大正方形面积减去4个直角三角形面积
即:49-4*6=25
(图中每个小方格代表一个单位面积)
图1
(图中每个小方格代表一个单位面积)
图1
A
B
C
方法二:分割法
图形C的面积等于
4个直角三角形面积加一个单位面积
即:4*6+1=25
“割”
“补”
“拼”
方法总结
(图中每个小方格代表一个单位面积)
图1
A
B
C
(2)A,B,C面积三者之间有什么数量关系?
a
c
b
(3)如果我们假设直角三角形两直角边a,b,斜边为c,请用数学式子表示上面数量关系
a2+ b2= c2
结论 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
因为9+16=25
9
25
16
所以SA+SB=SC
勾股定理
在直角三角形中,如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
表示为:Rt△ABC中,∠C=90°
则
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
a
b
c
c2=a2 + b2
c=?
a=?
b=?
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
这个定理在中国又称为“商高定理”,商高是公元
前十一世纪的中国人。当时中国的朝代是西周,
是奴隶社会时期。在中国古代大约是战国时期西汉
的数学著作《周髀算经》中记录着商高同周公的
一段对话。商高说:“…故折矩,勾广三,股修四,
经隅五。商高那段话的意思就是说:当直角三角形
的两条直角边分别为3(短边)和4(长边)时,
径隅(就是弦)则为5。以后人们就简单地把这个
事实说成“勾三股四弦五”。由于勾股定理的内容
最早见于商高的话中,所以人们就把这个定理叫
作"商高定理"。
勾股定理的由来
勾股定理的由来
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为"毕达哥拉斯定理",以后就流传开了。
勾股定理有很许多证明方法,像我国汉代“赵爽弦图“,和西方毕达哥拉斯,下图是毕达哥拉斯的证法:图中S1=S2,你能写出证明过程吗
活动三:勾股定理的证明:a2+ b2= c2
而
所以
即
因为
图1
图2
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
活动四
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
6
30°
2
17
8
45°
2
D
A
B
C
3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
活动五:小结
1、用”补”和”割”推倒勾股定理
2、勾股定理
3、勾股定理证明
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
4、勾股定理简单应用.
课本习题:1、2
