16.3 可化为一元一次方程的分式方程-分式方程的定义试题
文档属性
| 名称 | 16.3 可化为一元一次方程的分式方程-分式方程的定义试题 |  | |
| 格式 | zip | ||
| 文件大小 | 62.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-08 19:36:48 | ||
图片预览


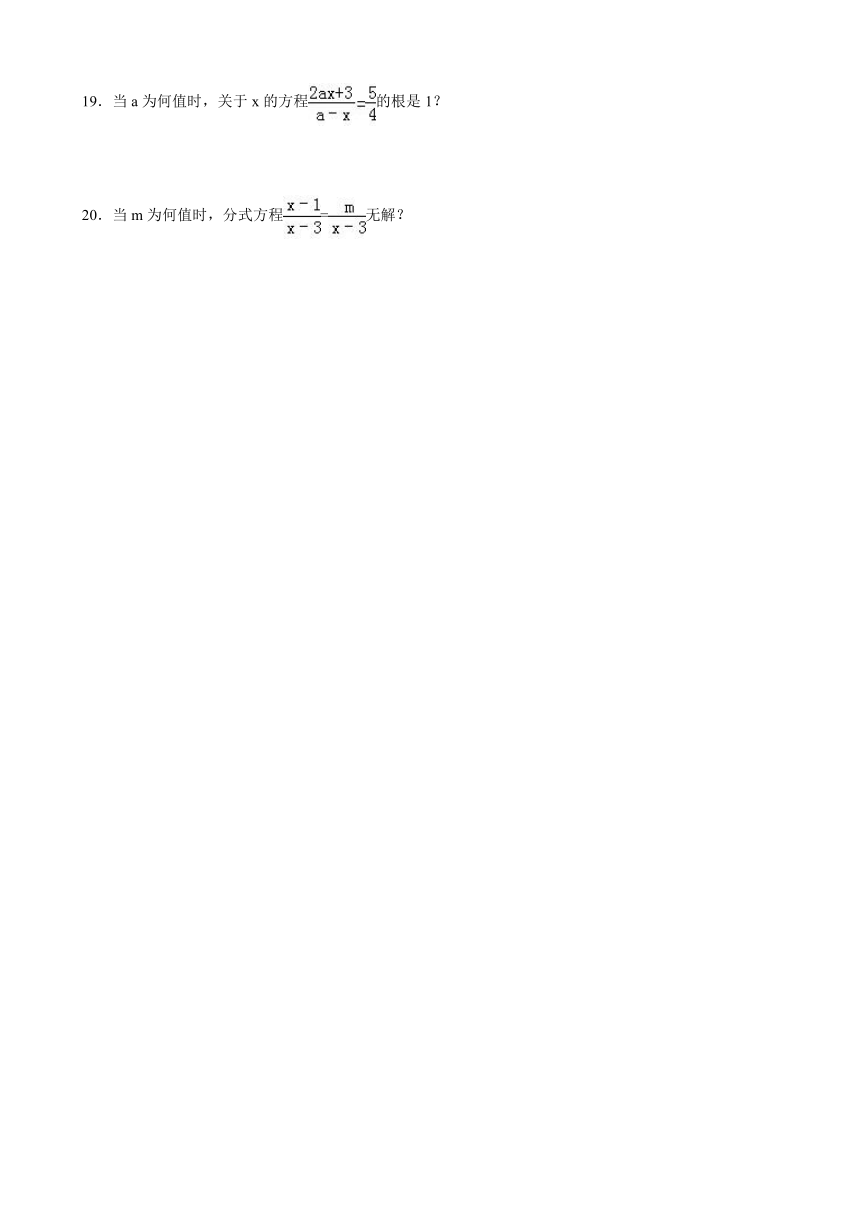


文档简介
16.3.1分式方程的定义
一.选择题(共8小题)
1.在下列方程中,关于x的分式方程的个数有( )
①;②;③;④.
A.2个 B.3个 C.4个 D.1个
2.在下列各式中,是关于x的分式方程的是( )
A.2x﹣3y=0 B.﹣3= C.= D.+3
3.下列说法:
①解分式方程一定会产生增根;
②方程=0的根为2;
③方程的最简公分母为2x(2x﹣4);
④x+=1+是分式方程.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.方程的解为( )
A.x= B.x= C.x=﹣2 D.无解
5.若x=﹣1是方程﹣=0的根,则( )
A.a=6 B.a=﹣6 C.a=3 D.a=﹣3
6.若关于x的分式方程=1的解为正数,则m的取值范围是( )
A.m>3 B.m≠﹣2 C.m>﹣3且m≠1 D.m>﹣3且m≠﹣2
7.下列各式中,不是分式方程的是( )
A. B. C. D.
8.下列方程是分式方程的是( )
A. B. C. D.
二.填空题(共6小题)
9.在下列方程:①、②、③、④、⑤中,分式方程的个数有 _________ .
10.分母中含有 _________ 的方程,叫做分式方程.
11.若关于x的方程的解为正数,则m的取值范围是 _________ .
12.已知关于x的方程的解是负数,则m的取值范围为 _________ .
13.分式方程的解为 _________ .
14.关于x的分式方程无解,则m的值是 _________ .
三.解答题(共6小题)
15.若关于x的方程+1=无解,则m= _________ .
16.若关于x的分式方程的解是正数,求a的取值范围.
17.已知x=5是方程=的解,求a的值.
18.关于x的方程﹣=﹣1无解,求m的值.
19.当a为何值时,关于x的方程的根是1?
20.当m为何值时,分式方程=无解?
16.3.1分式方程的定义
参考答案与试题解析
一.选择题(共8小题)
1.在下列方程中,关于x的分式方程的个数有( )
①;②;③;④.
A. 2个 B.3个 C.4个 D. 1个
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义:分母里含有字母的方程叫做分式方程进行判断.
解答: 解:①方程分母中不含未知数,故①不是分式方程;
②方程分母中含未知数,故②是分式方程;
③方程分母中含表示未知数的字母,故③是分式方程;
④方程分母中含未知数x,故④是分式方程;
故选:B.
点评: 本题考查了分式方程,判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
2.在下列各式中,是关于x的分式方程的是( )
A. 2x﹣3y=0 B.﹣3= C.= D. +3
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义对各选项进行逐一分析即可.
解答: 解:A、2x﹣3y=0是整式方程,故本选项错误;
B、﹣3=是整式方程,故本选项错误;
C、=是分式方程,故本选项正确;
D、+3不是方程,故本选项错误.
故选C.
点评: 本题考查的是分式方程的定义,熟知分母中含有未知数的方程叫做分式方程是解答此题的关键.
3.下列说法:
①解分式方程一定会产生增根;
②方程=0的根为2;
③方程的最简公分母为2x(2x﹣4);
④x+=1+是分式方程.
其中正确的个数是( )
A. 1个 B.2个 C.3个 D. 4个
考点: 分式方程的定义;分式方程的解;解分式方程;分式方程的增根.21世纪教育网
分析: 根据分式方程的定义、增根的概念及最简公分母的定义解答.
解答: 解:①解分式方程不一定会产生增根;
②方程=0的根为2,分母为0,所以是增根;
③方程的最简公分母为2x(x﹣2);
所以①②③错误,根据分式方程的定义判断④正确.
故选:A.
点评: 判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
4.方程的解为( )
A. x= B.x= C.x=﹣2 D. 无解
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 可以解方程:先去分母得到3(x+1)=x+2,解得x=﹣,然后经验确定分式方程的解;也可以把x=、﹣、﹣2分别代入方程,计算方程左右两边,根据分式方程的解进行判断.
解答: 解:去分母得,3(x+1)=x+2,
解得x=﹣,
经经验x=﹣是原方程的根,
所以原方程的解为x=﹣.
故选B.
点评: 本题考查了分式方程的解:使分式方程左右两边成立的未知数的值叫分式方程的解.也考查了解分式方程.
5.若x=﹣1是方程﹣=0的根,则( )
A. a=6 B.a=﹣6 C.a=3 D. a=﹣3
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 分式方程去分母转化为整式方程,将x=﹣1代入计算即可求出a的值.
解答: 解:去分母得:ax﹣3x+3=0,
将x=﹣1代入得:﹣a+3+3=0,
解得:a=6,
故选A
点评: 此题考查了分式方程的解,本题需注意在任何时候都要考虑分母不为0.
6.若关于x的分式方程=1的解为正数,则m的取值范围是( )
A. m>3 B.m≠﹣2 C.m>﹣3且m≠1 D. m>﹣3且m≠﹣2
考点: 分式方程的解.21世纪教育网
分析: 先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围.
解答: 解:去分母得,m+2=x﹣1,
解得,x=m+3,
∵方程的解是正数,
∴m+3>0,
解这个不等式得,m>﹣3,
∵m+3﹣1≠0,
∴m≠﹣2,
则m的取值范围是m>﹣3且m≠﹣2.
故选D.
点评: 考查了分式方程的解,解题关键是要掌握方程的解的定义,使方程成立的未知数的值叫做方程的解.注意分式方程分母不等于0.
7.下列各式中,不是分式方程的是( )
A. B. C. D.
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义:分母里含有字母的方程叫做分式方程判断.
解答: 解:A、B、C方程中分母中都含有字母,都是分式方程,
D、方程分母中不含未知数,故不是分式方程.
故选D.
点评: 判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
8.下列方程是分式方程的是( )
A. B. C. D.
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义:分母里含有字母的方程叫做分式方程判断.
解答: 解:A、方程分母中含未知数x,故是分式方程;
B、方程分母中不含未知数,故不是分式方程;
C、方程分母中不含未知数,故不是分式方程;
D、方程分母中不含未知数,故不是分式方程.
故选A.
点评: 判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
二.填空题(共6小题)
9.在下列方程:①、②、③、④、⑤中,分式方程的个数有 3 .
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的概念,直接得出结果即可.
解答: 解:分式方程有:③④⑤,
故答案为3.
点评: 本题考查了分式方程的概念,分母中含有未知数的方程叫分式方程.
10.分母中含有 未知数 的方程,叫做分式方程.
考点: 分式方程的定义.21世纪教育网
分析: 分式方程的定义:分母中含有未知数的方程叫做分式方程.
解答: 解:分母中含有字母的方程叫做分式方程.
故答案是:未知数.
点评: 本题考查了分式方程的定义.判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
11.若关于x的方程的解为正数,则m的取值范围是 m>﹣1且m≠1 .
考点: 分式方程的解.21世纪教育网
分析: 先解关于x的分式方程,它的解x用含有m的代数式表示,然后再依据“原方程有解”和“解是正数”建立不等式求m的取值范围.
解答: 解:原方程整理得:m﹣1=2x﹣2,
解得:x=,
∵原方程有解,
∴x﹣1≠0,
即,
解得m≠1,
∵方程的解是正数,
∴>0,
解得m>﹣1,
∴m>﹣1且m≠1,
故应填:m>﹣1且m≠1.
点评: 本题主要考查分式程的解,根据“原方程有解”和“解是正数”这两点建立不等式求m的取值范围.
12.已知关于x的方程的解是负数,则m的取值范围为 m>﹣8且m≠﹣4 .
考点: 分式方程的解.21世纪教育网
分析: 求出分式方程的解x=﹣,得出﹣<0,求出m的范围,根据分式方程得出﹣≠﹣2,求出m,即可得出答案.
解答: 解:,
2x﹣m=4x+8,
﹣2x=8+m,
x=﹣,
∵关于x的方程的解是负数,
∴﹣<0,
解得:m>﹣8,
∵方程,
∴x+2≠0,
即﹣≠﹣2,
∴m≠﹣4,
故答案为:m>﹣8且m≠﹣4.
点评: 本题考查了分式方程的解和解一元一次不等式,关键是得出﹣<0和﹣≠﹣2,题目具有一定的代表性,但是有一定的难度.
13.分式方程的解为 x= .
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 去分母后即可化为整式方程,即可求得x的值,再检验一下即可.
解答: 解:去分母得:1=2(x﹣1),
解得x=,
经检验得;x=是原方程的解.
点评: 解分式方程的基本思想是转化为整式方程,解分式方程时一定要注意检验.
14.关于x的分式方程无解,则m的值是 1 .
考点: 分式方程的解.21世纪教育网
分析: 分式方程去分母转化为整式方程,根据分式方程无解得到x﹣1=0,求出x=1,代入整式方程即可求出m的值.
解答: 解:分式方程去分母得:x﹣2(x﹣1)=m,
由分式方程无解得到x﹣1=0,即x=1,
代入整式方程得:m=1.
故答案为:1.
点评: 此题考查了分式方程的解,注意在任何时候都要考虑分母不为0.
三.解答题(共6小题)
15.若关于x的方程+1=无解,则m= ﹣4 .
考点: 分式方程的解.21世纪教育网
分析: 方程无解,说明方程有增根x=2,只要把增根代入方程然后解出m的值即可.
解答: 解:∵+1=,
∴5+m+x﹣2=1,
∵关于x的方程无解,
∴x=2,
∴5+m+2﹣2=1,
∴m=﹣4.
故答案为:﹣4.
点评: 此题主要考查方程的增根问题,计算时要小心,是一道基础题.
16.若关于x的分式方程的解是正数,求a的取值范围.
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求a的取值范围.
解答: 解:去分母,得2x+a=2﹣x
解得:x=,∴>0
∴2﹣a>0,
∴a<2,且x≠2,
∴a≠﹣4
∴a<2且a≠﹣4.
点评: 由于我们的目的是求a的取值范围,因此也没有必要求得x的值,求得3x=2﹣a即可列出关于a的不等式了,另外,解答本题时,易漏掉a≠﹣4,这是因为忽略了x﹣2≠0这个隐含的条件而造成的,这应引起同学们的足够重视.
17.已知x=5是方程=的解,求a的值.
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 分式方程去分母转化为整式方程,把x=5代入整式方程求出a的值即可.
解答: 解:分式方程去分母得:3=2(x﹣a)(2x+a),
把x=5代入得:3=2(5﹣a)(10+a)=2(50+5a﹣10a﹣a2)=100﹣10a﹣2a2,
整理得:2a2+10a﹣97=0,即a2+5a=,
配方得:a2+5a+=+,即(a+)2=,
开方得:a+=±,
解得:a=.
点评: 此题考查了分式方程的解,注意在任何时候都要考虑分母不为0.
18.关于x的方程﹣=﹣1无解,求m的值.
考点: 分式方程的解.21世纪教育网
分析: 先化简方程,再把x的值代入即可求出m的值.
解答: 解:∵化简x的方程﹣=﹣1,得2m﹣3=﹣(2x+2)
∵x的方程﹣=﹣1无解,
∴方程的解为x=﹣1,
∴2m﹣3=﹣(﹣2+2),解得m=.
点评: 本题主要考查了分式方程的解,解题的关键是化简方程,再把x的值代入.
19.当a为何值时,关于x的方程的根是1?
考点: 分式方程的解.21世纪教育网
分析: 先把分式方程转化为整式方程,然后把x=1代入方程求解即可.
解答: 解:方程两边都乘以4(a﹣x)得,
4(2ax+3)=5(a﹣x),
∵方程的根是1,
∴4(2a+3)=5(a﹣1),
解得a=﹣.
点评: 本题考查了分式方程的解,熟练掌握方程的解的定义把方程的解代入方程,然后准确计算是解题的关键.
20.当m为何值时,分式方程=无解?
考点: 分式方程的解.21世纪教育网
分析: 首先去分母,进而利用分式方程=无解,得出x=3进而得出即可.
解答: 解:去分母得:
x﹣1=m,
x=1+m,
∵分式方程=无解,
∴x﹣3=0,
∴x=3,
1+m=3,
解得;m=2.
点评: 此题主要考查了分式方程的解,根据分式方程无解得出x=3是解题关键.
一.选择题(共8小题)
1.在下列方程中,关于x的分式方程的个数有( )
①;②;③;④.
A.2个 B.3个 C.4个 D.1个
2.在下列各式中,是关于x的分式方程的是( )
A.2x﹣3y=0 B.﹣3= C.= D.+3
3.下列说法:
①解分式方程一定会产生增根;
②方程=0的根为2;
③方程的最简公分母为2x(2x﹣4);
④x+=1+是分式方程.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.方程的解为( )
A.x= B.x= C.x=﹣2 D.无解
5.若x=﹣1是方程﹣=0的根,则( )
A.a=6 B.a=﹣6 C.a=3 D.a=﹣3
6.若关于x的分式方程=1的解为正数,则m的取值范围是( )
A.m>3 B.m≠﹣2 C.m>﹣3且m≠1 D.m>﹣3且m≠﹣2
7.下列各式中,不是分式方程的是( )
A. B. C. D.
8.下列方程是分式方程的是( )
A. B. C. D.
二.填空题(共6小题)
9.在下列方程:①、②、③、④、⑤中,分式方程的个数有 _________ .
10.分母中含有 _________ 的方程,叫做分式方程.
11.若关于x的方程的解为正数,则m的取值范围是 _________ .
12.已知关于x的方程的解是负数,则m的取值范围为 _________ .
13.分式方程的解为 _________ .
14.关于x的分式方程无解,则m的值是 _________ .
三.解答题(共6小题)
15.若关于x的方程+1=无解,则m= _________ .
16.若关于x的分式方程的解是正数,求a的取值范围.
17.已知x=5是方程=的解,求a的值.
18.关于x的方程﹣=﹣1无解,求m的值.
19.当a为何值时,关于x的方程的根是1?
20.当m为何值时,分式方程=无解?
16.3.1分式方程的定义
参考答案与试题解析
一.选择题(共8小题)
1.在下列方程中,关于x的分式方程的个数有( )
①;②;③;④.
A. 2个 B.3个 C.4个 D. 1个
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义:分母里含有字母的方程叫做分式方程进行判断.
解答: 解:①方程分母中不含未知数,故①不是分式方程;
②方程分母中含未知数,故②是分式方程;
③方程分母中含表示未知数的字母,故③是分式方程;
④方程分母中含未知数x,故④是分式方程;
故选:B.
点评: 本题考查了分式方程,判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
2.在下列各式中,是关于x的分式方程的是( )
A. 2x﹣3y=0 B.﹣3= C.= D. +3
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义对各选项进行逐一分析即可.
解答: 解:A、2x﹣3y=0是整式方程,故本选项错误;
B、﹣3=是整式方程,故本选项错误;
C、=是分式方程,故本选项正确;
D、+3不是方程,故本选项错误.
故选C.
点评: 本题考查的是分式方程的定义,熟知分母中含有未知数的方程叫做分式方程是解答此题的关键.
3.下列说法:
①解分式方程一定会产生增根;
②方程=0的根为2;
③方程的最简公分母为2x(2x﹣4);
④x+=1+是分式方程.
其中正确的个数是( )
A. 1个 B.2个 C.3个 D. 4个
考点: 分式方程的定义;分式方程的解;解分式方程;分式方程的增根.21世纪教育网
分析: 根据分式方程的定义、增根的概念及最简公分母的定义解答.
解答: 解:①解分式方程不一定会产生增根;
②方程=0的根为2,分母为0,所以是增根;
③方程的最简公分母为2x(x﹣2);
所以①②③错误,根据分式方程的定义判断④正确.
故选:A.
点评: 判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
4.方程的解为( )
A. x= B.x= C.x=﹣2 D. 无解
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 可以解方程:先去分母得到3(x+1)=x+2,解得x=﹣,然后经验确定分式方程的解;也可以把x=、﹣、﹣2分别代入方程,计算方程左右两边,根据分式方程的解进行判断.
解答: 解:去分母得,3(x+1)=x+2,
解得x=﹣,
经经验x=﹣是原方程的根,
所以原方程的解为x=﹣.
故选B.
点评: 本题考查了分式方程的解:使分式方程左右两边成立的未知数的值叫分式方程的解.也考查了解分式方程.
5.若x=﹣1是方程﹣=0的根,则( )
A. a=6 B.a=﹣6 C.a=3 D. a=﹣3
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 分式方程去分母转化为整式方程,将x=﹣1代入计算即可求出a的值.
解答: 解:去分母得:ax﹣3x+3=0,
将x=﹣1代入得:﹣a+3+3=0,
解得:a=6,
故选A
点评: 此题考查了分式方程的解,本题需注意在任何时候都要考虑分母不为0.
6.若关于x的分式方程=1的解为正数,则m的取值范围是( )
A. m>3 B.m≠﹣2 C.m>﹣3且m≠1 D. m>﹣3且m≠﹣2
考点: 分式方程的解.21世纪教育网
分析: 先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围.
解答: 解:去分母得,m+2=x﹣1,
解得,x=m+3,
∵方程的解是正数,
∴m+3>0,
解这个不等式得,m>﹣3,
∵m+3﹣1≠0,
∴m≠﹣2,
则m的取值范围是m>﹣3且m≠﹣2.
故选D.
点评: 考查了分式方程的解,解题关键是要掌握方程的解的定义,使方程成立的未知数的值叫做方程的解.注意分式方程分母不等于0.
7.下列各式中,不是分式方程的是( )
A. B. C. D.
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义:分母里含有字母的方程叫做分式方程判断.
解答: 解:A、B、C方程中分母中都含有字母,都是分式方程,
D、方程分母中不含未知数,故不是分式方程.
故选D.
点评: 判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
8.下列方程是分式方程的是( )
A. B. C. D.
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的定义:分母里含有字母的方程叫做分式方程判断.
解答: 解:A、方程分母中含未知数x,故是分式方程;
B、方程分母中不含未知数,故不是分式方程;
C、方程分母中不含未知数,故不是分式方程;
D、方程分母中不含未知数,故不是分式方程.
故选A.
点评: 判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
二.填空题(共6小题)
9.在下列方程:①、②、③、④、⑤中,分式方程的个数有 3 .
考点: 分式方程的定义.21世纪教育网
分析: 根据分式方程的概念,直接得出结果即可.
解答: 解:分式方程有:③④⑤,
故答案为3.
点评: 本题考查了分式方程的概念,分母中含有未知数的方程叫分式方程.
10.分母中含有 未知数 的方程,叫做分式方程.
考点: 分式方程的定义.21世纪教育网
分析: 分式方程的定义:分母中含有未知数的方程叫做分式方程.
解答: 解:分母中含有字母的方程叫做分式方程.
故答案是:未知数.
点评: 本题考查了分式方程的定义.判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).
11.若关于x的方程的解为正数,则m的取值范围是 m>﹣1且m≠1 .
考点: 分式方程的解.21世纪教育网
分析: 先解关于x的分式方程,它的解x用含有m的代数式表示,然后再依据“原方程有解”和“解是正数”建立不等式求m的取值范围.
解答: 解:原方程整理得:m﹣1=2x﹣2,
解得:x=,
∵原方程有解,
∴x﹣1≠0,
即,
解得m≠1,
∵方程的解是正数,
∴>0,
解得m>﹣1,
∴m>﹣1且m≠1,
故应填:m>﹣1且m≠1.
点评: 本题主要考查分式程的解,根据“原方程有解”和“解是正数”这两点建立不等式求m的取值范围.
12.已知关于x的方程的解是负数,则m的取值范围为 m>﹣8且m≠﹣4 .
考点: 分式方程的解.21世纪教育网
分析: 求出分式方程的解x=﹣,得出﹣<0,求出m的范围,根据分式方程得出﹣≠﹣2,求出m,即可得出答案.
解答: 解:,
2x﹣m=4x+8,
﹣2x=8+m,
x=﹣,
∵关于x的方程的解是负数,
∴﹣<0,
解得:m>﹣8,
∵方程,
∴x+2≠0,
即﹣≠﹣2,
∴m≠﹣4,
故答案为:m>﹣8且m≠﹣4.
点评: 本题考查了分式方程的解和解一元一次不等式,关键是得出﹣<0和﹣≠﹣2,题目具有一定的代表性,但是有一定的难度.
13.分式方程的解为 x= .
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 去分母后即可化为整式方程,即可求得x的值,再检验一下即可.
解答: 解:去分母得:1=2(x﹣1),
解得x=,
经检验得;x=是原方程的解.
点评: 解分式方程的基本思想是转化为整式方程,解分式方程时一定要注意检验.
14.关于x的分式方程无解,则m的值是 1 .
考点: 分式方程的解.21世纪教育网
分析: 分式方程去分母转化为整式方程,根据分式方程无解得到x﹣1=0,求出x=1,代入整式方程即可求出m的值.
解答: 解:分式方程去分母得:x﹣2(x﹣1)=m,
由分式方程无解得到x﹣1=0,即x=1,
代入整式方程得:m=1.
故答案为:1.
点评: 此题考查了分式方程的解,注意在任何时候都要考虑分母不为0.
三.解答题(共6小题)
15.若关于x的方程+1=无解,则m= ﹣4 .
考点: 分式方程的解.21世纪教育网
分析: 方程无解,说明方程有增根x=2,只要把增根代入方程然后解出m的值即可.
解答: 解:∵+1=,
∴5+m+x﹣2=1,
∵关于x的方程无解,
∴x=2,
∴5+m+2﹣2=1,
∴m=﹣4.
故答案为:﹣4.
点评: 此题主要考查方程的增根问题,计算时要小心,是一道基础题.
16.若关于x的分式方程的解是正数,求a的取值范围.
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求a的取值范围.
解答: 解:去分母,得2x+a=2﹣x
解得:x=,∴>0
∴2﹣a>0,
∴a<2,且x≠2,
∴a≠﹣4
∴a<2且a≠﹣4.
点评: 由于我们的目的是求a的取值范围,因此也没有必要求得x的值,求得3x=2﹣a即可列出关于a的不等式了,另外,解答本题时,易漏掉a≠﹣4,这是因为忽略了x﹣2≠0这个隐含的条件而造成的,这应引起同学们的足够重视.
17.已知x=5是方程=的解,求a的值.
考点: 分式方程的解.21世纪教育网
专题: 计算题.
分析: 分式方程去分母转化为整式方程,把x=5代入整式方程求出a的值即可.
解答: 解:分式方程去分母得:3=2(x﹣a)(2x+a),
把x=5代入得:3=2(5﹣a)(10+a)=2(50+5a﹣10a﹣a2)=100﹣10a﹣2a2,
整理得:2a2+10a﹣97=0,即a2+5a=,
配方得:a2+5a+=+,即(a+)2=,
开方得:a+=±,
解得:a=.
点评: 此题考查了分式方程的解,注意在任何时候都要考虑分母不为0.
18.关于x的方程﹣=﹣1无解,求m的值.
考点: 分式方程的解.21世纪教育网
分析: 先化简方程,再把x的值代入即可求出m的值.
解答: 解:∵化简x的方程﹣=﹣1,得2m﹣3=﹣(2x+2)
∵x的方程﹣=﹣1无解,
∴方程的解为x=﹣1,
∴2m﹣3=﹣(﹣2+2),解得m=.
点评: 本题主要考查了分式方程的解,解题的关键是化简方程,再把x的值代入.
19.当a为何值时,关于x的方程的根是1?
考点: 分式方程的解.21世纪教育网
分析: 先把分式方程转化为整式方程,然后把x=1代入方程求解即可.
解答: 解:方程两边都乘以4(a﹣x)得,
4(2ax+3)=5(a﹣x),
∵方程的根是1,
∴4(2a+3)=5(a﹣1),
解得a=﹣.
点评: 本题考查了分式方程的解,熟练掌握方程的解的定义把方程的解代入方程,然后准确计算是解题的关键.
20.当m为何值时,分式方程=无解?
考点: 分式方程的解.21世纪教育网
分析: 首先去分母,进而利用分式方程=无解,得出x=3进而得出即可.
解答: 解:去分母得:
x﹣1=m,
x=1+m,
∵分式方程=无解,
∴x﹣3=0,
∴x=3,
1+m=3,
解得;m=2.
点评: 此题主要考查了分式方程的解,根据分式方程无解得出x=3是解题关键.
