平面直角坐标系
图片预览




文档简介
17.2.1平面直角坐标系
一.选择题(共9小题)
1.在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图的坐标平面上有P、Q两点,其坐标分别为(5,a)、(b,7).根据图中P、Q两点的位置,判断点(6﹣b,a﹣10)落在第几象限?( )
A.一 B.二 C.三 D.四
3.若点M(x,y)满足(x+y)2=x2+y2﹣2,则点M所在象限是( )
A.第一象限或第三象限 B.第二象限或第四象限 C.第一象限或第二象限 D.不能确定
4.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有( )
A.2个 B.3个 C.4个 D.5个
5. 点P(2,﹣5)关于x轴对称的点的坐标为( )
A.(﹣2,5) B.(2,5) C.(﹣2,﹣5) D.(2,﹣5)
6.在平面直角坐标系中,与点(1,2)关于y轴对称的点的坐标是( )
A.(﹣1,2) B.(1,﹣2) C.(﹣1,﹣2) D.(﹣2,﹣1)
7.如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6),B(﹣6,2),E(2,1),则点D的坐标为( )
A.(﹣4,6) B.(4,6) C.(﹣2,1) D.(6,2)
8.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )
A.(3,2) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
9.点A(1,﹣2)关于x轴对称的点的坐标是( )
A.(1,﹣2) B.(﹣1,2) C.(﹣1,﹣2) D.(1,2)
二.填空题(共7小题)
10.在平面直角坐标系中,点(﹣4,4)在第 _________ 象限.
11.点P(﹣2,3)关于x轴的对称点P′的坐标为 _________ .
12.点P(2,3)关于x轴的对称点的坐标为 _________ .
13.若点M(3,a)关于y轴的对称点是点N(b,2),则(a+b)2014= _________ .
14.已知P(1,﹣2),则点P关于x轴的对称点的坐标是 _________ .
15.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n= _________ .
16.在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数,若累计到正方形AnBnCnDn时,整点共有1680个,则n= _________ .
三.解答题(共5小题)
17.在平面直角坐标系xOy中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.
(1)点A关于原点O的对称点A′的坐标为 _________ ,点B关于x轴的对称点B′的坐标为 _________ ,点C关于y轴的对称点C的坐标为 _________ .
(2)求(1)中的△A′B′C′的面积.
18.请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(0,2),B点坐标为(﹣2,0);
(2)在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.
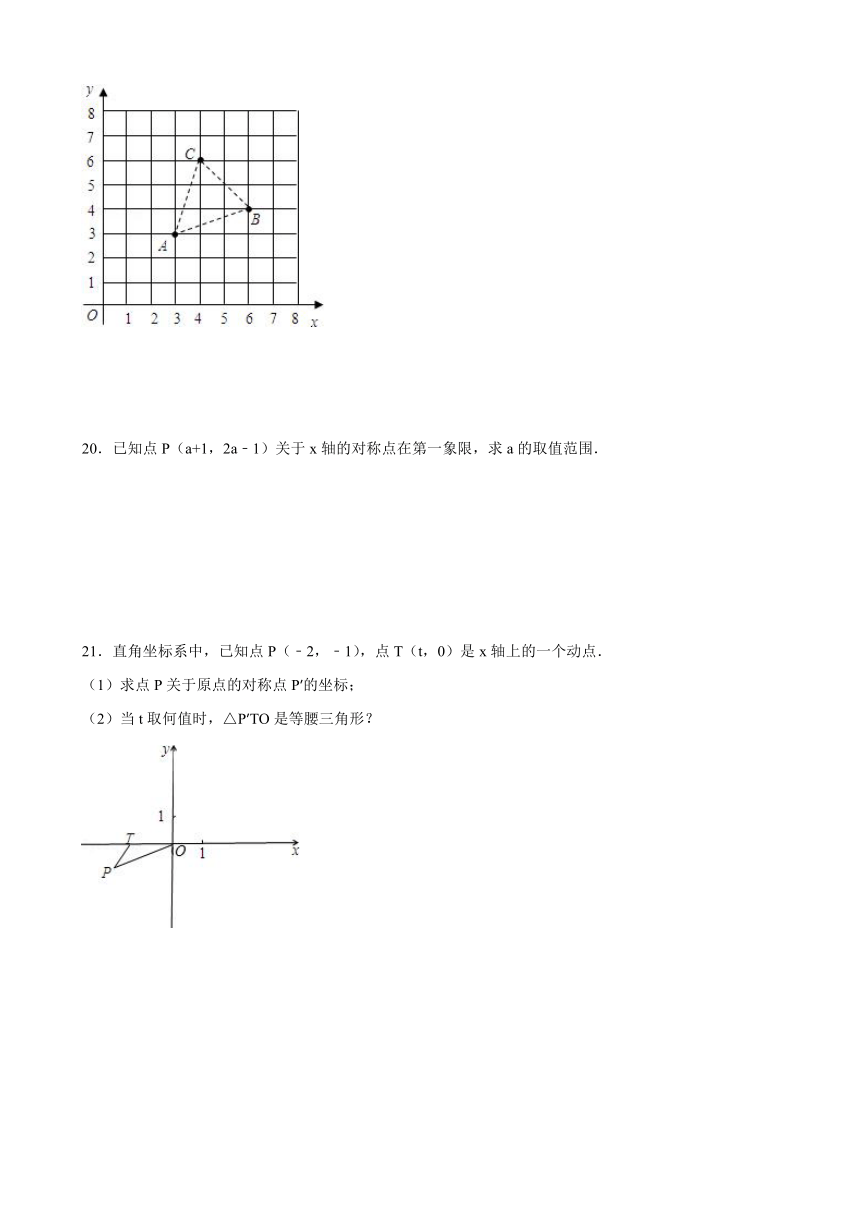
19.如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
20.已知点P(a+1,2a﹣1)关于x轴的对称点在第一象限,求a的取值范围.
21.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
17.2.1平面直角坐标系
参考答案与试题解析
一.选择题(共9小题)
1.在平面直角坐标系中,点M(﹣2,1)在( )
A. 第一象限 B.第二象限 C.第三象限 D. 第四象限
考点: 点的坐标.21世纪教育网
分析: 根据各象限内点的坐标特征解答.
解答: 解:点M(﹣2,1)在第二象限.
故选:B.
点评: 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.如图的坐标平面上有P、Q两点,其坐标分别为(5,a)、(b,7).根据图中P、Q两点的位置,判断点(6﹣b,a﹣10)落在第几象限?( )
A. 一 B.二 C.三 D. 四
考点: 点的坐标.21世纪教育网
分析: 由平面直角坐标系判断出a<7,b<5,然后求出6﹣b,a﹣10的正负情况,再根据各象限内点的坐标特征解答.
解答: 解:∵(5,a)、(b,7),
∴a<7,b<5,
∴6﹣b>0,a﹣10<0,
∴点(6﹣b,a﹣10)在第四象限.
故选D.
点评: 本题考查了点的坐标,观察图形,判断出a、b的取值范围是解题的关键.
3.若点M(x,y)满足(x+y)2=x2+y2﹣2,则点M所在象限是( )
A. 第一象限或第三象限 B. 第二象限或第四象限
C. 第一象限或第二象限 D. 不能确定
考点: 点的坐标;完全平方公式.21世纪教育网
分析: 利用完全平方公式展开得到xy=﹣1,再根据异号得负判断出x、y异号,然后根据各象限内点的坐标特征解答.
解答: 解:∵(x+y)2=x2+2xy+y2,
∴原式可化为xy=﹣1,
∴x、y异号,
∴点M(x,y)在第二象限或第四象限.
故选:B.
点评: 本题考查了点的坐标,求出x、y异号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
4.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有( )
A. 2个 B.3个 C.4个 D. 5个
考点: 坐标与图形性质;三角形的面积.21世纪教育网
分析: 根据点A、B的坐标判断出AB∥x轴,然后根据三角形的面积求出点C到AB的距离,再判断出点C的位置即可.
解答: 解:由图可知,AB∥x轴,且AB=3,
设点C到AB的距离为h,
则△ABC的面积=×3h=3,
解得h=2,
∵点C在第四象限,
∴点C的位置如图所示,共有3个.
故选:B.
点评: 本题考查了坐标与图形性质,三角形面积,判断出AB∥x轴是解题的关键.
5.点P(2,﹣5)关于x轴对称的点的坐标为( )
A. (﹣2,5) B.(2,5) C.(﹣2,﹣5) D. (2,﹣5)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解答: 解:∵点P(2,﹣5)关于x轴对称,
∴对称点的坐标为:(2,5).
故选:B.
点评: 此题主要考查了关于x轴对称点的坐标性质,正确记忆坐标变化规律是解题关键.
6.在平面直角坐标系中,与点(1,2)关于y轴对称的点的坐标是( )
A. (﹣1,2) B.(1,﹣2) C.(﹣1,﹣2) D. (﹣2,﹣1)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答即可.
解答: 解:点(1,2)关于y轴对称的点的坐标是(﹣1,2).
故选A.
点评: 解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
7.如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6),B(﹣6,2),E(2,1),则点D的坐标为( )
A. (﹣4,6) B.(4,6) C.(﹣2,1) D. (6,2)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),进而得出答案.
解答: 解:∵△ABC与△DEF关于y轴对称,A(﹣4,6),
∴D(4,6).
故选:B.
点评: 此题主要考查了关于y轴对称点的性质,准确记忆横纵坐标的关系是解题关键.
8.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )
A. (3,2) B.(2,﹣3) C.(﹣2,3) D. (﹣2,﹣3)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解答: 解:∵点A(2,3),
∴点A关于x轴的对称点的坐标为:(2,﹣3).
故选:B.
点评: 此题主要考查了关于x轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.
9.点A(1,﹣2)关于x轴对称的点的坐标是( )
A. (1,﹣2) B.(﹣1,2) C.(﹣1,﹣2) D. (1,2)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可直接得到答案.
解答: 解:点A(1,﹣2)关于x轴对称的点的坐标是(1,2),
故选:D.
点评: 此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化规律.
二.填空题(共7小题)
10.在平面直角坐标系中,点(﹣4,4)在第 二 象限.
考点: 点的坐标.21世纪教育网
分析: 根据各象限内点的坐标特征解答.
解答: 解:点(﹣4,4)在第二象限.
故答案为:二.
点评: 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
11.点P(﹣2,3)关于x轴的对称点P′的坐标为 (﹣2,﹣3) .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 让点P的横坐标不变,纵坐标互为相反数即可得到点P关于x轴的对称点P′的坐标.
解答: 解:∵点P(﹣2,3)关于x轴的对称点P′,
∴点P′的横坐标不变,为﹣2;纵坐标为﹣3,
∴点P关于x轴的对称点P′的坐标为(﹣2,﹣3).
故答案为:(﹣2,﹣3).
点评: 此题主要考查了关于x轴对称点的性质,用到的知识点为:两点关于x轴对称,横纵坐标不变,纵坐标互为相反数.
12.点P(2, 3)关于x轴的对称点的坐标为 (2,﹣3) .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y)得出即可.
解答: 解:∵点P(2,3)
∴关于x轴的对称点的坐标为:(2,﹣3).
故答案为:(2,﹣3).
点评: 此题主要考查了关于x轴、y轴对称点的性质,正确记忆坐标规律是解题关键.
13.若点M(3,a)关于y轴的对称点是点N(b,2),则(a+b)2014= 1 .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据轴对称的性质,点M和点N的纵坐标相等,横坐标互为相反数,可以求得a、b的值,从而可得a+b的值.
解答: 解:∵点M(3,a)关于y轴的对称点是点N(b,2),
∴b=﹣3,a=2,
∴a+b=﹣1,
∴(a+b)2014=(﹣1)2014=1.
故答案为:1.
点评: 本题考查了轴对称的性质和幂的运算,解题的关键是先求得a、b的值.
14.已知P(1,﹣2),则点P关于x轴的对称点的坐标是 (1,2) .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解答: 解:∵P(1,﹣2),
∴点P关于x轴的对称点的坐标是:(1,2).
故答案为:(1,2).
点评: 此题主要考查了关于x轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.
15.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n= 0 .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”列出方程求解即可.
解答: 解:∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,3=n+5,
解得:m=2,n=﹣2,
∴m+n=0,
故答案为:0.
点评: 本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
16.在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数,若累计到正方形AnBnCnDn时,整点共有1680个,则n= 20 .
考点: 坐标与图形性质;正方形的性质.21世纪教育网
专题: 压轴题;规律型.
分析: 寻找规律:第n个正方形上的整点个数是:4+4(2n﹣1)=8n.得方程求解.
解答: 解:正方形A1B1C1D1上的整点个数是8,
正方形A2B2C2D2上的整点个数是16,
正方形A3B3C3D3上的整点个数是24,
则第n个正方形上的整点个数是:4+4(2n﹣1)=8n.
累计到正方形AnBnCnDn时,整点共有8(1+2+…+n),即8(1+2+…+n)=1680,
=210,解得n1=20,n2=﹣21(舍去).
故答案为:20.
点评: 本题需要通过找每个正方形上的整点个数的规律,得出一般结论,再进一步求和.
三.解答题(共5小题)
17.在平面直角坐标系xOy中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.
(1)点A关于原点O的对称点A′的坐标为 (1,﹣5) ,点B关于x轴的对称点B′的坐标为 (4,﹣2) ,点C关于y轴的对称点C的坐标为 (1,0) .
(2)求(1)中的△A′B′C′的面积.
考点: 关于原点对称的点的坐标;三角形的面积;关于x轴、y轴对称的点的坐标.21世纪教育网
分析: (1)关于原点对称的两点的横、纵坐标都是互为相反数;关于x轴对称的两点的横坐标相同,纵坐标互为相反数;关于y轴对称的两点的横坐标互为相反数,纵坐标相同;
(2)根据点A′(1,﹣5),B′(4,﹣2),C′(1,0)在平面直角坐标系中的位置,可以求得A′C′=5,B′D=3,所以由三角形的面积公式进行解答.
解答: 解:(1)∵A(﹣1,5),
∴点A关于原点O的对称点A′的坐标为(1,﹣5).
∵B(4,2),
∴点B关于x轴的对称点B′的坐标为(4,﹣2).
∵C(﹣1,0),
∴点C关于y轴的对称点C′的坐标为(1,0).
故答案为:(1,﹣5),(4,﹣2),(1,0).
(2)如图,∵A′(1,﹣5),B′(4,﹣2),C′(1,0).
∴A′C′=|﹣5﹣0|=5,B′D=|4﹣1|=3,
∴S△A′B′C′=A′C′?B′D=×5×3=7.5,即(1)中的△A′B′C′的面积是7.5.
点评: 本题考查了关于原点、x轴、y轴对称的点的坐标,三角形的面积.解答(2)题时,充分体现了“数形结合”数学思想的优势.
18.请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(0,2),B点坐标为(﹣2,0);
(2)在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.
考点: 坐标与图形性质;等腰三角形的性质.21世纪教育网
专题: 网格型.
分析: (1)根据A点坐标为(0,2),B点坐标为(﹣2,0),则点A所在的纵线一定是y轴,B所在的横线一定是x轴.
(2)分AB时底边或腰两种情况进行讨论.
解答: 解:(1)在网格中建立平面直角坐标系如图所示:
(2)满足条件的点有4个:C1:(2,0);C2:(,0);C3:(0,0);C4:(,0).
点评: 本题考查了等腰三角形的性质及坐标与图形的性质;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
19.如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
考点: 坐标与图形性质;平行四边形的性质.21世纪教育网
分析: (1)本题应从BC为对角线、AC为对角线、AB为对角线三种情况入手讨论,即可得出第四个点的坐标.
(2)解本题时应将三角形进行分化,化为几个直角三角形的和,解出面积和,乘以2即为平行四边形的面积.
解答: 解:(1)BC为对角线时,第四个点坐标为(7,7);AB为对角线时,第四个点为(5,1);当AC为对角线时,第四个点坐标为(1,5).
(2)图中△ABC面积=3×3﹣(1×3+1×3+2×2)=4,所以平行四边形面积=2×△ABC面积=8.
点评: 此题主要考查了平行四边形的性质和判定,难易程度适中.
20.已知点P(a+1,2a﹣1)关于x轴的对称点在第一象限,求a的取值范围.
考点: 关于x轴、y轴对称的点的坐标;解一元一次不等式组.21世纪教育网
专题: 计算题.
分析: 点P(a+1,2a﹣1)关于x轴的对称点在第一象限,则点P(a+1,2a﹣1)在第四象限,符号为(+,﹣).
解答: 解:依题意得p点在第四象限,
∴,
解得:﹣1<a<,
即a的取值范围是﹣1<a<.
点评: 考查了第一象限的点关于x轴对称的点在第四象限,要学会发散性思考,可以由此题联想到更多的点关于某一坐标轴对称的性质.
21.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
考点: 关于原点对称的点的坐标;等腰三角形的性质.21世纪教育网
专题: 应用题.
分析: (1)根据坐标关于原点对称的特点即可得出点P′的坐标,
(2)要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
解答: 解:(1)点P关于原点的对称点P'的坐标为(2,1);
(2),
(a)动点T在原点左侧,
当时,△P'TO是等腰三角形,
∴点,
(b)动点T在原点右侧,
①当T2O=T2P'时,△P'TO是等腰三角形,
得:,
②当T3O=P'O时,△P'TO是等腰三角形,
得:点,
③当T4P'=P'O时,△P'TO是等腰三角形,
得:点T4(4,0).
综上所述,符合条件的t的值为.
点评: 本题主要考查了平面直角坐标系中坐标关于原点对称的特点,难度适中.
一.选择题(共9小题)
1.在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图的坐标平面上有P、Q两点,其坐标分别为(5,a)、(b,7).根据图中P、Q两点的位置,判断点(6﹣b,a﹣10)落在第几象限?( )
A.一 B.二 C.三 D.四
3.若点M(x,y)满足(x+y)2=x2+y2﹣2,则点M所在象限是( )
A.第一象限或第三象限 B.第二象限或第四象限 C.第一象限或第二象限 D.不能确定
4.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有( )
A.2个 B.3个 C.4个 D.5个
5. 点P(2,﹣5)关于x轴对称的点的坐标为( )
A.(﹣2,5) B.(2,5) C.(﹣2,﹣5) D.(2,﹣5)
6.在平面直角坐标系中,与点(1,2)关于y轴对称的点的坐标是( )
A.(﹣1,2) B.(1,﹣2) C.(﹣1,﹣2) D.(﹣2,﹣1)
7.如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6),B(﹣6,2),E(2,1),则点D的坐标为( )
A.(﹣4,6) B.(4,6) C.(﹣2,1) D.(6,2)
8.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )
A.(3,2) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
9.点A(1,﹣2)关于x轴对称的点的坐标是( )
A.(1,﹣2) B.(﹣1,2) C.(﹣1,﹣2) D.(1,2)
二.填空题(共7小题)
10.在平面直角坐标系中,点(﹣4,4)在第 _________ 象限.
11.点P(﹣2,3)关于x轴的对称点P′的坐标为 _________ .
12.点P(2,3)关于x轴的对称点的坐标为 _________ .
13.若点M(3,a)关于y轴的对称点是点N(b,2),则(a+b)2014= _________ .
14.已知P(1,﹣2),则点P关于x轴的对称点的坐标是 _________ .
15.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n= _________ .
16.在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数,若累计到正方形AnBnCnDn时,整点共有1680个,则n= _________ .
三.解答题(共5小题)
17.在平面直角坐标系xOy中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.
(1)点A关于原点O的对称点A′的坐标为 _________ ,点B关于x轴的对称点B′的坐标为 _________ ,点C关于y轴的对称点C的坐标为 _________ .
(2)求(1)中的△A′B′C′的面积.
18.请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(0,2),B点坐标为(﹣2,0);
(2)在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.
19.如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
20.已知点P(a+1,2a﹣1)关于x轴的对称点在第一象限,求a的取值范围.
21.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
17.2.1平面直角坐标系
参考答案与试题解析
一.选择题(共9小题)
1.在平面直角坐标系中,点M(﹣2,1)在( )
A. 第一象限 B.第二象限 C.第三象限 D. 第四象限
考点: 点的坐标.21世纪教育网
分析: 根据各象限内点的坐标特征解答.
解答: 解:点M(﹣2,1)在第二象限.
故选:B.
点评: 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.如图的坐标平面上有P、Q两点,其坐标分别为(5,a)、(b,7).根据图中P、Q两点的位置,判断点(6﹣b,a﹣10)落在第几象限?( )
A. 一 B.二 C.三 D. 四
考点: 点的坐标.21世纪教育网
分析: 由平面直角坐标系判断出a<7,b<5,然后求出6﹣b,a﹣10的正负情况,再根据各象限内点的坐标特征解答.
解答: 解:∵(5,a)、(b,7),
∴a<7,b<5,
∴6﹣b>0,a﹣10<0,
∴点(6﹣b,a﹣10)在第四象限.
故选D.
点评: 本题考查了点的坐标,观察图形,判断出a、b的取值范围是解题的关键.
3.若点M(x,y)满足(x+y)2=x2+y2﹣2,则点M所在象限是( )
A. 第一象限或第三象限 B. 第二象限或第四象限
C. 第一象限或第二象限 D. 不能确定
考点: 点的坐标;完全平方公式.21世纪教育网
分析: 利用完全平方公式展开得到xy=﹣1,再根据异号得负判断出x、y异号,然后根据各象限内点的坐标特征解答.
解答: 解:∵(x+y)2=x2+2xy+y2,
∴原式可化为xy=﹣1,
∴x、y异号,
∴点M(x,y)在第二象限或第四象限.
故选:B.
点评: 本题考查了点的坐标,求出x、y异号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
4.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有( )
A. 2个 B.3个 C.4个 D. 5个
考点: 坐标与图形性质;三角形的面积.21世纪教育网
分析: 根据点A、B的坐标判断出AB∥x轴,然后根据三角形的面积求出点C到AB的距离,再判断出点C的位置即可.
解答: 解:由图可知,AB∥x轴,且AB=3,
设点C到AB的距离为h,
则△ABC的面积=×3h=3,
解得h=2,
∵点C在第四象限,
∴点C的位置如图所示,共有3个.
故选:B.
点评: 本题考查了坐标与图形性质,三角形面积,判断出AB∥x轴是解题的关键.
5.点P(2,﹣5)关于x轴对称的点的坐标为( )
A. (﹣2,5) B.(2,5) C.(﹣2,﹣5) D. (2,﹣5)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解答: 解:∵点P(2,﹣5)关于x轴对称,
∴对称点的坐标为:(2,5).
故选:B.
点评: 此题主要考查了关于x轴对称点的坐标性质,正确记忆坐标变化规律是解题关键.
6.在平面直角坐标系中,与点(1,2)关于y轴对称的点的坐标是( )
A. (﹣1,2) B.(1,﹣2) C.(﹣1,﹣2) D. (﹣2,﹣1)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答即可.
解答: 解:点(1,2)关于y轴对称的点的坐标是(﹣1,2).
故选A.
点评: 解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
7.如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6),B(﹣6,2),E(2,1),则点D的坐标为( )
A. (﹣4,6) B.(4,6) C.(﹣2,1) D. (6,2)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),进而得出答案.
解答: 解:∵△ABC与△DEF关于y轴对称,A(﹣4,6),
∴D(4,6).
故选:B.
点评: 此题主要考查了关于y轴对称点的性质,准确记忆横纵坐标的关系是解题关键.
8.在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点的坐标为( )
A. (3,2) B.(2,﹣3) C.(﹣2,3) D. (﹣2,﹣3)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解答: 解:∵点A(2,3),
∴点A关于x轴的对称点的坐标为:(2,﹣3).
故选:B.
点评: 此题主要考查了关于x轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.
9.点A(1,﹣2)关于x轴对称的点的坐标是( )
A. (1,﹣2) B.(﹣1,2) C.(﹣1,﹣2) D. (1,2)
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可直接得到答案.
解答: 解:点A(1,﹣2)关于x轴对称的点的坐标是(1,2),
故选:D.
点评: 此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化规律.
二.填空题(共7小题)
10.在平面直角坐标系中,点(﹣4,4)在第 二 象限.
考点: 点的坐标.21世纪教育网
分析: 根据各象限内点的坐标特征解答.
解答: 解:点(﹣4,4)在第二象限.
故答案为:二.
点评: 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
11.点P(﹣2,3)关于x轴的对称点P′的坐标为 (﹣2,﹣3) .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 让点P的横坐标不变,纵坐标互为相反数即可得到点P关于x轴的对称点P′的坐标.
解答: 解:∵点P(﹣2,3)关于x轴的对称点P′,
∴点P′的横坐标不变,为﹣2;纵坐标为﹣3,
∴点P关于x轴的对称点P′的坐标为(﹣2,﹣3).
故答案为:(﹣2,﹣3).
点评: 此题主要考查了关于x轴对称点的性质,用到的知识点为:两点关于x轴对称,横纵坐标不变,纵坐标互为相反数.
12.点P(2, 3)关于x轴的对称点的坐标为 (2,﹣3) .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y)得出即可.
解答: 解:∵点P(2,3)
∴关于x轴的对称点的坐标为:(2,﹣3).
故答案为:(2,﹣3).
点评: 此题主要考查了关于x轴、y轴对称点的性质,正确记忆坐标规律是解题关键.
13.若点M(3,a)关于y轴的对称点是点N(b,2),则(a+b)2014= 1 .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据轴对称的性质,点M和点N的纵坐标相等,横坐标互为相反数,可以求得a、b的值,从而可得a+b的值.
解答: 解:∵点M(3,a)关于y轴的对称点是点N(b,2),
∴b=﹣3,a=2,
∴a+b=﹣1,
∴(a+b)2014=(﹣1)2014=1.
故答案为:1.
点评: 本题考查了轴对称的性质和幂的运算,解题的关键是先求得a、b的值.
14.已知P(1,﹣2),则点P关于x轴的对称点的坐标是 (1,2) .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解答: 解:∵P(1,﹣2),
∴点P关于x轴的对称点的坐标是:(1,2).
故答案为:(1,2).
点评: 此题主要考查了关于x轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.
15.若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n= 0 .
考点: 关于x轴、y轴对称的点的坐标.21世纪教育网
分析: 根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”列出方程求解即可.
解答: 解:∵点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,
∴m+2=4,3=n+5,
解得:m=2,n=﹣2,
∴m+n=0,
故答案为:0.
点评: 本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
16.在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数,若累计到正方形AnBnCnDn时,整点共有1680个,则n= 20 .
考点: 坐标与图形性质;正方形的性质.21世纪教育网
专题: 压轴题;规律型.
分析: 寻找规律:第n个正方形上的整点个数是:4+4(2n﹣1)=8n.得方程求解.
解答: 解:正方形A1B1C1D1上的整点个数是8,
正方形A2B2C2D2上的整点个数是16,
正方形A3B3C3D3上的整点个数是24,
则第n个正方形上的整点个数是:4+4(2n﹣1)=8n.
累计到正方形AnBnCnDn时,整点共有8(1+2+…+n),即8(1+2+…+n)=1680,
=210,解得n1=20,n2=﹣21(舍去).
故答案为:20.
点评: 本题需要通过找每个正方形上的整点个数的规律,得出一般结论,再进一步求和.
三.解答题(共5小题)
17.在平面直角坐标系xOy中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.
(1)点A关于原点O的对称点A′的坐标为 (1,﹣5) ,点B关于x轴的对称点B′的坐标为 (4,﹣2) ,点C关于y轴的对称点C的坐标为 (1,0) .
(2)求(1)中的△A′B′C′的面积.
考点: 关于原点对称的点的坐标;三角形的面积;关于x轴、y轴对称的点的坐标.21世纪教育网
分析: (1)关于原点对称的两点的横、纵坐标都是互为相反数;关于x轴对称的两点的横坐标相同,纵坐标互为相反数;关于y轴对称的两点的横坐标互为相反数,纵坐标相同;
(2)根据点A′(1,﹣5),B′(4,﹣2),C′(1,0)在平面直角坐标系中的位置,可以求得A′C′=5,B′D=3,所以由三角形的面积公式进行解答.
解答: 解:(1)∵A(﹣1,5),
∴点A关于原点O的对称点A′的坐标为(1,﹣5).
∵B(4,2),
∴点B关于x轴的对称点B′的坐标为(4,﹣2).
∵C(﹣1,0),
∴点C关于y轴的对称点C′的坐标为(1,0).
故答案为:(1,﹣5),(4,﹣2),(1,0).
(2)如图,∵A′(1,﹣5),B′(4,﹣2),C′(1,0).
∴A′C′=|﹣5﹣0|=5,B′D=|4﹣1|=3,
∴S△A′B′C′=A′C′?B′D=×5×3=7.5,即(1)中的△A′B′C′的面积是7.5.
点评: 本题考查了关于原点、x轴、y轴对称的点的坐标,三角形的面积.解答(2)题时,充分体现了“数形结合”数学思想的优势.
18.请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(0,2),B点坐标为(﹣2,0);
(2)在x轴上画点C,使△ABC为等腰三角形,请画出所有符合条件的点C,并直接写出相应的C点坐标.
考点: 坐标与图形性质;等腰三角形的性质.21世纪教育网
专题: 网格型.
分析: (1)根据A点坐标为(0,2),B点坐标为(﹣2,0),则点A所在的纵线一定是y轴,B所在的横线一定是x轴.
(2)分AB时底边或腰两种情况进行讨论.
解答: 解:(1)在网格中建立平面直角坐标系如图所示:
(2)满足条件的点有4个:C1:(2,0);C2:(,0);C3:(0,0);C4:(,0).
点评: 本题考查了等腰三角形的性质及坐标与图形的性质;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.
19.如图,A、B、C为一个平行四边形的三个顶点,且A、B、C三点的坐标分别为(3,3)、(6,4)、(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.
考点: 坐标与图形性质;平行四边形的性质.21世纪教育网
分析: (1)本题应从BC为对角线、AC为对角线、AB为对角线三种情况入手讨论,即可得出第四个点的坐标.
(2)解本题时应将三角形进行分化,化为几个直角三角形的和,解出面积和,乘以2即为平行四边形的面积.
解答: 解:(1)BC为对角线时,第四个点坐标为(7,7);AB为对角线时,第四个点为(5,1);当AC为对角线时,第四个点坐标为(1,5).
(2)图中△ABC面积=3×3﹣(1×3+1×3+2×2)=4,所以平行四边形面积=2×△ABC面积=8.
点评: 此题主要考查了平行四边形的性质和判定,难易程度适中.
20.已知点P(a+1,2a﹣1)关于x轴的对称点在第一象限,求a的取值范围.
考点: 关于x轴、y轴对称的点的坐标;解一元一次不等式组.21世纪教育网
专题: 计算题.
分析: 点P(a+1,2a﹣1)关于x轴的对称点在第一象限,则点P(a+1,2a﹣1)在第四象限,符号为(+,﹣).
解答: 解:依题意得p点在第四象限,
∴,
解得:﹣1<a<,
即a的取值范围是﹣1<a<.
点评: 考查了第一象限的点关于x轴对称的点在第四象限,要学会发散性思考,可以由此题联想到更多的点关于某一坐标轴对称的性质.
21.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
考点: 关于原点对称的点的坐标;等腰三角形的性质.21世纪教育网
专题: 应用题.
分析: (1)根据坐标关于原点对称的特点即可得出点P′的坐标,
(2)要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
解答: 解:(1)点P关于原点的对称点P'的坐标为(2,1);
(2),
(a)动点T在原点左侧,
当时,△P'TO是等腰三角形,
∴点,
(b)动点T在原点右侧,
①当T2O=T2P'时,△P'TO是等腰三角形,
得:,
②当T3O=P'O时,△P'TO是等腰三角形,
得:点,
③当T4P'=P'O时,△P'TO是等腰三角形,
得:点T4(4,0).
综上所述,符合条件的t的值为.
点评: 本题主要考查了平面直角坐标系中坐标关于原点对称的特点,难度适中.
