冀教版七年级数学上册3.3 代数式的值 课件(共31张PPT)
文档属性
| 名称 | 冀教版七年级数学上册3.3 代数式的值 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 00:00:00 | ||
图片预览











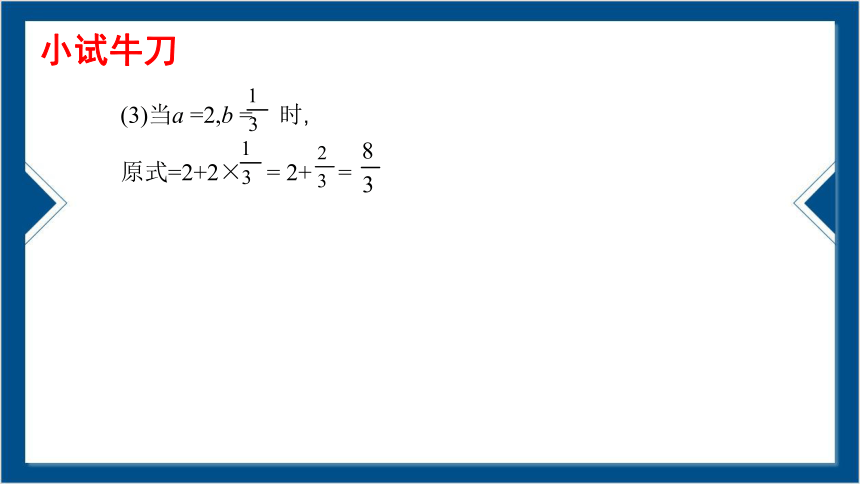
文档简介
(共31张PPT)
3.3 代数式的值
第三章 代数式
学习目标
1.会求代数式的值;
? 2.掌握代数式的值的概念,能用具体数值代替代数式中的字母,求出代数式的值;
3.在解决实际问题的过程中,感受两个量之间的对应关系,进一步发展符号意识.
新课导入
由三种图示方法得到空心矩阵的总点数分别为
4n-4,4(n-1),2n+2(n-2).请你谈谈当n时具体数值的时候,
能算出这个空心方阵的总点数吗?
求代数式的值
感悟新知
1
(1)当n取4, 10, 13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值.
n=4时,4×4-4=12
n=10时,4×10-4=36
n=13时,4×13-4=48
n=25时,4×25-4=96
(2)对于n的同一个值,同学们得到的结果都相同吗?
相同
总结:从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代数式相应的值.
感悟新知
一个代数式,可以看做一个计算程序.
例如:
5x2-8x+2
输入x=-2
5×(-2)x2-8×(-2)+2
输出38
感悟新知
问 题
1. 按上面的程序,计算x=3,x=6时的输出值.
2. 任意取x的两个值,请同桌的同学完成上面的求
值过程,并相互检查求值过程和结果是否正确.
感悟新知
定义:一般地,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值.这个过程叫做求代数式的值.
感悟新知
注:
1. 代入数值时不要代错,特别是代数式里有多个字母时,要注意“对号入座”;
2. 代数式不是最简形式时,可先化简代数式,再代入数值求值;
3. 代数式里原来省略的乘号,代入数值时必须添上.
感悟新知
根据下面a,b的值,求代数式 的值.
(1) a=2,b=-6; (2) a=-10,b=4.
解:(1)当 a=2,b=-6时,
(2)当 a=-10,b=4时,
例 1
小试牛刀
1.当a=2,b= 时,求下列各代数式的值:
(1)a(a+b); (2) ; (3)a+ab.
解:(1) 当a=2,b= 时,
原式=2×(2+ )=2 × =
(2)当a=2,b= 时,
原式= =4+ =
(3)当a =2,b = 时,
原式=2+2× = 2+ =
小试牛刀
2.当x=,y=-5时,代数式2x2-y的值为_______.
解:当x=,y=-5时,
原式=2×() 2-(-5)=2×+5=.
小试牛刀
总 结
用直接代入法求代数式的值可以分三步:
①“当……时”,即指出字母的值;
②“原式=……”,即代入所给字母的值;
③ 计算.
例2:已知长方体的高为h,底面是边长为a的正方形.当h=3,a=2时,分别求其体积V和表面积S.
【2023·石家庄外国语学校月考】
(1)当a=-,b= 时,求下列代数式的值:
①(a+b)2;
②a2+2ab+b2.
3.
(2)回答下列问题:
①(1)中两个代数式的值有什么关系?
②当a=2,b=-3时,上述结论是否仍然成立?
解:相等.
当a=2,b=-3时,
(a+b)2=(2-3)2=1,
a2+2ab+b2=22+2×2×(-3)+(-3)2=1,
所以结论仍然成立.
③你能用简便的方法算出当a=-0.875,b=-0.125时,代数式a2+2ab+b2的值吗?
能.当a=-0.875,b=-0.125时,
a2+2ab+b2=(a+b)2=(-0.875-0.125)2=1.
感悟新知
整体代入求代数式的值
2
例3
当代数式x2+3x+5的值为9时,求代数式3x2+9x-3的值.
解:由代数式x2+3x+5的值为9,得x2+3x=4,
所以3x2+9x-3=3(x2+3x)-3=3×4-3=9.
感悟新知
总 结
用整体代入法求代数式的值的方法:给出一个含字母的代数式的值,当单个字母的值不能或不容易求出时,一般对给出的代数式或要求值的代数式进行适当变形,通过整体代入,实现快速求值.
4.已知代数式14x+5-21x2的值是-2,求6x2-4x+5的值.
解:因为14x+5-21x2的值是-2,
所以14x-21x2=-7,即2x-3x2=-1.
所以3x2-2x=1.
所以6x2-4x+5=2×(3x2-2x)+5=7.
小试牛刀
小试牛刀
程序计算求代数式的值
1.当a=2,b=1,c=3时代数式c-(c-a)(c-b)的值是( )
A.1 B. 2 C.3 D. 4
2.如果2a+3b=5,那么4a+6b-7=___.
3
A
3.根据如图所示的程序计算,若输入x的值为-1,则输出y的值为________.
4
感悟新知
总 结
解答本题的关键是弄清楚给出的计算程序,利用转化思想求解.
感悟新知
实际应用求代数式的值
4
已知某林场现有的木材蓄积量为a m3,预计今后两年的木材蓄积量的年平均增长率为p%,那么两年后该林场的木材蓄积量将达到多少立方米?若a=2 000,p=10,则两年后该林场的木材蓄积量将达到多少立方米?
例4
解:由题意得,一年后该林场的木材蓄积量为a(1+p%)m3,两年后该林场的木材蓄积量为a(1+p%)(1+p%)m3.
当a=2 000,p=10时,a(1+p%)(1+p%)=2 000×(1+10%)×(1+10%)=2 420 .
故两年后该林场的木材蓄积量将达到a(1+p%)(1+p%)m3.若a=2 000,p=10,则两年后该林场的木材蓄积量将达到2 420 m3.
总 结
本题运用了转化思想.把实际要解决的问题转化
为求代数式的值的问题.
1.某种摩托车的行车里程与耗油量有如下关系:
(1)用x表示耗油量,用y表示行车里程,请用含x的代数式表示y;
(2)行车里程为210 km时,耗油量是多少?
(3)如果耗油量为2.7 L,可行多少千米?
行车里程/km 60 120 180 …
耗油量/L 1 2 3 …
解:(1)y=60x.
(2)当y=210时,210=60x,x=3.5.
即行车里程为210 km时,耗油量是3.5 L.
(3)当x=2.7时,y=60×2.7=162.即耗油量为2.7 L时,可行162 km.
2.【中考·天水】有一根40 cm的金属棒,欲将其截成x根7 cm的小段和y根9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=4,y=1
C.x=3,y=2 D.x=2,y=3
C
课堂小结
同学们,通过本节课的学习,你有什么收获呢?
1.代数式的值得定义;
2.求代数式的值得步骤:①先代入,再计算;②先化简,再代入计算.
3.3 代数式的值
第三章 代数式
学习目标
1.会求代数式的值;
? 2.掌握代数式的值的概念,能用具体数值代替代数式中的字母,求出代数式的值;
3.在解决实际问题的过程中,感受两个量之间的对应关系,进一步发展符号意识.
新课导入
由三种图示方法得到空心矩阵的总点数分别为
4n-4,4(n-1),2n+2(n-2).请你谈谈当n时具体数值的时候,
能算出这个空心方阵的总点数吗?
求代数式的值
感悟新知
1
(1)当n取4, 10, 13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值.
n=4时,4×4-4=12
n=10时,4×10-4=36
n=13时,4×13-4=48
n=25时,4×25-4=96
(2)对于n的同一个值,同学们得到的结果都相同吗?
相同
总结:从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代数式相应的值.
感悟新知
一个代数式,可以看做一个计算程序.
例如:
5x2-8x+2
输入x=-2
5×(-2)x2-8×(-2)+2
输出38
感悟新知
问 题
1. 按上面的程序,计算x=3,x=6时的输出值.
2. 任意取x的两个值,请同桌的同学完成上面的求
值过程,并相互检查求值过程和结果是否正确.
感悟新知
定义:一般地,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值.这个过程叫做求代数式的值.
感悟新知
注:
1. 代入数值时不要代错,特别是代数式里有多个字母时,要注意“对号入座”;
2. 代数式不是最简形式时,可先化简代数式,再代入数值求值;
3. 代数式里原来省略的乘号,代入数值时必须添上.
感悟新知
根据下面a,b的值,求代数式 的值.
(1) a=2,b=-6; (2) a=-10,b=4.
解:(1)当 a=2,b=-6时,
(2)当 a=-10,b=4时,
例 1
小试牛刀
1.当a=2,b= 时,求下列各代数式的值:
(1)a(a+b); (2) ; (3)a+ab.
解:(1) 当a=2,b= 时,
原式=2×(2+ )=2 × =
(2)当a=2,b= 时,
原式= =4+ =
(3)当a =2,b = 时,
原式=2+2× = 2+ =
小试牛刀
2.当x=,y=-5时,代数式2x2-y的值为_______.
解:当x=,y=-5时,
原式=2×() 2-(-5)=2×+5=.
小试牛刀
总 结
用直接代入法求代数式的值可以分三步:
①“当……时”,即指出字母的值;
②“原式=……”,即代入所给字母的值;
③ 计算.
例2:已知长方体的高为h,底面是边长为a的正方形.当h=3,a=2时,分别求其体积V和表面积S.
【2023·石家庄外国语学校月考】
(1)当a=-,b= 时,求下列代数式的值:
①(a+b)2;
②a2+2ab+b2.
3.
(2)回答下列问题:
①(1)中两个代数式的值有什么关系?
②当a=2,b=-3时,上述结论是否仍然成立?
解:相等.
当a=2,b=-3时,
(a+b)2=(2-3)2=1,
a2+2ab+b2=22+2×2×(-3)+(-3)2=1,
所以结论仍然成立.
③你能用简便的方法算出当a=-0.875,b=-0.125时,代数式a2+2ab+b2的值吗?
能.当a=-0.875,b=-0.125时,
a2+2ab+b2=(a+b)2=(-0.875-0.125)2=1.
感悟新知
整体代入求代数式的值
2
例3
当代数式x2+3x+5的值为9时,求代数式3x2+9x-3的值.
解:由代数式x2+3x+5的值为9,得x2+3x=4,
所以3x2+9x-3=3(x2+3x)-3=3×4-3=9.
感悟新知
总 结
用整体代入法求代数式的值的方法:给出一个含字母的代数式的值,当单个字母的值不能或不容易求出时,一般对给出的代数式或要求值的代数式进行适当变形,通过整体代入,实现快速求值.
4.已知代数式14x+5-21x2的值是-2,求6x2-4x+5的值.
解:因为14x+5-21x2的值是-2,
所以14x-21x2=-7,即2x-3x2=-1.
所以3x2-2x=1.
所以6x2-4x+5=2×(3x2-2x)+5=7.
小试牛刀
小试牛刀
程序计算求代数式的值
1.当a=2,b=1,c=3时代数式c-(c-a)(c-b)的值是( )
A.1 B. 2 C.3 D. 4
2.如果2a+3b=5,那么4a+6b-7=___.
3
A
3.根据如图所示的程序计算,若输入x的值为-1,则输出y的值为________.
4
感悟新知
总 结
解答本题的关键是弄清楚给出的计算程序,利用转化思想求解.
感悟新知
实际应用求代数式的值
4
已知某林场现有的木材蓄积量为a m3,预计今后两年的木材蓄积量的年平均增长率为p%,那么两年后该林场的木材蓄积量将达到多少立方米?若a=2 000,p=10,则两年后该林场的木材蓄积量将达到多少立方米?
例4
解:由题意得,一年后该林场的木材蓄积量为a(1+p%)m3,两年后该林场的木材蓄积量为a(1+p%)(1+p%)m3.
当a=2 000,p=10时,a(1+p%)(1+p%)=2 000×(1+10%)×(1+10%)=2 420 .
故两年后该林场的木材蓄积量将达到a(1+p%)(1+p%)m3.若a=2 000,p=10,则两年后该林场的木材蓄积量将达到2 420 m3.
总 结
本题运用了转化思想.把实际要解决的问题转化
为求代数式的值的问题.
1.某种摩托车的行车里程与耗油量有如下关系:
(1)用x表示耗油量,用y表示行车里程,请用含x的代数式表示y;
(2)行车里程为210 km时,耗油量是多少?
(3)如果耗油量为2.7 L,可行多少千米?
行车里程/km 60 120 180 …
耗油量/L 1 2 3 …
解:(1)y=60x.
(2)当y=210时,210=60x,x=3.5.
即行车里程为210 km时,耗油量是3.5 L.
(3)当x=2.7时,y=60×2.7=162.即耗油量为2.7 L时,可行162 km.
2.【中考·天水】有一根40 cm的金属棒,欲将其截成x根7 cm的小段和y根9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=4,y=1
C.x=3,y=2 D.x=2,y=3
C
课堂小结
同学们,通过本节课的学习,你有什么收获呢?
1.代数式的值得定义;
2.求代数式的值得步骤:①先代入,再计算;②先化简,再代入计算.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
