高中数学人教A版(2019)必修2 第十章 概率综合卷 解答题专项章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 第十章 概率综合卷 解答题专项章节综合练习题(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 675.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 11:03:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十章 概率综合卷 解答题专项
一、解答题
1.投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏.假设甲、乙、丙、丁是四位投壶游戏参与者,且甲、乙、丙每次投壶时,投中与不投中的机会是均等的,丁每次投壶时,投中的概率为.甲、乙、丙、丁每人每次投壶是否投中相互独立,互不影响.
(1)若甲、乙、丙、丁每人各投壶1次,求只有一人投中的概率;
(2)甲、丁进行投壶比赛,若甲、丁每人各投壶2次,投中次数多者获胜,求丁获胜的概率.
2.甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为,甲、乙都闯关成功的频率为,乙、丙都闯关成功的概率为,每人闯关成功记2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
3.(2023高三上·吉林开学考)甲乙两所友好学校举行篮球联谊赛,先获得3场比赛胜利的学校获得冠军并终止比赛,比赛交替在甲校与乙校进行,第一场比赛在甲校进行.已知甲队在主场(甲校)获胜的概率为,在客场(乙校)获胜的概率为,每场比赛要分出胜负且胜负概率不变.
(1)求甲队以3胜1负的成绩赢得冠军的概率;
(2)设篮球联谊赛比赛进行的场数为X,求随机变量X的分布列与期望.
4.(2023高一下·楚雄期末)袋中装有大小完全相同的6个红球,3个蓝球,其中有2个红球和1个蓝球上面标记了数字1,其他球标记了数字2.
(1)每次有放回地任取1个小球,连续取两次,求取出的2个球恰有1个红球且两球的数字和为3的概率;
(2)从袋中不放回地依次取2个小球,每次取1个,记事件第一次取到的是红球,事件第二次取到了标记数字1的球,求,并判断事件与事件是否相互独立.
5.已知1个不秀明的袋子中装有6个白球和4个黄球(这些球除颜色外无其他差异).甲从袋中摸出1球,若摸出的是白球,则除将摸出的白球放回袋子中外,再将袋子中的1个黄球拿出,放入1个白球;若摸出的是黄球,则除将摸出的黄球放回袋子中外,再将袋子中的1个白球拿出,放人1个黄球.再充分搅拌均匀后,进行第二次摸球,依此类推,直到袋中全部是同一种颜色的球,已知甲进行了4次摸球.
(1)求袋子中球的颜色只有一种的概率;
(2)求袋子中白球个数为4的概率.
6.(2024高三上·硚口)有编号为1,2,3,...,18,19,20的20个箱子,第一个箱子有2个黄球1个绿球,其余箱子均为2个黄球2个绿球,现从第一个箱子中取出一个球放入第二个箱子,再从第二个箱子中取出一个球放入第三个箱子,以此类推,最后从第19个箱子取出一个球放入第20个箱子,记为从第个箱子中取出黄球的概率.
(1)求;
(2)求.
7.(2023高一下·苏州期末)已知甲的投篮命中率为0.6,乙的投篮命中率为0.7,丙的投篮命中率为0.5.
(1)甲、乙、丙各投篮一次,求甲和乙命中,丙不命中的概率;
(2)甲、乙、丙各投篮一次,求恰有一人命中的概率;
(3)甲、乙、丙各投篮一次,求至少有一人命中的概率.
8.(2023高一下·湖南期末)某学校组织人工智能知识竞赛,在初赛中有两轮答题,第一轮从A类的4个问题中随机抽取3题作答,每答对1题得20分,答错得0分;第二轮从B类分值分别为10,20,30的3个问题中随机抽取2题作答,每答对1题该题得满分,答错得0分.若两轮总积分不低于90分则晋级复赛.甲、乙同时参赛,在A类的4个问题中,甲每个问题答对的概率为,乙只能答对3个问题;在B类3个分值分别为10,20,30的问题中,甲答对的概率分别为1,,,乙答对的概率分别为,,.甲、乙回答任一问题正确与否互不影响.
(1)分别求甲、乙在第一轮得最高分的概率;
(2)谁晋级复赛的概率更大?请说明理由.
9.(2023高一下·河南月考)大学毕业生小张和小李通过了某单位的招聘笔试考试,正在积极准备结构化面试,每天相互进行多轮测试,每轮由小张和小李各回答一个问题,已知小张每轮答对的概率为,小李每轮答对的概率为.在每轮活动中,小张和小李答对与否互不影响,各轮结果也互不影响.
(1)求两人在两轮活动中都答对的概率;
(2)求两人在两轮活动中至少答对3道题的概率;
(3)求两人在三轮活动中,小张和小李各自答对题目的个数相等且至少为2的概率.
10.(2023高一下·达州期末)某超市将若干个问题印在质地、大小相同的小球上,顾客每次随机抽出个小球并回答上面的问题.若顾客第一次答对,则获得购物券并结束活动:若顾客第一次答错,就再抽一次,答对获得购物券并结束活动,答错结束活动.顾客对不同题目的回答是独立的.
(1)顾客乙答对每道题目的概率为,若无放回的抽取,求乙获得购物券的概率:
(2)顾客丙首次答对每道题目的概率为,对相同题目答对的概率为.若有放回的抽取,顾客丙第二次抽到相同题目的概率为,求丙第二次获得购物券的概率.
11.(2023高一下·莲湖期末)某学校派甲、乙两人组成“少年队”参加射击比赛,每轮比赛由甲、乙各射击一次,已知甲每轮射中的概率为,乙每轮射中的概率为.在每轮比赛中,甲和乙射中与否互不影响,各轮比赛结果也互不影响.
(1)求“少年队”在一轮比赛中恰好射中1次的概率;
(2)求“少年队”在三轮比赛中恰好射中3次的概率.
12.(2023高一下·海南期末)在如图所示的电路中,、、、四个开关闭合的概率分别为、、、,且各个开关是否闭合是相互独立的.
(1)求四个开关均断开的概率;
(2)求电路为通路的概率
13.(2023高一下·荔湾期末)某品牌计算机售后保修期为1年,根据大量的维修记录资料,这种品牌的计算机在使用一年内维修次数最多的是3次,其中维修1次的占15%,维修2次的占6%,维修3次的占4%.
(1)若某人购买1台这种品牌的计算机,求下列事件的概率:A=“在保修期内需要维修”;B=“在保修期内维修不超过1次”;
(2)若某人购买2台这种品牌的计算机,2台计算机在保修期内是否需要维修互不影响,求这2台计算机保修期内维修次数总和不超过2次的概率.
14.(2023高一下·广州期末)甲、乙两人参加猜成语活动,每轮活动由甲、乙各猜一个成语,已知甲每轮猜对的概率为,乙每轮猜对的概率为.在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响.
(1)求经过两轮活动,两人共猜对2个成语的概率;
(2)求经过两轮活动,两人猜对成语的个数不相同的概率.
15.(2023高二下·嘉定期末)某校高二年级一个班有60名学生,将期中考试的数学成绩(均为整数)分成六段:,得到如图所示的频率分布直方图,
(1)求的值;
(2)用分层随机抽样的方法从中抽取一个容量为20的样本,已知甲同学的成绩在,乙同学的成绩在,求甲乙至少一人被抽到的概率.
16.(2023高一下·余姚期末)为了纪念2017年在德国波恩举行的联合国气候大会,某社区举办《“环保我参与”有奖问答比赛》活动.某场比赛中,甲、乙、丙三个家庭同时回答一道有关环保知识的问题.已知甲家庭回答正确这道题的概率是,甲、丙两个家庭都回答错误的概率是,乙、丙两个家庭都回答正确的概率是.若各家庭回答是否正确互不影响.
(1)求乙、丙两个家庭各自回答正确这道题的概率;
(2)求甲、乙、丙三个家庭中不少于2个家庭回答正确这道题的概率.
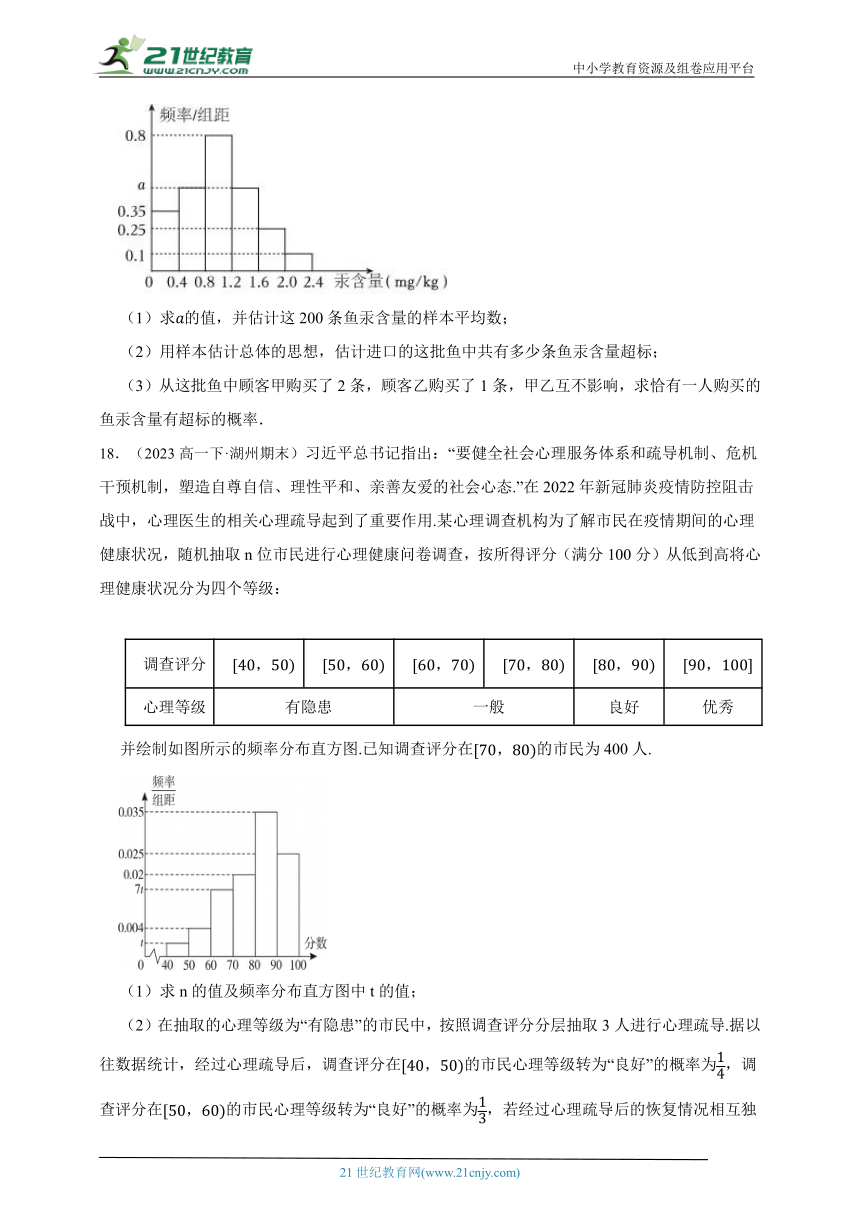
17.(2023高一下·温州期末) 现行国家标准中规定了10大类食品中重金属汞的污染限量值,其中肉食性鱼类及其制品中汞的最大残留量为,近日某水产市场进口了一批冰鲜鱼2000条,从中随机抽取了200条鱼作为样本,检测鱼体汞含量与其体重的比值,由测量结果制成如图所示的频率分布直方图.
(1)求的值,并估计这200条鱼汞含量的样本平均数;
(2)用样本估计总体的思想,估计进口的这批鱼中共有多少条鱼汞含量超标;
(3)从这批鱼中顾客甲购买了2条,顾客乙购买了1条,甲乙互不影响,求恰有一人购买的鱼汞含量有超标的概率.
18.(2023高一下·湖州期末)习近平总书记指出:“要健全社会心理服务体系和疏导机制、危机干预机制,塑造自尊自信、理性平和、亲善友爱的社会心态.”在2022年新冠肺炎疫情防控阻击战中,心理医生的相关心理疏导起到了重要作用.某心理调查机构为了解市民在疫情期间的心理健康状况,随机抽取n位市民进行心理健康问卷调查,按所得评分(满分100分)从低到高将心理健康状况分为四个等级:
调查评分
心理等级 有隐患 一般 良好 优秀
并绘制如图所示的频率分布直方图.已知调查评分在的市民为400人.
(1)求n的值及频率分布直方图中t的值;
(2)在抽取的心理等级为“有隐患”的市民中,按照调查评分分层抽取3人进行心理疏导.据以往数据统计,经过心理疏导后,调查评分在的市民心理等级转为“良好”的概率为,调查评分在的市民心理等级转为“良好”的概率为,若经过心理疏导后的恢复情况相互独立,试问在抽取的3人中,经过心理疏导后,至少有一人心理等级转为“良好”的概率为多少?
(3)心理调查机构与该市管理部门设定的预案是:以抽取的样本作为参考,若市民心理健康指数平均值不低于0.8,则只需发放心理指导资料,否则需要举办心理健康大讲堂.根据你所学的统计知识,判断该市是否需要举办心理健康大讲堂,并说明理由.
注:每组数据以区间的中点值代替,心理健康指数=问卷调查评分/100.
19.(2023高三下·玉林模拟)年月日,中国疾控中心成功分离中国首株新型冠状病毒毒种,月日时分,重组新冠疫苗获批启动临床试验.月日,中国新冠病毒疫苗进入期临床试验截至月日,全球当前有大约种候选新冠病毒疫苗在研发中,其中至少有种疫苗正处于临床试验阶段现有、、三个独立的医疗科研机构,它们在一定时期内能研制出疫苗的概率分别是、、.求:
(1)他们都研制出疫苗的概率;
(2)他们都失败的概率;
(3)他们能够研制出疫苗的概率.
20.(2023高二下·普宁月考)某大学为调研学生在,两家餐厅用餐的满意度,从在,两家餐厅都用过餐的学生中各随机抽取了200人,每人分别对这两家餐厅进行评分,满分为60分.整理评分数据,将分数分成6组:,,,,,,得到餐厅分数的频率分布直方图和餐厅分数的频数分布表:
餐厅分数的频数分布表:
分数区间 频数
4
6
10
30
80
70
定义学生对餐厅评价的“满意度指数”如下:
分数
满意度指数 3 4 5
(1)在抽样的200人中,求对餐厅评价“满意度指数”为4的人数;
(2)从该校在,两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率;
(3)如果从,两家餐厅中选择一家用餐,从期望的角度你会选择哪一家?并说明理由.
21.(2023高二下·浙江期中)从10名同学(其中6女4男)中随机选出3人参加测验,每个女同学通过测验的概率均为,每个男同学通过测验的概率均为,求:
(1)选出的3个同学中,至少有一个男同学的概率;
(2)10个同学中的女同学甲和男同学乙同时被选中且通过测验的概率.
22.(2023·湛江模拟)现有A,B两个广西旅行社,统计了这两个旅行社的游客去漓江、乐满地主题乐园、西街、龙脊梯田四个景点旅游的各240人次的数据,并分别绘制出这两个旅行社240人次分布的柱形图,如图所示.假设去漓江、乐满地主题乐园、西街、龙脊梯田旅游每人次的平均消费分别为1200元、1000元、600元、200元.
(1)通过计算,比较这两个旅行社240人次的消费总额哪个更大;
(2)若甲和乙分别去A旅行社、B旅行社,并都从这四个景点中选择一个去旅游,以这240人次去漓江的频率为概率,求甲、乙至少有一人去漓江的概率.
23.(2023·株洲模拟)2023年亚运会在中国杭州举办,开幕式门票与其他赛事门票在网上开始预定,亚奥理事会规定:开幕式门票分为A、B两档,当预定A档未成功时,系统自动进入B档预定,已知获得A档门票的概率是,若未成功,仍有的概率获得B档门票的机会;而成功获得其他赛事门票的概率均为,且获得每张门票之间互不影响.甲预定了一张A档开幕式门票,一张赛事门票;乙预定了两张赛事门票.
(1)求甲乙两人都没有获得任何门票的概率;
(2)求乙获得的门票数比甲多的概率.
24.(2023·张家界模拟)2022年底,新冠病毒肆虐全国,很多高三同学也都加入羊羊行列.某校参加某次大型考试时采用了线上考试和线下考试两种形式.现随机抽取200名同学的数学成绩做分析,其中线上人数占40%,线下人数占60%,通过分别统计他们的数学成绩得到了如下两个频率分部直方图:
其中称为合格,称为中等,称为良好,称为优秀,称为优异.
(1)根据频率分布直方图,求这200名学生的数学平均分(同一组数据可取该组区间的中点值代替);
(2)现从这200名学生中随机抽取一名同学的数学成绩为良好,试分析他是来自线上考试的可能性大,还是来自线下考试的可能性大.
(3)现从线下考试的学生中随机抽取10名同学,且抽到k个学生的数学成绩为中等的可能性最大,试求k的值.
25.(2023·重庆市模拟)某网络在平台开展了一项有奖闯关活动,并对每一关根据难度进行赋分,竞猜活动共五关,规定:上一关不通过则不进入下一关,本关第一次未通过有再挑战一次的机会,两次均未通过,则闯关失败,且各关能否通过相互独立,已知甲、乙、丙三人都参加了该项活动.
附:若随机变量,则;;.
(1)若甲第一关通过的概率为,第二关通过的概率为,求甲可以进入第三关的概率;
(2)已知该闯关活动累计得分服从正态分布,且满分为450分,现要根据得分给共2500名参加者中得分前400名发放奖励,
①假设该闯关活动平均分数为171分,351分以上共有57人,已知甲的得分为270分,问甲能否获得奖励,请说明理由;
②丙得知他的分数为430分,而乙告诉丙:“这次闯关活动平均分数为201分,351分以上共有57人”,请结合统计学知识帮助丙辨别乙所说信息的真伪.
26.(2023·蚌埠模拟)有研究显示,人体内某部位的直径约的结节约有0.2%的可能性会在1年内发展为恶性肿瘤.某医院引进一台检测设备,可以通过无创的血液检测,估计患者体内直径约的结节是否会在1年内发展为恶性肿瘤,若检测结果为阳性,则提示该结节会在1年内发展为恶性肿瘤,若检测结果为阴性,则提示该结节不会在1年内发展为恶性肿瘤.这种检测的准确率为85%,即一个会在1年内发展为恶性肿瘤的患者有85%的可能性被检出阳性,一个不会在1年内发展为恶性肿瘤的患者有85%的可能性被检出阴性.患者甲被检查出体内长了一个直径约的结节,他做了该项无创血液检测.
(1)求患者甲检查结果为阴性的概率;
(2)若患者甲的检查结果为阴性,求他的这个结节在1年内发展为恶性肿瘤的概率(结果保留5位小数);
(3)医院为每位参加该项检查的患者缴纳200元保险费,对于检测结果为阴性,但在1年内发展为恶性肿瘤的患者,保险公司赔付该患者20万元,若每年参加该项检查的患者有1000人,请估计保险公司每年在这个项目上的收益.
27.某射击运动员为备战奥运会,在相同条件下进行射击训练,结果如下:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率 0.8 0.95 0.88 0.92 0.89 0.91
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗?
(4)假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?
28.某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖规则如下:1、抽奖方案有以下两种:方案,从装有1个红球、2个白球仅颜色不同的甲袋中随机摸出1个球,若是红球,则获得奖金15元,否则,没有奖金,兑奖后将摸出的球放回甲袋中;方案,从装有2个红、1个白球仅颜色不同的乙袋中随机摸出1个球,若是红球,则获得奖金10元,否则,没有奖金,兑奖后将摸出的球放回乙袋中.2.抽奖条件是:顾客购买商品的金额满100元,可根据方案抽奖一;满足150元,可根据方案抽奖例如某顾客购买商品的金额为310元,则该顾客采用的抽奖方式可以有以下三种,根据方案抽奖三次或方案抽奖两次或方案,各抽奖一次已知顾客在该商场购买商品的金额为250元.
(1)若顾客只选择根据方案进行抽奖,求其所获奖金为15元的概率;
(2)当若顾客采用每种抽奖方式的可能性都相等,求其最有可能获得的奖金数(0元除外.
29.(2023高二上·湖北月考)甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为各局比赛的结果都相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)求前4局中乙恰好当1次裁判概率.
30.(2023高二上·佛山期末)每年的11月9日是我国的全国消防日.119为我国规定的统一火灾报警电话,但119台不仅仅是一部电话,也是一套先进的通讯系统.它可以同中国国土上任何一个地方互通重大灾害情报,还可以通过卫星调集防灾救援力量,向消防最高指挥提供火情信息.佛山某中学为了加强学生的消防安全意识,防范安全风险,特在11月9日组织消防安全系列活动.甲、乙两人组队参加消防安全知识竞答活动,每轮竞答活动由甲、乙各答一题.在每轮竞答中,甲和乙答对与否互不影响,各轮结果也互不影响.已知甲每轮答对的概率为,乙每轮答对的概率为,且甲、乙两人在两轮竞答活动中答对3题的概率为.
(1)求的值;
(2)求甲、乙两人在三轮竞答活动中答对4题的概率.
答案解析部分
1.【答案】(1)解:设甲、乙、丙、丁各自在一次投壶中投中分别记为事件A,B,C,D,
则,.
设只有一人投中为事件E,则
.
(2)解:若甲投中0次,则丁至少投中1次;若甲投中1次,则丁投中2次.
设丁获胜为事件M,则.
【解析】【分析】(1) 设甲、乙、丙、丁各自在一次投壶中投中分别记为事件A,B,C,D,则,,然后根据独立事件乘法公式计算即可得解;
(2)分情况讨论,甲投中0次,则丁至少投中1次;若甲投中1次,则丁投中2次.根据独立重复事件公式计算即可得解.
2.【答案】(1)解:三人各自独立闯关,其中甲闯关成功的概率为,
甲、乙都闯关成功的概率为,乙、丙都闯关成功的概率为,
设乙闯关成功的概率为,丙闯关成功的概率为,
∵乙丙独立闯关,
根据独立事件同时发生的概率公式得:.
解得,.
即乙闯关成功的概率为,丙闯关成功的概率为.
(2)解:团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为4分”为事件A,
则,
即团体总分为4分的概率为.
(3)解:团体总分不小于4分,即团体总分为4分或6分,设“团体总分不小于4分”为事件B,
由(2)知团体总分为4分的概率为,
团体总分为6分,即3人都闯关成功的概率为.
所以参加复赛的概率为.
即该小组参加复赛的概率为.
【解析】【分析】 (1)设乙闯关成功的概率为,丙闯关成功的概率为, 结合独立事件概率乘法公式运算求解;
(2)由题意可知: 团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关,结合互斥事件概率和独立事件概率乘法公式运算求解;
(3) 若团体总分不小于4分,则团体总分为4分或6分,结合互斥事件概率和独立事件概率乘法公式运算求解.
3.【答案】(1)解:设事件A为:“甲队以3胜1负的成绩赢得冠军”,
则.
(2)解:由题意:X的可能取值为3,4,5.
则,,
,故随机变量X的分布列为:
X 3 4 5
P
则.
【解析】【分析】(1) 甲队以3胜1负的成绩赢得冠军 ,讨论甲队输球的可能场次,结合独立事件概率乘法公式运算求解;
(2)分析可知 X的可能取值为3,4,5,结合题意求分布列和期望.
4.【答案】(1)解:第一次取到的是红球,第二次取到的是蓝球且两球的数字和为3,即抽到红1蓝2或者红2蓝1的概率:,
第一次取到的是蓝球,第二次取到的是红球且两球的数字和为3即抽到的是蓝2红1或者蓝1红2的概率,
则所求的概率为.
(2)解:“第一次取到的是红球”的概率,
“第二次取到了标记数字1的球”即取到的是数字2,1或者1,1,概率,
“第一次取到红球且第二次取到了标记数字1的球”即抽到的为红1数字1或者红2数字1,概率.
因为成立,所以事件与事件相互独立.
【解析】【分析】(1)第一类:求第一次取到的是红球,第二次取到的是蓝球且两球的数字和为3,即抽到红1蓝2或者红2蓝1的概率;第二类: 求第一次取到的是蓝球,第二次取到的是红球且两球的数字和为3即抽到的是蓝2红1或者蓝1红2的概率 ,然后概率相加即可;
(2) 求出事件、事件与事件的概率,验证与是否相等判断事件与事件是否相互独立.
5.【答案】(1)解:分别记第次摸到白球和黄球为事件,事件相互独立,
记“4次摸球后,袋子中球的颜色只有一种”为事件,
则;
(2)解:记“袋子中白球的个数为4”为事件.
,
故袋子中白球个数为4的概率为.
【解析】【分析】(1)记“4次摸球后,袋子中球的颜色只有一种”为事件D,由概率的乘法公式可得,进而计算可得答案;
(2)记“袋子中白球的个数为4”为事件,将满足条件的四种情况的概率求出,再用概率的加法进而计算可得答案.
6.【答案】(1)解:从第二个箱子取出黄球的概率,
从第三个箱子取出黄球的概率
(2)解:由题意可知,,
即,又,
.
【解析】【分析】(1)分第一次取出黄球和绿球两种情况,再由互斥事件概率加法公式计算;
(2)由题意可得,进而求解.
7.【答案】(1)解:设事件:甲投篮命中;事件:乙投篮命中;事件:丙投篮命中,
,,
甲、乙、丙各投篮一次,则甲和乙命中,丙不命中的概率为
.
所以甲、乙、丙各投篮一次,甲和乙命中,丙不命中的概率为0.21
(2)解:设事件:恰有一人命中.
所以
.
所以甲、乙、丙各投篮一次,恰有一人命中的概率为0.29
(3)解:设事件:至少有一人命中.
所以.
所以甲、乙、丙各投篮一次,至少有一人命中的概率为0.94
【解析】【分析】(1)根据概率乘法公式及对立事件的概率公式即可求解.
(2)根据相互独立事件的概率乘法公式及概率加法公式即可求解.
(3)利用正难则反易的思想,用对立事件的概率公式即可求解.
8.【答案】(1)解:在A类的4个问题中,甲每个问题答对的概率为,
所以甲在第一轮得最高分(即60分)的概率为,
在A类的4个问题中,乙只能答对3个问题,
设这4个问题分别为a,b,c,d,乙只会回答其中的a,b,c,
从中随机选三个问题所得的4个样本点为:a,b,c;a,b,d;a,c,d;b,c,d,
得60分的一个样本点为a,b,c,所以乙在第一轮得最高分(即60分)的概率为.
(2)解:甲在第一轮的得分可能为0,20,40,60,乙在第一轮的得分可能为40,60.
把甲在第一轮选择的3个问题分别记为e,f,g,答对分别记为E,F,G,
所以甲在第一轮得40分的概率为
,
甲在第一轮得60分的概率为,
甲在第二轮得分分类如下:
选10分和20分的题所得分数为10分和30分,
选10分和30分的题所得分数为10分和40分,
选20分和30分的题所得分数为0分、20分、30分和50分,
所以甲两轮的总积分不低于90分的概率为
.
由(1)得,乙在第一轮得40分的概率为,乙在第一轮得60分的概率为,
乙在第二轮得分分类如下:
选10分和20分的题所得分数为0分、10分、20分和30分,
选10分和30分的题所得分数为0分、10分、30分和40分,
选20分和30分的题所得分数为0分、20分、30分和50分,
所以乙两轮的总积分不低于90分的概率为
.
因为,所以乙晋级复赛的概率更大.
【解析】【分析】(1)根据相互独立事件求甲在第一轮得最高分的概率,利用古典概型求得乙在第一轮得最高分的概率;
(2)根据互斥事件和对立事件分别计算出甲和乙晋级复赛的概率,进而分析判断.
9.【答案】(1)解:依题意,设事件 “小张两轮都答对问题”, “小李两轮都答对问题”,
所以,.因为事件相互独立,
所以两人在两轮活动中都答对的概率为
(2)解:设事 “甲第一轮答对”, “乙第一轮答对”, “甲第二轮答对”, “乙第二轮答对”, “两人在两轮活动中至少答对3道题”,
则,
由事件的独立性与互斥性,可得
,
故两人在两轮活动中至少答对3道题的概率为.
(3)解:设事件,分别表示甲三轮答对2个,3个题目,,分别表示乙三轮答对2个,3个题目,
则,,,,
设事件 “两人在三轮活动中,小张和小李各自答对题目的个数相等且至少为2”,
则,且,,,分别相互独立,
所以.
所以两人在三轮活动中,小张和小李各自答对题目的个数相等且至少为2的概率为.
【解析】【分析】(1)根据题意结合独立事件概率乘法公式运算求解;
(2)两人分别答两次,总共四次中至少答对3道题,分五种情况,根据题意利用事件的独立性与互斥性分析运算;
(3)分小张和小李均答对两个题目、均答对三个题目两种情况,利用独立事件运算求解.
10.【答案】(1)解:设乙获得购物券的概率,
顾客乙答对每道题目的概率为,则答错每道题目的概率为,若无放回的抽取,则乙获得购物券的概率
(2)解:设丙第二次获得购物券的概率,
若有放回的抽取,顾客丙第二次抽到相同题目的概率为,
则顾客丙第二次抽到不同题目的概率为,
所以求丙第二次获得购物券的概率.
【解析】【分析】(1)乙获得购物券有第一次答对和第一次答错第二次答对两种情况 ,根据独立事件的概率公式;
(2)丙第二次获得购物券,则第一次必然答错,第二次答对有第二次抽到相同题目和第二次抽到不同题目答对两种情况,分别求解概率相加即可.
11.【答案】(1)解:设,分别表示甲、乙在第k(,2,3,…)轮射中,
则,.
设C表示“少年队”在一轮比赛中恰好射中1次,
则
,
所以“少年队”在一轮比赛中恰好射中1次的概率为.
(2)解:设,,,分别表示甲在三轮比赛中射中0次,1次,2次,3次,
,,,分别表示乙在三轮比赛中射中0次,1次,2次,3次,
M表示“少年队”在三轮比赛中恰好射中3次.
,,
,,
,,
,,
所以
,
故“少年队”在三轮比赛中恰好射中3次的概率为.
【解析】【分析】 (1)根据独立事件乘法公式和互斥事件加法公式进行计算,即可求出恰好射中1次的概率;
(2)根据二项分布算出甲和乙在三轮比赛中,射中0次,1次,2次,3次的概率,然后利用独立事件的乘法公式和互斥事件加法公式,即可求出恰好射中3次的概率.
12.【答案】(1)解:由独立事件的概率可知,四个开关均断开的概率为.
(2)解:、所在串联电路为通路的概率为,
、所在并联电路为通路的概率为,
若电路为通路,则两条线路至少有一个是通路的,
所以,电路为通路的概率为.
【解析】【分析】 (1) 由独立事件的概率乘法公式运算求解;
(2) 分别求串联、并联电路为通路的概率,再结合对立事件运算求解.
13.【答案】(1)解:设“一年内需要维修次”,,事件两两互斥,
因为一年内需要维修1次的占15%,维修2次的占6%,维修3次的占4%,
所以,
,
,
(2)解:这2台计算机保修期内维修次数总和不超过2次,则两台均未维修或1台维修0次另1台维修1次,或1台维修0次另1台维修2次,或2台各维修1次,
所以,这2台计算机保修期内维修次数总和不超过2次的概率为
.
【解析】【分析】(1)设“一年内需要维修次”,,根据题意结合互斥事件概率加法公式运算求解;
(2)这2台计算机保修期内维修次数总和不超过2次,则两台均未维修或1台维修0次另1台维修1次,或1台维修0次另1台维修2次,或2台各维修1次, 结合独立事件概率乘法公式运算求解.
14.【答案】(1)解:设“甲第轮猜对”为事件,“乙第轮猜对”为事件,
则,
记“经过两轮活动,两人共猜对2个成语”为事件C,
则事件有三种可能:甲全对、甲乙各对一个、乙全对,
所以.
(2)解:记“经过两轮活动,两人猜对成语的个数不相同”为事件D,
则事件有三种可能:均全错、均错一个、均全对,
所以,
所以
【解析】【分析】 (1) 由题意可知:共猜对2个成语有甲全对、甲乙各对一个、乙全对,结合独立事件概率乘法公式运算求解;
(2) 事件有三种可能:均全错、均错一个、均全对,结合独立事件概率乘法公式以及对立事件概率运算求解.
15.【答案】(1)解:由题意可得,
解得;
(2)解:因为总体共60名学生,样本容量为20,因此抽样比为.
其中分数段有人,分数段有人,
所以在分数段中抽取人,分数段抽取人,
设甲被抽到的事件为,乙被抽到的事件为,
则,,
则甲乙至少一人被抽到的概率为.
【解析】【分析】 (1) 根据频率和为1运算求解;
(2) 先根据分层抽样求各层人数,进而可得甲、乙被抽到的概率,结合独立事件概率乘法公式运算求解.
16.【答案】(1)解:记“甲家庭回答正确这道题”“乙家庭回答正确这道题”“丙家庭回答正确这道题”分别为事件A,B,C,
则,,,
即,,
所以,.
所以乙、丙两个家庭各自回答正确这道题的概率为和.
(2)解:有0个家庭回答正确的概率
,
有1个家庭回答正确的概率
,
所以不少于2个家庭回答正确这道题的概率.
【解析】【分析】本题考查相互独立事件的概率公式的运用,
(1)记“甲家庭回答正确这道题”“乙家庭回答正确这道题”“丙家庭回答正确这道题”分别为事件A,B,C,结合题意根据独立事件概率的公式即可得出乙、丙两个家庭各自回答正确这道题的概率为和;
(2)可以使用间接法求解,除去0个家庭和1个家庭回答正确的概率,剩下的概率就是不少于2个家庭回答正确这道题的概率,根据独立事件概率的求法分别求出有0个、1个家庭回答正确的概率分别为、,那么不少于2个家庭回答正确这道题的概率为.
17.【答案】(1)解:由,解得.
则这条鱼汞含量的样本平均数为.
(2)解:样本中汞含量在内的频率为.
则估计进口的这批鱼中共有条鱼汞含量超标.
(3)解:由题意可知,样本中汞含量在内的频率为,
则顾客甲购买的鱼汞含量有超标的概率为,
顾客乙购买的鱼汞含量有超标的概率为,
则恰有一人购买的鱼汞含量有超标的概率为.
【解析】【分析】(1)由频率之和等于1得出a,进而由平均数的公式求解即可;
(2)求出样本中汞含量在内的频率,利用频率进行估计;
(3)由概率的乘法公式计算甲乙两人购买的鱼汞含量有超标的概率,进而得出所求概率.
18.【答案】(1)解:由已知条件可得,每组的纵坐标的和乘以组距为1,所以,解得.
(2)解:由(1)知,所以调查评分在的人数占调查评分在人数的,若按分层抽样抽取3人,则调查评分在有1人,有2人,因为经过心理疏导后的恢复情况相互独立,所以选出的3人经过心理疏导后,心理等级均达不到良好的概率为,所以经过心理疏导后,至少有一人心理等级转为良好的概率为.
(3)解:由频率分布直方图可得,,估计市民心理健康问卷调查的平均评分为80.7,所以市民心理健康指数平均值为,
所以只需发放心理指导材料,不需要举办心理健康大讲堂活动.
【解析】【分析】(1)结合频率分布直方图性质及调查评分在的市民为400人计算n,t;
(2)利用分层抽样原理计算调查评分在和的人数,结合对立事件计算至少有一人心理等级转为“良好”的概率;
(3)利用频率分布直方图计算市民心理健康问卷调查的平均评分进而得到市民心理健康指数平均值判断该市是否需要举办心理健康大讲堂。
19.【答案】(1)解:令事件在一定时期内能研制出疫苗,事件在一定时期内能研制出疫苗,
事件在一定时期内能研制出疫苗,
由题意可知,事件、、相互独立,且,,.
若他们都研制出疫苗,即事件、、同时发生,
所以,,即他们都研制出疫苗的概率为.
(2)解:他们都失败,即事件、、同时发生,
所以,.
即他们都失败的概率为.
(3)解:“他们能够研制出疫苗”的对立事件为“他们都失败”,
结合对立事件间的概率关系,可得所求事件的概率.
即他们能研制出疫苗的概率为.
【解析】【分析】(1)利用相互独立事件同时发生的概率公式即可求解.
(2)先利用对立事件概率间的关系分别求出各自失败的概率,再利用相互独立事件同时发生的概率公式即可求解.
(3)先确定“他们能够研制出疫苗”的对立事件为“他们都失败”,再利用对立事件间的概率关系即可求解.
20.【答案】(1)解:由对餐厅评分的频率分布直方图,
得对餐厅“满意度指数”为4的频率为,
所以,对餐厅评价“满意度指数”为4的人数为(人).
(2)解:设“对餐厅评价‘满意度指数’比对餐厅评价‘满意度指数’低”为事件.
记“对餐厅评价‘满意度指数’为3”为事件;“对餐厅评价‘满意度指数’为4”为事件;
“对餐厅评价‘满意度指数’为4”为事件;“对餐厅评价‘满意度指数’'为5”为事件.
所以,,
由频率估计概率得:,.
因为事件与事件,事件与事件,事件与事件都相互对立,
所以
,
所以该学生对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率为0.32.
(3)解:设对餐厅“满意度指数”为,对餐厅“满意度指数”为,则
随机变量的取值有,
,
所以对餐厅“满意度指数”的分布列为:
3 4 5
0.2 0.4 0.4
随机变量的取值有,
,
所以餐厅“满意度指数”的分布列为:
3 4 5
0.1 0.55 0.35
所以,,
因为,
所以如果从学生对,两家餐厅评价的“满意度指数”的期望角度看,会选择餐厅用餐.
【解析】【分析】(1)根据频率分布直方图的性质可得结果.
(2)由相互独立事件和互斥事件的概率求和即可.
(3)分布求出对餐厅和B餐厅“满意度指数”的期望,通过比较期望大小可得结论.
21.【答案】(1)解:记选出的同学中至少有一个男同学为事件A,则;
(2)解:甲、乙被选中且通过测验的概率.
【解析】【分析】 (1)由题意知满足条件的事件是选出的3位同学中至少有一位男同学,它的对立事件是选出的3位同学中没有男同学,根据对立事件的概率公式得到至少有一个男同学的概率;
(2)由题意知10位同学中的女同学甲和男同学乙同时被选中表示再从另外的八人中选一人,根据相互独立事件的概率公式计算即可.
22.【答案】(1)解:A旅行社240人次的消费总额为元,
B旅行社240人次的消费总额为元,
因为,
所以B旅行社240人次的消费总额更大.
(2)解:对于A旅行社,这240人次去漓江的频率为,
所以甲去漓江的概率为.
对于B旅行社,这240人次去漓江的频率为,
所以乙去漓江的概率为.
故甲、乙至少有一人去漓江的概率为.
【解析】【分析】(1)根据柱状图分别计算旅行社A、B的消费总额,比较大小即可;
(2)根据频率计算出甲去漓江的概率为, 乙去漓江的概率为,再由对立事件的乘法公式计算即可得解.
23.【答案】(1)解:由题意可得:预定一张开幕式门票不成功的概率,成功的概率为,
设甲获得的门票数为,则的可能取值为,
故,
故的分布列为:
0 1 2
设乙获得的门票数为,则,
故,
故的分布列为:
0 1 2
故甲乙两人都没有获得任何门票的概率.
(2)解:由(1)可得:乙获得的门票数比甲多的概率.
【解析】【分析】(1) 由题意结合独立事件乘法求概率公式和对立事件求概率公式可得预定一张开幕式门票不成功的概率,再结合独立事件乘法求概率公式和对立事件求概率公式、互斥事件加法求概率公式得出成功的概率,设甲获得的门票数为,进而得出的可能取值,再利用独立事件乘法求概率公式和对立事件求概率公式、互斥事件加法求概率公式求出随机变量X的分布列,设乙获得的门票数为,则,再结合二项分布求概率公式得出随机变量Y的分布列,再利用独立事件乘法求概率公式得出甲乙两人都没有获得任何门票的概率。
(2) 由(1)结合独立事件乘法求概率公式和互斥事件加法求概率公式,从而得出乙获得的门票数比甲多的概率。
24.【答案】(1)解:线上同学平均分分;
线下同学平均分分;
又200名同学,线上人数占40%,线下人数占60%,
所以所有200名同学的平均分分.
(2)解:线上同学成绩良好人数为人,
线下同学成绩良好人数为人,
所以抽取数学成绩为良好,且,故线下的可能性大.
(3)解:由线下成绩中等同学人数为人,其它同学人,
所以从线下学生中随机抽取10名同学,抽到k个学生的成绩为中等的概率,且,
要使最大,则,即,
所以,则,故.
【解析】【分析】(1)利用已知条件结合频率分布直方图求平均数公式得出这200名学生的数学平均分。
(2)利用已知条件结合频率分布直方图中各小组的矩形的面积等于各小组的频率,再结合比较法判断出线下的可能性大。
(3) 利用已知条件结合频率分布直方图中各小组的频率等于各小组的矩形的面积,再结合频数等于频率乘以样本容量的公式得出线下成绩中等同学人数,进而得出其它同学人数,所以从线下学生中随机抽取10名同学,进而得出抽到k个学生的成绩为中等的概率,且,要使最大,则,进而得出实数k的取值范围,从而得出满足要求的k的值。
25.【答案】(1)解:设:第次通过第一关,:第次通过第二关,甲可以进入第三关的概率为,
由题意知
.
(2)解:设此次闯关活动的分数记为.
①由题意可知,
因为,且,
所以,则;
而,且,
所以前名参赛者的最低得分高于,
而甲的得分为分,所以甲能够获得奖励;
②假设乙所说为真,则,
,
而,所以,
从而,
而,
所以为小概率事件,即丙的分数为430分是小概率事件,可认为其不可能发生,但却又发生了,所以可认为乙所说为假.
【解析】【分析】(1) 设:第次通过第一关,:第次通过第二关, 计算 即可求出甲可以进入第三关的概率;
(2)①由 ,且 ,计算σ ,求出前400名参赛者的最低得分,与甲的得分比较即可;
②假设乙所说为真,由μ=201计算σ ,求出μ+3σ的值与430比较,即可得出结论.
26.【答案】(1)解:记事件A:直径约的结节在1年内发展为恶性肿瘤,事件B:该项无创血液检测的检查结果为阴性,
由题,,,,,,,则
所以患者甲检查结果为阴性的概率为0.8486.
(2)解:,
.
所以患者甲的检查结果为阴性,他的这个结节在1年内发展为恶性肿瘤的概率为0.00035.
(3)解:记参加该项检查的1000位患者中,获得20万元赔付的有X人,
,则,
记保险公司每年在这个项目上的收益为Y元,
,
则,
所以保险公司每年在这个项目上的收益估计为13万元.
【解析】【分析】(1) 利用已知条件结合条件概型求概率公式得出他的这个结节在1年内发展为恶性肿瘤的概率。
(2)利用已知条件结合随机变量X服从二项分布,再结合二项分布求数学期望公式得出X的数学期望, 记保险公司每年在这个项目上的收益为Y元 ,再利用数学期望的性质得出随机变量Y的数学期望。
27.【答案】(1)解:由题意得,击中靶心的频率与0.9接近,故概率约为0.9
(2)解:击中靶心的次数大约为 .
(3)解:由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定击不中靶心.
(4)解:由概率的意义知,不一定.
【解析】【分析】(1)由题意得,击中靶心的频率与0.9接近,再结合频率和概率的关系,从而得出该射击运动员射击一次,击中靶心的概率的值。
(2)利用已知条件结合频数等于频率乘以样本容量的公式,进而得出击中靶心的次数。
(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定击不中靶心。
(4)由概率的意义知第10次不一定击中靶心。
28.【答案】(1)解:记甲袋中红球是r,白球分别为 ,
由题意得顾客A可以从甲袋中先后摸出2个球,其所有等可能出现的结果为:
(r,r),(r, ),(r, ),( ,r),( , ),( , ),( ,r),( , ),( , )共9种,
其中结果(r, ),(r, ),( ,r),( ,r)可获奖金15元,
所以顾客A所获奖金为15元的概率为 .
(2)解:由题意的顾客A可以根据方案a抽奖两次或根据方案a,b各抽奖一次.
由(1)知顾客A根据方案a抽奖两次所获奖金及其概率如下表:
所获奖金(元) 0 15 30
概率
记乙袋中红球分别是R1,R2,白球W
则顾客A根据方案a,b各抽奖一次的所有等可能出现的结果为:
(r,R1),(r,R2),(r,W),( ,R1),( ,R2),( ,W),( ,R1),( ,R2),( ,W)共9种
其中结果(r,R1),(r,R2)可获奖金25元.结果(r,W)可获奖金15元,
( ,R1),( ,R2),( ,W),( ,R1),( ,R2)可获奖金10元,其余可获奖金0元,
所以顾客A根据方案a,b各抽奖一次所获奖金及其概率如下表:
所获奖金(元) 0 10 15 25
概率
由此可知顾客A最有可能获得的奖金数为15元.
【解析】【分析】(1)利用已知条件结合古典概型求概率公式得出其所获奖金为15元的概率。
(2) 利用已知条件结合列举法得出顾客A根据方案a,b各抽奖一次的所有等可能出现的结果,再利用古典概型求概率公式得出顾客A根据方案a,b各抽奖一次所获奖金及其概率,进而得出顾客A最有可能获得的奖金数。
29.【答案】(1)解:记A1表示事件“第2局结果为甲胜”,
A2表示事件“第3局甲参加比赛时,结果为甲负”,
A表示事件“第4局甲当裁判”.
则A=A1·A2.
.
(2)解:记表示事件“第1局结果为乙胜”,
表示事件“第2局乙参加比赛时,结果为乙胜”,
表示事件“第3局乙参加比赛时,结果为乙胜”,
B表示事件“前4局中恰好当1次裁判”.
则.
.
【解析】【分析】(1)设表示事件“第二局结果为甲胜”,表示事件“第三局甲参加比赛结果为负”,A表示事件“甲当裁判”,可得,利用相互独立事件的概率计算公式,即可求解.
(2)记表示事件“第1局结果为乙胜”,表示事件“第2局乙参加比赛时,结果为乙胜”,表示事件“第3局乙参加比赛时,结果为乙胜”,B表示事件“前4局中恰好当1次裁判”,利用相互独立事件的概率公式和互斥事件的概率加法公式,即可求解.
30.【答案】(1)解:设事件“甲第一轮猜对” ,事件“乙第一轮猜对” ,事件C=“甲第二轮猜对” ,事件“乙第二轮猜对 ,
甲、乙两人在两轮竞答活动中答对3题的概率为
解得或(舍去)
;
(2)解:三轮竞答活动中甲乙一共答6题,甲、乙两人在三轮竞答活动中答对4题,即总共有2题没有答对,
可能甲有两题没有答对,可能乙有两题没有答对,可能甲乙各有一题没有答对.
甲、乙两人在三轮竞答活动中答对4题的概率
【解析】【分析】(1)利用已知条件结合独立事件乘法求概率公式、对立事件求概率公式、互斥事件加法求概率公式,进而得出p的值。
(2) 利用已知条件结合二项分布求概率公式和互斥事件加法求概率公式,进而得出甲、乙两人在三轮竞答活动中答对4题的概率。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 概率综合卷 解答题专项
一、解答题
1.投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏.假设甲、乙、丙、丁是四位投壶游戏参与者,且甲、乙、丙每次投壶时,投中与不投中的机会是均等的,丁每次投壶时,投中的概率为.甲、乙、丙、丁每人每次投壶是否投中相互独立,互不影响.
(1)若甲、乙、丙、丁每人各投壶1次,求只有一人投中的概率;
(2)甲、丁进行投壶比赛,若甲、丁每人各投壶2次,投中次数多者获胜,求丁获胜的概率.
2.甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为,甲、乙都闯关成功的频率为,乙、丙都闯关成功的概率为,每人闯关成功记2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
3.(2023高三上·吉林开学考)甲乙两所友好学校举行篮球联谊赛,先获得3场比赛胜利的学校获得冠军并终止比赛,比赛交替在甲校与乙校进行,第一场比赛在甲校进行.已知甲队在主场(甲校)获胜的概率为,在客场(乙校)获胜的概率为,每场比赛要分出胜负且胜负概率不变.
(1)求甲队以3胜1负的成绩赢得冠军的概率;
(2)设篮球联谊赛比赛进行的场数为X,求随机变量X的分布列与期望.
4.(2023高一下·楚雄期末)袋中装有大小完全相同的6个红球,3个蓝球,其中有2个红球和1个蓝球上面标记了数字1,其他球标记了数字2.
(1)每次有放回地任取1个小球,连续取两次,求取出的2个球恰有1个红球且两球的数字和为3的概率;
(2)从袋中不放回地依次取2个小球,每次取1个,记事件第一次取到的是红球,事件第二次取到了标记数字1的球,求,并判断事件与事件是否相互独立.
5.已知1个不秀明的袋子中装有6个白球和4个黄球(这些球除颜色外无其他差异).甲从袋中摸出1球,若摸出的是白球,则除将摸出的白球放回袋子中外,再将袋子中的1个黄球拿出,放入1个白球;若摸出的是黄球,则除将摸出的黄球放回袋子中外,再将袋子中的1个白球拿出,放人1个黄球.再充分搅拌均匀后,进行第二次摸球,依此类推,直到袋中全部是同一种颜色的球,已知甲进行了4次摸球.
(1)求袋子中球的颜色只有一种的概率;
(2)求袋子中白球个数为4的概率.
6.(2024高三上·硚口)有编号为1,2,3,...,18,19,20的20个箱子,第一个箱子有2个黄球1个绿球,其余箱子均为2个黄球2个绿球,现从第一个箱子中取出一个球放入第二个箱子,再从第二个箱子中取出一个球放入第三个箱子,以此类推,最后从第19个箱子取出一个球放入第20个箱子,记为从第个箱子中取出黄球的概率.
(1)求;
(2)求.
7.(2023高一下·苏州期末)已知甲的投篮命中率为0.6,乙的投篮命中率为0.7,丙的投篮命中率为0.5.
(1)甲、乙、丙各投篮一次,求甲和乙命中,丙不命中的概率;
(2)甲、乙、丙各投篮一次,求恰有一人命中的概率;
(3)甲、乙、丙各投篮一次,求至少有一人命中的概率.
8.(2023高一下·湖南期末)某学校组织人工智能知识竞赛,在初赛中有两轮答题,第一轮从A类的4个问题中随机抽取3题作答,每答对1题得20分,答错得0分;第二轮从B类分值分别为10,20,30的3个问题中随机抽取2题作答,每答对1题该题得满分,答错得0分.若两轮总积分不低于90分则晋级复赛.甲、乙同时参赛,在A类的4个问题中,甲每个问题答对的概率为,乙只能答对3个问题;在B类3个分值分别为10,20,30的问题中,甲答对的概率分别为1,,,乙答对的概率分别为,,.甲、乙回答任一问题正确与否互不影响.
(1)分别求甲、乙在第一轮得最高分的概率;
(2)谁晋级复赛的概率更大?请说明理由.
9.(2023高一下·河南月考)大学毕业生小张和小李通过了某单位的招聘笔试考试,正在积极准备结构化面试,每天相互进行多轮测试,每轮由小张和小李各回答一个问题,已知小张每轮答对的概率为,小李每轮答对的概率为.在每轮活动中,小张和小李答对与否互不影响,各轮结果也互不影响.
(1)求两人在两轮活动中都答对的概率;
(2)求两人在两轮活动中至少答对3道题的概率;
(3)求两人在三轮活动中,小张和小李各自答对题目的个数相等且至少为2的概率.
10.(2023高一下·达州期末)某超市将若干个问题印在质地、大小相同的小球上,顾客每次随机抽出个小球并回答上面的问题.若顾客第一次答对,则获得购物券并结束活动:若顾客第一次答错,就再抽一次,答对获得购物券并结束活动,答错结束活动.顾客对不同题目的回答是独立的.
(1)顾客乙答对每道题目的概率为,若无放回的抽取,求乙获得购物券的概率:
(2)顾客丙首次答对每道题目的概率为,对相同题目答对的概率为.若有放回的抽取,顾客丙第二次抽到相同题目的概率为,求丙第二次获得购物券的概率.
11.(2023高一下·莲湖期末)某学校派甲、乙两人组成“少年队”参加射击比赛,每轮比赛由甲、乙各射击一次,已知甲每轮射中的概率为,乙每轮射中的概率为.在每轮比赛中,甲和乙射中与否互不影响,各轮比赛结果也互不影响.
(1)求“少年队”在一轮比赛中恰好射中1次的概率;
(2)求“少年队”在三轮比赛中恰好射中3次的概率.
12.(2023高一下·海南期末)在如图所示的电路中,、、、四个开关闭合的概率分别为、、、,且各个开关是否闭合是相互独立的.
(1)求四个开关均断开的概率;
(2)求电路为通路的概率
13.(2023高一下·荔湾期末)某品牌计算机售后保修期为1年,根据大量的维修记录资料,这种品牌的计算机在使用一年内维修次数最多的是3次,其中维修1次的占15%,维修2次的占6%,维修3次的占4%.
(1)若某人购买1台这种品牌的计算机,求下列事件的概率:A=“在保修期内需要维修”;B=“在保修期内维修不超过1次”;
(2)若某人购买2台这种品牌的计算机,2台计算机在保修期内是否需要维修互不影响,求这2台计算机保修期内维修次数总和不超过2次的概率.
14.(2023高一下·广州期末)甲、乙两人参加猜成语活动,每轮活动由甲、乙各猜一个成语,已知甲每轮猜对的概率为,乙每轮猜对的概率为.在每轮活动中,甲和乙猜对与否互不影响,各轮结果也互不影响.
(1)求经过两轮活动,两人共猜对2个成语的概率;
(2)求经过两轮活动,两人猜对成语的个数不相同的概率.
15.(2023高二下·嘉定期末)某校高二年级一个班有60名学生,将期中考试的数学成绩(均为整数)分成六段:,得到如图所示的频率分布直方图,
(1)求的值;
(2)用分层随机抽样的方法从中抽取一个容量为20的样本,已知甲同学的成绩在,乙同学的成绩在,求甲乙至少一人被抽到的概率.
16.(2023高一下·余姚期末)为了纪念2017年在德国波恩举行的联合国气候大会,某社区举办《“环保我参与”有奖问答比赛》活动.某场比赛中,甲、乙、丙三个家庭同时回答一道有关环保知识的问题.已知甲家庭回答正确这道题的概率是,甲、丙两个家庭都回答错误的概率是,乙、丙两个家庭都回答正确的概率是.若各家庭回答是否正确互不影响.
(1)求乙、丙两个家庭各自回答正确这道题的概率;
(2)求甲、乙、丙三个家庭中不少于2个家庭回答正确这道题的概率.
17.(2023高一下·温州期末) 现行国家标准中规定了10大类食品中重金属汞的污染限量值,其中肉食性鱼类及其制品中汞的最大残留量为,近日某水产市场进口了一批冰鲜鱼2000条,从中随机抽取了200条鱼作为样本,检测鱼体汞含量与其体重的比值,由测量结果制成如图所示的频率分布直方图.
(1)求的值,并估计这200条鱼汞含量的样本平均数;
(2)用样本估计总体的思想,估计进口的这批鱼中共有多少条鱼汞含量超标;
(3)从这批鱼中顾客甲购买了2条,顾客乙购买了1条,甲乙互不影响,求恰有一人购买的鱼汞含量有超标的概率.
18.(2023高一下·湖州期末)习近平总书记指出:“要健全社会心理服务体系和疏导机制、危机干预机制,塑造自尊自信、理性平和、亲善友爱的社会心态.”在2022年新冠肺炎疫情防控阻击战中,心理医生的相关心理疏导起到了重要作用.某心理调查机构为了解市民在疫情期间的心理健康状况,随机抽取n位市民进行心理健康问卷调查,按所得评分(满分100分)从低到高将心理健康状况分为四个等级:
调查评分
心理等级 有隐患 一般 良好 优秀
并绘制如图所示的频率分布直方图.已知调查评分在的市民为400人.
(1)求n的值及频率分布直方图中t的值;
(2)在抽取的心理等级为“有隐患”的市民中,按照调查评分分层抽取3人进行心理疏导.据以往数据统计,经过心理疏导后,调查评分在的市民心理等级转为“良好”的概率为,调查评分在的市民心理等级转为“良好”的概率为,若经过心理疏导后的恢复情况相互独立,试问在抽取的3人中,经过心理疏导后,至少有一人心理等级转为“良好”的概率为多少?
(3)心理调查机构与该市管理部门设定的预案是:以抽取的样本作为参考,若市民心理健康指数平均值不低于0.8,则只需发放心理指导资料,否则需要举办心理健康大讲堂.根据你所学的统计知识,判断该市是否需要举办心理健康大讲堂,并说明理由.
注:每组数据以区间的中点值代替,心理健康指数=问卷调查评分/100.
19.(2023高三下·玉林模拟)年月日,中国疾控中心成功分离中国首株新型冠状病毒毒种,月日时分,重组新冠疫苗获批启动临床试验.月日,中国新冠病毒疫苗进入期临床试验截至月日,全球当前有大约种候选新冠病毒疫苗在研发中,其中至少有种疫苗正处于临床试验阶段现有、、三个独立的医疗科研机构,它们在一定时期内能研制出疫苗的概率分别是、、.求:
(1)他们都研制出疫苗的概率;
(2)他们都失败的概率;
(3)他们能够研制出疫苗的概率.
20.(2023高二下·普宁月考)某大学为调研学生在,两家餐厅用餐的满意度,从在,两家餐厅都用过餐的学生中各随机抽取了200人,每人分别对这两家餐厅进行评分,满分为60分.整理评分数据,将分数分成6组:,,,,,,得到餐厅分数的频率分布直方图和餐厅分数的频数分布表:
餐厅分数的频数分布表:
分数区间 频数
4
6
10
30
80
70
定义学生对餐厅评价的“满意度指数”如下:
分数
满意度指数 3 4 5
(1)在抽样的200人中,求对餐厅评价“满意度指数”为4的人数;
(2)从该校在,两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率;
(3)如果从,两家餐厅中选择一家用餐,从期望的角度你会选择哪一家?并说明理由.
21.(2023高二下·浙江期中)从10名同学(其中6女4男)中随机选出3人参加测验,每个女同学通过测验的概率均为,每个男同学通过测验的概率均为,求:
(1)选出的3个同学中,至少有一个男同学的概率;
(2)10个同学中的女同学甲和男同学乙同时被选中且通过测验的概率.
22.(2023·湛江模拟)现有A,B两个广西旅行社,统计了这两个旅行社的游客去漓江、乐满地主题乐园、西街、龙脊梯田四个景点旅游的各240人次的数据,并分别绘制出这两个旅行社240人次分布的柱形图,如图所示.假设去漓江、乐满地主题乐园、西街、龙脊梯田旅游每人次的平均消费分别为1200元、1000元、600元、200元.
(1)通过计算,比较这两个旅行社240人次的消费总额哪个更大;
(2)若甲和乙分别去A旅行社、B旅行社,并都从这四个景点中选择一个去旅游,以这240人次去漓江的频率为概率,求甲、乙至少有一人去漓江的概率.
23.(2023·株洲模拟)2023年亚运会在中国杭州举办,开幕式门票与其他赛事门票在网上开始预定,亚奥理事会规定:开幕式门票分为A、B两档,当预定A档未成功时,系统自动进入B档预定,已知获得A档门票的概率是,若未成功,仍有的概率获得B档门票的机会;而成功获得其他赛事门票的概率均为,且获得每张门票之间互不影响.甲预定了一张A档开幕式门票,一张赛事门票;乙预定了两张赛事门票.
(1)求甲乙两人都没有获得任何门票的概率;
(2)求乙获得的门票数比甲多的概率.
24.(2023·张家界模拟)2022年底,新冠病毒肆虐全国,很多高三同学也都加入羊羊行列.某校参加某次大型考试时采用了线上考试和线下考试两种形式.现随机抽取200名同学的数学成绩做分析,其中线上人数占40%,线下人数占60%,通过分别统计他们的数学成绩得到了如下两个频率分部直方图:
其中称为合格,称为中等,称为良好,称为优秀,称为优异.
(1)根据频率分布直方图,求这200名学生的数学平均分(同一组数据可取该组区间的中点值代替);
(2)现从这200名学生中随机抽取一名同学的数学成绩为良好,试分析他是来自线上考试的可能性大,还是来自线下考试的可能性大.
(3)现从线下考试的学生中随机抽取10名同学,且抽到k个学生的数学成绩为中等的可能性最大,试求k的值.
25.(2023·重庆市模拟)某网络在平台开展了一项有奖闯关活动,并对每一关根据难度进行赋分,竞猜活动共五关,规定:上一关不通过则不进入下一关,本关第一次未通过有再挑战一次的机会,两次均未通过,则闯关失败,且各关能否通过相互独立,已知甲、乙、丙三人都参加了该项活动.
附:若随机变量,则;;.
(1)若甲第一关通过的概率为,第二关通过的概率为,求甲可以进入第三关的概率;
(2)已知该闯关活动累计得分服从正态分布,且满分为450分,现要根据得分给共2500名参加者中得分前400名发放奖励,
①假设该闯关活动平均分数为171分,351分以上共有57人,已知甲的得分为270分,问甲能否获得奖励,请说明理由;
②丙得知他的分数为430分,而乙告诉丙:“这次闯关活动平均分数为201分,351分以上共有57人”,请结合统计学知识帮助丙辨别乙所说信息的真伪.
26.(2023·蚌埠模拟)有研究显示,人体内某部位的直径约的结节约有0.2%的可能性会在1年内发展为恶性肿瘤.某医院引进一台检测设备,可以通过无创的血液检测,估计患者体内直径约的结节是否会在1年内发展为恶性肿瘤,若检测结果为阳性,则提示该结节会在1年内发展为恶性肿瘤,若检测结果为阴性,则提示该结节不会在1年内发展为恶性肿瘤.这种检测的准确率为85%,即一个会在1年内发展为恶性肿瘤的患者有85%的可能性被检出阳性,一个不会在1年内发展为恶性肿瘤的患者有85%的可能性被检出阴性.患者甲被检查出体内长了一个直径约的结节,他做了该项无创血液检测.
(1)求患者甲检查结果为阴性的概率;
(2)若患者甲的检查结果为阴性,求他的这个结节在1年内发展为恶性肿瘤的概率(结果保留5位小数);
(3)医院为每位参加该项检查的患者缴纳200元保险费,对于检测结果为阴性,但在1年内发展为恶性肿瘤的患者,保险公司赔付该患者20万元,若每年参加该项检查的患者有1000人,请估计保险公司每年在这个项目上的收益.
27.某射击运动员为备战奥运会,在相同条件下进行射击训练,结果如下:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率 0.8 0.95 0.88 0.92 0.89 0.91
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗?
(4)假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?
28.某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖规则如下:1、抽奖方案有以下两种:方案,从装有1个红球、2个白球仅颜色不同的甲袋中随机摸出1个球,若是红球,则获得奖金15元,否则,没有奖金,兑奖后将摸出的球放回甲袋中;方案,从装有2个红、1个白球仅颜色不同的乙袋中随机摸出1个球,若是红球,则获得奖金10元,否则,没有奖金,兑奖后将摸出的球放回乙袋中.2.抽奖条件是:顾客购买商品的金额满100元,可根据方案抽奖一;满足150元,可根据方案抽奖例如某顾客购买商品的金额为310元,则该顾客采用的抽奖方式可以有以下三种,根据方案抽奖三次或方案抽奖两次或方案,各抽奖一次已知顾客在该商场购买商品的金额为250元.
(1)若顾客只选择根据方案进行抽奖,求其所获奖金为15元的概率;
(2)当若顾客采用每种抽奖方式的可能性都相等,求其最有可能获得的奖金数(0元除外.
29.(2023高二上·湖北月考)甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为各局比赛的结果都相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)求前4局中乙恰好当1次裁判概率.
30.(2023高二上·佛山期末)每年的11月9日是我国的全国消防日.119为我国规定的统一火灾报警电话,但119台不仅仅是一部电话,也是一套先进的通讯系统.它可以同中国国土上任何一个地方互通重大灾害情报,还可以通过卫星调集防灾救援力量,向消防最高指挥提供火情信息.佛山某中学为了加强学生的消防安全意识,防范安全风险,特在11月9日组织消防安全系列活动.甲、乙两人组队参加消防安全知识竞答活动,每轮竞答活动由甲、乙各答一题.在每轮竞答中,甲和乙答对与否互不影响,各轮结果也互不影响.已知甲每轮答对的概率为,乙每轮答对的概率为,且甲、乙两人在两轮竞答活动中答对3题的概率为.
(1)求的值;
(2)求甲、乙两人在三轮竞答活动中答对4题的概率.
答案解析部分
1.【答案】(1)解:设甲、乙、丙、丁各自在一次投壶中投中分别记为事件A,B,C,D,
则,.
设只有一人投中为事件E,则
.
(2)解:若甲投中0次,则丁至少投中1次;若甲投中1次,则丁投中2次.
设丁获胜为事件M,则.
【解析】【分析】(1) 设甲、乙、丙、丁各自在一次投壶中投中分别记为事件A,B,C,D,则,,然后根据独立事件乘法公式计算即可得解;
(2)分情况讨论,甲投中0次,则丁至少投中1次;若甲投中1次,则丁投中2次.根据独立重复事件公式计算即可得解.
2.【答案】(1)解:三人各自独立闯关,其中甲闯关成功的概率为,
甲、乙都闯关成功的概率为,乙、丙都闯关成功的概率为,
设乙闯关成功的概率为,丙闯关成功的概率为,
∵乙丙独立闯关,
根据独立事件同时发生的概率公式得:.
解得,.
即乙闯关成功的概率为,丙闯关成功的概率为.
(2)解:团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为4分”为事件A,
则,
即团体总分为4分的概率为.
(3)解:团体总分不小于4分,即团体总分为4分或6分,设“团体总分不小于4分”为事件B,
由(2)知团体总分为4分的概率为,
团体总分为6分,即3人都闯关成功的概率为.
所以参加复赛的概率为.
即该小组参加复赛的概率为.
【解析】【分析】 (1)设乙闯关成功的概率为,丙闯关成功的概率为, 结合独立事件概率乘法公式运算求解;
(2)由题意可知: 团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关,结合互斥事件概率和独立事件概率乘法公式运算求解;
(3) 若团体总分不小于4分,则团体总分为4分或6分,结合互斥事件概率和独立事件概率乘法公式运算求解.
3.【答案】(1)解:设事件A为:“甲队以3胜1负的成绩赢得冠军”,
则.
(2)解:由题意:X的可能取值为3,4,5.
则,,
,故随机变量X的分布列为:
X 3 4 5
P
则.
【解析】【分析】(1) 甲队以3胜1负的成绩赢得冠军 ,讨论甲队输球的可能场次,结合独立事件概率乘法公式运算求解;
(2)分析可知 X的可能取值为3,4,5,结合题意求分布列和期望.
4.【答案】(1)解:第一次取到的是红球,第二次取到的是蓝球且两球的数字和为3,即抽到红1蓝2或者红2蓝1的概率:,
第一次取到的是蓝球,第二次取到的是红球且两球的数字和为3即抽到的是蓝2红1或者蓝1红2的概率,
则所求的概率为.
(2)解:“第一次取到的是红球”的概率,
“第二次取到了标记数字1的球”即取到的是数字2,1或者1,1,概率,
“第一次取到红球且第二次取到了标记数字1的球”即抽到的为红1数字1或者红2数字1,概率.
因为成立,所以事件与事件相互独立.
【解析】【分析】(1)第一类:求第一次取到的是红球,第二次取到的是蓝球且两球的数字和为3,即抽到红1蓝2或者红2蓝1的概率;第二类: 求第一次取到的是蓝球,第二次取到的是红球且两球的数字和为3即抽到的是蓝2红1或者蓝1红2的概率 ,然后概率相加即可;
(2) 求出事件、事件与事件的概率,验证与是否相等判断事件与事件是否相互独立.
5.【答案】(1)解:分别记第次摸到白球和黄球为事件,事件相互独立,
记“4次摸球后,袋子中球的颜色只有一种”为事件,
则;
(2)解:记“袋子中白球的个数为4”为事件.
,
故袋子中白球个数为4的概率为.
【解析】【分析】(1)记“4次摸球后,袋子中球的颜色只有一种”为事件D,由概率的乘法公式可得,进而计算可得答案;
(2)记“袋子中白球的个数为4”为事件,将满足条件的四种情况的概率求出,再用概率的加法进而计算可得答案.
6.【答案】(1)解:从第二个箱子取出黄球的概率,
从第三个箱子取出黄球的概率
(2)解:由题意可知,,
即,又,
.
【解析】【分析】(1)分第一次取出黄球和绿球两种情况,再由互斥事件概率加法公式计算;
(2)由题意可得,进而求解.
7.【答案】(1)解:设事件:甲投篮命中;事件:乙投篮命中;事件:丙投篮命中,
,,
甲、乙、丙各投篮一次,则甲和乙命中,丙不命中的概率为
.
所以甲、乙、丙各投篮一次,甲和乙命中,丙不命中的概率为0.21
(2)解:设事件:恰有一人命中.
所以
.
所以甲、乙、丙各投篮一次,恰有一人命中的概率为0.29
(3)解:设事件:至少有一人命中.
所以.
所以甲、乙、丙各投篮一次,至少有一人命中的概率为0.94
【解析】【分析】(1)根据概率乘法公式及对立事件的概率公式即可求解.
(2)根据相互独立事件的概率乘法公式及概率加法公式即可求解.
(3)利用正难则反易的思想,用对立事件的概率公式即可求解.
8.【答案】(1)解:在A类的4个问题中,甲每个问题答对的概率为,
所以甲在第一轮得最高分(即60分)的概率为,
在A类的4个问题中,乙只能答对3个问题,
设这4个问题分别为a,b,c,d,乙只会回答其中的a,b,c,
从中随机选三个问题所得的4个样本点为:a,b,c;a,b,d;a,c,d;b,c,d,
得60分的一个样本点为a,b,c,所以乙在第一轮得最高分(即60分)的概率为.
(2)解:甲在第一轮的得分可能为0,20,40,60,乙在第一轮的得分可能为40,60.
把甲在第一轮选择的3个问题分别记为e,f,g,答对分别记为E,F,G,
所以甲在第一轮得40分的概率为
,
甲在第一轮得60分的概率为,
甲在第二轮得分分类如下:
选10分和20分的题所得分数为10分和30分,
选10分和30分的题所得分数为10分和40分,
选20分和30分的题所得分数为0分、20分、30分和50分,
所以甲两轮的总积分不低于90分的概率为
.
由(1)得,乙在第一轮得40分的概率为,乙在第一轮得60分的概率为,
乙在第二轮得分分类如下:
选10分和20分的题所得分数为0分、10分、20分和30分,
选10分和30分的题所得分数为0分、10分、30分和40分,
选20分和30分的题所得分数为0分、20分、30分和50分,
所以乙两轮的总积分不低于90分的概率为
.
因为,所以乙晋级复赛的概率更大.
【解析】【分析】(1)根据相互独立事件求甲在第一轮得最高分的概率,利用古典概型求得乙在第一轮得最高分的概率;
(2)根据互斥事件和对立事件分别计算出甲和乙晋级复赛的概率,进而分析判断.
9.【答案】(1)解:依题意,设事件 “小张两轮都答对问题”, “小李两轮都答对问题”,
所以,.因为事件相互独立,
所以两人在两轮活动中都答对的概率为
(2)解:设事 “甲第一轮答对”, “乙第一轮答对”, “甲第二轮答对”, “乙第二轮答对”, “两人在两轮活动中至少答对3道题”,
则,
由事件的独立性与互斥性,可得
,
故两人在两轮活动中至少答对3道题的概率为.
(3)解:设事件,分别表示甲三轮答对2个,3个题目,,分别表示乙三轮答对2个,3个题目,
则,,,,
设事件 “两人在三轮活动中,小张和小李各自答对题目的个数相等且至少为2”,
则,且,,,分别相互独立,
所以.
所以两人在三轮活动中,小张和小李各自答对题目的个数相等且至少为2的概率为.
【解析】【分析】(1)根据题意结合独立事件概率乘法公式运算求解;
(2)两人分别答两次,总共四次中至少答对3道题,分五种情况,根据题意利用事件的独立性与互斥性分析运算;
(3)分小张和小李均答对两个题目、均答对三个题目两种情况,利用独立事件运算求解.
10.【答案】(1)解:设乙获得购物券的概率,
顾客乙答对每道题目的概率为,则答错每道题目的概率为,若无放回的抽取,则乙获得购物券的概率
(2)解:设丙第二次获得购物券的概率,
若有放回的抽取,顾客丙第二次抽到相同题目的概率为,
则顾客丙第二次抽到不同题目的概率为,
所以求丙第二次获得购物券的概率.
【解析】【分析】(1)乙获得购物券有第一次答对和第一次答错第二次答对两种情况 ,根据独立事件的概率公式;
(2)丙第二次获得购物券,则第一次必然答错,第二次答对有第二次抽到相同题目和第二次抽到不同题目答对两种情况,分别求解概率相加即可.
11.【答案】(1)解:设,分别表示甲、乙在第k(,2,3,…)轮射中,
则,.
设C表示“少年队”在一轮比赛中恰好射中1次,
则
,
所以“少年队”在一轮比赛中恰好射中1次的概率为.
(2)解:设,,,分别表示甲在三轮比赛中射中0次,1次,2次,3次,
,,,分别表示乙在三轮比赛中射中0次,1次,2次,3次,
M表示“少年队”在三轮比赛中恰好射中3次.
,,
,,
,,
,,
所以
,
故“少年队”在三轮比赛中恰好射中3次的概率为.
【解析】【分析】 (1)根据独立事件乘法公式和互斥事件加法公式进行计算,即可求出恰好射中1次的概率;
(2)根据二项分布算出甲和乙在三轮比赛中,射中0次,1次,2次,3次的概率,然后利用独立事件的乘法公式和互斥事件加法公式,即可求出恰好射中3次的概率.
12.【答案】(1)解:由独立事件的概率可知,四个开关均断开的概率为.
(2)解:、所在串联电路为通路的概率为,
、所在并联电路为通路的概率为,
若电路为通路,则两条线路至少有一个是通路的,
所以,电路为通路的概率为.
【解析】【分析】 (1) 由独立事件的概率乘法公式运算求解;
(2) 分别求串联、并联电路为通路的概率,再结合对立事件运算求解.
13.【答案】(1)解:设“一年内需要维修次”,,事件两两互斥,
因为一年内需要维修1次的占15%,维修2次的占6%,维修3次的占4%,
所以,
,
,
(2)解:这2台计算机保修期内维修次数总和不超过2次,则两台均未维修或1台维修0次另1台维修1次,或1台维修0次另1台维修2次,或2台各维修1次,
所以,这2台计算机保修期内维修次数总和不超过2次的概率为
.
【解析】【分析】(1)设“一年内需要维修次”,,根据题意结合互斥事件概率加法公式运算求解;
(2)这2台计算机保修期内维修次数总和不超过2次,则两台均未维修或1台维修0次另1台维修1次,或1台维修0次另1台维修2次,或2台各维修1次, 结合独立事件概率乘法公式运算求解.
14.【答案】(1)解:设“甲第轮猜对”为事件,“乙第轮猜对”为事件,
则,
记“经过两轮活动,两人共猜对2个成语”为事件C,
则事件有三种可能:甲全对、甲乙各对一个、乙全对,
所以.
(2)解:记“经过两轮活动,两人猜对成语的个数不相同”为事件D,
则事件有三种可能:均全错、均错一个、均全对,
所以,
所以
【解析】【分析】 (1) 由题意可知:共猜对2个成语有甲全对、甲乙各对一个、乙全对,结合独立事件概率乘法公式运算求解;
(2) 事件有三种可能:均全错、均错一个、均全对,结合独立事件概率乘法公式以及对立事件概率运算求解.
15.【答案】(1)解:由题意可得,
解得;
(2)解:因为总体共60名学生,样本容量为20,因此抽样比为.
其中分数段有人,分数段有人,
所以在分数段中抽取人,分数段抽取人,
设甲被抽到的事件为,乙被抽到的事件为,
则,,
则甲乙至少一人被抽到的概率为.
【解析】【分析】 (1) 根据频率和为1运算求解;
(2) 先根据分层抽样求各层人数,进而可得甲、乙被抽到的概率,结合独立事件概率乘法公式运算求解.
16.【答案】(1)解:记“甲家庭回答正确这道题”“乙家庭回答正确这道题”“丙家庭回答正确这道题”分别为事件A,B,C,
则,,,
即,,
所以,.
所以乙、丙两个家庭各自回答正确这道题的概率为和.
(2)解:有0个家庭回答正确的概率
,
有1个家庭回答正确的概率
,
所以不少于2个家庭回答正确这道题的概率.
【解析】【分析】本题考查相互独立事件的概率公式的运用,
(1)记“甲家庭回答正确这道题”“乙家庭回答正确这道题”“丙家庭回答正确这道题”分别为事件A,B,C,结合题意根据独立事件概率的公式即可得出乙、丙两个家庭各自回答正确这道题的概率为和;
(2)可以使用间接法求解,除去0个家庭和1个家庭回答正确的概率,剩下的概率就是不少于2个家庭回答正确这道题的概率,根据独立事件概率的求法分别求出有0个、1个家庭回答正确的概率分别为、,那么不少于2个家庭回答正确这道题的概率为.
17.【答案】(1)解:由,解得.
则这条鱼汞含量的样本平均数为.
(2)解:样本中汞含量在内的频率为.
则估计进口的这批鱼中共有条鱼汞含量超标.
(3)解:由题意可知,样本中汞含量在内的频率为,
则顾客甲购买的鱼汞含量有超标的概率为,
顾客乙购买的鱼汞含量有超标的概率为,
则恰有一人购买的鱼汞含量有超标的概率为.
【解析】【分析】(1)由频率之和等于1得出a,进而由平均数的公式求解即可;
(2)求出样本中汞含量在内的频率,利用频率进行估计;
(3)由概率的乘法公式计算甲乙两人购买的鱼汞含量有超标的概率,进而得出所求概率.
18.【答案】(1)解:由已知条件可得,每组的纵坐标的和乘以组距为1,所以,解得.
(2)解:由(1)知,所以调查评分在的人数占调查评分在人数的,若按分层抽样抽取3人,则调查评分在有1人,有2人,因为经过心理疏导后的恢复情况相互独立,所以选出的3人经过心理疏导后,心理等级均达不到良好的概率为,所以经过心理疏导后,至少有一人心理等级转为良好的概率为.
(3)解:由频率分布直方图可得,,估计市民心理健康问卷调查的平均评分为80.7,所以市民心理健康指数平均值为,
所以只需发放心理指导材料,不需要举办心理健康大讲堂活动.
【解析】【分析】(1)结合频率分布直方图性质及调查评分在的市民为400人计算n,t;
(2)利用分层抽样原理计算调查评分在和的人数,结合对立事件计算至少有一人心理等级转为“良好”的概率;
(3)利用频率分布直方图计算市民心理健康问卷调查的平均评分进而得到市民心理健康指数平均值判断该市是否需要举办心理健康大讲堂。
19.【答案】(1)解:令事件在一定时期内能研制出疫苗,事件在一定时期内能研制出疫苗,
事件在一定时期内能研制出疫苗,
由题意可知,事件、、相互独立,且,,.
若他们都研制出疫苗,即事件、、同时发生,
所以,,即他们都研制出疫苗的概率为.
(2)解:他们都失败,即事件、、同时发生,
所以,.
即他们都失败的概率为.
(3)解:“他们能够研制出疫苗”的对立事件为“他们都失败”,
结合对立事件间的概率关系,可得所求事件的概率.
即他们能研制出疫苗的概率为.
【解析】【分析】(1)利用相互独立事件同时发生的概率公式即可求解.
(2)先利用对立事件概率间的关系分别求出各自失败的概率,再利用相互独立事件同时发生的概率公式即可求解.
(3)先确定“他们能够研制出疫苗”的对立事件为“他们都失败”,再利用对立事件间的概率关系即可求解.
20.【答案】(1)解:由对餐厅评分的频率分布直方图,
得对餐厅“满意度指数”为4的频率为,
所以,对餐厅评价“满意度指数”为4的人数为(人).
(2)解:设“对餐厅评价‘满意度指数’比对餐厅评价‘满意度指数’低”为事件.
记“对餐厅评价‘满意度指数’为3”为事件;“对餐厅评价‘满意度指数’为4”为事件;
“对餐厅评价‘满意度指数’为4”为事件;“对餐厅评价‘满意度指数’'为5”为事件.
所以,,
由频率估计概率得:,.
因为事件与事件,事件与事件,事件与事件都相互对立,
所以
,
所以该学生对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率为0.32.
(3)解:设对餐厅“满意度指数”为,对餐厅“满意度指数”为,则
随机变量的取值有,
,
所以对餐厅“满意度指数”的分布列为:
3 4 5
0.2 0.4 0.4
随机变量的取值有,
,
所以餐厅“满意度指数”的分布列为:
3 4 5
0.1 0.55 0.35
所以,,
因为,
所以如果从学生对,两家餐厅评价的“满意度指数”的期望角度看,会选择餐厅用餐.
【解析】【分析】(1)根据频率分布直方图的性质可得结果.
(2)由相互独立事件和互斥事件的概率求和即可.
(3)分布求出对餐厅和B餐厅“满意度指数”的期望,通过比较期望大小可得结论.
21.【答案】(1)解:记选出的同学中至少有一个男同学为事件A,则;
(2)解:甲、乙被选中且通过测验的概率.
【解析】【分析】 (1)由题意知满足条件的事件是选出的3位同学中至少有一位男同学,它的对立事件是选出的3位同学中没有男同学,根据对立事件的概率公式得到至少有一个男同学的概率;
(2)由题意知10位同学中的女同学甲和男同学乙同时被选中表示再从另外的八人中选一人,根据相互独立事件的概率公式计算即可.
22.【答案】(1)解:A旅行社240人次的消费总额为元,
B旅行社240人次的消费总额为元,
因为,
所以B旅行社240人次的消费总额更大.
(2)解:对于A旅行社,这240人次去漓江的频率为,
所以甲去漓江的概率为.
对于B旅行社,这240人次去漓江的频率为,
所以乙去漓江的概率为.
故甲、乙至少有一人去漓江的概率为.
【解析】【分析】(1)根据柱状图分别计算旅行社A、B的消费总额,比较大小即可;
(2)根据频率计算出甲去漓江的概率为, 乙去漓江的概率为,再由对立事件的乘法公式计算即可得解.
23.【答案】(1)解:由题意可得:预定一张开幕式门票不成功的概率,成功的概率为,
设甲获得的门票数为,则的可能取值为,
故,
故的分布列为:
0 1 2
设乙获得的门票数为,则,
故,
故的分布列为:
0 1 2
故甲乙两人都没有获得任何门票的概率.
(2)解:由(1)可得:乙获得的门票数比甲多的概率.
【解析】【分析】(1) 由题意结合独立事件乘法求概率公式和对立事件求概率公式可得预定一张开幕式门票不成功的概率,再结合独立事件乘法求概率公式和对立事件求概率公式、互斥事件加法求概率公式得出成功的概率,设甲获得的门票数为,进而得出的可能取值,再利用独立事件乘法求概率公式和对立事件求概率公式、互斥事件加法求概率公式求出随机变量X的分布列,设乙获得的门票数为,则,再结合二项分布求概率公式得出随机变量Y的分布列,再利用独立事件乘法求概率公式得出甲乙两人都没有获得任何门票的概率。
(2) 由(1)结合独立事件乘法求概率公式和互斥事件加法求概率公式,从而得出乙获得的门票数比甲多的概率。
24.【答案】(1)解:线上同学平均分分;
线下同学平均分分;
又200名同学,线上人数占40%,线下人数占60%,
所以所有200名同学的平均分分.
(2)解:线上同学成绩良好人数为人,
线下同学成绩良好人数为人,
所以抽取数学成绩为良好,且,故线下的可能性大.
(3)解:由线下成绩中等同学人数为人,其它同学人,
所以从线下学生中随机抽取10名同学,抽到k个学生的成绩为中等的概率,且,
要使最大,则,即,
所以,则,故.
【解析】【分析】(1)利用已知条件结合频率分布直方图求平均数公式得出这200名学生的数学平均分。
(2)利用已知条件结合频率分布直方图中各小组的矩形的面积等于各小组的频率,再结合比较法判断出线下的可能性大。
(3) 利用已知条件结合频率分布直方图中各小组的频率等于各小组的矩形的面积,再结合频数等于频率乘以样本容量的公式得出线下成绩中等同学人数,进而得出其它同学人数,所以从线下学生中随机抽取10名同学,进而得出抽到k个学生的成绩为中等的概率,且,要使最大,则,进而得出实数k的取值范围,从而得出满足要求的k的值。
25.【答案】(1)解:设:第次通过第一关,:第次通过第二关,甲可以进入第三关的概率为,
由题意知
.
(2)解:设此次闯关活动的分数记为.
①由题意可知,
因为,且,
所以,则;
而,且,
所以前名参赛者的最低得分高于,
而甲的得分为分,所以甲能够获得奖励;
②假设乙所说为真,则,
,
而,所以,
从而,
而,
所以为小概率事件,即丙的分数为430分是小概率事件,可认为其不可能发生,但却又发生了,所以可认为乙所说为假.
【解析】【分析】(1) 设:第次通过第一关,:第次通过第二关, 计算 即可求出甲可以进入第三关的概率;
(2)①由 ,且 ,计算σ ,求出前400名参赛者的最低得分,与甲的得分比较即可;
②假设乙所说为真,由μ=201计算σ ,求出μ+3σ的值与430比较,即可得出结论.
26.【答案】(1)解:记事件A:直径约的结节在1年内发展为恶性肿瘤,事件B:该项无创血液检测的检查结果为阴性,
由题,,,,,,,则
所以患者甲检查结果为阴性的概率为0.8486.
(2)解:,
.
所以患者甲的检查结果为阴性,他的这个结节在1年内发展为恶性肿瘤的概率为0.00035.
(3)解:记参加该项检查的1000位患者中,获得20万元赔付的有X人,
,则,
记保险公司每年在这个项目上的收益为Y元,
,
则,
所以保险公司每年在这个项目上的收益估计为13万元.
【解析】【分析】(1) 利用已知条件结合条件概型求概率公式得出他的这个结节在1年内发展为恶性肿瘤的概率。
(2)利用已知条件结合随机变量X服从二项分布,再结合二项分布求数学期望公式得出X的数学期望, 记保险公司每年在这个项目上的收益为Y元 ,再利用数学期望的性质得出随机变量Y的数学期望。
27.【答案】(1)解:由题意得,击中靶心的频率与0.9接近,故概率约为0.9
(2)解:击中靶心的次数大约为 .
(3)解:由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定击不中靶心.
(4)解:由概率的意义知,不一定.
【解析】【分析】(1)由题意得,击中靶心的频率与0.9接近,再结合频率和概率的关系,从而得出该射击运动员射击一次,击中靶心的概率的值。
(2)利用已知条件结合频数等于频率乘以样本容量的公式,进而得出击中靶心的次数。
(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定击不中靶心。
(4)由概率的意义知第10次不一定击中靶心。
28.【答案】(1)解:记甲袋中红球是r,白球分别为 ,
由题意得顾客A可以从甲袋中先后摸出2个球,其所有等可能出现的结果为:
(r,r),(r, ),(r, ),( ,r),( , ),( , ),( ,r),( , ),( , )共9种,
其中结果(r, ),(r, ),( ,r),( ,r)可获奖金15元,
所以顾客A所获奖金为15元的概率为 .
(2)解:由题意的顾客A可以根据方案a抽奖两次或根据方案a,b各抽奖一次.
由(1)知顾客A根据方案a抽奖两次所获奖金及其概率如下表:
所获奖金(元) 0 15 30
概率
记乙袋中红球分别是R1,R2,白球W
则顾客A根据方案a,b各抽奖一次的所有等可能出现的结果为:
(r,R1),(r,R2),(r,W),( ,R1),( ,R2),( ,W),( ,R1),( ,R2),( ,W)共9种
其中结果(r,R1),(r,R2)可获奖金25元.结果(r,W)可获奖金15元,
( ,R1),( ,R2),( ,W),( ,R1),( ,R2)可获奖金10元,其余可获奖金0元,
所以顾客A根据方案a,b各抽奖一次所获奖金及其概率如下表:
所获奖金(元) 0 10 15 25
概率
由此可知顾客A最有可能获得的奖金数为15元.
【解析】【分析】(1)利用已知条件结合古典概型求概率公式得出其所获奖金为15元的概率。
(2) 利用已知条件结合列举法得出顾客A根据方案a,b各抽奖一次的所有等可能出现的结果,再利用古典概型求概率公式得出顾客A根据方案a,b各抽奖一次所获奖金及其概率,进而得出顾客A最有可能获得的奖金数。
29.【答案】(1)解:记A1表示事件“第2局结果为甲胜”,
A2表示事件“第3局甲参加比赛时,结果为甲负”,
A表示事件“第4局甲当裁判”.
则A=A1·A2.
.
(2)解:记表示事件“第1局结果为乙胜”,
表示事件“第2局乙参加比赛时,结果为乙胜”,
表示事件“第3局乙参加比赛时,结果为乙胜”,
B表示事件“前4局中恰好当1次裁判”.
则.
.
【解析】【分析】(1)设表示事件“第二局结果为甲胜”,表示事件“第三局甲参加比赛结果为负”,A表示事件“甲当裁判”,可得,利用相互独立事件的概率计算公式,即可求解.
(2)记表示事件“第1局结果为乙胜”,表示事件“第2局乙参加比赛时,结果为乙胜”,表示事件“第3局乙参加比赛时,结果为乙胜”,B表示事件“前4局中恰好当1次裁判”,利用相互独立事件的概率公式和互斥事件的概率加法公式,即可求解.
30.【答案】(1)解:设事件“甲第一轮猜对” ,事件“乙第一轮猜对” ,事件C=“甲第二轮猜对” ,事件“乙第二轮猜对 ,
甲、乙两人在两轮竞答活动中答对3题的概率为
解得或(舍去)
;
(2)解:三轮竞答活动中甲乙一共答6题,甲、乙两人在三轮竞答活动中答对4题,即总共有2题没有答对,
可能甲有两题没有答对,可能乙有两题没有答对,可能甲乙各有一题没有答对.
甲、乙两人在三轮竞答活动中答对4题的概率
【解析】【分析】(1)利用已知条件结合独立事件乘法求概率公式、对立事件求概率公式、互斥事件加法求概率公式,进而得出p的值。
(2) 利用已知条件结合二项分布求概率公式和互斥事件加法求概率公式,进而得出甲、乙两人在三轮竞答活动中答对4题的概率。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
