2023-2024学年北师版七上数学5.3+应用一元一次方程——水箱变高了课件(共22张PPT)
文档属性
| 名称 | 2023-2024学年北师版七上数学5.3+应用一元一次方程——水箱变高了课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 820.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 21:06:19 | ||
图片预览








文档简介
(共22张PPT)
第五章一元一次方程
5. 3 水箱变高了
学习目标
分析简单问题中的数量关系,建立方程解决问题。
通过具体问题的解决体会利用方程解决问题的关键是寻找等量关系。
问题引入
某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m.那么在容积不变的前提下,水箱的高度将由原先的4m增高为多少米?
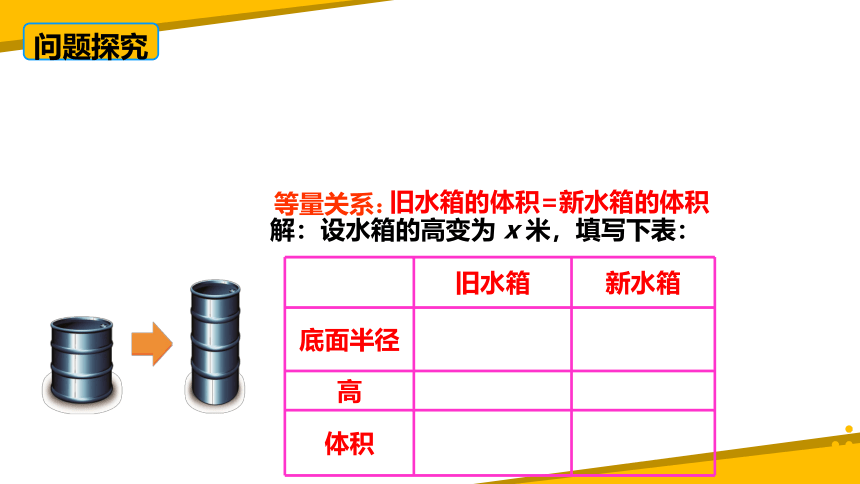
问题探究
等量关系:
旧水箱的体积=新水箱的体积
解:设水箱的高变为 x 米,填写下表:
旧水箱 新水箱
底面半径
高
体积
问题引入
等量关系:
旧水箱的容积=新水箱的容积
解:设水箱的高为 x m,
由题意得 :
解得
答:水箱的高变成了6.25米.
例题讲解
例:用一根长为10米的铁线围成一个长方形.
(1)使得该长方形的长比宽多1.4 米,此时长方形的长、宽各是多少米呢?面积是多少?
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形(1)所围成的长方形相比,面积有什么变化?
(3)使得该长方形的长和宽相等,即围成一个正方形,此时正方形的边长是多少米?围成的面积与(2)所围成的面积相比,又有什么变化?
例题讲解
用一根长为10米的铁线围成一个长方形.
(1)使得该长方形的长比宽多1.4 米,此时长方形的长、宽各是多少米呢?面积是多少?
等量关系:
长+宽=周长的一半
解:(1)设长方形的宽为x米,
则它的 长为 米,
由题意得:
(x +1.4)
x+1.4 +x =
解得:x=1.8
长是:1.8+1.4=3.2(米)
面积:3.2 × 1.8=5.76(米2)
答:长方形的长为3.2米,宽为1.8米,面积是5.76米2.
例题讲解
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形(1)所围成的长方形相比,面积有什么变化?
x
x+0.8
解:设长方形的宽为x米,则它的长为(x+0.8)米.由题意得:
x+0.8 +x =
解得:x=2.1
长为:2.1+0.8=2.9(米)
面积:2.9 ×2.1=6.09(米2)
面积增加:6.09-5.76=0.33(米2)
例题讲解
(3)使得该长方形的长和宽相等,即围成一个正方形,此时正方形的边长是多少米?围成的面积与(2)所围成的面积相比,又有什么变化?
x
解:设正方形的边长为x米.
由题意得:
解得:x=2.5
边长为: 2.5米
面积:2.5 × 2.5 =6. 25 (米2)
面积增加:6.25-6.09=0.16(米2 )
同样长的铁线围成怎样的四边形面积最大呢?
例题讲解
当周长不变时,围成正方形面积最大
随堂练习
1、 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?
10
10
10
6
10
6
中考链接
1.(2023·四川成都·统考中考真题)《孙子算经》是中国古代重要的数学著作,是《算经十书》之一.书中记载了这样一个题目:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?其大意是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,则可列方程为( )
A.
B.
C.
D.
中考链接
2.(2023 吉林)《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱,问合伙人数是多少?
A.
.
.
课堂小结
一 物体锻压或液体更换容器题,体积(或容积)不变。
二 固定长度,虽然围成的图形形状及面积不同,但是应抓住图形的总周长不变。
A.
当堂测试
1.我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一,书中记载一道问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天可以追上慢马?若设快马x天可以追上慢马,则下列方程正确的是( )
A.240x+150x=150×12 B.240x-150x=240×12
C.240x+150x=240×12 D.240x-150x=150×12
A.
当堂测试
2.《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡有x只,可列方程为( )
A.4x+2(94-x)=35 B.4x+2(35-x)=94
C.2x+4(94-x)=35 D.2x+4(35-x)=94
A.
分层作业
【基础达标作业】
1.端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为( )
A.10x+5(x-1)=70 B.10x+5(x+1)=70
C.10(x-1)+5x=70 D.10(x+1)+5x=70
A.
分层作业
【基础达标作业】
2.近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )
A.60件 B.66件 C.68件 D.72件
.
分层作业
【能力提升作业】
3.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x.则列出方程正确的是( )
A.3×2x+5=2x B.3×20x+5=10x×2
C.3×20+x+5=20x D.3×(20+x)+5=10x+2
4.购买一本书,打八折比打九折少花2元钱,那么这本书的原价是( )元。
A.
分层作业
【能力提升作业】
5.湖南省2011年赴台旅游人数达7.6万人.我市某九年级一学生家长准备中考后全家3人去台湾旅游,计划花费20000元。设每人向旅行社缴纳x元费用后,共剩5000元用于购物和品尝台湾美食.根据题意,列出方程为( )
6.某市在端午节准备举行划龙舟大赛,预计15个队共330人参加.已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨.设每条船上划桨的有x人,那么可列出一元一次方程为( )
A.
分层作业
【拓展延伸作业】
7.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:
今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
第五章一元一次方程
5. 3 水箱变高了
学习目标
分析简单问题中的数量关系,建立方程解决问题。
通过具体问题的解决体会利用方程解决问题的关键是寻找等量关系。
问题引入
某居民楼顶有一个底面直径和高均为4m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4m减少为3.2m.那么在容积不变的前提下,水箱的高度将由原先的4m增高为多少米?
问题探究
等量关系:
旧水箱的体积=新水箱的体积
解:设水箱的高变为 x 米,填写下表:
旧水箱 新水箱
底面半径
高
体积
问题引入
等量关系:
旧水箱的容积=新水箱的容积
解:设水箱的高为 x m,
由题意得 :
解得
答:水箱的高变成了6.25米.
例题讲解
例:用一根长为10米的铁线围成一个长方形.
(1)使得该长方形的长比宽多1.4 米,此时长方形的长、宽各是多少米呢?面积是多少?
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形(1)所围成的长方形相比,面积有什么变化?
(3)使得该长方形的长和宽相等,即围成一个正方形,此时正方形的边长是多少米?围成的面积与(2)所围成的面积相比,又有什么变化?
例题讲解
用一根长为10米的铁线围成一个长方形.
(1)使得该长方形的长比宽多1.4 米,此时长方形的长、宽各是多少米呢?面积是多少?
等量关系:
长+宽=周长的一半
解:(1)设长方形的宽为x米,
则它的 长为 米,
由题意得:
(x +1.4)
x+1.4 +x =
解得:x=1.8
长是:1.8+1.4=3.2(米)
面积:3.2 × 1.8=5.76(米2)
答:长方形的长为3.2米,宽为1.8米,面积是5.76米2.
例题讲解
(2)使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形(1)所围成的长方形相比,面积有什么变化?
x
x+0.8
解:设长方形的宽为x米,则它的长为(x+0.8)米.由题意得:
x+0.8 +x =
解得:x=2.1
长为:2.1+0.8=2.9(米)
面积:2.9 ×2.1=6.09(米2)
面积增加:6.09-5.76=0.33(米2)
例题讲解
(3)使得该长方形的长和宽相等,即围成一个正方形,此时正方形的边长是多少米?围成的面积与(2)所围成的面积相比,又有什么变化?
x
解:设正方形的边长为x米.
由题意得:
解得:x=2.5
边长为: 2.5米
面积:2.5 × 2.5 =6. 25 (米2)
面积增加:6.25-6.09=0.16(米2 )
同样长的铁线围成怎样的四边形面积最大呢?
例题讲解
当周长不变时,围成正方形面积最大
随堂练习
1、 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?
10
10
10
6
10
6
中考链接
1.(2023·四川成都·统考中考真题)《孙子算经》是中国古代重要的数学著作,是《算经十书》之一.书中记载了这样一个题目:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?其大意是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,则可列方程为( )
A.
B.
C.
D.
中考链接
2.(2023 吉林)《九章算术》中记载了一道数学问题,其译文为:有人合伙买羊,每人出5钱,还缺45钱;每人出7钱,还缺3钱,问合伙人数是多少?
A.
.
.
课堂小结
一 物体锻压或液体更换容器题,体积(或容积)不变。
二 固定长度,虽然围成的图形形状及面积不同,但是应抓住图形的总周长不变。
A.
当堂测试
1.我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一,书中记载一道问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天可以追上慢马?若设快马x天可以追上慢马,则下列方程正确的是( )
A.240x+150x=150×12 B.240x-150x=240×12
C.240x+150x=240×12 D.240x-150x=150×12
A.
当堂测试
2.《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡有x只,可列方程为( )
A.4x+2(94-x)=35 B.4x+2(35-x)=94
C.2x+4(94-x)=35 D.2x+4(35-x)=94
A.
分层作业
【基础达标作业】
1.端午节买粽子,每个肉粽比素粽多1元,购买10个肉粽和5个素粽共用去70元,设每个肉粽x元,则可列方程为( )
A.10x+5(x-1)=70 B.10x+5(x+1)=70
C.10(x-1)+5x=70 D.10(x+1)+5x=70
A.
分层作业
【基础达标作业】
2.近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )
A.60件 B.66件 C.68件 D.72件
.
分层作业
【能力提升作业】
3.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x.则列出方程正确的是( )
A.3×2x+5=2x B.3×20x+5=10x×2
C.3×20+x+5=20x D.3×(20+x)+5=10x+2
4.购买一本书,打八折比打九折少花2元钱,那么这本书的原价是( )元。
A.
分层作业
【能力提升作业】
5.湖南省2011年赴台旅游人数达7.6万人.我市某九年级一学生家长准备中考后全家3人去台湾旅游,计划花费20000元。设每人向旅行社缴纳x元费用后,共剩5000元用于购物和品尝台湾美食.根据题意,列出方程为( )
6.某市在端午节准备举行划龙舟大赛,预计15个队共330人参加.已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨.设每条船上划桨的有x人,那么可列出一元一次方程为( )
A.
分层作业
【拓展延伸作业】
7.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:
今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
