人教版数学7年级下册 8.3 实际问题与二元一次方程组 课时练(含解析)
文档属性
| 名称 | 人教版数学7年级下册 8.3 实际问题与二元一次方程组 课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 433.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 11:40:41 | ||
图片预览



文档简介
8.3 实际问题与二元一次方程组
8.3.1 和差倍分与配套问题
1.“鸡兔同笼”是我国古代著名的数学趣题之一.大约在1500年前成书的《孙子算经》中,就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔关在一个笼子里,从上面数,有35个头;从下面数,有94条腿,问笼中各有几只鸡和兔?
2.在武汉全力抗击新型冠状病毒肺炎疫情的危急时刻,全国各省纷纷伸出援手,一批批捐赠物资运往武汉,某单位租用物流公司甲、乙两种货车运输捐赠的物资,已知前两批次租用货车的情况如下表(每辆车都满载):
第一次 第二次
甲种货车(单位:辆) 2 5
乙种货车(单位:辆) 3 6
累计运货重量(单位:吨) 104 233
现租用该物流公司3辆甲种货车和5辆乙种货车,一次性刚好运完第三批捐赠物资,若该批捐赠物资的价格为每吨6500元,则该批捐赠物资的总价是多少元?
8.3 实际问题与二元一次方程组
8.3.1 和差倍分与配套问题
1.【解析】设有x只鸡,有y只兔,
根据题意,得解得
答:有23只鸡,有12只兔.
2.【解析】设每辆甲种货车可运货x吨,每辆乙种货车可运货y吨,
依题意得,解得,
第三批捐赠物资的重量为:3x+5y=3×25+5×18=75+90=165(吨),
该批捐赠物资的总价为:165×6500=1072500(元).
答:该批捐赠物资的总价是1072500元.
8.3.2 几何图形与图文信息问题
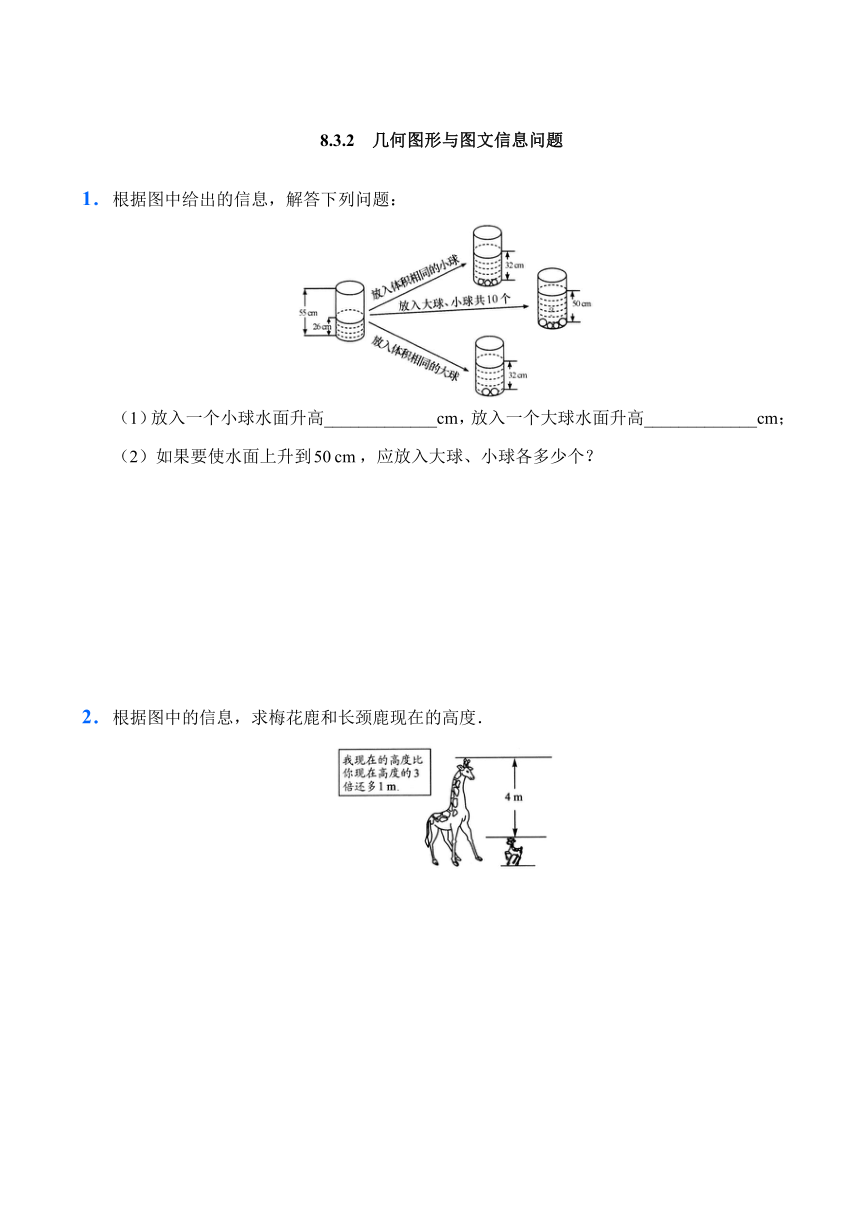
1.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高_____________cm,放入一个大球水面升高_____________cm;
(2)如果要使水面上升到,应放入大球、小球各多少个?
2.根据图中的信息,求梅花鹿和长颈鹿现在的高度.
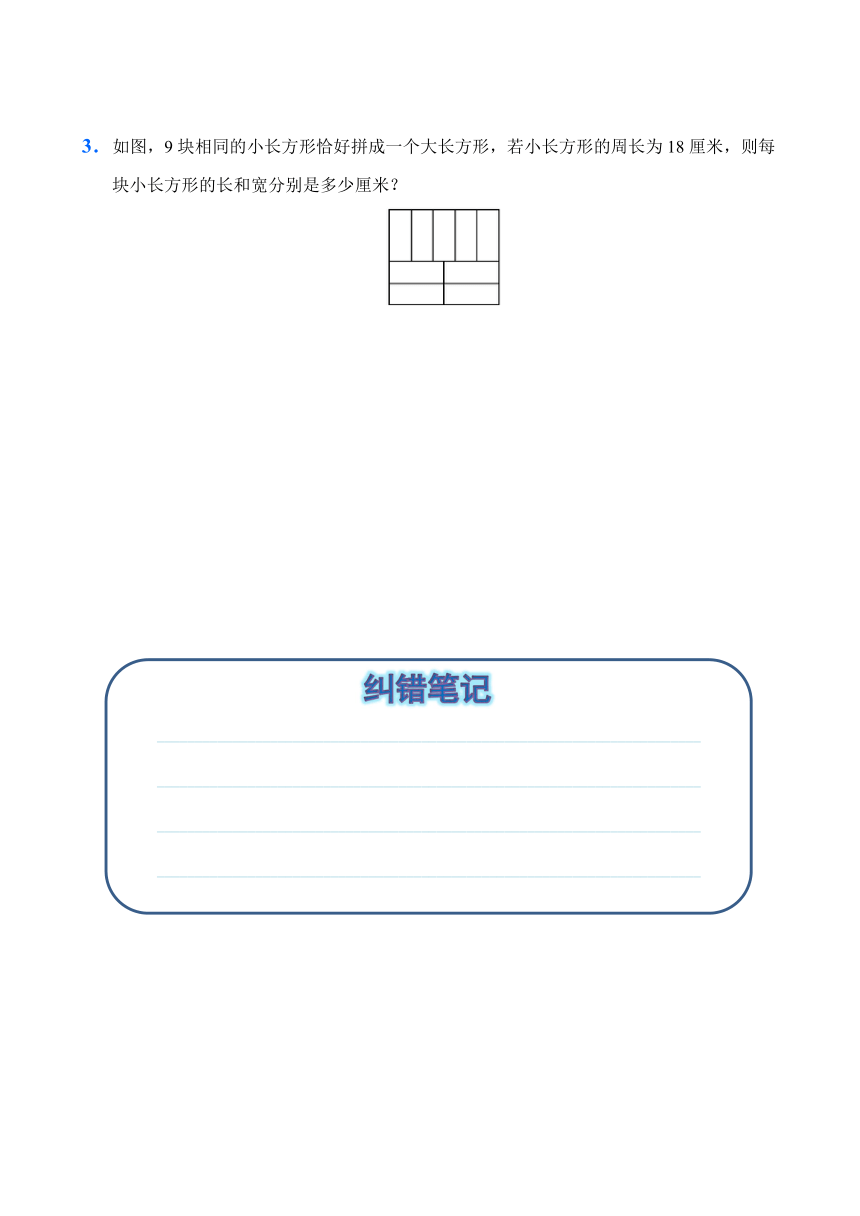
3.如图,9块相同的小长方形恰好拼成一个大长方形,若小长方形的周长为18厘米,则每块小长方形的长和宽分别是多少厘米?
8.3.2 几何图形与图文信息问题
1.【解析】(1)2;3
(2)要使水面上升到,设应放入大球x个、小球y个.
由题意,得,解得.
答:要使水面上升到,应放入大球4个、小球6个.
2.【解析】设梅花鹿和长颈鹿现在的高度分别为x m,y m,
由题意,得,
解得,
答:梅花鹿现在的高度为,长颈鹿现在的高度为.
3.【解析】设每块小长方形的长为x厘米,宽为y厘米,
根据题意,得,
解得,
答:每块小长方形的长为厘米,宽为厘米.
8.3.3 经济生活与行程问题
1.某商场用14 500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表所示:
类别 成本价/(元/箱) 销售价/(元/箱)
甲 25 35
乙 35 48
求:(1)购进甲、乙两种矿泉水各多少箱;
(2)该商场售完这500箱矿泉水,可获利多少元.
2.假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
3.为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,下表是某省的电价标准(每月).例如:方女士家5月份用电,电费二档电价三档电价,共352元;李先生家5月份用电,电费为316元,请问表中二档电价、三档电价各是多少?
阶梯 电量 电价
一档 0.6元
二档 二档电价
三档 及以上 三档电价
8.3.3 经济生活与行程问题
1.【解析】(1)设购进甲矿泉水x箱,购进乙矿泉水y箱,
由题意,得解得
答:购进甲矿泉水300箱,购进乙矿泉水200箱.
(2)(元),
答:该商场售完这500箱矿泉水,可获利5600元.
2.【解析】(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.
由题意得,,解得.
答:出租车的起步价是4.5元,超过1.5千米后每千米收费2元.
(2)(元).
答:小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
3.【解析】设二档电价是x元,三档电价是y元
根据题意,得解得
答:二档电价是0.7元,三档电价是0.9元.
8.3.4 工程问题与其它问题
1.一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元.若先请甲装修组单独做6天,再请乙装修组单独做12天也可以完成,需付两组费用共3480元.
(1)甲、乙两组单独工作一天,商店分别应付多少钱?
(2)单独请哪组,商店所付费用较少?
(3)若装修完后,商店每天可赢利300元,你认为如何安排施工更有利于商店?请你帮助商店作出决策.
2.滴滴快车是一种便捷的出行工具,假设某市的计价规则如下表:
计费项目 里程费 时长费 远途费
单价 1.8元/千米 0.3元/分 0.8元/千米
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7千米以内(含7千米)不收远途费,超过7千米的,超过部分每千米收0.8元.
小王与小张在该市各自乘坐滴滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同.
(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候,已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
8.3.4 工程问题与其它问题
1.【解析】(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元.
由题意得,解得.
答:甲、乙两组单独工作一天,商店分别应付300元和140元.
(2)设工作总量为单位1,甲组工作效率为a(即甲组每天完成工作与工作总量的比值为a),乙组工作效率为b,
根据题意,得,解得,
所以甲组单独完成装修需要12天,乙组单独完成装修需要24天,
所以单独请甲组,需付12×300=3600(元),
单独请乙组,需付24×140=3360(元),
因为3600>3360,所以单独请乙组,商店所付费用较少.
(3)由题意,得
①甲单独做12天完成,需付费用3600元;乙单独做24天完成,需付费用3360元.
但甲组比乙组早12天完工,商店12天的利润为300×12=3600(元),
因为,
所以选择甲组单独做比选择乙组单独做划算.
②甲、乙合作8天完成,需付费用3520元,
甲乙合作比甲单独做早4天完工,商店4天的利润为4×300=1200(元),
因为,
所以甲乙合作比甲单独做划算.
综上所述,应安排甲、乙一起施工,更有利于商店.
2.【解析】(1)设小王与小张乘坐滴滴快车的实际行车时间分别为x分钟,y分钟,
由题意,得:,
所以,
所以,
所以.
答:这两辆滴滴快车的实际行车时间相差19分钟.
(2)由(1)及题意,得
化简,得
,得,所以.
将代入,得.
答:小王的实际乘车时间为37分钟,小张的实际乘车时间为18分钟.
8.3.1 和差倍分与配套问题
1.“鸡兔同笼”是我国古代著名的数学趣题之一.大约在1500年前成书的《孙子算经》中,就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔关在一个笼子里,从上面数,有35个头;从下面数,有94条腿,问笼中各有几只鸡和兔?
2.在武汉全力抗击新型冠状病毒肺炎疫情的危急时刻,全国各省纷纷伸出援手,一批批捐赠物资运往武汉,某单位租用物流公司甲、乙两种货车运输捐赠的物资,已知前两批次租用货车的情况如下表(每辆车都满载):
第一次 第二次
甲种货车(单位:辆) 2 5
乙种货车(单位:辆) 3 6
累计运货重量(单位:吨) 104 233
现租用该物流公司3辆甲种货车和5辆乙种货车,一次性刚好运完第三批捐赠物资,若该批捐赠物资的价格为每吨6500元,则该批捐赠物资的总价是多少元?
8.3 实际问题与二元一次方程组
8.3.1 和差倍分与配套问题
1.【解析】设有x只鸡,有y只兔,
根据题意,得解得
答:有23只鸡,有12只兔.
2.【解析】设每辆甲种货车可运货x吨,每辆乙种货车可运货y吨,
依题意得,解得,
第三批捐赠物资的重量为:3x+5y=3×25+5×18=75+90=165(吨),
该批捐赠物资的总价为:165×6500=1072500(元).
答:该批捐赠物资的总价是1072500元.
8.3.2 几何图形与图文信息问题
1.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高_____________cm,放入一个大球水面升高_____________cm;
(2)如果要使水面上升到,应放入大球、小球各多少个?
2.根据图中的信息,求梅花鹿和长颈鹿现在的高度.
3.如图,9块相同的小长方形恰好拼成一个大长方形,若小长方形的周长为18厘米,则每块小长方形的长和宽分别是多少厘米?
8.3.2 几何图形与图文信息问题
1.【解析】(1)2;3
(2)要使水面上升到,设应放入大球x个、小球y个.
由题意,得,解得.
答:要使水面上升到,应放入大球4个、小球6个.
2.【解析】设梅花鹿和长颈鹿现在的高度分别为x m,y m,
由题意,得,
解得,
答:梅花鹿现在的高度为,长颈鹿现在的高度为.
3.【解析】设每块小长方形的长为x厘米,宽为y厘米,
根据题意,得,
解得,
答:每块小长方形的长为厘米,宽为厘米.
8.3.3 经济生活与行程问题
1.某商场用14 500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表所示:
类别 成本价/(元/箱) 销售价/(元/箱)
甲 25 35
乙 35 48
求:(1)购进甲、乙两种矿泉水各多少箱;
(2)该商场售完这500箱矿泉水,可获利多少元.
2.假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
3.为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,下表是某省的电价标准(每月).例如:方女士家5月份用电,电费二档电价三档电价,共352元;李先生家5月份用电,电费为316元,请问表中二档电价、三档电价各是多少?
阶梯 电量 电价
一档 0.6元
二档 二档电价
三档 及以上 三档电价
8.3.3 经济生活与行程问题
1.【解析】(1)设购进甲矿泉水x箱,购进乙矿泉水y箱,
由题意,得解得
答:购进甲矿泉水300箱,购进乙矿泉水200箱.
(2)(元),
答:该商场售完这500箱矿泉水,可获利5600元.
2.【解析】(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.
由题意得,,解得.
答:出租车的起步价是4.5元,超过1.5千米后每千米收费2元.
(2)(元).
答:小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
3.【解析】设二档电价是x元,三档电价是y元
根据题意,得解得
答:二档电价是0.7元,三档电价是0.9元.
8.3.4 工程问题与其它问题
1.一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元.若先请甲装修组单独做6天,再请乙装修组单独做12天也可以完成,需付两组费用共3480元.
(1)甲、乙两组单独工作一天,商店分别应付多少钱?
(2)单独请哪组,商店所付费用较少?
(3)若装修完后,商店每天可赢利300元,你认为如何安排施工更有利于商店?请你帮助商店作出决策.
2.滴滴快车是一种便捷的出行工具,假设某市的计价规则如下表:
计费项目 里程费 时长费 远途费
单价 1.8元/千米 0.3元/分 0.8元/千米
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7千米以内(含7千米)不收远途费,超过7千米的,超过部分每千米收0.8元.
小王与小张在该市各自乘坐滴滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同.
(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候,已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
8.3.4 工程问题与其它问题
1.【解析】(1)设甲组工作一天商店应付x元,乙组工作一天商店应付y元.
由题意得,解得.
答:甲、乙两组单独工作一天,商店分别应付300元和140元.
(2)设工作总量为单位1,甲组工作效率为a(即甲组每天完成工作与工作总量的比值为a),乙组工作效率为b,
根据题意,得,解得,
所以甲组单独完成装修需要12天,乙组单独完成装修需要24天,
所以单独请甲组,需付12×300=3600(元),
单独请乙组,需付24×140=3360(元),
因为3600>3360,所以单独请乙组,商店所付费用较少.
(3)由题意,得
①甲单独做12天完成,需付费用3600元;乙单独做24天完成,需付费用3360元.
但甲组比乙组早12天完工,商店12天的利润为300×12=3600(元),
因为,
所以选择甲组单独做比选择乙组单独做划算.
②甲、乙合作8天完成,需付费用3520元,
甲乙合作比甲单独做早4天完工,商店4天的利润为4×300=1200(元),
因为,
所以甲乙合作比甲单独做划算.
综上所述,应安排甲、乙一起施工,更有利于商店.
2.【解析】(1)设小王与小张乘坐滴滴快车的实际行车时间分别为x分钟,y分钟,
由题意,得:,
所以,
所以,
所以.
答:这两辆滴滴快车的实际行车时间相差19分钟.
(2)由(1)及题意,得
化简,得
,得,所以.
将代入,得.
答:小王的实际乘车时间为37分钟,小张的实际乘车时间为18分钟.
