第15章 轴对称图形和等腰三角形 小结与复习 课件 (共27张PPT)数学沪科版八年级上册
文档属性
| 名称 | 第15章 轴对称图形和等腰三角形 小结与复习 课件 (共27张PPT)数学沪科版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 22:06:38 | ||
图片预览







文档简介
(共27张PPT)
小结与复习
第 15 章 轴对称图形与
等腰三角形
1.轴对称图形:
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
2.轴对称:
平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.
一、轴对称图形与轴对称
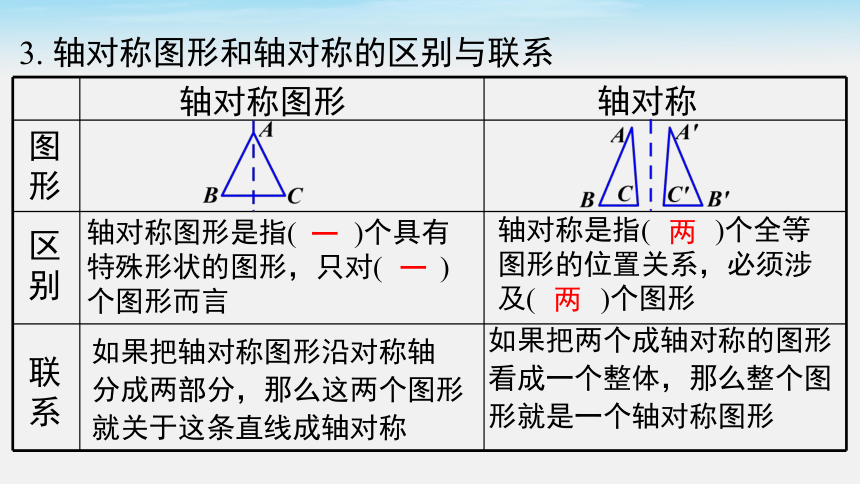
3. 轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
轴对称图形是指( )个具有特殊形状的图形,只对( ) 个图形而言
轴对称是指( )个全等
图形的位置关系,必须涉及( )个图形
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称
如果把两个成轴对称的图形
看成一个整体,那么整个图形就是一个轴对称图形
一
一
两
两
4. 轴对称的性质:
① 如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
② 反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
1. 线段中垂线的性质定理:
线段垂直平分线上的点和线段两端的距离相等.
2. 逆定理:
到线段两端距离相等的点在线段的垂直平分线上.
二、线段的中垂线
1. 定理①:
等腰三角形的两个底角相等.(等边对等角)
2.性质②:
等腰三角形的顶角的平分线垂直平分底边.
(三线合一).
推论:
等边三角形的三个角相等,每个内角都等于 60°.
三、等腰(边)三角形
3.等腰(边)三角形的判定及含 30° 角的直角三角形的性质:
判定定理:
有两个角相等的三角形是等腰三角形(等角对等边).
推论①:三个角都相等的三角形是等边三角形.
推论②:有一个角是 60° 的等腰三角形是等边三角形.
定理:在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半.
1. 性质定理:
角平分线上的点到角两边的距离相等.
2. 判定定理:
角的内部到角两边距离相等的点在角的平分线上.
四、角平分线的性质与判定
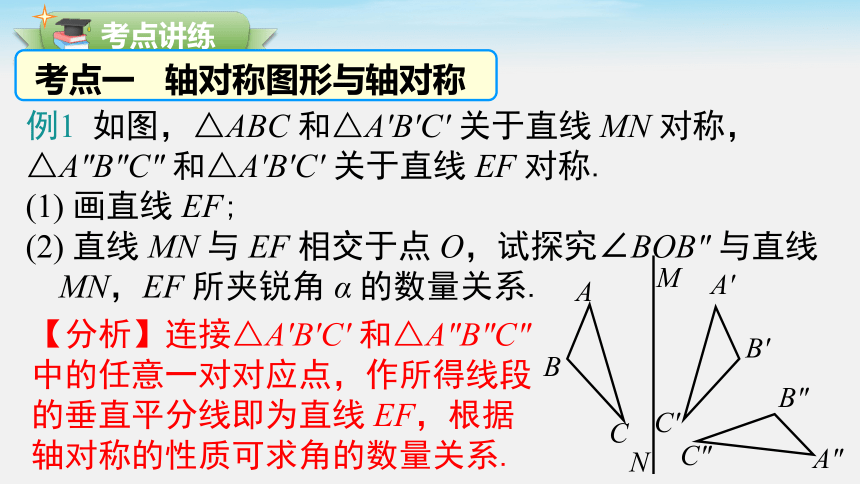
考点一 轴对称图形与轴对称
例1 如图,△ABC 和△A′B′C′ 关于直线 MN 对称,△A″B″C″ 和△A′B′C′ 关于直线 EF 对称.
(1) 画直线 EF;
(2) 直线 MN 与 EF 相交于点 O,试探究∠BOB″ 与直线
MN,EF 所夹锐角 α 的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
M
N
【分析】连接△A′B′C′ 和△A″B″C″中的任意一对对应点,作所得线段的垂直平分线即为直线 EF,根据轴对称的性质可求角的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
解:(1)如图,连接 B′B″,作线段 B′B″ 的垂直平分线EF,则直线 EF 是△A′B′C′ 和△A″B″C″ 的对称轴;
(2)连接 B″O,B′O,BO.
因为 △ABC 和△A′B′C′ 关于直线 MN 对称,
所以∠BOM =∠B′OM.
因为△A″B″C″ 和△A′B′C′
关于直线 EF 对称,
所以∠B′OE =∠B″OE.
所以∠BOB″ = 2(∠B′OM + ∠B′OE)
= 2α.
F
E
O
M
N
轴对称和轴对称图形的概念是本章的重点,通过观察日常生活中的轴对称现象,理解轴对称图形和轴对称的概念的区别与联系;学习轴对称变换,不但要会画一个图形关于某直线的对称图形,还要会进行简单的图案设计,利用轴对称作图确定最短路线等.
方法总结
1. 下面的图形是轴对称图形吗 如果是,你能指出它的对称轴吗
针对训练
2. 如图所示,作出△ABC 关于直线 l 的对称图形.
A
B
C
A′
B′
C′
解:△A′B′C′ 就是所求作的图形.
l
考点二 线段的垂直平分线
例2 如图,AD 是 BC 的垂直平分线,点 C 在 AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB + BD 与 DE 有什么关系?
【分析】运用线段的垂直平分线的性质进行线段之间的转化即可.
A
B
C
D
E
解:∵ AD 是 BC 的垂直平分线,
∴ AB = AC,BD = CD.
∵ 点 C 在 AE 的垂直平分线上,
∴ AC = CE,∴AB = AC = CE.
∴ AB + BD = DE.
3.如图,在△ABC 中,DE 是 AC 的垂直平分线,AC = 5 厘米,△ABD 的周长等于 13 厘米,则△ABC 的周长是 厘米.
18
C
A
B
D
E
常常运用线段的垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”进行线段之间的转换来求线段之间的关系及周长的和差等,有时候与等腰三角形的“三线合一”结合起来考查.
方法总结
针对训练
4.下列说法:
①若点 P、E 是线段 AB 的垂直平分线上两点,则 EA=EB,PA=PB;
②若 PA=PB,EA=EB,则直线 PE 垂直平分线段 AB;
③若 PA=PB,则点 P 必是线段 AB 的垂直平分线上的点;
④若 EA=EB,则经过点 E 的直线垂直平分线段 AB.
其中正确的有 (填序号).
① ② ③
考点三 等腰(等边)三角形的性质与判定
例3 如图所示,在△ABC中,AB = AC,BD⊥AC 于 D.求证: ∠BAC = 2∠DBC.
A
B
C
D
)
)
1
2
E
【分析】根据等腰三角形“三线合一”的性质,可作顶角∠BAC 的平分线,来获取角的数量关系.
证明:作∠BAC 的平分线 AE,交 BC 于点 E,如图,
则
∵ AB = AC,∴ AE⊥BC.
∴∠2 +∠C = 90°.
∵ BD⊥AC,∴∠DBC +∠C = 90°.
∴∠2 =∠DBC.
∴∠BAC = 2∠DBC.
A
B
C
D
)
)
1
2
E
在涉及等腰三角形的有关计算和证明中,常见的辅助线的作法是作顶角的平分线(或底边上的高、中线),然后利用等腰三角形“三线合一”的性质,实现线段或角之间的相互转化.
方法总结
5. 如图,在△ABC 中,AB = AC 时,
(1) ∵ AD⊥BC,
∴∠ ______= ∠_______;_____=_____.
(2) ∵ AD 是中线,
∴____⊥____; ∠______= ∠______.
(3) ∵ AD 是角平分线,
∴____ ⊥____;_____=____.
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
针对训练
例4 如图,在△ABC 中,AD 是角平分线,且 BD = CD,DE⊥AB,DF⊥AC,垂足分别为 E,F.
求证:EB = FC.
A
B
C
D
E
F
【分析】先利用角平分线的性质定理得到 DE = DF,再利用“HL”证明 Rt△BDE≌Rt△CDF.
考点四 角平分线的性质与判定
A
B
C
D
E
F
证明:∵AD 是∠BAC 的角平分线,DE⊥AB,DF⊥AC,
∴ DE = DF,∠DEB =∠DFC = 90°.
在 Rt△BDE 和 Rt△CDF 中,
DE = DF,
BD = CD,
∴ Rt△BDE≌Rt△CDF(HL).
∴ EB = FC.
针对训练
6. 如图,DE⊥AB,DF⊥BG,垂足分别是 E,F, DE = DF, ∠EDB = 60°,则 ∠EBF = °,BE = .
60
BF
E
B
D
F
A
C
G
7.△ABC中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是 .
3
A
B
C
D
E
第6题图
第7题图
8. 如图所示,已知△ABC 中,PE∥AB 交 BC 于点 E,PF∥AC 交 BC 于点 F,点 P 是 AD 上一点,且点 D 到 PE 的距离与到 PF 的距离相等,判断 AD 是否平分∠BAC,并说明理由.
解:AD 平分∠BAC.理由如下:
∵D 到 PE 的距离与到 PF 的距离相等,
∴点 D 在∠EPF 的平分线上.∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4. ∴ AD 平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
线段的垂
直平分线
轴
对
称
角平分线
等腰三角形
轴
对
称
图
形
线段
角
性
质
及
判
定
等腰三角形
等腰三角形的判定:等角对等边.
等边三角形的判定:三个角都相等的三角形是等边三角形;有一个角是 60° 的等腰三角形是等边三角形.
在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半.
见教材章末练习
小结与复习
第 15 章 轴对称图形与
等腰三角形
1.轴对称图形:
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
2.轴对称:
平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.
一、轴对称图形与轴对称
3. 轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
轴对称图形是指( )个具有特殊形状的图形,只对( ) 个图形而言
轴对称是指( )个全等
图形的位置关系,必须涉及( )个图形
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称
如果把两个成轴对称的图形
看成一个整体,那么整个图形就是一个轴对称图形
一
一
两
两
4. 轴对称的性质:
① 如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
② 反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
1. 线段中垂线的性质定理:
线段垂直平分线上的点和线段两端的距离相等.
2. 逆定理:
到线段两端距离相等的点在线段的垂直平分线上.
二、线段的中垂线
1. 定理①:
等腰三角形的两个底角相等.(等边对等角)
2.性质②:
等腰三角形的顶角的平分线垂直平分底边.
(三线合一).
推论:
等边三角形的三个角相等,每个内角都等于 60°.
三、等腰(边)三角形
3.等腰(边)三角形的判定及含 30° 角的直角三角形的性质:
判定定理:
有两个角相等的三角形是等腰三角形(等角对等边).
推论①:三个角都相等的三角形是等边三角形.
推论②:有一个角是 60° 的等腰三角形是等边三角形.
定理:在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半.
1. 性质定理:
角平分线上的点到角两边的距离相等.
2. 判定定理:
角的内部到角两边距离相等的点在角的平分线上.
四、角平分线的性质与判定
考点一 轴对称图形与轴对称
例1 如图,△ABC 和△A′B′C′ 关于直线 MN 对称,△A″B″C″ 和△A′B′C′ 关于直线 EF 对称.
(1) 画直线 EF;
(2) 直线 MN 与 EF 相交于点 O,试探究∠BOB″ 与直线
MN,EF 所夹锐角 α 的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
M
N
【分析】连接△A′B′C′ 和△A″B″C″中的任意一对对应点,作所得线段的垂直平分线即为直线 EF,根据轴对称的性质可求角的数量关系.
A
B
C
A′
B′
C′
A″
B″
C″
解:(1)如图,连接 B′B″,作线段 B′B″ 的垂直平分线EF,则直线 EF 是△A′B′C′ 和△A″B″C″ 的对称轴;
(2)连接 B″O,B′O,BO.
因为 △ABC 和△A′B′C′ 关于直线 MN 对称,
所以∠BOM =∠B′OM.
因为△A″B″C″ 和△A′B′C′
关于直线 EF 对称,
所以∠B′OE =∠B″OE.
所以∠BOB″ = 2(∠B′OM + ∠B′OE)
= 2α.
F
E
O
M
N
轴对称和轴对称图形的概念是本章的重点,通过观察日常生活中的轴对称现象,理解轴对称图形和轴对称的概念的区别与联系;学习轴对称变换,不但要会画一个图形关于某直线的对称图形,还要会进行简单的图案设计,利用轴对称作图确定最短路线等.
方法总结
1. 下面的图形是轴对称图形吗 如果是,你能指出它的对称轴吗
针对训练
2. 如图所示,作出△ABC 关于直线 l 的对称图形.
A
B
C
A′
B′
C′
解:△A′B′C′ 就是所求作的图形.
l
考点二 线段的垂直平分线
例2 如图,AD 是 BC 的垂直平分线,点 C 在 AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB + BD 与 DE 有什么关系?
【分析】运用线段的垂直平分线的性质进行线段之间的转化即可.
A
B
C
D
E
解:∵ AD 是 BC 的垂直平分线,
∴ AB = AC,BD = CD.
∵ 点 C 在 AE 的垂直平分线上,
∴ AC = CE,∴AB = AC = CE.
∴ AB + BD = DE.
3.如图,在△ABC 中,DE 是 AC 的垂直平分线,AC = 5 厘米,△ABD 的周长等于 13 厘米,则△ABC 的周长是 厘米.
18
C
A
B
D
E
常常运用线段的垂直平分线的性质“线段垂直平分线上的点到线段两端的距离相等”进行线段之间的转换来求线段之间的关系及周长的和差等,有时候与等腰三角形的“三线合一”结合起来考查.
方法总结
针对训练
4.下列说法:
①若点 P、E 是线段 AB 的垂直平分线上两点,则 EA=EB,PA=PB;
②若 PA=PB,EA=EB,则直线 PE 垂直平分线段 AB;
③若 PA=PB,则点 P 必是线段 AB 的垂直平分线上的点;
④若 EA=EB,则经过点 E 的直线垂直平分线段 AB.
其中正确的有 (填序号).
① ② ③
考点三 等腰(等边)三角形的性质与判定
例3 如图所示,在△ABC中,AB = AC,BD⊥AC 于 D.求证: ∠BAC = 2∠DBC.
A
B
C
D
)
)
1
2
E
【分析】根据等腰三角形“三线合一”的性质,可作顶角∠BAC 的平分线,来获取角的数量关系.
证明:作∠BAC 的平分线 AE,交 BC 于点 E,如图,
则
∵ AB = AC,∴ AE⊥BC.
∴∠2 +∠C = 90°.
∵ BD⊥AC,∴∠DBC +∠C = 90°.
∴∠2 =∠DBC.
∴∠BAC = 2∠DBC.
A
B
C
D
)
)
1
2
E
在涉及等腰三角形的有关计算和证明中,常见的辅助线的作法是作顶角的平分线(或底边上的高、中线),然后利用等腰三角形“三线合一”的性质,实现线段或角之间的相互转化.
方法总结
5. 如图,在△ABC 中,AB = AC 时,
(1) ∵ AD⊥BC,
∴∠ ______= ∠_______;_____=_____.
(2) ∵ AD 是中线,
∴____⊥____; ∠______= ∠______.
(3) ∵ AD 是角平分线,
∴____ ⊥____;_____=____.
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
针对训练
例4 如图,在△ABC 中,AD 是角平分线,且 BD = CD,DE⊥AB,DF⊥AC,垂足分别为 E,F.
求证:EB = FC.
A
B
C
D
E
F
【分析】先利用角平分线的性质定理得到 DE = DF,再利用“HL”证明 Rt△BDE≌Rt△CDF.
考点四 角平分线的性质与判定
A
B
C
D
E
F
证明:∵AD 是∠BAC 的角平分线,DE⊥AB,DF⊥AC,
∴ DE = DF,∠DEB =∠DFC = 90°.
在 Rt△BDE 和 Rt△CDF 中,
DE = DF,
BD = CD,
∴ Rt△BDE≌Rt△CDF(HL).
∴ EB = FC.
针对训练
6. 如图,DE⊥AB,DF⊥BG,垂足分别是 E,F, DE = DF, ∠EDB = 60°,则 ∠EBF = °,BE = .
60
BF
E
B
D
F
A
C
G
7.△ABC中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是 .
3
A
B
C
D
E
第6题图
第7题图
8. 如图所示,已知△ABC 中,PE∥AB 交 BC 于点 E,PF∥AC 交 BC 于点 F,点 P 是 AD 上一点,且点 D 到 PE 的距离与到 PF 的距离相等,判断 AD 是否平分∠BAC,并说明理由.
解:AD 平分∠BAC.理由如下:
∵D 到 PE 的距离与到 PF 的距离相等,
∴点 D 在∠EPF 的平分线上.∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4. ∴ AD 平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
线段的垂
直平分线
轴
对
称
角平分线
等腰三角形
轴
对
称
图
形
线段
角
性
质
及
判
定
等腰三角形
等腰三角形的判定:等角对等边.
等边三角形的判定:三个角都相等的三角形是等边三角形;有一个角是 60° 的等腰三角形是等边三角形.
在直角三角形中,如果一个锐角等于 30° ,那么它所对的直角边等于斜边的一半.
见教材章末练习
