15.4 第2课时 角平分线的性质及判定 课件 (共34张PPT)数学沪科版八年级上册
文档属性
| 名称 | 15.4 第2课时 角平分线的性质及判定 课件 (共34张PPT)数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 22:05:56 | ||
图片预览



文档简介
(共34张PPT)
第 15 章 轴对称图形与等腰三角形
15.4 角的平分线
第 2 课时 角平分线的性质及判定
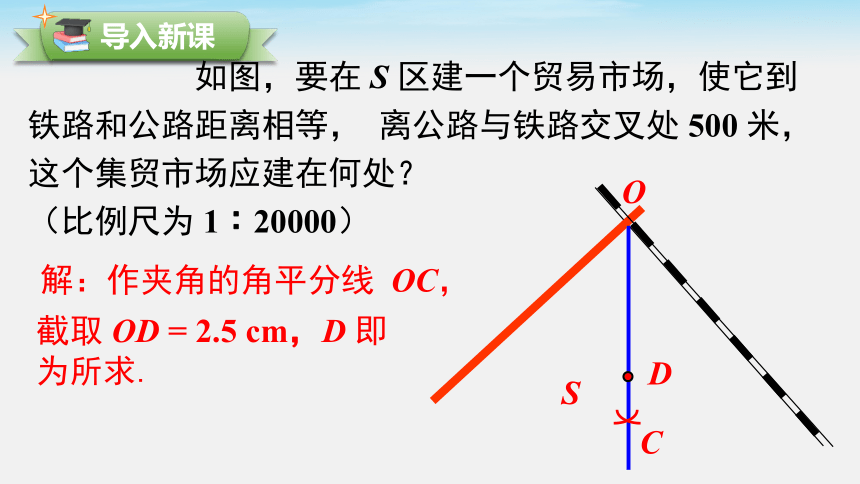
如图,要在 S 区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处 500 米,这个集贸市场应建在何处?
(比例尺为 1︰20000)
D
C
S
解:作夹角的角平分线 OC,
截取 OD = 2.5 cm,D 即为所求.
O
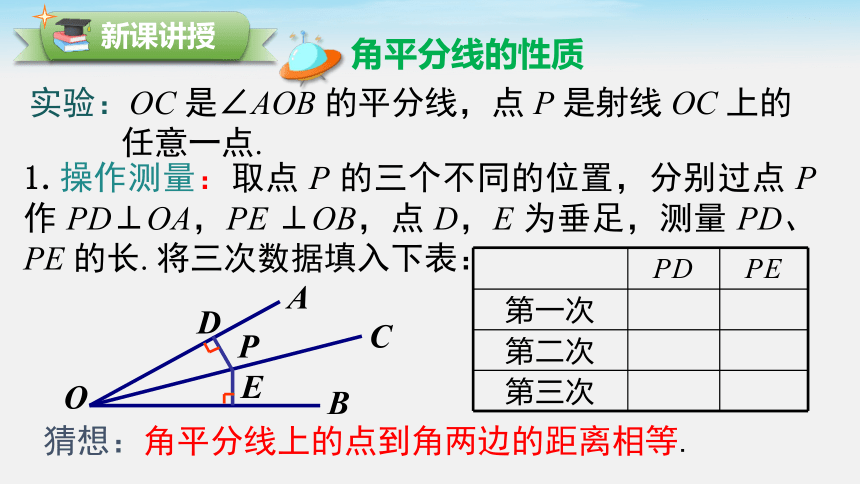
1.操作测量:取点 P 的三个不同的位置,分别过点 P 作 PD⊥OA,PE ⊥OB,点 D,E 为垂足,测量 PD、PE 的长. 将三次数据填入下表:
PD PE
第一次
第二次
第三次
C
O
B
A
P
D
E
实验:OC 是∠AOB 的平分线,点 P 是射线 OC 上的
任意一点.
猜想:角平分线上的点到角两边的距离相等.
角平分线的性质
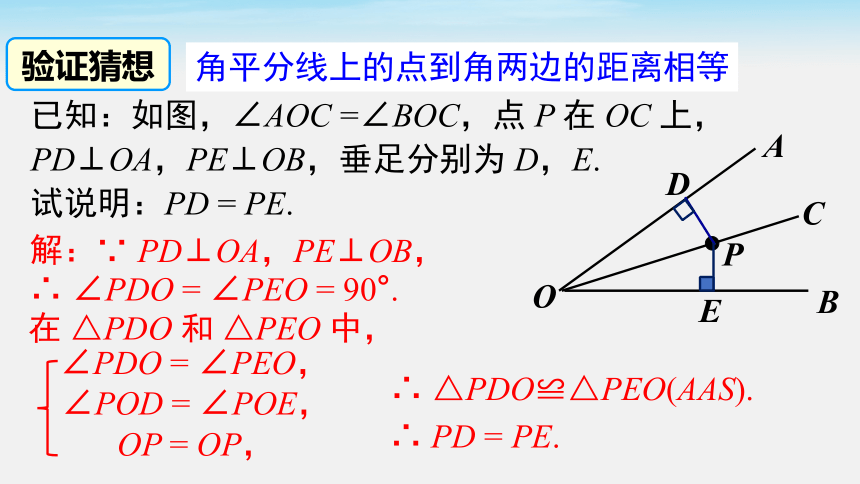
验证猜想
已知:如图,∠AOC =∠BOC,点 P 在 OC 上,PD⊥OA,PE⊥OB,垂足分别为 D,E.
试说明:PD = PE.
P
A
O
B
C
D
E
解:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO = ∠PEO = 90°.
在 △PDO 和 △PEO 中,
∠PDO = ∠PEO,
∠POD = ∠POE,
OP = OP,
∴ △PDO≌△PEO(AAS).
∴ PD = PE.
角平分线上的点到角两边的距离相等
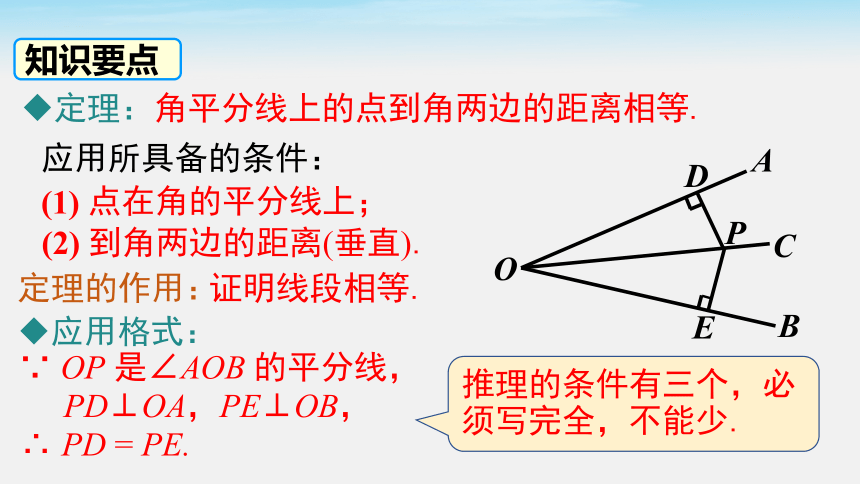
定理:角平分线上的点到角两边的距离相等.
应用所具备的条件:
(1) 点在角的平分线上;
(2) 到角两边的距离(垂直).
定理的作用:
证明线段相等.
知识要点
B
A
D
O
P
E
C
应用格式:
∵ OP 是∠AOB 的平分线,
∴ PD = PE.
PD⊥OA,PE⊥OB,
推理的条件有三个,必须写完全,不能少.
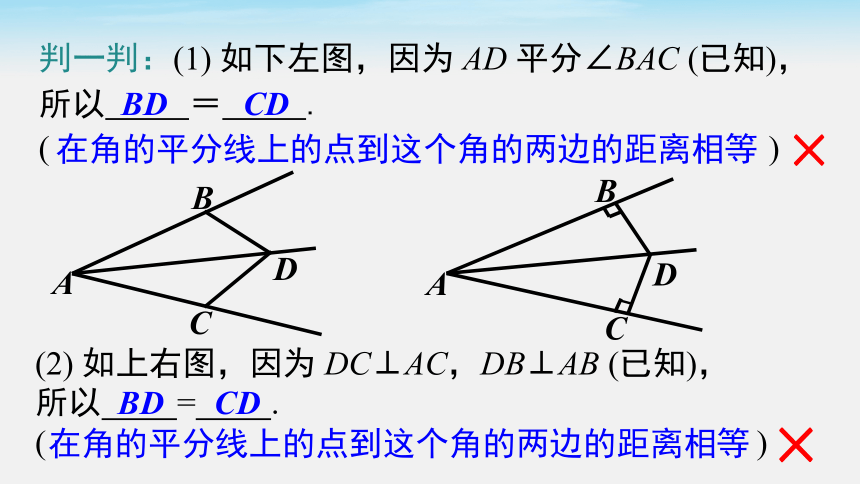
判一判:(1) 如下左图,因为 AD 平分∠BAC (已知),
所以 = .
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2) 如上右图,因为 DC⊥AC,DB⊥AB (已知),
所以 = .
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
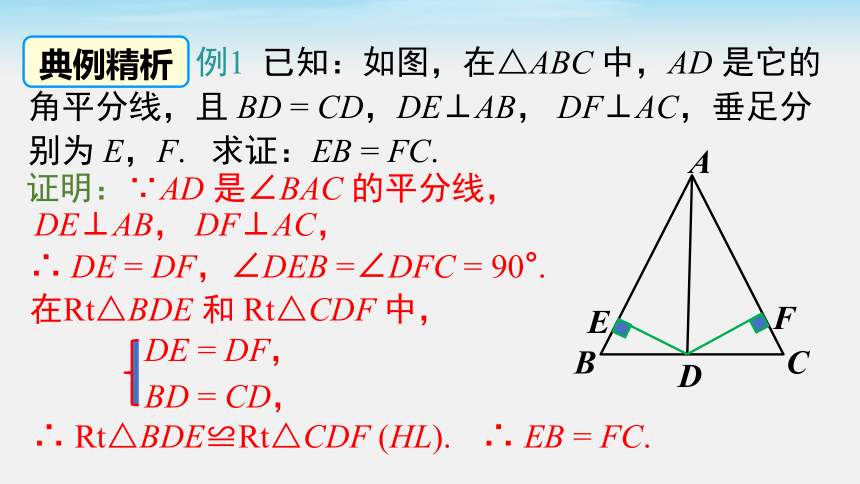
例1 已知:如图,在△ABC 中,AD 是它的角平分线,且 BD = CD,DE⊥AB, DF⊥AC,垂足分别为 E,F. 求证:EB = FC.
A
B
C
D
E
F
证明:∵AD 是∠BAC 的平分线,
DE⊥AB, DF⊥AC,
∴ DE = DF,∠DEB =∠DFC = 90°.
在Rt△BDE 和 Rt△CDF 中,
DE = DF,
BD = CD,
∴ Rt△BDE≌Rt△CDF (HL).
∴ EB = FC.
典例精析
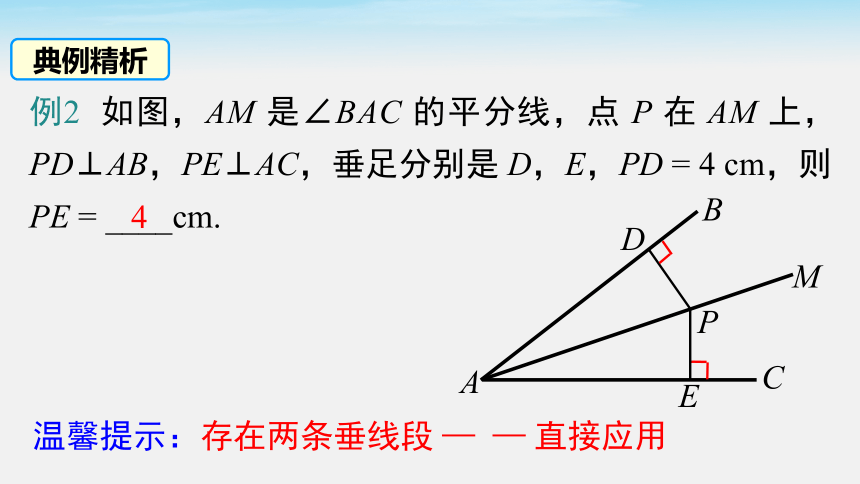
例2 如图,AM 是∠BAC 的平分线,点 P 在 AM 上,PD⊥AB,PE⊥AC,垂足分别是 D,E,PD = 4 cm,则 PE = ____cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段 — — 直接应用
典例精析
变式:如图,在直角△ABC 中,∠C = 90°,AP 平分∠BAC 交 BC 于点 P,若 PC = 4, AB = 14.
(1) 则点 P 到 AB 的距离为_____;
(2) 求 △APB 的面积.
A
B
C
P
D
4
温馨提示:存在一条垂线段 — — 构造应用
故 AB · PD = 28.
解:由角平分线的性质知 PD = PC = 4,
1. 应用角平分线的性质:
存在角平分线
涉及距离问题
2. 联系角平分线的性质:
面积
周长
条件
知识与方法
利用角平分线的性质所得到的等量关系进行转化求解
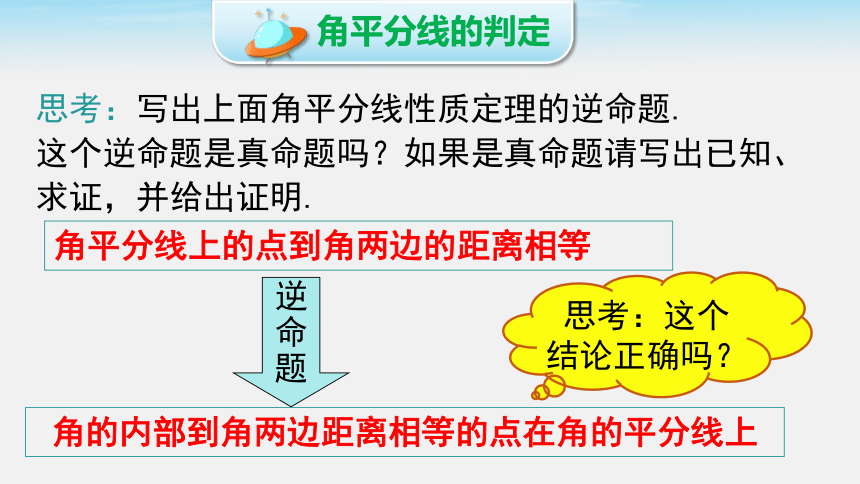
思考:写出上面角平分线性质定理的逆命题.
这个逆命题是真命题吗?如果是真命题请写出已知、求证,并给出证明.
角的内部到角两边距离相等的点在角的平分线上
角平分线上的点到角两边的距离相等
逆
命
题
思考:这个结论正确吗?
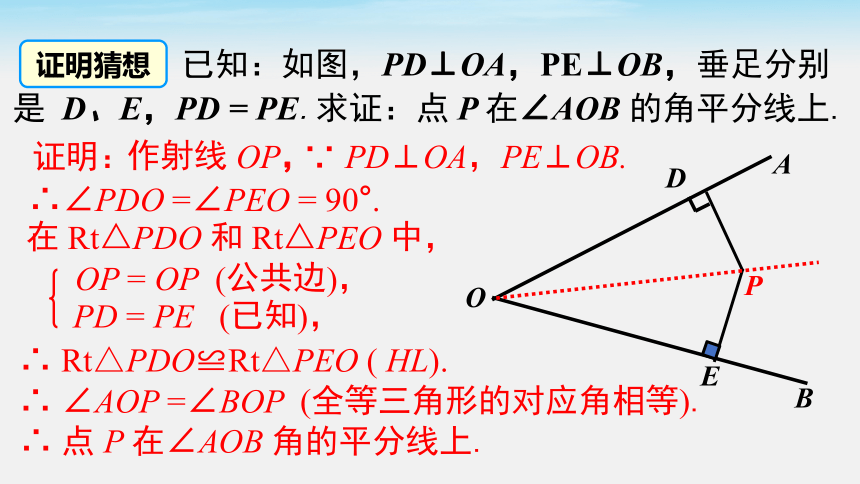
角平分线的判定
已知:如图,PD⊥OA,PE⊥OB,垂足分别是 D、E,PD = PE.求证:点 P 在∠AOB 的角平分线上.
证明猜想
证明:
作射线 OP,
∴ 点 P 在∠AOB 角的平分线上.
在 Rt△PDO 和 Rt△PEO 中,
(全等三角形的对应角相等).
OP = OP (公共边),
PD = PE (已知),
B
A
D
O
P
E
∵ PD⊥OA,PE⊥OB.
∴∠PDO =∠PEO = 90°.
∴ Rt△PDO≌Rt△PEO ( HL).
∴ ∠AOP =∠BOP
角平分线判定定理:
角的内部到角两边距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD = PE.
∴点 P 在 ∠AOB 的平分线上.
知识总结
例3 如图,某地有两所大学和两条交叉的公路.图中点M,N 表示大学,OA,OB 表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相同,到两条公路的距离也相同,你能确定出仓库 P 应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)
O
N
M
A
B
O
N
M
A
B
P
方法总结:到角两边距离相等的点在角的平分线上,到两点距离相等的点在这两点连线的垂直平分线上.
解:如图所示:
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点
三角形的内角平分线
活动2 分别过交点作三角形三边的垂线,用刻度尺量一
量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的 垂线段相等
你能证明这个结论吗?
已知:如图,△ABC 的角平分线 BM,CN 相交于点 P,
求证: (1) 点 P 到三边 AB,BC,CA 的距离相等.
证明结论
证明:过点 P 作 PD,PE,PF 分别垂直于 AB,BC,CA,垂足分别为 D,E,F.
∵BM 是 △ABC 的角平分线,
点 P 在 BM 上,
∴PD = PE. 同理 PE = PF.
∴PD = PE = PF.
即点 P 到三边 AB,BC,CA 的距离相等.
D
E
F
A
B
C
P
N
M
(2) 连接 AP,求证:AP 平分∠BAC.
∵由 (1) 得, PD = PE = PF (已证).
∴ PD = PF (等量代换).
又∵ PD⊥AB,PF⊥AB,
∴ AP 平分∠BAC
(角平分线上的点到角两边的距离相等).
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
D
E
F
A
B
C
P
N
M
变式1:如图,在直角 △ABC 中,AC = BC,∠C =90°,AP 平分∠BAC,BD 平分∠ABC;AP,BD 交于点 O,过点 O 作 OM⊥AC,若 OM = 4,
(1)求点 O 到 △ABC 三边的距离和.
M
E
N
A
B
C
P
O
D
温馨提示:不存在垂线段 — — 构造应用
12
解:连接 OC,
(2)若 △ABC 的周长为 32,求 △ABC 的面积.
M
E
N
A
B
C
P
O
D
2.联系角平分线性质:
距离
面积
周长
知识与方法
1.应用角平分线的判定与性质:
存在角平分线或能判定为角平分线
涉及角平分线上的点到两边的距离问题
条件
例4 如图,在 △ABC 中,点 O 是 △ABC 内一点,且点 O 到 △ABC 三边的距离相等.
若∠A=40°,则 ∠BOC 的度数为 ( ).
A.110° B.120°
C.130° D.140°
A
解析:O 到 △ABC 三边的距离相等,所以 O 是三条内角平分线的交点,AO,BO,CO 都是角平分线,
则∠CBO=∠ABO= ∠ABC,∠BCO=∠ACO= ∠ACB,
∵ ∠ABC+∠ACB=180°-40°=140°,
∴ ∠OBC+∠OCB=70°,
∴ ∠BOC=180°-70°=110°.
由已知,O 到三角形三边的距离相等,得 O 是三条内角平分线的交点,再利用三角形内角和定理即可求出∠BOC 的度数.
方法总结
归纳总结
图形
已知 条件
结论
P
C
P
C
OP 平分∠AOB
PD⊥OA 于 D
PE⊥OB 于 E
PD = PE
OP 平分 ∠AOB
PD = PE
PD⊥OA 于 D
PE⊥OB 于 E
角的平分线的判定
角的平分线的性质
2. △ABC 中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是 .
A
B
C
D
3
E
1. 如图,DE⊥AB,DF⊥BG,垂足分别是 E,F,DE = DF,∠FDB = 60°,则∠EBF = °,BE = .
60
BF
E
B
D
F
A
C
G
解析:过点 D 作 DF⊥AC 于 F,
∵ AD 是△ABC 的角平分线,DE⊥AB.
∴ DF = DE = 2.
解得 AC=3.
4. 如图,AD 是△ABC 的角平分线,DE⊥AB,垂足为 E,S△ABC = 7,DE = 2,AB = 4,则 AC 的长是 ( )
A. 6 B. 5 C. 4 D. 3
D
B
C
E
A
D
F
方法总结:利用角平分线的性质作辅助线构造三角形的高,再利用三角形面积公式求出线段长度是常用的方法.
4. 在 Rt△ABC 中,BD 平分∠ABC,DE⊥AB 于 E,则:
(1) 哪条线段与 DE 相等?为什么?(2) 若 AB=10,
BC=8,AC=6,求 BE,AE 的长和 △AED 的周长.
解:(1) DC=DE.
理由如下:角平分线上的点到角两边的距离相等.
(2) 在 Rt△CDB 和 Rt△EDB 中,DC = DE,DB = DB,∴ Rt△CDB≌Rt△EDB(HL),
∴ BE=BC=8.
∴ AE=AB - BE=2.
∴△AED 的周长为AE + ED + DA=2 + 6=8.
E
D
C
B
A
6
8
10
解:过点 P 作 MN⊥AD 于点 M,交 BC 于点 N.
∵ AD∥BC,
∴ MN⊥BC,MN 为 AD 与 BC 间的距离.
∵ AP 平分∠BAD,PM⊥AD,PE⊥AB,
∴ PM = PE. 同理,PN = PE.
∴ PM = PN = PE =3.
∴ MN = 6, 即 AD 与 BC 之间的距离为 6.
5. 如图,已知 AD∥BC,P 是∠BAD 与∠ABC 的平分线的交点,PE⊥AB 于 E,且 PE = 3. 求 AD 与 BC 间的距离.
6. 已知:如图,OD 平分∠POQ,在 OP,OQ 边上取OA=OB,点 C 在 OD 上,CM⊥AD 于 M,CN⊥BD 于 N. 求证:CM = CN.
证明:∵ OD 平分∠POQ,
∴∠AOD = ∠BOD.
在△AOD 与△BOD 中,
OA = OB,
∠AOD =∠BOD,
OD = OD,
∴△AOD≌△BOD (SAS).
又∵ CM⊥AD ,CN⊥BD ,
∴ CM = CN.
∴∠ADO =∠BDO.
7.如图,已知∠CBD 和∠BCE 的平分线相交于点 F,求证:点 F 在∠DAE 的平分线上.
证明:过点 F 作 FG⊥AE 于 G,FH⊥AD 于 H,FM⊥BC 于 M.
∵点 F 在∠BCE 的平分线上,FG⊥AE, FM⊥BC.
∴FG=FM.
又∵点 F 在∠CBD 的平分线上, FH⊥AD, FM⊥BC,
∴FM=FH.
∴FG=FH.
∴点 F 在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
拓展思维
8. 如图,直线 l1、l2、l3 表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可选择的地址有几处?画出它的位置.
P1
P2
P3
P4
l1
l2
l3
角平分线的性质及判定
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
判定定理
角的内部到角两边距离相等的点在这个角的平分线上
重要结论
三角形的角平分线相交于内部一点
第 15 章 轴对称图形与等腰三角形
15.4 角的平分线
第 2 课时 角平分线的性质及判定
如图,要在 S 区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处 500 米,这个集贸市场应建在何处?
(比例尺为 1︰20000)
D
C
S
解:作夹角的角平分线 OC,
截取 OD = 2.5 cm,D 即为所求.
O
1.操作测量:取点 P 的三个不同的位置,分别过点 P 作 PD⊥OA,PE ⊥OB,点 D,E 为垂足,测量 PD、PE 的长. 将三次数据填入下表:
PD PE
第一次
第二次
第三次
C
O
B
A
P
D
E
实验:OC 是∠AOB 的平分线,点 P 是射线 OC 上的
任意一点.
猜想:角平分线上的点到角两边的距离相等.
角平分线的性质
验证猜想
已知:如图,∠AOC =∠BOC,点 P 在 OC 上,PD⊥OA,PE⊥OB,垂足分别为 D,E.
试说明:PD = PE.
P
A
O
B
C
D
E
解:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO = ∠PEO = 90°.
在 △PDO 和 △PEO 中,
∠PDO = ∠PEO,
∠POD = ∠POE,
OP = OP,
∴ △PDO≌△PEO(AAS).
∴ PD = PE.
角平分线上的点到角两边的距离相等
定理:角平分线上的点到角两边的距离相等.
应用所具备的条件:
(1) 点在角的平分线上;
(2) 到角两边的距离(垂直).
定理的作用:
证明线段相等.
知识要点
B
A
D
O
P
E
C
应用格式:
∵ OP 是∠AOB 的平分线,
∴ PD = PE.
PD⊥OA,PE⊥OB,
推理的条件有三个,必须写完全,不能少.
判一判:(1) 如下左图,因为 AD 平分∠BAC (已知),
所以 = .
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2) 如上右图,因为 DC⊥AC,DB⊥AB (已知),
所以 = .
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
例1 已知:如图,在△ABC 中,AD 是它的角平分线,且 BD = CD,DE⊥AB, DF⊥AC,垂足分别为 E,F. 求证:EB = FC.
A
B
C
D
E
F
证明:∵AD 是∠BAC 的平分线,
DE⊥AB, DF⊥AC,
∴ DE = DF,∠DEB =∠DFC = 90°.
在Rt△BDE 和 Rt△CDF 中,
DE = DF,
BD = CD,
∴ Rt△BDE≌Rt△CDF (HL).
∴ EB = FC.
典例精析
例2 如图,AM 是∠BAC 的平分线,点 P 在 AM 上,PD⊥AB,PE⊥AC,垂足分别是 D,E,PD = 4 cm,则 PE = ____cm.
B
A
C
P
M
D
E
4
温馨提示:存在两条垂线段 — — 直接应用
典例精析
变式:如图,在直角△ABC 中,∠C = 90°,AP 平分∠BAC 交 BC 于点 P,若 PC = 4, AB = 14.
(1) 则点 P 到 AB 的距离为_____;
(2) 求 △APB 的面积.
A
B
C
P
D
4
温馨提示:存在一条垂线段 — — 构造应用
故 AB · PD = 28.
解:由角平分线的性质知 PD = PC = 4,
1. 应用角平分线的性质:
存在角平分线
涉及距离问题
2. 联系角平分线的性质:
面积
周长
条件
知识与方法
利用角平分线的性质所得到的等量关系进行转化求解
思考:写出上面角平分线性质定理的逆命题.
这个逆命题是真命题吗?如果是真命题请写出已知、求证,并给出证明.
角的内部到角两边距离相等的点在角的平分线上
角平分线上的点到角两边的距离相等
逆
命
题
思考:这个结论正确吗?
角平分线的判定
已知:如图,PD⊥OA,PE⊥OB,垂足分别是 D、E,PD = PE.求证:点 P 在∠AOB 的角平分线上.
证明猜想
证明:
作射线 OP,
∴ 点 P 在∠AOB 角的平分线上.
在 Rt△PDO 和 Rt△PEO 中,
(全等三角形的对应角相等).
OP = OP (公共边),
PD = PE (已知),
B
A
D
O
P
E
∵ PD⊥OA,PE⊥OB.
∴∠PDO =∠PEO = 90°.
∴ Rt△PDO≌Rt△PEO ( HL).
∴ ∠AOP =∠BOP
角平分线判定定理:
角的内部到角两边距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD = PE.
∴点 P 在 ∠AOB 的平分线上.
知识总结
例3 如图,某地有两所大学和两条交叉的公路.图中点M,N 表示大学,OA,OB 表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相同,到两条公路的距离也相同,你能确定出仓库 P 应该建在什么位置吗?请在图中画出你的设计.(尺规作图,不写作法,保留作图痕迹)
O
N
M
A
B
O
N
M
A
B
P
方法总结:到角两边距离相等的点在角的平分线上,到两点距离相等的点在这两点连线的垂直平分线上.
解:如图所示:
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点
三角形的内角平分线
活动2 分别过交点作三角形三边的垂线,用刻度尺量一
量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的 垂线段相等
你能证明这个结论吗?
已知:如图,△ABC 的角平分线 BM,CN 相交于点 P,
求证: (1) 点 P 到三边 AB,BC,CA 的距离相等.
证明结论
证明:过点 P 作 PD,PE,PF 分别垂直于 AB,BC,CA,垂足分别为 D,E,F.
∵BM 是 △ABC 的角平分线,
点 P 在 BM 上,
∴PD = PE. 同理 PE = PF.
∴PD = PE = PF.
即点 P 到三边 AB,BC,CA 的距离相等.
D
E
F
A
B
C
P
N
M
(2) 连接 AP,求证:AP 平分∠BAC.
∵由 (1) 得, PD = PE = PF (已证).
∴ PD = PF (等量代换).
又∵ PD⊥AB,PF⊥AB,
∴ AP 平分∠BAC
(角平分线上的点到角两边的距离相等).
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
D
E
F
A
B
C
P
N
M
变式1:如图,在直角 △ABC 中,AC = BC,∠C =90°,AP 平分∠BAC,BD 平分∠ABC;AP,BD 交于点 O,过点 O 作 OM⊥AC,若 OM = 4,
(1)求点 O 到 △ABC 三边的距离和.
M
E
N
A
B
C
P
O
D
温馨提示:不存在垂线段 — — 构造应用
12
解:连接 OC,
(2)若 △ABC 的周长为 32,求 △ABC 的面积.
M
E
N
A
B
C
P
O
D
2.联系角平分线性质:
距离
面积
周长
知识与方法
1.应用角平分线的判定与性质:
存在角平分线或能判定为角平分线
涉及角平分线上的点到两边的距离问题
条件
例4 如图,在 △ABC 中,点 O 是 △ABC 内一点,且点 O 到 △ABC 三边的距离相等.
若∠A=40°,则 ∠BOC 的度数为 ( ).
A.110° B.120°
C.130° D.140°
A
解析:O 到 △ABC 三边的距离相等,所以 O 是三条内角平分线的交点,AO,BO,CO 都是角平分线,
则∠CBO=∠ABO= ∠ABC,∠BCO=∠ACO= ∠ACB,
∵ ∠ABC+∠ACB=180°-40°=140°,
∴ ∠OBC+∠OCB=70°,
∴ ∠BOC=180°-70°=110°.
由已知,O 到三角形三边的距离相等,得 O 是三条内角平分线的交点,再利用三角形内角和定理即可求出∠BOC 的度数.
方法总结
归纳总结
图形
已知 条件
结论
P
C
P
C
OP 平分∠AOB
PD⊥OA 于 D
PE⊥OB 于 E
PD = PE
OP 平分 ∠AOB
PD = PE
PD⊥OA 于 D
PE⊥OB 于 E
角的平分线的判定
角的平分线的性质
2. △ABC 中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是 .
A
B
C
D
3
E
1. 如图,DE⊥AB,DF⊥BG,垂足分别是 E,F,DE = DF,∠FDB = 60°,则∠EBF = °,BE = .
60
BF
E
B
D
F
A
C
G
解析:过点 D 作 DF⊥AC 于 F,
∵ AD 是△ABC 的角平分线,DE⊥AB.
∴ DF = DE = 2.
解得 AC=3.
4. 如图,AD 是△ABC 的角平分线,DE⊥AB,垂足为 E,S△ABC = 7,DE = 2,AB = 4,则 AC 的长是 ( )
A. 6 B. 5 C. 4 D. 3
D
B
C
E
A
D
F
方法总结:利用角平分线的性质作辅助线构造三角形的高,再利用三角形面积公式求出线段长度是常用的方法.
4. 在 Rt△ABC 中,BD 平分∠ABC,DE⊥AB 于 E,则:
(1) 哪条线段与 DE 相等?为什么?(2) 若 AB=10,
BC=8,AC=6,求 BE,AE 的长和 △AED 的周长.
解:(1) DC=DE.
理由如下:角平分线上的点到角两边的距离相等.
(2) 在 Rt△CDB 和 Rt△EDB 中,DC = DE,DB = DB,∴ Rt△CDB≌Rt△EDB(HL),
∴ BE=BC=8.
∴ AE=AB - BE=2.
∴△AED 的周长为AE + ED + DA=2 + 6=8.
E
D
C
B
A
6
8
10
解:过点 P 作 MN⊥AD 于点 M,交 BC 于点 N.
∵ AD∥BC,
∴ MN⊥BC,MN 为 AD 与 BC 间的距离.
∵ AP 平分∠BAD,PM⊥AD,PE⊥AB,
∴ PM = PE. 同理,PN = PE.
∴ PM = PN = PE =3.
∴ MN = 6, 即 AD 与 BC 之间的距离为 6.
5. 如图,已知 AD∥BC,P 是∠BAD 与∠ABC 的平分线的交点,PE⊥AB 于 E,且 PE = 3. 求 AD 与 BC 间的距离.
6. 已知:如图,OD 平分∠POQ,在 OP,OQ 边上取OA=OB,点 C 在 OD 上,CM⊥AD 于 M,CN⊥BD 于 N. 求证:CM = CN.
证明:∵ OD 平分∠POQ,
∴∠AOD = ∠BOD.
在△AOD 与△BOD 中,
OA = OB,
∠AOD =∠BOD,
OD = OD,
∴△AOD≌△BOD (SAS).
又∵ CM⊥AD ,CN⊥BD ,
∴ CM = CN.
∴∠ADO =∠BDO.
7.如图,已知∠CBD 和∠BCE 的平分线相交于点 F,求证:点 F 在∠DAE 的平分线上.
证明:过点 F 作 FG⊥AE 于 G,FH⊥AD 于 H,FM⊥BC 于 M.
∵点 F 在∠BCE 的平分线上,FG⊥AE, FM⊥BC.
∴FG=FM.
又∵点 F 在∠CBD 的平分线上, FH⊥AD, FM⊥BC,
∴FM=FH.
∴FG=FH.
∴点 F 在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
拓展思维
8. 如图,直线 l1、l2、l3 表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可选择的地址有几处?画出它的位置.
P1
P2
P3
P4
l1
l2
l3
角平分线的性质及判定
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
判定定理
角的内部到角两边距离相等的点在这个角的平分线上
重要结论
三角形的角平分线相交于内部一点
