15.1 第1课时 轴对称图形与轴对称 课件 (共39张PPT)数学沪科版八年级上册
文档属性
| 名称 | 15.1 第1课时 轴对称图形与轴对称 课件 (共39张PPT)数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 22:08:34 | ||
图片预览









文档简介
(共39张PPT)
第 15 章 轴对称图形与等腰三角形
15.1 轴对称图形
第 1 课时 轴对称图形与轴对称
水天一色,相映成辉
它们有什么共同的特点?
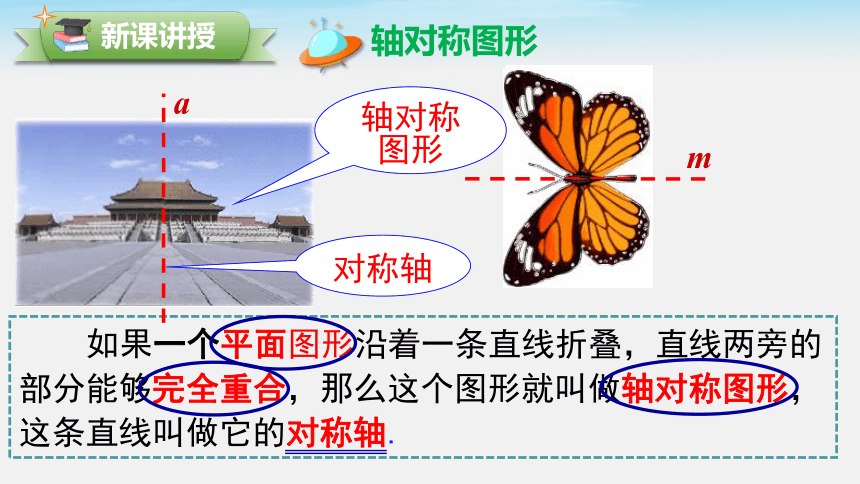
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
轴对称图形
对称轴
a
m
轴对称图形
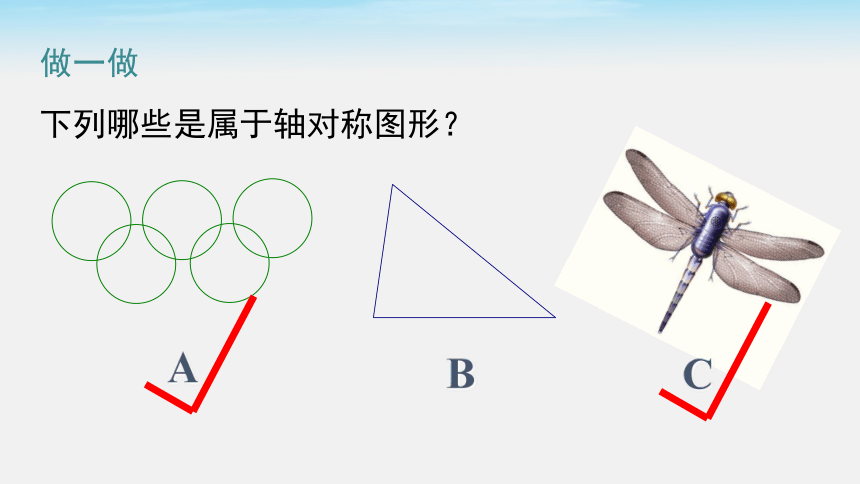
做一做
下列哪些是属于轴对称图形?
A
B
C
你能举出一些轴对称图形的例子吗?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
游戏规则: 每人轮流按顺序报一个字母,如果你认为你所报的字母的形状是一个轴对称图形,你就迅速站起来报是,并说出它有几条对称轴;如果你认为你报的字母的形状不是轴对称图形,那么,你只需坐在座位上报不是就可以了. 其他同学认真听,如果报错了,及时提醒.
全班总动员
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
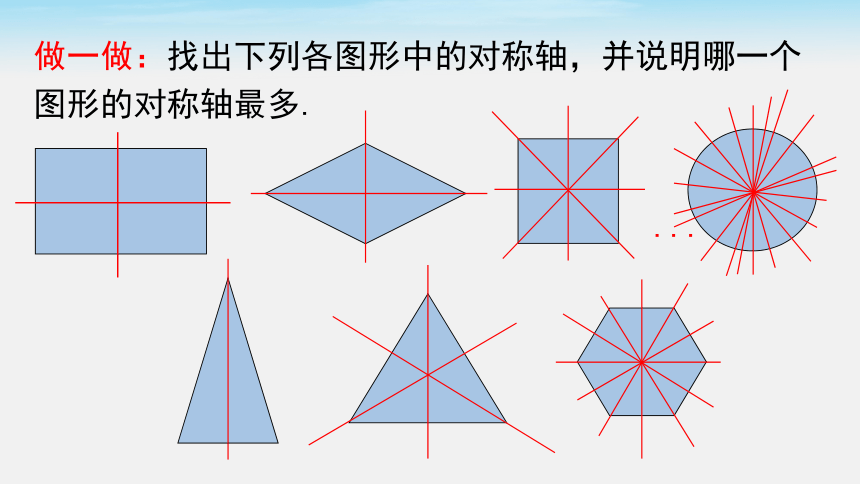
做一做:找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
...
想一想:下面的每对图形有什么共同特点?
A′
A
B
C
B′
C′
对称轴
平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点(叫做对称点).
对称轴
例 下列四组图片中有哪几组图形成轴对称?
B
D
C
A
典例精析
知识要点
比较归纳
轴对称图形 两个图形成轴对称
图形
区别
联系 两个有特殊位置关系的全等图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
一个图形具有的特殊形状
6
6
这是轴对称图形还是两个图形成轴对称?说说你的理由.
观察与思考
1. 动画 (1) 中的两个三角形有什么关系?
2. 动画 (2) 中的三角形是个什么图形?
(1)
(2)
性质:轴对称变换不改变图形的形状和大小.
轴对称变换的性质
思考:如图,△ABC 和△A′B′C′ 关于直线 MN 对称,点 A′,B′,C′ 分别是点 A,B,C 的对称点,线段 AA′,BB′,CC′ 与直线 MN 有什么关系?O1A 与 O1A′ 的长度有何关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
O1A = O1A′
O1
如图,MN⊥AA′, AP = A′P.
直线 MN 是线段 AA′ 的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
知识要点
线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,又叫做线段的中垂线.
图形轴对称的性质
一个轴对称图形的对称轴是否也具有上述性质呢?请你自己找一些轴对称图形来检验吧!
反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
知识要点
轴对称图形的性质
A
B
A′
B′
M
N
如图,MN 垂直平分 AA ′,MN 垂直平分 BB ′.
例1 如图,一种滑翔伞的形状是左右成轴对称的四边形 ABCD,其中∠BAD = 150°,∠B = 40°,则∠BCD 的度数是 ( )
A.130° B.150°
C.40° D.65°
解析:因为这种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
所以∠BAC=∠DAC=75°,∠BCA=∠DCA.
所以∠BCA=180°-75°-40°=65°. 所以∠BCD=130°.
A
典例精析
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
例2 如图,正方形 ABCD 的边长为 4 cm,则图中阴影部分的面积为( )
A.4 cm2 B.8 cm2
C.12 cm2 D.16 cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形 ABCD 面积的一半.因为正方形 ABCD 的边长为 4 cm,所以 S阴影=42÷2=8 (cm2). 故选 B.
B
方法归纳:正方形是轴对称图形.在轴对称图形中求不规则的阴影部分面积时,一般可以考虑利用轴对称变换,将其转化为规则图形后再计算面积.
问题1:如何画一个点关于某条直线的轴对称图形?
画出点 A 关于直线 l 的对称点 A′.
﹒
l
A
﹒
A′
O
作法:
(1) 过点 A 作 l 的垂线,垂足为点 O;
(2) 在垂线上 l 的另一侧截取 OA′ = OA.
则点 A′ 就是点 A 关于直线 l 的对称点.
互动探究
作轴对称图形
问题2:如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A′
A′
A′
B′
(B′)
B′
想一想:如果有一个图形(如三角形、四边形)和一条直线,如何画出这个图形关于这条直线对称的图形呢?
例3 如图,已知△ABC 和直线 l,作出与△ABC关于直线 l 对称的图形.
A
B
C
分析:△ABC 可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线 l 的对应点,连接这些对称点,就能得到要画的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点.
(3) 连接 A′B′,B′C′,C′A′,得到的
△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C 关于直线 l 的对称点 B′,C′.
A
B
C
A′
B′
C′
O
方法归纳
作轴对称图形的方法
几何图形都可以看作由点组成的.对于某些图形,只要作出图形中一些特殊点(如线段的端点,三角形、四边形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
例4 在 3×3 的正方形格点图中,有格点△ABC 和△DEF,且△ABC 和△DEF 关于某直线成轴对称,
请在下面给出的图中画出 4 个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
1.下列表情图中,属于轴对称图形的是( )
D
2. 下列图形,对称轴最多的是( )
A.长方形
B.正方形
C.角
D.圆
D
3. 如图,△ABC 与△DEF 关于直线 MN 轴对称,
则以下结论中错误的是( )
A.AB∥DF
B.∠B = ∠E
C.AB = DE
D.AD 的连线被 MN 垂直平分
A
A
B
C
D
E
F
N
M
4. 如图,Rt△ABC 中,∠ACB = 90°,∠A = 50°,将其折叠,使点 A 落在边 CB 上 A′ 处,折痕为 CD,则∠A′DB 的度数为______.
10°
A
D
C
A′
B
5. 如图,把下列图形补成关于直线 l 的对称图形.
解:(1) 整个图形是轴对称图形,对称轴如图所示.
(2) 图中红色的三角形与左上和右下的三角形成轴对称.
(3) 可以.上下两个图形成轴对称,左右两个图形成轴对称.
6. (1) 整个图形是轴对称图形吗?对称轴是什么?
(2) 图中红色的三角形与哪些三角形成轴对称?
(3) 图形可以看作某两个图形成轴对称吗?
7.想一想:一辆汽车的车牌在水中的倒影如图所示,你能确定该车的车牌号码吗
轴对称
轴对称
轴对称图形
定义
性质
定义
性质
画轴对称图形
原理
方法
线段的垂直平分线
对称轴是对称点连线段的垂直平分线
(1)找特征点
(2)作垂线
(3)截取等长
(4)依次连线
第 15 章 轴对称图形与等腰三角形
15.1 轴对称图形
第 1 课时 轴对称图形与轴对称
水天一色,相映成辉
它们有什么共同的特点?
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
轴对称图形
对称轴
a
m
轴对称图形
做一做
下列哪些是属于轴对称图形?
A
B
C
你能举出一些轴对称图形的例子吗?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
游戏规则: 每人轮流按顺序报一个字母,如果你认为你所报的字母的形状是一个轴对称图形,你就迅速站起来报是,并说出它有几条对称轴;如果你认为你报的字母的形状不是轴对称图形,那么,你只需坐在座位上报不是就可以了. 其他同学认真听,如果报错了,及时提醒.
全班总动员
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
做一做:找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
...
想一想:下面的每对图形有什么共同特点?
A′
A
B
C
B′
C′
对称轴
平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点(叫做对称点).
对称轴
例 下列四组图片中有哪几组图形成轴对称?
B
D
C
A
典例精析
知识要点
比较归纳
轴对称图形 两个图形成轴对称
图形
区别
联系 两个有特殊位置关系的全等图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
一个图形具有的特殊形状
6
6
这是轴对称图形还是两个图形成轴对称?说说你的理由.
观察与思考
1. 动画 (1) 中的两个三角形有什么关系?
2. 动画 (2) 中的三角形是个什么图形?
(1)
(2)
性质:轴对称变换不改变图形的形状和大小.
轴对称变换的性质
思考:如图,△ABC 和△A′B′C′ 关于直线 MN 对称,点 A′,B′,C′ 分别是点 A,B,C 的对称点,线段 AA′,BB′,CC′ 与直线 MN 有什么关系?O1A 与 O1A′ 的长度有何关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
O1A = O1A′
O1
如图,MN⊥AA′, AP = A′P.
直线 MN 是线段 AA′ 的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
知识要点
线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,又叫做线段的中垂线.
图形轴对称的性质
一个轴对称图形的对称轴是否也具有上述性质呢?请你自己找一些轴对称图形来检验吧!
反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
知识要点
轴对称图形的性质
A
B
A′
B′
M
N
如图,MN 垂直平分 AA ′,MN 垂直平分 BB ′.
例1 如图,一种滑翔伞的形状是左右成轴对称的四边形 ABCD,其中∠BAD = 150°,∠B = 40°,则∠BCD 的度数是 ( )
A.130° B.150°
C.40° D.65°
解析:因为这种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
所以∠BAC=∠DAC=75°,∠BCA=∠DCA.
所以∠BCA=180°-75°-40°=65°. 所以∠BCD=130°.
A
典例精析
方法归纳:轴对称是一种全等变换,在轴对称图形中求角度时,一般先根据轴对称的性质及已知条件,得出相关角的度数,然后再结合多边形的内角和或三角形外角的性质求解.
例2 如图,正方形 ABCD 的边长为 4 cm,则图中阴影部分的面积为( )
A.4 cm2 B.8 cm2
C.12 cm2 D.16 cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形 ABCD 面积的一半.因为正方形 ABCD 的边长为 4 cm,所以 S阴影=42÷2=8 (cm2). 故选 B.
B
方法归纳:正方形是轴对称图形.在轴对称图形中求不规则的阴影部分面积时,一般可以考虑利用轴对称变换,将其转化为规则图形后再计算面积.
问题1:如何画一个点关于某条直线的轴对称图形?
画出点 A 关于直线 l 的对称点 A′.
﹒
l
A
﹒
A′
O
作法:
(1) 过点 A 作 l 的垂线,垂足为点 O;
(2) 在垂线上 l 的另一侧截取 OA′ = OA.
则点 A′ 就是点 A 关于直线 l 的对称点.
互动探究
作轴对称图形
问题2:如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A′
A′
A′
B′
(B′)
B′
想一想:如果有一个图形(如三角形、四边形)和一条直线,如何画出这个图形关于这条直线对称的图形呢?
例3 如图,已知△ABC 和直线 l,作出与△ABC关于直线 l 对称的图形.
A
B
C
分析:△ABC 可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线 l 的对应点,连接这些对称点,就能得到要画的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点.
(3) 连接 A′B′,B′C′,C′A′,得到的
△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C 关于直线 l 的对称点 B′,C′.
A
B
C
A′
B′
C′
O
方法归纳
作轴对称图形的方法
几何图形都可以看作由点组成的.对于某些图形,只要作出图形中一些特殊点(如线段的端点,三角形、四边形的顶点等)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
例4 在 3×3 的正方形格点图中,有格点△ABC 和△DEF,且△ABC 和△DEF 关于某直线成轴对称,
请在下面给出的图中画出 4 个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
方法归纳:作一个图形关于一条已知直线的对称图形,关键是作出图形上一些点关于这条直线的对称点,然后再根据已知图形将这些点连接起来.
1.下列表情图中,属于轴对称图形的是( )
D
2. 下列图形,对称轴最多的是( )
A.长方形
B.正方形
C.角
D.圆
D
3. 如图,△ABC 与△DEF 关于直线 MN 轴对称,
则以下结论中错误的是( )
A.AB∥DF
B.∠B = ∠E
C.AB = DE
D.AD 的连线被 MN 垂直平分
A
A
B
C
D
E
F
N
M
4. 如图,Rt△ABC 中,∠ACB = 90°,∠A = 50°,将其折叠,使点 A 落在边 CB 上 A′ 处,折痕为 CD,则∠A′DB 的度数为______.
10°
A
D
C
A′
B
5. 如图,把下列图形补成关于直线 l 的对称图形.
解:(1) 整个图形是轴对称图形,对称轴如图所示.
(2) 图中红色的三角形与左上和右下的三角形成轴对称.
(3) 可以.上下两个图形成轴对称,左右两个图形成轴对称.
6. (1) 整个图形是轴对称图形吗?对称轴是什么?
(2) 图中红色的三角形与哪些三角形成轴对称?
(3) 图形可以看作某两个图形成轴对称吗?
7.想一想:一辆汽车的车牌在水中的倒影如图所示,你能确定该车的车牌号码吗
轴对称
轴对称
轴对称图形
定义
性质
定义
性质
画轴对称图形
原理
方法
线段的垂直平分线
对称轴是对称点连线段的垂直平分线
(1)找特征点
(2)作垂线
(3)截取等长
(4)依次连线
