14.2.6 全等三角形的判定方法的综合运用 课件 (共21张PPT)数学沪科版八年级上册
文档属性
| 名称 | 14.2.6 全等三角形的判定方法的综合运用 课件 (共21张PPT)数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第 14 章 全等三角形
14.2 三角形全等的判定
第 6 课时 全等三角形的判定方法的综合运用
问题1 判定两个三角形全等除了定义以外,我们还学习了哪些方法?
(1)“SAS”:两边及其夹角对应相等的两个三角形全等;
(2)“ASA”:两角及其夹边对应相等的两个三角形全等;
(3)“SSS”:三边对应相等的两个三角形全等;
(4)“AAS”:两角及其一角对边对应相等的两个三角形全等;
(5)“HL”:斜边和一直角边对应相等的两个直角三角形全等.
问题2 全等三角形有什么性质?
(1) 全等三角形对应角相等、对应边相等;
(2) 全等三角形的面积、周长相等.
思考:结合全等三角形的性质及全等三角形的判定,你能说说如何证明两条线段(或角)相等?
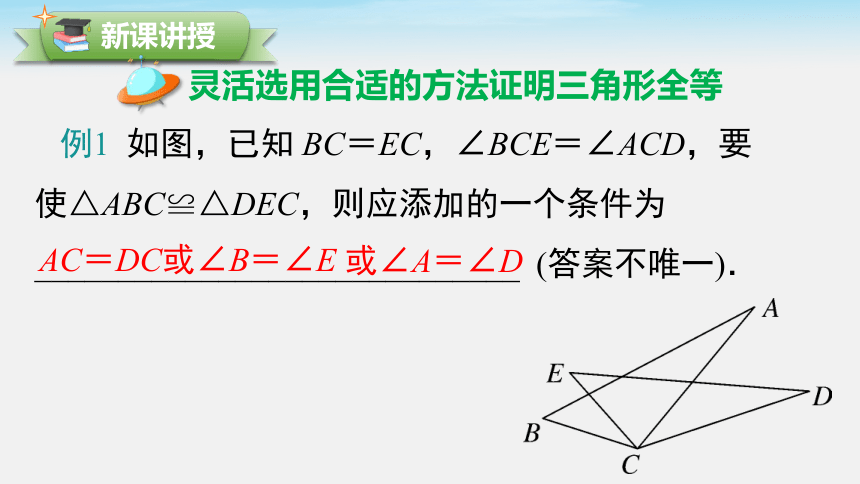
例1 如图,已知 BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为_____________________________ (答案不唯一).
或∠A=∠D
AC=DC或∠B=∠E
灵活选用合适的方法证明三角形全等
解析:根据已知可知两个三角形已经具备有一角与一边对应相等,所以根据全等三角形的判定方法,可以添加一边或一角都可以得到这两个三角形全等.
若根据“SAS”判定时,则可以添加 AC=DC;
若根据“ASA”判定时,则可以添加∠B=∠E;
若根据“AAS”判定时,则可以添加∠A=∠D.
(1)已知一边一角,可任意添加一个角的条件,用 AAS 或 ASA 判定全等;添加边的条件时只能添加夹这个角的边,用 SAS 判定全等.若添加另一边即这个角的对边,符合 SSA 的情形,不一定能判定三角形全等;
(2) 添加条件时,应结合判定图形和五种方法:
SSS、SAS、ASA、AAS、HL,注意除直角三角形外不能是 SSA.
方法归纳
例2 已知:如图,AB = CD ,BC = DA,E,F 是 AC 上的两点,且 AE = CF. 求证:BF = DE.
D
C
A
B
E
F
1
2
证明:在△ABC 和△CDA 中,
AB = CD (已知),
BC = DA (已知),
CA = AC (公共边),
∴△ABC≌△CDA (SSS).
∴∠1 = ∠2 (全等三角形的对应角相等).
多次运用三角形全等的判定
BC = DA (已知),∠1 =∠2 (已知),
CF = AE (已知),
∴ △BCF≌△DAE (SAS).
∴ BF = DE(全等三角形的对应角相等).
在△BCF 和△DAE 中
D
C
A
B
E
F
1
2
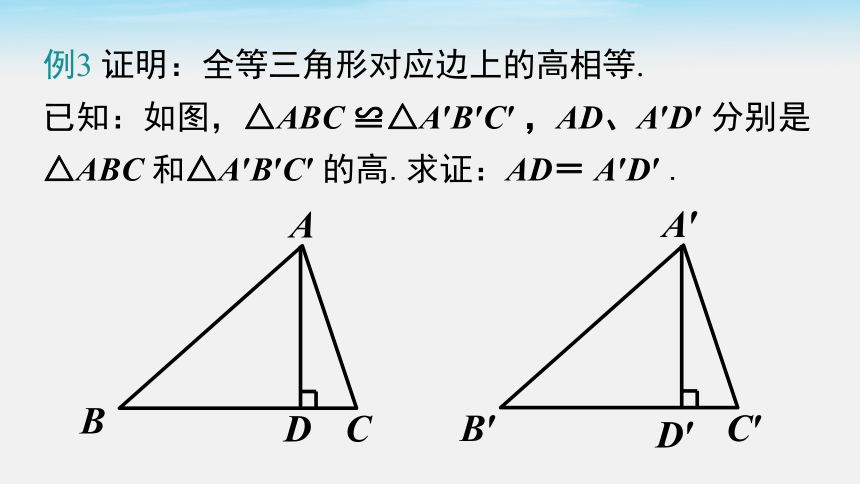
例3 证明:全等三角形对应边上的高相等.
已知:如图,△ABC ≌△A′B′C′ ,AD、A′D′ 分别是△ABC 和△A′B′C′ 的高.求证:AD= A′D′ .
A
B
C
D
A′
B′
C′
D′
证:∵△ABC≌△A′B′C′ ,
∴ AB = A'B'(全等三角形对应边相等),∠ABD =∠A'B'D'(全等三角形对应角相等).
∵ AD⊥BC,A'D'⊥B'C',
∴∠ADB =∠A'D'B'.
在△ABD 和△A'B'D' 中,
∠ADB =∠A'D'B'(已证),
∠ABD =∠A'B'D'(已证),
AB = AB(已证),
∴△ABD≌△A'B'D'(AAS). ∴ AD = A'D'.
A
B
C
D
A′
B′
C′
D′
解:相等.理由如下:在△ABC 和△ADC 中,AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(SSS),∴∠DAE=∠BAE.
在△ADE 和△ABE 中,
AD=AB,∠DAE=∠BAE,AE=AE,
∴△ADE≌△ABE(SAS). ∴DE=BE.
例4 如图,在四边形 ABCD 中,AB=AD,BC=DC,E 为 AC 上的一动点(不与 A 重合),在点 E 移动的过程中 BE 和 DE 是否相等?若相等,请写出证明过程;若不相等,请说明理由.
本题考查了全等三角形的判定和性质,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.本题要特别注意“SSA”不能作为全等三角形一种证明方法使用.
方法总结
C
M
N
A
B
D
例5 如图,已知 CA = CB,AD = BD,M,N 分别是 CA,CB 的中点,求证:DM = DN.
在△ABD 与△CBD 中
CA = CB (已知)
AD = BD (已知)
CD = CD (公共边)
∴△ACD≌△BCD(SSS).
证明:连接 CD,如图所示.
∴∠A = ∠B.
又∵ M,N 分别是 CA,CB 的中点,
∴ AM = BN.
在△AMD 与△BND 中,
AM = BN (已证),
∠A =∠B (已证),
AD = BD (已知),
∴△AMD≌△BND (SAS).
∴ DM = DN.
C
M
N
A
B
D
1.如图,已知 AC = DB,∠ACB =∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC =∠ ,AB = ;
A
B
C
D
DCB
SAS
DCB
DC
2.已知:如图,AB = AC,AD 是△ABC 的角平分线,
求证:BD = CD.
证明:∵AD 是△ABC 的角平分线,
∴ ∠BAD =∠CAD.
在△ABD 和△ACD 中,
AB = AC
∠BAD =∠CAD
AD = AD
∴△ABD≌△ACD (SAS).
(已知),
(已证),
(已证),
∴ BD = CD.
B
C
A
D
已知:如图,AB = AC,BD = CD,
求证: ∠BAD = ∠CAD.
证明:
∴∠BAD =∠CAD.
在△ABD 和△ACD 中,
∴△ABD≌△ACD (SSS).
AB = AC
BD = CD
AD = AD
(已知),
(公共边),
(已知),
B
C
A
D
变式1
已知:如图,AB = AC,BD = CD,E 为 AD 上一点,
求证: BE = CE.
B
C
A
D
∴ ∠BAD =∠CAD.
在△ABD 和△ACD 中,
AB = AC
BD = CD
AD = AD
(已知),
(公共边),
(已知),
∴ BE = CE.
在△ABE 和△ACE 中,
AB = AC
∠BAD =∠CAD
AE = AE
(已知),
(公共边),
(已证),
∴△ABD≌△ACD (SSS).
∴△ABE≌△ACE(SAS).
变式2
E
3. 如图,CD⊥AB 于 D 点,BE⊥AC 于 E 点,BE,CD交于 O 点,且 AO 平分∠BAC.求证:OB=OC.
证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO 平分∠BAC,
∴∠1=∠2.
在△AOD 和△AOE 中,
∴△AOD≌△AOE(AAS).
∴ OD=OE.
∠ADC=∠AEB,
∠1=∠2,
OA=OA,
∠BDC=∠CEB,
∠BOD=∠COE,
OD=OE,
在△BOD 和△COE 中,
∴△BOD≌△COE(ASA).
∴ OB=OC.
判定三角形全等的思路
已知两边
已知一边一角
已知两角
找夹角(SAS)
找另一边(SSS)
找任一角(AAS)
边为角的对边
边为角的一边
找夹角的另一边(SAS)
找边的对角(AAS)
找夹角的另一角(ASA)
找夹边(ASA)
找除夹边外的任意一边(AAS)
第 14 章 全等三角形
14.2 三角形全等的判定
第 6 课时 全等三角形的判定方法的综合运用
问题1 判定两个三角形全等除了定义以外,我们还学习了哪些方法?
(1)“SAS”:两边及其夹角对应相等的两个三角形全等;
(2)“ASA”:两角及其夹边对应相等的两个三角形全等;
(3)“SSS”:三边对应相等的两个三角形全等;
(4)“AAS”:两角及其一角对边对应相等的两个三角形全等;
(5)“HL”:斜边和一直角边对应相等的两个直角三角形全等.
问题2 全等三角形有什么性质?
(1) 全等三角形对应角相等、对应边相等;
(2) 全等三角形的面积、周长相等.
思考:结合全等三角形的性质及全等三角形的判定,你能说说如何证明两条线段(或角)相等?
例1 如图,已知 BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为_____________________________ (答案不唯一).
或∠A=∠D
AC=DC或∠B=∠E
灵活选用合适的方法证明三角形全等
解析:根据已知可知两个三角形已经具备有一角与一边对应相等,所以根据全等三角形的判定方法,可以添加一边或一角都可以得到这两个三角形全等.
若根据“SAS”判定时,则可以添加 AC=DC;
若根据“ASA”判定时,则可以添加∠B=∠E;
若根据“AAS”判定时,则可以添加∠A=∠D.
(1)已知一边一角,可任意添加一个角的条件,用 AAS 或 ASA 判定全等;添加边的条件时只能添加夹这个角的边,用 SAS 判定全等.若添加另一边即这个角的对边,符合 SSA 的情形,不一定能判定三角形全等;
(2) 添加条件时,应结合判定图形和五种方法:
SSS、SAS、ASA、AAS、HL,注意除直角三角形外不能是 SSA.
方法归纳
例2 已知:如图,AB = CD ,BC = DA,E,F 是 AC 上的两点,且 AE = CF. 求证:BF = DE.
D
C
A
B
E
F
1
2
证明:在△ABC 和△CDA 中,
AB = CD (已知),
BC = DA (已知),
CA = AC (公共边),
∴△ABC≌△CDA (SSS).
∴∠1 = ∠2 (全等三角形的对应角相等).
多次运用三角形全等的判定
BC = DA (已知),∠1 =∠2 (已知),
CF = AE (已知),
∴ △BCF≌△DAE (SAS).
∴ BF = DE(全等三角形的对应角相等).
在△BCF 和△DAE 中
D
C
A
B
E
F
1
2
例3 证明:全等三角形对应边上的高相等.
已知:如图,△ABC ≌△A′B′C′ ,AD、A′D′ 分别是△ABC 和△A′B′C′ 的高.求证:AD= A′D′ .
A
B
C
D
A′
B′
C′
D′
证:∵△ABC≌△A′B′C′ ,
∴ AB = A'B'(全等三角形对应边相等),∠ABD =∠A'B'D'(全等三角形对应角相等).
∵ AD⊥BC,A'D'⊥B'C',
∴∠ADB =∠A'D'B'.
在△ABD 和△A'B'D' 中,
∠ADB =∠A'D'B'(已证),
∠ABD =∠A'B'D'(已证),
AB = AB(已证),
∴△ABD≌△A'B'D'(AAS). ∴ AD = A'D'.
A
B
C
D
A′
B′
C′
D′
解:相等.理由如下:在△ABC 和△ADC 中,AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(SSS),∴∠DAE=∠BAE.
在△ADE 和△ABE 中,
AD=AB,∠DAE=∠BAE,AE=AE,
∴△ADE≌△ABE(SAS). ∴DE=BE.
例4 如图,在四边形 ABCD 中,AB=AD,BC=DC,E 为 AC 上的一动点(不与 A 重合),在点 E 移动的过程中 BE 和 DE 是否相等?若相等,请写出证明过程;若不相等,请说明理由.
本题考查了全等三角形的判定和性质,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.本题要特别注意“SSA”不能作为全等三角形一种证明方法使用.
方法总结
C
M
N
A
B
D
例5 如图,已知 CA = CB,AD = BD,M,N 分别是 CA,CB 的中点,求证:DM = DN.
在△ABD 与△CBD 中
CA = CB (已知)
AD = BD (已知)
CD = CD (公共边)
∴△ACD≌△BCD(SSS).
证明:连接 CD,如图所示.
∴∠A = ∠B.
又∵ M,N 分别是 CA,CB 的中点,
∴ AM = BN.
在△AMD 与△BND 中,
AM = BN (已证),
∠A =∠B (已证),
AD = BD (已知),
∴△AMD≌△BND (SAS).
∴ DM = DN.
C
M
N
A
B
D
1.如图,已知 AC = DB,∠ACB =∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC =∠ ,AB = ;
A
B
C
D
DCB
SAS
DCB
DC
2.已知:如图,AB = AC,AD 是△ABC 的角平分线,
求证:BD = CD.
证明:∵AD 是△ABC 的角平分线,
∴ ∠BAD =∠CAD.
在△ABD 和△ACD 中,
AB = AC
∠BAD =∠CAD
AD = AD
∴△ABD≌△ACD (SAS).
(已知),
(已证),
(已证),
∴ BD = CD.
B
C
A
D
已知:如图,AB = AC,BD = CD,
求证: ∠BAD = ∠CAD.
证明:
∴∠BAD =∠CAD.
在△ABD 和△ACD 中,
∴△ABD≌△ACD (SSS).
AB = AC
BD = CD
AD = AD
(已知),
(公共边),
(已知),
B
C
A
D
变式1
已知:如图,AB = AC,BD = CD,E 为 AD 上一点,
求证: BE = CE.
B
C
A
D
∴ ∠BAD =∠CAD.
在△ABD 和△ACD 中,
AB = AC
BD = CD
AD = AD
(已知),
(公共边),
(已知),
∴ BE = CE.
在△ABE 和△ACE 中,
AB = AC
∠BAD =∠CAD
AE = AE
(已知),
(公共边),
(已证),
∴△ABD≌△ACD (SSS).
∴△ABE≌△ACE(SAS).
变式2
E
3. 如图,CD⊥AB 于 D 点,BE⊥AC 于 E 点,BE,CD交于 O 点,且 AO 平分∠BAC.求证:OB=OC.
证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO 平分∠BAC,
∴∠1=∠2.
在△AOD 和△AOE 中,
∴△AOD≌△AOE(AAS).
∴ OD=OE.
∠ADC=∠AEB,
∠1=∠2,
OA=OA,
∠BDC=∠CEB,
∠BOD=∠COE,
OD=OE,
在△BOD 和△COE 中,
∴△BOD≌△COE(ASA).
∴ OB=OC.
判定三角形全等的思路
已知两边
已知一边一角
已知两角
找夹角(SAS)
找另一边(SSS)
找任一角(AAS)
边为角的对边
边为角的一边
找夹角的另一边(SAS)
找边的对角(AAS)
找夹角的另一角(ASA)
找夹边(ASA)
找除夹边外的任意一边(AAS)
