2007年全国各地中考试题压轴题精选全解之五
文档属性
| 名称 | 2007年全国各地中考试题压轴题精选全解之五 |  | |
| 格式 | rar | ||
| 文件大小 | 753.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-17 21:35:00 | ||
图片预览



文档简介
2007年全国各地中考试题压轴题精选全解之五
82.(四川省德阳市)25.如图,已知与轴交于点和的抛物线的顶点为,抛物线与关于轴对称,顶点为.
(1)求抛物线的函数关系式;
(2)已知原点,定点,上的点与上的点始终关于轴对称,则当点运动到何处时,以点为顶点的四边形是平行四边形?
(3)在上是否存在点,使是以为斜边且一个角为的直角三角形?若存,求出点的坐标;若不存在,说明理由.
解:(1)由题意知点的坐标为.
设的函数关系式为.
又点在抛物线上,
,解得.
抛物线的函数关系式为(或).
(2)与始终关于轴对称,
与轴平行.
设点的横坐标为,则其纵坐标为,
,,即.
当时,解得.
当时,解得.
当点运动到或或或时,
,以点为顶点的四边形是平行四边形.
(3)满足条件的点不存在.理由如下:若存在满足条件的点在上,则
,(或),
.
过点作于点,可得.
,,.
点的坐标为.
但是,当时,.
不存在这样的点构成满足条件的直角三角形.
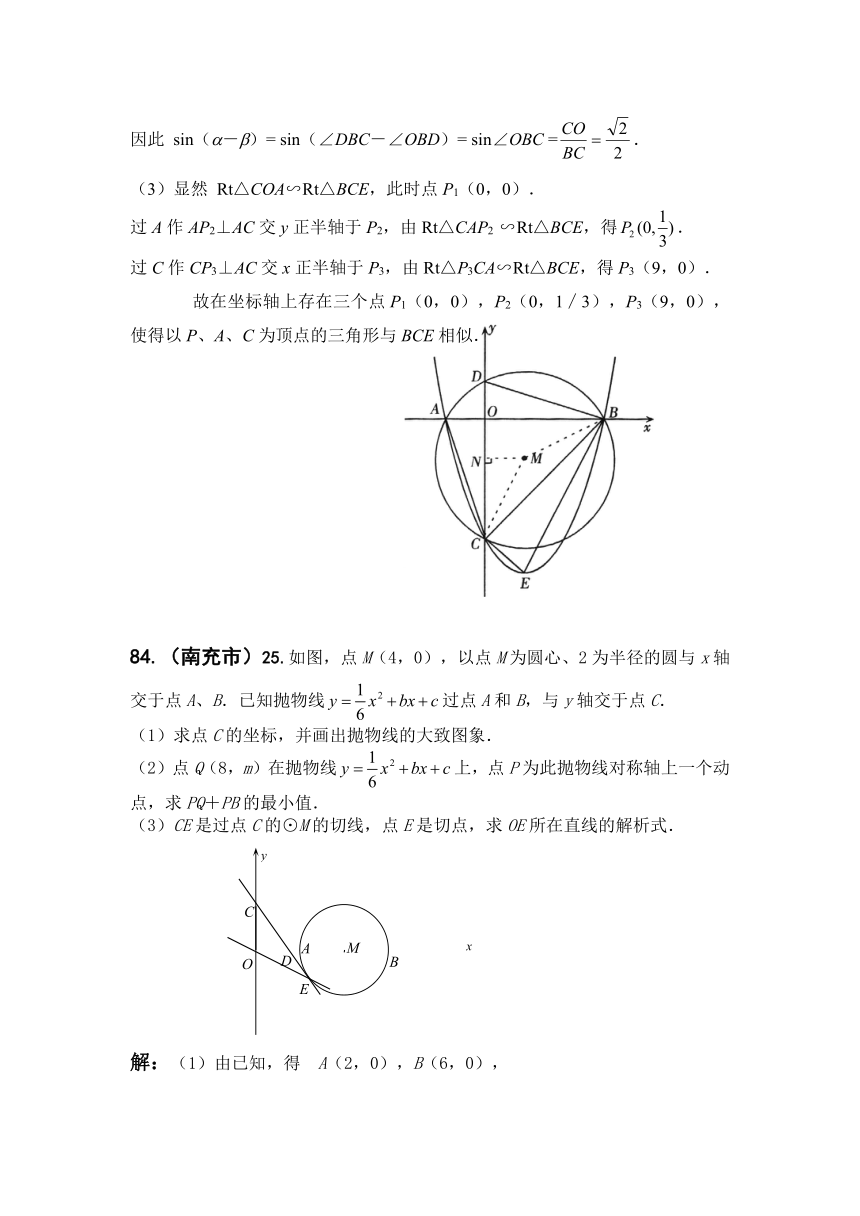
83.(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为.设⊙M与y轴交于D,抛物线的顶点为E.
(1)求m的值及抛物线的解析式;
(2)设∠DBC = ,∠CBE = ,求sin(-)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
解:(1)由题意可知C(0,-3),,
∴ 抛物线的解析式为y = ax2-2ax-3(a>0),
过M作MN⊥y轴于N,连结CM,则MN = 1,,
∴ CN = 2,于是m =-1.
同理可求得B(3,0),
∴ a×32-2-2a×3-3 = 0,得 a = 1,
∴ 抛物线的解析式为y = x2-2x-3.
(2)由(1)得 A(-1,0),E(1,-4),D(0,1).
∴ 在Rt△BCE中,,,
∴ ,,∴ ,即 ,
∴ Rt△BOD∽Rt△BCE,得 ∠CBE =∠OBD =,
因此 sin(-)= sin(∠DBC-∠OBD)= sin∠OBC =.
(3)显然 Rt△COA∽Rt△BCE,此时点P1(0,0).
过A作AP2⊥AC交y正半轴于P2,由Rt△CAP2 ∽Rt△BCE,得.
过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0).
故在坐标轴上存在三个点P1(0,0),P2(0,1∕3),P3(9,0),使得以P、A、C为顶点的三角形与BCE相似.
84.(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.
解:(1)由已知,得 A(2,0),B(6,0),
∵抛物线过点A和B,则
解得
则抛物线的解析式为.
故C(0,2).
(说明:抛物线的大致图象要过点A、B、C,其开口方向、顶点和对称轴相对准确)…(3分)
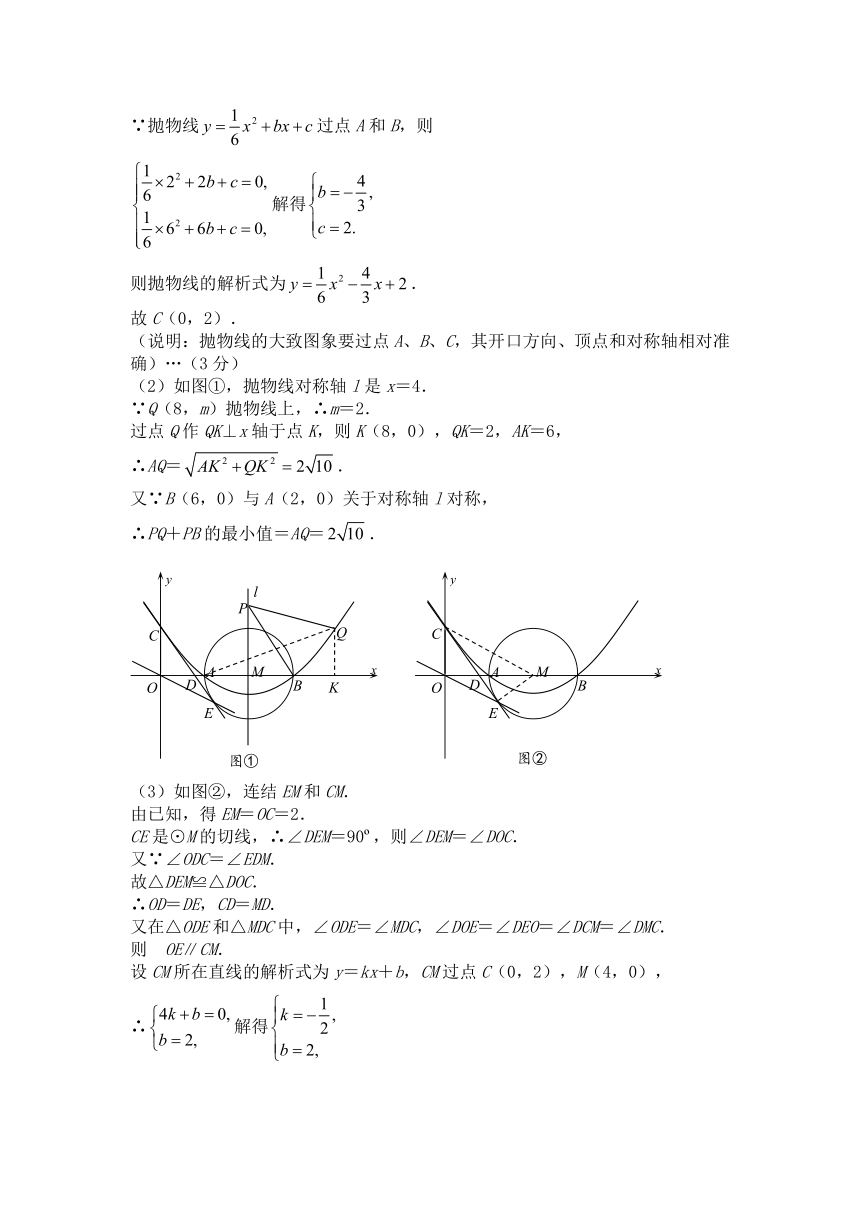
(2)如图①,抛物线对称轴l是x=4.
∵Q(8,m)抛物线上,∴m=2.
过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
∴AQ=.
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=.
(3)如图②,连结EM和CM.
由已知,得EM=OC=2.
CE是⊙M的切线,∴∠DEM=90 ,则∠DEM=∠DOC.
又∵∠ODC=∠EDM.
故△DEM≌△DOC.
∴OD=DE,CD=MD.
又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC.
则 OE∥CM.
设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0),
∴解得
直线CM的解析式为.
又∵直线OE过原点O,且OE∥CM,
则OE的解析式为y=x.
85.(内江市)25.如图(13),已知平行四边形的顶点的坐标是,平行于轴,三点在抛物线上,交轴于点,一条直线与交于点,与交于点,如果点的横坐标为,四边形的面积为.
(1)求出两点的坐标;
(2)求的值;
(3)作的内切圆,切点分别为,求的值.
解:(1)∵点A的坐标为(0,16),且AB∥x轴
∴B点纵坐标为4,且B点在抛物线上
∴点B的坐标为(10,16)
又∵点D、C在抛物线上,且CD∥x轴
∴D、C两点关于y轴对称
∴DN=CN=5.
∴D点的坐标为(-5,4)
(2)设E点的坐标为(a,16),则直线OE的解析式为:
∴F点的坐标为()
由AE=a,DF=且,得
解得a=5
(3)连结PH,PM,PK
∵⊙P是△AND的内切圆,H,M,K为切点
∴PH⊥AD,PM⊥DN,PK⊥AN
在Rt△AND中,由DN=5,AN=12,得AD=13
设⊙P的半径为r,则,r=2
在正方形PMNK中,PM=MN=2
∴
在Rt△PMF中,tan∠PMF=
86.(资阳市)25.如图10,已知抛物线P:y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x … -3 -2 1 2 …
y … - -4 - 0 …
(1) 求A、B、C三点的坐标;
(2) 若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3) 当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
解:(1)解法一:设,
任取x,y的三组值代入,求出解析式,
令y=0,求出;令x=0,得y=-4,
∴ A、B、C三点的坐标分别是A(2,0),B(-4,0),C(0,-4) .
解法二:由抛物线P过点(1,-),(-3,)可知,
抛物线P的对称轴方程为x=-1,
又∵ 抛物线P过(2,0)、(-2,-4),则由抛物线的对称性可知,
点A、B、C的坐标分别为 A(2,0),B(-4,0),C(0,-4) .
(2)由题意,,而AO=2,OC=4,AD=2-m,故DG=4-2m,
又 ,EF=DG,得BE=4-2m,∴ DE=3m,
∴SDEFG=DG·DE=(4-2m) 3m=12m-6m2 (0<m<2) .
注:也可通过解Rt△BOC及Rt△AOC,或依据△BOC是等腰直角三角形建立关系求解.
(3)∵SDEFG=12m-6m2 (0<m<2),∴m=1时,矩形的面积最大,且最大面积是6 .
当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0),
设直线DF的解析式为y=kx+b,易知,k=,b=-,∴,
又可求得抛物线P的解析式为:,
令=,可求出. 设射线DF与抛物线P相交于点N,
则N的横坐标为,过N作x轴的垂线交x轴于H,有
==,
点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是
k≠且k>0.
说明:若以上两条件错漏一个,本步不得分.
若选择另一问题:
(2)∵ HYPERLINK "http://www.1230.org" EMBED Equation.DSMT4 ,而AD=1,AO=2,OC=4,则DG=2,
又∵, 而AB=6,CP=2,OC=4,则FG=3,
∴SDEFG=DG·FG=6.
87.(自贡市)26.△ABC中,∠A,∠B,∠C的对边分别为a,b,c,抛物线y=x2-2ax+b2交x轴于两点M,N,交y轴于点P,其中M的坐标是(a+c,0).
(1)求证:△ABC是直角三角形.
(2)若S△MNP=3S△NOP,①求cosC的值;②判断△ABC的三边长能否取一组适当的值,使三角形MND(D为抛物线的顶点)是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.
解:(1)证明:∵抛物线y=x2-2ax+b2 经过点
∴
∴
∴
由勾股定理的逆定理得:
为直角三角形
(2)解:①如图所示;
∵
∴ 即
又 ∴
∴,是方程x2-2ax+b2=0的两根
∴
∴
由(1)知:在中,∠A=90°
由勾股定理得
∴
②能
由(1)知
∴顶点
过D作DE⊥x轴于点 则NE=EM DN=DM
要使为等腰直角三角形,只须ED=MN=EM
∵
∴
∴ 又c>0,∴c=1
由于c=a b=a ∴a= b=
∴当a=,b=,c=1时,为等腰直角三角形。
88.(成都市)28.在平面直角坐标系中,已知二次函数的图象与轴交于两点(点在点的左边),与轴交于点,其顶点的横坐标为1,且过点和.
(1)求此二次函数的表达式;
(2)若直线与线段交于点(不与点重合),则是否存在这样的直线,使得以为顶点的三角形与相似?若存在,求出该直线的函数表达式及点的坐标;若不存在,请说明理由;
(3)若点是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角与的大小(不必证明),并写出此时点的横坐标的取值范围.
解:(1)二次函数图象顶点的横坐标为1,且过点和,
由 解得
此二次函数的表达式为 .
(2)假设存在直线与线段交于点
(不与点重合),使得以为顶点的三角形
与相似.
在中,令,则由,
解得
.
令,得..
设过点的直线交于点,过点作轴于点.
点的坐标为,点的坐标为,点的坐标为.
.
要使或,
已有,则只需, ①
或 ②
成立.
若是①,则有.
而.
在中,由勾股定理,得.
解得 (负值舍去).
.
点的坐标为.
将点的坐标代入中,求得.
满足条件的直线的函数表达式为.
[或求出直线的函数表达式为,则与直线平行的直线的函数表达式为.此时易知,再求出直线的函数表达式为.联立求得点的坐标为.]
若是②,则有.
而.
在中,由勾股定理,得.
解得 (负值舍去).
.
点的坐标为.
将点的坐标代入中,求得.
满足条件的直线的函数表达式为.
存在直线或与线段交于点(不与点重合),使得以为顶点的三角形与相似,且点的坐标分别为或.
(3)设过点的直线与该二次函数的图象交于点.
将点的坐标代入中,求得.
此直线的函数表达式为.
设点的坐标为,并代入,
得.
解得(不合题意,舍去).
.
点的坐标为.
此时,锐角.
又二次函数的对称轴为,
点关于对称轴对称的点的坐标为.
当时,锐角;
当时,锐角;
当时,锐角.
89.(乐山市)28.如图(16),抛物线的图象与轴交于两点,与轴交于点,其中点的坐标为;直线与抛物线交于点,与轴交于点,且.
(1)用表示点的坐标;
(2)求实数的取值范围;
(3)请问的面积是否有最大值?
若有,求出这个最大值;若没有,请说明理由.
解:(1)抛物线过,
点在抛物线上,
,
点的坐标为.
(2)由(1)得,
,,.
(3)的面积有最大值,
的对称轴为,,点的坐标为,
由(1)得,
而
, 的对称轴是,
当时,取最大值,
其最大值为.
90.(巴中市)30.如图12,以边长为的正方形的对角线所在直线建立平面直角坐标系,抛物线经过点且与直线只有一个公共点.
(1)求直线的解析式.(3分)
(2)求抛物线的解析式.(3分)
(3)若点为(2)中抛物线上一点,过点作轴于点,问是否存在这样的点,使?若存在,求出点的坐标;若不存在,请说明理由.(5分)
解:(1)直线AB的解析式为:
(2)抛物线的解析式为:
(3)存在这样的点P,使△PMC∽△ADC,P点的坐标为(0,-1);(2,1);
(,);(,)。理由略。
91.(眉山市)26.如图,矩形是矩形(边在轴正半轴上,边在轴正半轴上)绕点逆时针旋转得到的,点在轴的正半轴上,点的坐标为.
(1)如果二次函数()的图象经过,两点且图象顶点的纵坐标为,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点,使得为直角三角形?若存在,请求出点的坐标和的面积;若不存在,请说明理由;
解:(1)连结,
则,
,
解得,,
所求二次函数的解析式为
(2)设存在满足题设条件的点
连结,,,过作轴于
则
,,
, 即
在二次函数的图象上
解得或
在对称轴的右支上
即是所求的点,连结,显然为等腰直角三角形.
为满足条件的点
满足条件的点是或
,
或
(3)设与的交点为
显然
在中
,即
解得,
设边所在直线的解析式为
则
解得,
所求直线解析式为
92.(内蒙古呼和浩特市) 26.如图,在矩形中,,.点在上,,交于,,交于于.点从点(不含)沿方向移动,直到使点与点重合为止.
(1)设,的面积为.
请写出关于的函数解析式,并确定的取值范围.
(2)点在运动过程中,的面积是否有最大值,若有,请求出最大值及此时的取值;若无,请说明理由.
(1)解:过点作,垂足为.
在矩形中,
又,,
又在中,
又
又在四边形中,
四边形为矩形
又
又
又
又
或
过点作,垂足为.
在中,由等积法可得
由题意可得当与重合时,与重合即,
由得即
的取值范围是
(2)面积有最大值
由(1)可得
当即时,
面积最大,即
93.(赤峰市)25. 如图,一元二次方程的二根()是抛物线与轴的两个交点的横坐标,且此抛物线过点.
(1)求此二次函数的解析式.
(2)设此抛物线的顶点为,对称轴与线段相交于点,求点和点的坐标.
(3)在轴上有一动点,当取得最小值时,求点的坐标.
解:(1)解方程
得
抛物线与轴的两个交点坐标为:
设抛物线的解析式为
在抛物线上
抛物线解析式为:
(2)由
抛物线顶点的坐标为:,对称轴方程为:
设直线的方程为:
在该直线上
解得直线的方程为:
将代入得
点坐标为
(3)作关于轴的对称点,连接;与轴交于点即为所求的点
设直线方程为
解得
直线:
令,则
点坐标为
94.(鄂尔多斯市)26. 如图17,抛物线(为常数)经过坐标原点和轴上另一点,顶点在第一象限.
(1)确定抛物线所对应的函数关系式,并写出顶点坐标;
(2)在四边形内有一矩形,点分别在上,点在轴上.当为多少时,矩形的面积最大?最大面积是多少?
解(1)抛物线过点.
顶点在第一象限,
且
抛物线
顶点坐标为
(2)①点的坐标为
②如图所示,作轴于.设点的坐标为
由抛物线的对称性可知:
当时,
时,
答:等于时,矩形的最大面积是.
95.(乌兰察布市)24. 如图所示,菱形ABCD的边长为6cm,∠DAB=60°,点M是边AD上一点,且DM=2cm,点E、F分别从A、C同时出发,以1cm/s的速度分别沿边AB、CB向点B运动,EM、CD的延长线相交于G,GF交AD于O。设运动时间为x(s),△CGF的面积为y()。
(1) 当x为何值时,GD的长度是2cm?
(2) 求y与x之间的函数关系式;
(3) 是否存在某一时刻,使得线段GF把菱形ABCD分成的上、下两部分的面积之比为1:5?若存在,求出此时x的值;若不存在,说明理由。
( http: / / blog. / user / 925 / index.html )
解:(1)∵DC∥AB
∴△DMG∽△AME
∴
∴
即当x=4s时,GD的长度是2cm
(2)∵△DMG∽△AME
∴
∴
∴GC=
过F作FH⊥DC于H点
∴FH=
∴
=
(3)设运动x(s)时,GF分菱形上、下两部分的面积比为1:5
此时△OGD∽△FGC
∴
∴
过D作DP⊥BC于P,则PD=6×sin60°=
即
解得: (舍去)
经检验:是原方程的解
∴当时,GF分菱形上、下两部分的面积比为1:5
1
2
3
4
5
5
4
3
2
1
1
2
3
5
5
4
3
2
1
C
A
M
B
x
y
O
D
E
C
A
M
B
x
y
O
D
E
Q
P
K
图①
l
C
A
M
B
x
y
O
D
E
图②
图(13)
图10
y
x
1
1
O
y
x
B
E
A
O
C
D
x
B
E
A
O
C
P
·
A
O
F
B
x
y
C
E
图(16)
图12
B
C
Q
E
D
A
P
x
y
A(3,6)
Q
C
O
B
P
x
y
A(3,6)
Q
C
O
B
P
图17
82.(四川省德阳市)25.如图,已知与轴交于点和的抛物线的顶点为,抛物线与关于轴对称,顶点为.
(1)求抛物线的函数关系式;
(2)已知原点,定点,上的点与上的点始终关于轴对称,则当点运动到何处时,以点为顶点的四边形是平行四边形?
(3)在上是否存在点,使是以为斜边且一个角为的直角三角形?若存,求出点的坐标;若不存在,说明理由.
解:(1)由题意知点的坐标为.
设的函数关系式为.
又点在抛物线上,
,解得.
抛物线的函数关系式为(或).
(2)与始终关于轴对称,
与轴平行.
设点的横坐标为,则其纵坐标为,
,,即.
当时,解得.
当时,解得.
当点运动到或或或时,
,以点为顶点的四边形是平行四边形.
(3)满足条件的点不存在.理由如下:若存在满足条件的点在上,则
,(或),
.
过点作于点,可得.
,,.
点的坐标为.
但是,当时,.
不存在这样的点构成满足条件的直角三角形.
83.(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为.设⊙M与y轴交于D,抛物线的顶点为E.
(1)求m的值及抛物线的解析式;
(2)设∠DBC = ,∠CBE = ,求sin(-)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
解:(1)由题意可知C(0,-3),,
∴ 抛物线的解析式为y = ax2-2ax-3(a>0),
过M作MN⊥y轴于N,连结CM,则MN = 1,,
∴ CN = 2,于是m =-1.
同理可求得B(3,0),
∴ a×32-2-2a×3-3 = 0,得 a = 1,
∴ 抛物线的解析式为y = x2-2x-3.
(2)由(1)得 A(-1,0),E(1,-4),D(0,1).
∴ 在Rt△BCE中,,,
∴ ,,∴ ,即 ,
∴ Rt△BOD∽Rt△BCE,得 ∠CBE =∠OBD =,
因此 sin(-)= sin(∠DBC-∠OBD)= sin∠OBC =.
(3)显然 Rt△COA∽Rt△BCE,此时点P1(0,0).
过A作AP2⊥AC交y正半轴于P2,由Rt△CAP2 ∽Rt△BCE,得.
过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0).
故在坐标轴上存在三个点P1(0,0),P2(0,1∕3),P3(9,0),使得以P、A、C为顶点的三角形与BCE相似.
84.(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.
解:(1)由已知,得 A(2,0),B(6,0),
∵抛物线过点A和B,则
解得
则抛物线的解析式为.
故C(0,2).
(说明:抛物线的大致图象要过点A、B、C,其开口方向、顶点和对称轴相对准确)…(3分)
(2)如图①,抛物线对称轴l是x=4.
∵Q(8,m)抛物线上,∴m=2.
过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
∴AQ=.
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=.
(3)如图②,连结EM和CM.
由已知,得EM=OC=2.
CE是⊙M的切线,∴∠DEM=90 ,则∠DEM=∠DOC.
又∵∠ODC=∠EDM.
故△DEM≌△DOC.
∴OD=DE,CD=MD.
又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC.
则 OE∥CM.
设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0),
∴解得
直线CM的解析式为.
又∵直线OE过原点O,且OE∥CM,
则OE的解析式为y=x.
85.(内江市)25.如图(13),已知平行四边形的顶点的坐标是,平行于轴,三点在抛物线上,交轴于点,一条直线与交于点,与交于点,如果点的横坐标为,四边形的面积为.
(1)求出两点的坐标;
(2)求的值;
(3)作的内切圆,切点分别为,求的值.
解:(1)∵点A的坐标为(0,16),且AB∥x轴
∴B点纵坐标为4,且B点在抛物线上
∴点B的坐标为(10,16)
又∵点D、C在抛物线上,且CD∥x轴
∴D、C两点关于y轴对称
∴DN=CN=5.
∴D点的坐标为(-5,4)
(2)设E点的坐标为(a,16),则直线OE的解析式为:
∴F点的坐标为()
由AE=a,DF=且,得
解得a=5
(3)连结PH,PM,PK
∵⊙P是△AND的内切圆,H,M,K为切点
∴PH⊥AD,PM⊥DN,PK⊥AN
在Rt△AND中,由DN=5,AN=12,得AD=13
设⊙P的半径为r,则,r=2
在正方形PMNK中,PM=MN=2
∴
在Rt△PMF中,tan∠PMF=
86.(资阳市)25.如图10,已知抛物线P:y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x … -3 -2 1 2 …
y … - -4 - 0 …
(1) 求A、B、C三点的坐标;
(2) 若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3) 当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
解:(1)解法一:设,
任取x,y的三组值代入,求出解析式,
令y=0,求出;令x=0,得y=-4,
∴ A、B、C三点的坐标分别是A(2,0),B(-4,0),C(0,-4) .
解法二:由抛物线P过点(1,-),(-3,)可知,
抛物线P的对称轴方程为x=-1,
又∵ 抛物线P过(2,0)、(-2,-4),则由抛物线的对称性可知,
点A、B、C的坐标分别为 A(2,0),B(-4,0),C(0,-4) .
(2)由题意,,而AO=2,OC=4,AD=2-m,故DG=4-2m,
又 ,EF=DG,得BE=4-2m,∴ DE=3m,
∴SDEFG=DG·DE=(4-2m) 3m=12m-6m2 (0<m<2) .
注:也可通过解Rt△BOC及Rt△AOC,或依据△BOC是等腰直角三角形建立关系求解.
(3)∵SDEFG=12m-6m2 (0<m<2),∴m=1时,矩形的面积最大,且最大面积是6 .
当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0),
设直线DF的解析式为y=kx+b,易知,k=,b=-,∴,
又可求得抛物线P的解析式为:,
令=,可求出. 设射线DF与抛物线P相交于点N,
则N的横坐标为,过N作x轴的垂线交x轴于H,有
==,
点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是
k≠且k>0.
说明:若以上两条件错漏一个,本步不得分.
若选择另一问题:
(2)∵ HYPERLINK "http://www.1230.org" EMBED Equation.DSMT4 ,而AD=1,AO=2,OC=4,则DG=2,
又∵, 而AB=6,CP=2,OC=4,则FG=3,
∴SDEFG=DG·FG=6.
87.(自贡市)26.△ABC中,∠A,∠B,∠C的对边分别为a,b,c,抛物线y=x2-2ax+b2交x轴于两点M,N,交y轴于点P,其中M的坐标是(a+c,0).
(1)求证:△ABC是直角三角形.
(2)若S△MNP=3S△NOP,①求cosC的值;②判断△ABC的三边长能否取一组适当的值,使三角形MND(D为抛物线的顶点)是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.
解:(1)证明:∵抛物线y=x2-2ax+b2 经过点
∴
∴
∴
由勾股定理的逆定理得:
为直角三角形
(2)解:①如图所示;
∵
∴ 即
又 ∴
∴,是方程x2-2ax+b2=0的两根
∴
∴
由(1)知:在中,∠A=90°
由勾股定理得
∴
②能
由(1)知
∴顶点
过D作DE⊥x轴于点 则NE=EM DN=DM
要使为等腰直角三角形,只须ED=MN=EM
∵
∴
∴ 又c>0,∴c=1
由于c=a b=a ∴a= b=
∴当a=,b=,c=1时,为等腰直角三角形。
88.(成都市)28.在平面直角坐标系中,已知二次函数的图象与轴交于两点(点在点的左边),与轴交于点,其顶点的横坐标为1,且过点和.
(1)求此二次函数的表达式;
(2)若直线与线段交于点(不与点重合),则是否存在这样的直线,使得以为顶点的三角形与相似?若存在,求出该直线的函数表达式及点的坐标;若不存在,请说明理由;
(3)若点是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角与的大小(不必证明),并写出此时点的横坐标的取值范围.
解:(1)二次函数图象顶点的横坐标为1,且过点和,
由 解得
此二次函数的表达式为 .
(2)假设存在直线与线段交于点
(不与点重合),使得以为顶点的三角形
与相似.
在中,令,则由,
解得
.
令,得..
设过点的直线交于点,过点作轴于点.
点的坐标为,点的坐标为,点的坐标为.
.
要使或,
已有,则只需, ①
或 ②
成立.
若是①,则有.
而.
在中,由勾股定理,得.
解得 (负值舍去).
.
点的坐标为.
将点的坐标代入中,求得.
满足条件的直线的函数表达式为.
[或求出直线的函数表达式为,则与直线平行的直线的函数表达式为.此时易知,再求出直线的函数表达式为.联立求得点的坐标为.]
若是②,则有.
而.
在中,由勾股定理,得.
解得 (负值舍去).
.
点的坐标为.
将点的坐标代入中,求得.
满足条件的直线的函数表达式为.
存在直线或与线段交于点(不与点重合),使得以为顶点的三角形与相似,且点的坐标分别为或.
(3)设过点的直线与该二次函数的图象交于点.
将点的坐标代入中,求得.
此直线的函数表达式为.
设点的坐标为,并代入,
得.
解得(不合题意,舍去).
.
点的坐标为.
此时,锐角.
又二次函数的对称轴为,
点关于对称轴对称的点的坐标为.
当时,锐角;
当时,锐角;
当时,锐角.
89.(乐山市)28.如图(16),抛物线的图象与轴交于两点,与轴交于点,其中点的坐标为;直线与抛物线交于点,与轴交于点,且.
(1)用表示点的坐标;
(2)求实数的取值范围;
(3)请问的面积是否有最大值?
若有,求出这个最大值;若没有,请说明理由.
解:(1)抛物线过,
点在抛物线上,
,
点的坐标为.
(2)由(1)得,
,,.
(3)的面积有最大值,
的对称轴为,,点的坐标为,
由(1)得,
而
, 的对称轴是,
当时,取最大值,
其最大值为.
90.(巴中市)30.如图12,以边长为的正方形的对角线所在直线建立平面直角坐标系,抛物线经过点且与直线只有一个公共点.
(1)求直线的解析式.(3分)
(2)求抛物线的解析式.(3分)
(3)若点为(2)中抛物线上一点,过点作轴于点,问是否存在这样的点,使?若存在,求出点的坐标;若不存在,请说明理由.(5分)
解:(1)直线AB的解析式为:
(2)抛物线的解析式为:
(3)存在这样的点P,使△PMC∽△ADC,P点的坐标为(0,-1);(2,1);
(,);(,)。理由略。
91.(眉山市)26.如图,矩形是矩形(边在轴正半轴上,边在轴正半轴上)绕点逆时针旋转得到的,点在轴的正半轴上,点的坐标为.
(1)如果二次函数()的图象经过,两点且图象顶点的纵坐标为,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点,使得为直角三角形?若存在,请求出点的坐标和的面积;若不存在,请说明理由;
解:(1)连结,
则,
,
解得,,
所求二次函数的解析式为
(2)设存在满足题设条件的点
连结,,,过作轴于
则
,,
, 即
在二次函数的图象上
解得或
在对称轴的右支上
即是所求的点,连结,显然为等腰直角三角形.
为满足条件的点
满足条件的点是或
,
或
(3)设与的交点为
显然
在中
,即
解得,
设边所在直线的解析式为
则
解得,
所求直线解析式为
92.(内蒙古呼和浩特市) 26.如图,在矩形中,,.点在上,,交于,,交于于.点从点(不含)沿方向移动,直到使点与点重合为止.
(1)设,的面积为.
请写出关于的函数解析式,并确定的取值范围.
(2)点在运动过程中,的面积是否有最大值,若有,请求出最大值及此时的取值;若无,请说明理由.
(1)解:过点作,垂足为.
在矩形中,
又,,
又在中,
又
又在四边形中,
四边形为矩形
又
又
又
又
或
过点作,垂足为.
在中,由等积法可得
由题意可得当与重合时,与重合即,
由得即
的取值范围是
(2)面积有最大值
由(1)可得
当即时,
面积最大,即
93.(赤峰市)25. 如图,一元二次方程的二根()是抛物线与轴的两个交点的横坐标,且此抛物线过点.
(1)求此二次函数的解析式.
(2)设此抛物线的顶点为,对称轴与线段相交于点,求点和点的坐标.
(3)在轴上有一动点,当取得最小值时,求点的坐标.
解:(1)解方程
得
抛物线与轴的两个交点坐标为:
设抛物线的解析式为
在抛物线上
抛物线解析式为:
(2)由
抛物线顶点的坐标为:,对称轴方程为:
设直线的方程为:
在该直线上
解得直线的方程为:
将代入得
点坐标为
(3)作关于轴的对称点,连接;与轴交于点即为所求的点
设直线方程为
解得
直线:
令,则
点坐标为
94.(鄂尔多斯市)26. 如图17,抛物线(为常数)经过坐标原点和轴上另一点,顶点在第一象限.
(1)确定抛物线所对应的函数关系式,并写出顶点坐标;
(2)在四边形内有一矩形,点分别在上,点在轴上.当为多少时,矩形的面积最大?最大面积是多少?
解(1)抛物线过点.
顶点在第一象限,
且
抛物线
顶点坐标为
(2)①点的坐标为
②如图所示,作轴于.设点的坐标为
由抛物线的对称性可知:
当时,
时,
答:等于时,矩形的最大面积是.
95.(乌兰察布市)24. 如图所示,菱形ABCD的边长为6cm,∠DAB=60°,点M是边AD上一点,且DM=2cm,点E、F分别从A、C同时出发,以1cm/s的速度分别沿边AB、CB向点B运动,EM、CD的延长线相交于G,GF交AD于O。设运动时间为x(s),△CGF的面积为y()。
(1) 当x为何值时,GD的长度是2cm?
(2) 求y与x之间的函数关系式;
(3) 是否存在某一时刻,使得线段GF把菱形ABCD分成的上、下两部分的面积之比为1:5?若存在,求出此时x的值;若不存在,说明理由。
( http: / / blog. / user / 925 / index.html )
解:(1)∵DC∥AB
∴△DMG∽△AME
∴
∴
即当x=4s时,GD的长度是2cm
(2)∵△DMG∽△AME
∴
∴
∴GC=
过F作FH⊥DC于H点
∴FH=
∴
=
(3)设运动x(s)时,GF分菱形上、下两部分的面积比为1:5
此时△OGD∽△FGC
∴
∴
过D作DP⊥BC于P,则PD=6×sin60°=
即
解得: (舍去)
经检验:是原方程的解
∴当时,GF分菱形上、下两部分的面积比为1:5
1
2
3
4
5
5
4
3
2
1
1
2
3
5
5
4
3
2
1
C
A
M
B
x
y
O
D
E
C
A
M
B
x
y
O
D
E
Q
P
K
图①
l
C
A
M
B
x
y
O
D
E
图②
图(13)
图10
y
x
1
1
O
y
x
B
E
A
O
C
D
x
B
E
A
O
C
P
·
A
O
F
B
x
y
C
E
图(16)
图12
B
C
Q
E
D
A
P
x
y
A(3,6)
Q
C
O
B
P
x
y
A(3,6)
Q
C
O
B
P
图17
同课章节目录
