14.2.3 三边分别相等的两个三角形 课件 (共26张PPT)数学沪科版八年级上册
文档属性
| 名称 | 14.2.3 三边分别相等的两个三角形 课件 (共26张PPT)数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 22:54:11 | ||
图片预览




文档简介
(共26张PPT)
第 14 章 全等三角形
14.2 三角形全等的判定
第 3 课时 三边分别相等的两个三角形
拿三根火柴棍搭三角形,你能搭出几种呢?试试看.
只能搭出唯一三角形
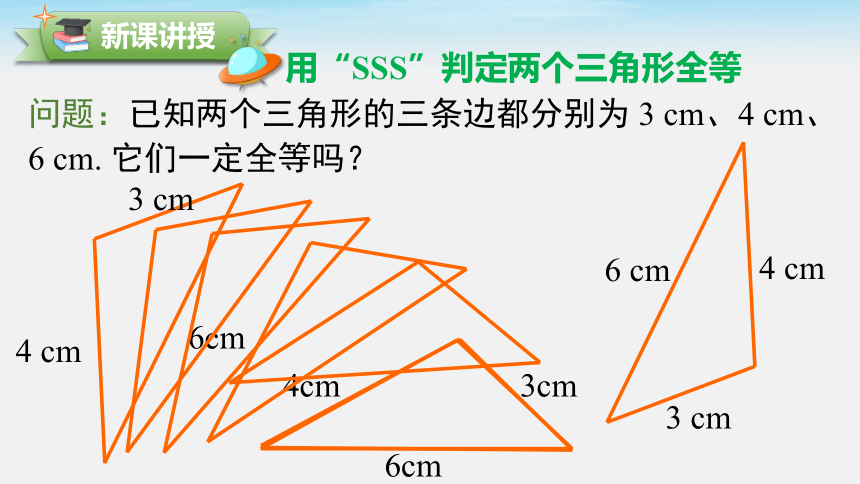
问题:已知两个三角形的三条边都分别为 3 cm、4 cm、6 cm. 它们一定全等吗?
3cm
4cm
6cm
4 cm
6cm
3 cm
6 cm
4 cm
3 cm
用“SSS”判定两个三角形全等
先任意画出一个△ABC,再画出一个△A′B′C′,使 A′B′ = AB ,B′C′ = BC,A′C′ = AC. 把画好的△A′B′C′ 剪下,放到△ABC 上,它们能重合吗?
A
B
C
A′
B′
C′
想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
作图:(1) 画 B′C′ = BC;
(2) 分别以 B',C' 为圆心,线段 AB,AC 长为半径画弧,两弧相交于点 A';
(3) 连接 A'B',A'C'.
动手试一试
点击图中按钮进行演示
文字语言:三边分别相等的两个三角形全等,
简记为“边边边”或“SSS”.
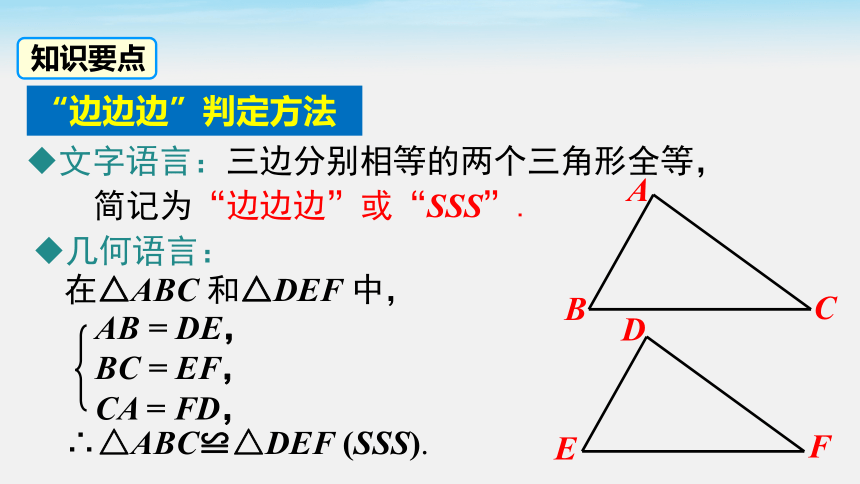
知识要点
“边边边”判定方法
A
B
C
D
E
F
几何语言:
在△ABC 和△DEF 中,
∴△ABC≌△DEF (SSS).
AB = DE,
BC = EF,
CA = FD,
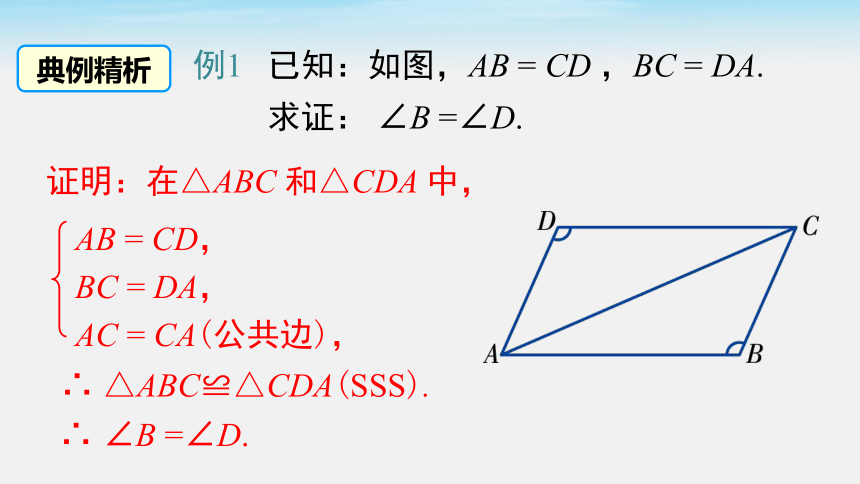
例1 已知:如图,AB = CD ,BC = DA.
求证: ∠B =∠D.
证明:在△ABC 和△CDA 中,
∴ △ABC≌△CDA(SSS).
AB = CD,
BC = DA,
AC = CA(公共边),
∴ ∠B =∠D.
典例精析
例2 已知:如图,在△ABC 中,AB = AC,点 D,E
在 BC 上,且 AD = AE,BE = CD.
求证:△ABD ≌△ACE.
证明:∵BE = CD,
∴BE - DE = CD - DE,即 BD = CE.
在△ABD 和△ACE 中,
∴△ABD≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
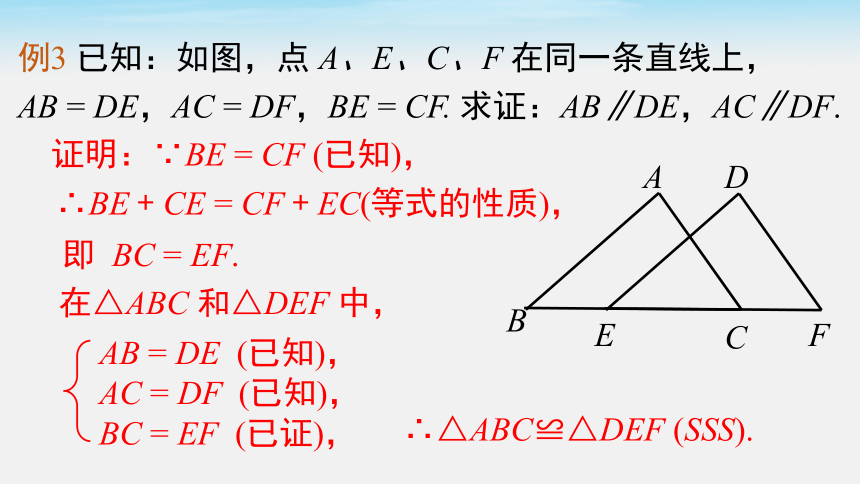
例3 已知:如图,点 A、E、C、F 在同一条直线上,
AB = DE,AC = DF,BE = CF. 求证:AB∥DE,AC∥DF.
证明:∵BE = CF (已知),
∴BE + CE = CF + EC(等式的性质),
即 BC = EF.
在△ABC 和△DEF 中,
∴△ABC≌△DEF (SSS).
AB = DE (已知),
AC = DF (已知),
BC = EF (已证),
A
D
B
E
C
F
如图,C 是 BF 的中点,AB = DC,AC = DF.
求证:△ABC≌△DCF.
在△ABC 和△DCF 中,
AB = DC
∴△ABC≌△DCF (SSS).
(已知),
(已证),
AC = DF
BC = CF
证明:∵ C 是 BF 中点,
∴ BC = CF.
(已知),
针对训练
已知:如图,点 B、E、C、F 在同一直线上,AB = DE,AC = DF,BE = CF.
求证:(1)△ABC≌△DEF;
(2)∠A =∠D.
∴△ABC≌△DEF (SSS).
在△ABC 和△DEF 中,
AB = DE,
AC = DF,
BC = EF,
证明:(1)∵ BE = CF,
即 BC = EF.
∴ BE + EC = CF + CE,
(2) ∵△ABC≌△DEF (已证),
∴∠A =∠D (全等三角形对应角相等).
变式题
(1)将三根木条用钉子钉成一个三角形木架,然后扭动它,你能发现什么?
实验探究
(2)将四根木条用钉子钉成一个四边形木架,然后扭动它,你能发现什么?
三角形的稳定性
(3)在四边形木架上再钉上一根木条,将它的一对顶点连接起来,然后再扭动它,看看有什么变化?
四边形木架会变形,但三角形的木架能固定住.
只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质的叫做三角形的稳定性.
你能说出它的原理吗?
SSS
比一比,谁知道的多
你能举出一些现实生活中的应用了三角形稳定性的例子吗
观察上面这些图片,你发现了什么?
讨论
这说明三角形有它所独有的性质.我们通过实验来探讨三角形的特性吧!
发现这些物体都用到了三角形.
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
练一练
1.下列图形中哪些具有稳定性.
2.如图,工人师傅砌门时,常用木条 EF 固定门框ABCD,使其不变形,这种做法的根据是( )
A. 两点之间线段最短
B. 三角形两边之和大于第三边
C. 长方形的四个角都是直角
D. 三角形的稳定性
D
B
A
E
F
C
D
1. 如图,D、F 是线段 BC 上的两点,AB = CE,AF = DE,
要使△ABF≌△ECD,还需要条件 (填一个条
件即可).
BF = CD
A
E
=
=
×
×
B
D
F
C
2. 如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;
③△ABD ≌△CDB;④ BA∥DC.
正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C
O
A
B
C
D
=
=
×
×
3. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了 ( )
A. 节省材料,节约成本
B. 保持对称
C. 利用三角形的稳定性
D. 美观漂亮
C
AC = FE (已知),
BC = DE (已知),
AB = FD (已证),
∴△ABC≌△FDE (SSS).
4. 已知:如图 ,AC = FE,AD = FB,BC = DE.
求证:(1)△ABC≌△FDE; (2) ∠C = ∠E.
证明:(1) ∵ AD = FB,
∴ AB = FD (等式的性质).
在△ABC 和△FDE 中,
A
C
E
D
B
F
=
=
√
√
(2) ∵△ABC≌△FDE(已证),
∴∠C =∠E (全等三角形的对应角相等).
5. 如图,AD=BC,AC=BD. 求证:∠C=∠D.
(提示:连接 AB)
证明:连接 A、B 两点.
∴△ABD≌△BAC (SSS).
AD = BC,
BD = AC,
AB = BA,
在△ABD 和△BAC 中,
∴∠D =∠C.
A
D
B
O
C
思维拓展
6. 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
△ABD≌△ACD (SSS)
AB = AC,
BD = CD,
AD = AD,
△ABH≌△ACH (SSS)
AB = AC,
BH = CH,
AH = AH,
△BDH≌△CDH (SSS)
BH = CH,
BD = CD,
DH = DH,
三边分别相等的两个三角形
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
三角形的稳定性:三角形三边长度确定了,这个三角形的形状和大小就完全确定了.
第 14 章 全等三角形
14.2 三角形全等的判定
第 3 课时 三边分别相等的两个三角形
拿三根火柴棍搭三角形,你能搭出几种呢?试试看.
只能搭出唯一三角形
问题:已知两个三角形的三条边都分别为 3 cm、4 cm、6 cm. 它们一定全等吗?
3cm
4cm
6cm
4 cm
6cm
3 cm
6 cm
4 cm
3 cm
用“SSS”判定两个三角形全等
先任意画出一个△ABC,再画出一个△A′B′C′,使 A′B′ = AB ,B′C′ = BC,A′C′ = AC. 把画好的△A′B′C′ 剪下,放到△ABC 上,它们能重合吗?
A
B
C
A′
B′
C′
想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
作图:(1) 画 B′C′ = BC;
(2) 分别以 B',C' 为圆心,线段 AB,AC 长为半径画弧,两弧相交于点 A';
(3) 连接 A'B',A'C'.
动手试一试
点击图中按钮进行演示
文字语言:三边分别相等的两个三角形全等,
简记为“边边边”或“SSS”.
知识要点
“边边边”判定方法
A
B
C
D
E
F
几何语言:
在△ABC 和△DEF 中,
∴△ABC≌△DEF (SSS).
AB = DE,
BC = EF,
CA = FD,
例1 已知:如图,AB = CD ,BC = DA.
求证: ∠B =∠D.
证明:在△ABC 和△CDA 中,
∴ △ABC≌△CDA(SSS).
AB = CD,
BC = DA,
AC = CA(公共边),
∴ ∠B =∠D.
典例精析
例2 已知:如图,在△ABC 中,AB = AC,点 D,E
在 BC 上,且 AD = AE,BE = CD.
求证:△ABD ≌△ACE.
证明:∵BE = CD,
∴BE - DE = CD - DE,即 BD = CE.
在△ABD 和△ACE 中,
∴△ABD≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
例3 已知:如图,点 A、E、C、F 在同一条直线上,
AB = DE,AC = DF,BE = CF. 求证:AB∥DE,AC∥DF.
证明:∵BE = CF (已知),
∴BE + CE = CF + EC(等式的性质),
即 BC = EF.
在△ABC 和△DEF 中,
∴△ABC≌△DEF (SSS).
AB = DE (已知),
AC = DF (已知),
BC = EF (已证),
A
D
B
E
C
F
如图,C 是 BF 的中点,AB = DC,AC = DF.
求证:△ABC≌△DCF.
在△ABC 和△DCF 中,
AB = DC
∴△ABC≌△DCF (SSS).
(已知),
(已证),
AC = DF
BC = CF
证明:∵ C 是 BF 中点,
∴ BC = CF.
(已知),
针对训练
已知:如图,点 B、E、C、F 在同一直线上,AB = DE,AC = DF,BE = CF.
求证:(1)△ABC≌△DEF;
(2)∠A =∠D.
∴△ABC≌△DEF (SSS).
在△ABC 和△DEF 中,
AB = DE,
AC = DF,
BC = EF,
证明:(1)∵ BE = CF,
即 BC = EF.
∴ BE + EC = CF + CE,
(2) ∵△ABC≌△DEF (已证),
∴∠A =∠D (全等三角形对应角相等).
变式题
(1)将三根木条用钉子钉成一个三角形木架,然后扭动它,你能发现什么?
实验探究
(2)将四根木条用钉子钉成一个四边形木架,然后扭动它,你能发现什么?
三角形的稳定性
(3)在四边形木架上再钉上一根木条,将它的一对顶点连接起来,然后再扭动它,看看有什么变化?
四边形木架会变形,但三角形的木架能固定住.
只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质的叫做三角形的稳定性.
你能说出它的原理吗?
SSS
比一比,谁知道的多
你能举出一些现实生活中的应用了三角形稳定性的例子吗
观察上面这些图片,你发现了什么?
讨论
这说明三角形有它所独有的性质.我们通过实验来探讨三角形的特性吧!
发现这些物体都用到了三角形.
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
练一练
1.下列图形中哪些具有稳定性.
2.如图,工人师傅砌门时,常用木条 EF 固定门框ABCD,使其不变形,这种做法的根据是( )
A. 两点之间线段最短
B. 三角形两边之和大于第三边
C. 长方形的四个角都是直角
D. 三角形的稳定性
D
B
A
E
F
C
D
1. 如图,D、F 是线段 BC 上的两点,AB = CE,AF = DE,
要使△ABF≌△ECD,还需要条件 (填一个条
件即可).
BF = CD
A
E
=
=
×
×
B
D
F
C
2. 如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;
③△ABD ≌△CDB;④ BA∥DC.
正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
C
O
A
B
C
D
=
=
×
×
3. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了 ( )
A. 节省材料,节约成本
B. 保持对称
C. 利用三角形的稳定性
D. 美观漂亮
C
AC = FE (已知),
BC = DE (已知),
AB = FD (已证),
∴△ABC≌△FDE (SSS).
4. 已知:如图 ,AC = FE,AD = FB,BC = DE.
求证:(1)△ABC≌△FDE; (2) ∠C = ∠E.
证明:(1) ∵ AD = FB,
∴ AB = FD (等式的性质).
在△ABC 和△FDE 中,
A
C
E
D
B
F
=
=
√
√
(2) ∵△ABC≌△FDE(已证),
∴∠C =∠E (全等三角形的对应角相等).
5. 如图,AD=BC,AC=BD. 求证:∠C=∠D.
(提示:连接 AB)
证明:连接 A、B 两点.
∴△ABD≌△BAC (SSS).
AD = BC,
BD = AC,
AB = BA,
在△ABD 和△BAC 中,
∴∠D =∠C.
A
D
B
O
C
思维拓展
6. 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
△ABD≌△ACD (SSS)
AB = AC,
BD = CD,
AD = AD,
△ABH≌△ACH (SSS)
AB = AC,
BH = CH,
AH = AH,
△BDH≌△CDH (SSS)
BH = CH,
BD = CD,
DH = DH,
三边分别相等的两个三角形
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
三角形的稳定性:三角形三边长度确定了,这个三角形的形状和大小就完全确定了.
