22.3实际问题与二次函数同步训练(无答案) 人教版数学九年级上册
文档属性
| 名称 | 22.3实际问题与二次函数同步训练(无答案) 人教版数学九年级上册 | 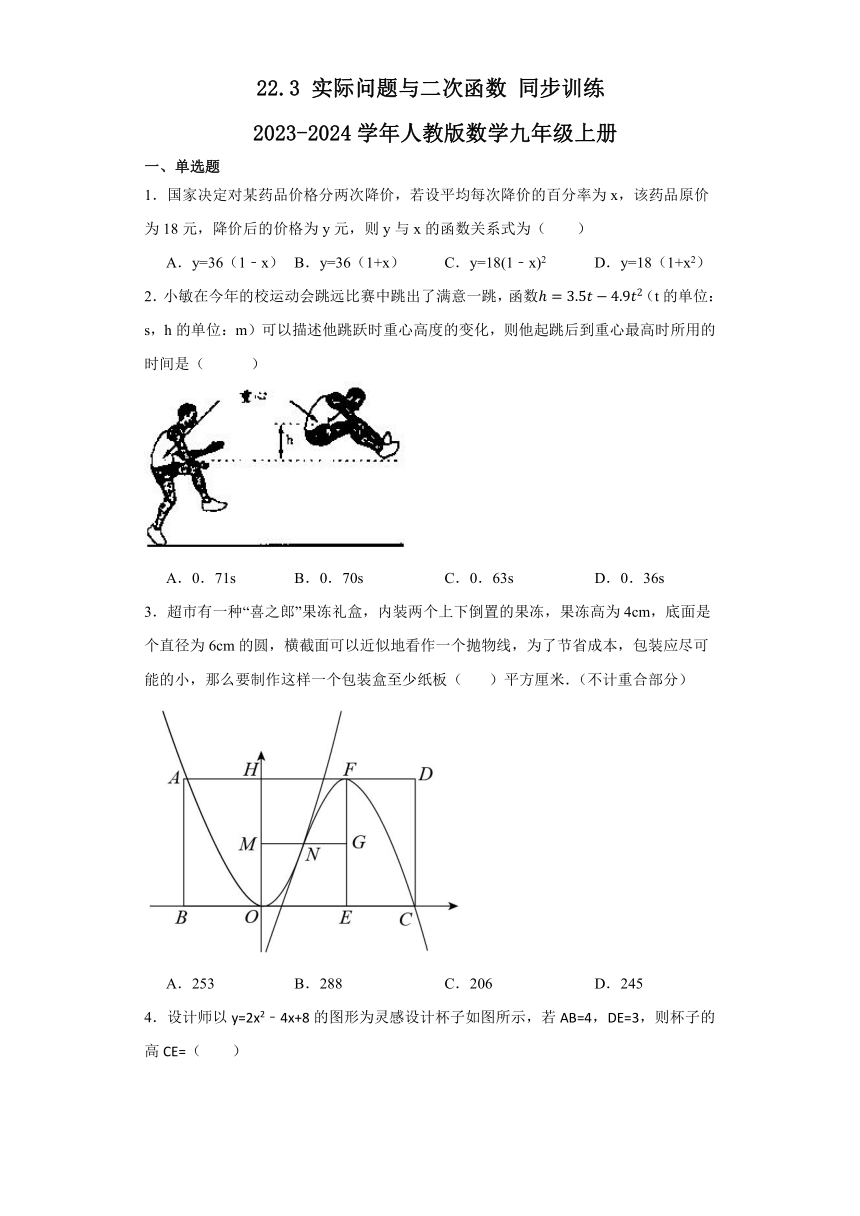 | |
| 格式 | docx | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 09:56:34 | ||
图片预览


文档简介
22.3 实际问题与二次函数 同步训练
2023-2024学年人教版数学九年级上册
一、单选题
1.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y与x的函数关系式为( )
A.y=36(1﹣x) B.y=36(1+x) C.y=18(1﹣x)2 D.y=18(1+x2)
2.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
3.超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)
A.253 B.288 C.206 D.245
4.设计师以y=2x2﹣4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )
A.17 B.11 C.8 D.7
5.在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
A.1月份 B.2月份
C.5月份 D.7月份
6.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD最大面积是( )
A.60 m2 B.63 m2 C.64 m2 D.66 m2
7.三角形的一边长与这边上的高都为xcm,其面积是ycm2 , 则y与x的函数关系为( )
A.y=x2 B.y=2x2
C.y= x2 D.y= x2
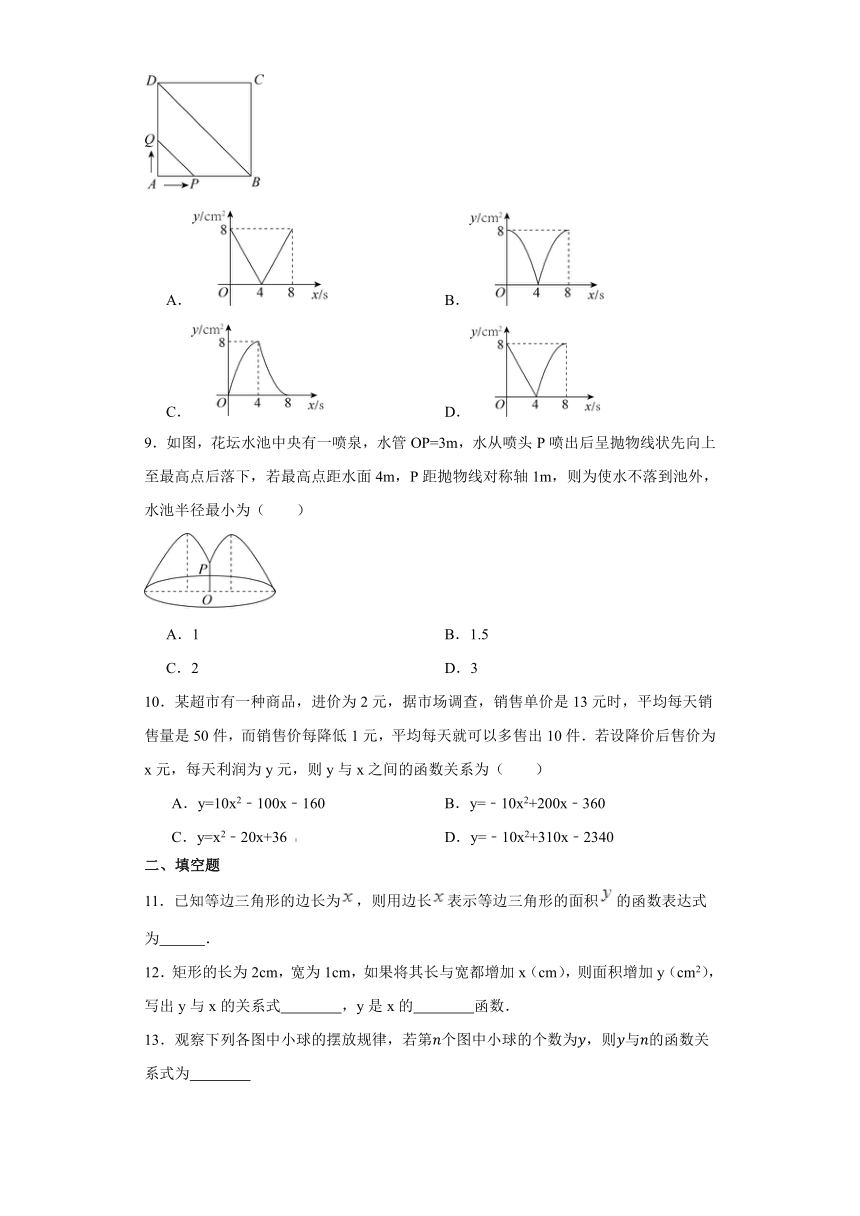
8.如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为
A. B.
C. D.
9.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B.1.5
C.2 D.3
10.某超市有一种商品,进价为2元,据市场调查,销售单价是13元时,平均每天销售量是50件,而销售价每降低1元,平均每天就可以多售出10件.若设降价后售价为x元,每天利润为y元,则y与x之间的函数关系为( )
A.y=10x2﹣100x﹣160 B.y=﹣10x2+200x﹣360
C.y=x2﹣20x+36 D.y=﹣10x2+310x﹣2340
二、填空题
11.已知等边三角形的边长为,则用边长表示等边三角形的面积的函数表达式为 .
12.矩形的长为2cm,宽为1cm,如果将其长与宽都增加x(cm),则面积增加y(cm2),写出y与x的关系式 ,y是x的 函数.
13.观察下列各图中小球的摆放规律,若第个图中小球的个数为,则与的函数关系式为
14.两个正方形的周长之和为20cm,其中一个正方形的边长是xcm,则这两个正方形的面积之和y(cm2)与x(cm)的函数关系式为 .
15.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ -4 -2 0 1 4
植物高度增长量l/mm 41 49 49 46 25
科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为 ℃.
16.拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是
三、解答题
17.如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从点B开始沿边BC向点C以4mm/s的速度移动.如果P,Q两点分别从A,B两点同时出发,请求出△PBQ的面积S与出发时间t的函数解析式及t的取值范围.
18.东门天虹商场购进一批“童乐”牌玩具,每件成本价30元,每件玩具销售单价x(元)与每天的销售量y(件)的关系如下表:
若每天的销售量y(件)是销售单价x(元)的一次函数
(1)求y与x的函数关系式;
(2)设东门天虹商场销售“童乐”牌儿童玩具每天获得的利润为w(元),当销售单价x为何值时,每天可获得最大利润?此时最大利润是多少?
(3)若东门天虹商场销售“童乐”牌玩具每天获得的利润最多不超过15000元,最低不低于12000元,那么商场该如何确定“童乐”牌玩具的销售单价的波动范围?请你直接给出销售单价x的范围.
19.如图,抛物线交x轴的正半轴于点A,点B(,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n= .(直接写出答案)
20.如图,抛物线与x轴交于点A(﹣, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
2023-2024学年人教版数学九年级上册
一、单选题
1.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y与x的函数关系式为( )
A.y=36(1﹣x) B.y=36(1+x) C.y=18(1﹣x)2 D.y=18(1+x2)
2.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
3.超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)
A.253 B.288 C.206 D.245
4.设计师以y=2x2﹣4x+8的图形为灵感设计杯子如图所示,若AB=4,DE=3,则杯子的高CE=( )
A.17 B.11 C.8 D.7
5.在1~7月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
A.1月份 B.2月份
C.5月份 D.7月份
6.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD最大面积是( )
A.60 m2 B.63 m2 C.64 m2 D.66 m2
7.三角形的一边长与这边上的高都为xcm,其面积是ycm2 , 则y与x的函数关系为( )
A.y=x2 B.y=2x2
C.y= x2 D.y= x2
8.如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为
A. B.
C. D.
9.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B.1.5
C.2 D.3
10.某超市有一种商品,进价为2元,据市场调查,销售单价是13元时,平均每天销售量是50件,而销售价每降低1元,平均每天就可以多售出10件.若设降价后售价为x元,每天利润为y元,则y与x之间的函数关系为( )
A.y=10x2﹣100x﹣160 B.y=﹣10x2+200x﹣360
C.y=x2﹣20x+36 D.y=﹣10x2+310x﹣2340
二、填空题
11.已知等边三角形的边长为,则用边长表示等边三角形的面积的函数表达式为 .
12.矩形的长为2cm,宽为1cm,如果将其长与宽都增加x(cm),则面积增加y(cm2),写出y与x的关系式 ,y是x的 函数.
13.观察下列各图中小球的摆放规律,若第个图中小球的个数为,则与的函数关系式为
14.两个正方形的周长之和为20cm,其中一个正方形的边长是xcm,则这两个正方形的面积之和y(cm2)与x(cm)的函数关系式为 .
15.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ -4 -2 0 1 4
植物高度增长量l/mm 41 49 49 46 25
科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为 ℃.
16.拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是
三、解答题
17.如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从点B开始沿边BC向点C以4mm/s的速度移动.如果P,Q两点分别从A,B两点同时出发,请求出△PBQ的面积S与出发时间t的函数解析式及t的取值范围.
18.东门天虹商场购进一批“童乐”牌玩具,每件成本价30元,每件玩具销售单价x(元)与每天的销售量y(件)的关系如下表:
若每天的销售量y(件)是销售单价x(元)的一次函数
(1)求y与x的函数关系式;
(2)设东门天虹商场销售“童乐”牌儿童玩具每天获得的利润为w(元),当销售单价x为何值时,每天可获得最大利润?此时最大利润是多少?
(3)若东门天虹商场销售“童乐”牌玩具每天获得的利润最多不超过15000元,最低不低于12000元,那么商场该如何确定“童乐”牌玩具的销售单价的波动范围?请你直接给出销售单价x的范围.
19.如图,抛物线交x轴的正半轴于点A,点B(,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n= .(直接写出答案)
20.如图,抛物线与x轴交于点A(﹣, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
同课章节目录
