京教版八年级数学第十六章四边形整章水平测试(B)
文档属性
| 名称 | 京教版八年级数学第十六章四边形整章水平测试(B) |

|
|
| 格式 | rar | ||
| 文件大小 | 69.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-16 00:00:00 | ||
图片预览

文档简介
第十六章四边形整章水平测试(B)
一、试试你的身手(每小题3分,共24分)
1.矩形的对角线相交所成的钝角为120°,短边为3.6cm,则对角线长为 .
2.一个平行四边形的周长为24cm,两邻边之比为2∶1,则它的各边长为 .
3.如果四边形ABCD是 ,则它的对角线AC与BD互相垂直平分(只需填写一组你认为合适的条件).
4.顺次连接四边形各边的中点所得的四边形为 ,顺次连接对角线相等的四边形各边的中点所得的四边形是 ,顺次连接对角线互相垂直的四边形各边的中点所得的四边形是 ,顺次连接对角线既相等又垂直的四边形各边的中点所得的四边形是 .
5.若正方形的对角线长为a,那么它的对角线的交点到它的边的距离为 .
6.如图1,菱形ABCD中,若∠ABC=120°,则BD∶AC= .
7.如图2,矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠,点D落在E处,且CE与AB交于F,那么AF的长是 .
8.等腰梯形ABCD中,AD∥BC,(1)如果延长BA和CD相交于E,则EA= ;(2)如果作AF∥DC交BC于F,则△ABF是 三角形,四边形ADCF是 形;(3)如果作AG⊥BC于G,DH⊥BC于H,则BG= = ;(4)如果作DK∥AC交BC的延长线于K,则DK= = .
二、相信你的选择(每小题3分,共24分)
1.顺次连接下列各图形的中点,构成的图形一定是正方形的为( )
A.平行四边形 B.矩形
C.菱形 D.对角线互相垂直的等腰梯形
2.在矩形ABCD中,AC、BD相交于O,OF⊥AB于F,若AC=2AD,OF=9cm,则BD的长为( )
A.90cm B.36cm C.93cm D.183cm
3.如图3,EF过对角线的交点O,并交AD于E,交BC于F.若AB=4,BC=5,OE=1.5,则EFCD的周长是( )
A.16 B.14 C.12 D.10
4.梯形的两底长分别为16cm和8cm,两底角分别为60°和30°,则较短的腰长为( )
A.8cm B.6cm C.1cm D.4cm
5.等腰梯形两底之差等于一腰长,它的腰与下底的夹角是( )
A.15° B.30° C.45° D.60°
6.若平面上A、B两点到直线l的距离分别为m,n(m>n),则线段AB的中点到l的距离为( )
A. B. C. D.或
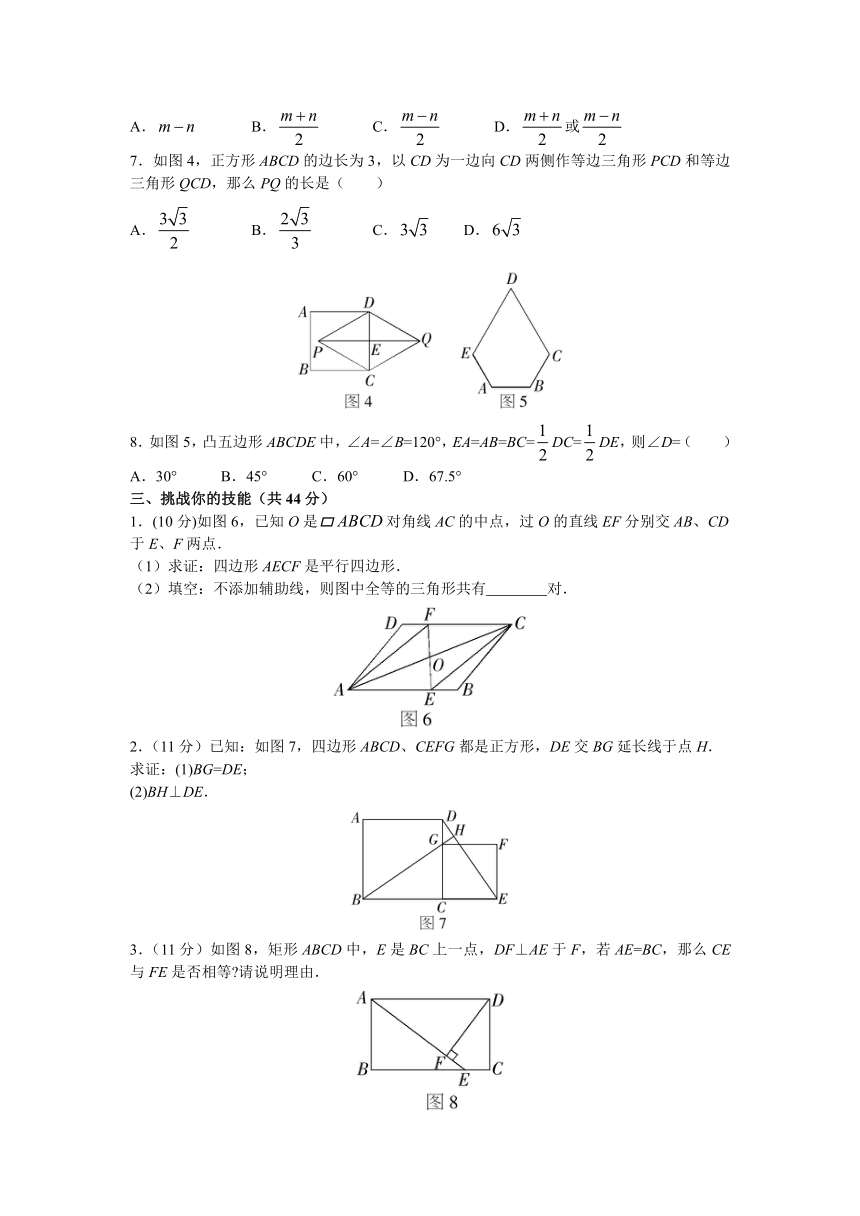
7.如图4,正方形ABCD的边长为3,以CD为一边向CD两侧作等边三角形PCD和等边三角形QCD,那么PQ的长是( )
A. B. C. D.
8.如图5,凸五边形ABCDE中,∠A=∠B=120°,EA=AB=BC=DC=DE,则∠D=( )
A.30° B.45° C.60° D.67.5°
三、挑战你的技能(共44分)
1.(10分)如图6,已知O是对角线AC的中点,过O的直线EF分别交AB、CD于E、F两点.
(1)求证:四边形AECF是平行四边形.
(2)填空:不添加辅助线,则图中全等的三角形共有 对.
2.(11分)已知:如图7,四边形ABCD、CEFG都是正方形,DE交BG延长线于点H.
求证:(1)BG=DE;
(2)BH⊥DE.
3.(11分)如图8,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC,那么CE与FE是否相等 请说明理由.
4.(12分)如图9,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E,点F在DE的延长线上,且AF=CE.
求证:四边形ACEF是菱形.
四、拓广探索(共28分)
1.(14分)在正方形ABCD所在的平面内有一点P,使△PAB、△PBC、△PCD、△PDA都是等腰三角形,具有这样性质的点共有多少个?试画图说明.
2.(14分)如图10,梯形ABCD中,AB∥DC,AD=DC=CB,AD、BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F.
(1)请写出图中4组相等的线段(已知的相等线段除外);
(2)选择(1)中你所写的一组相等线段,说明它们相等的理由.
参考答案:
一、1.7.2cm 2.8cm,4cm ,8cm,4cm 3.正方形(答案不惟一)
4.平行四边形,菱形,矩形,正方形 5. 6.
7. 8.,等腰,平行四边,,,,
二、1~4.DBCD 5~8.DDCC
三、1.(1)证明略.(2)6
2.证明略.
3..理由略.
4.证明略.
四、1.共9个,图略
2.(1),,,,(答案不惟一).
(2)证明略.
PAGE
一、试试你的身手(每小题3分,共24分)
1.矩形的对角线相交所成的钝角为120°,短边为3.6cm,则对角线长为 .
2.一个平行四边形的周长为24cm,两邻边之比为2∶1,则它的各边长为 .
3.如果四边形ABCD是 ,则它的对角线AC与BD互相垂直平分(只需填写一组你认为合适的条件).
4.顺次连接四边形各边的中点所得的四边形为 ,顺次连接对角线相等的四边形各边的中点所得的四边形是 ,顺次连接对角线互相垂直的四边形各边的中点所得的四边形是 ,顺次连接对角线既相等又垂直的四边形各边的中点所得的四边形是 .
5.若正方形的对角线长为a,那么它的对角线的交点到它的边的距离为 .
6.如图1,菱形ABCD中,若∠ABC=120°,则BD∶AC= .
7.如图2,矩形ABCD中,AB=8,BC=6,将矩形沿AC折叠,点D落在E处,且CE与AB交于F,那么AF的长是 .
8.等腰梯形ABCD中,AD∥BC,(1)如果延长BA和CD相交于E,则EA= ;(2)如果作AF∥DC交BC于F,则△ABF是 三角形,四边形ADCF是 形;(3)如果作AG⊥BC于G,DH⊥BC于H,则BG= = ;(4)如果作DK∥AC交BC的延长线于K,则DK= = .
二、相信你的选择(每小题3分,共24分)
1.顺次连接下列各图形的中点,构成的图形一定是正方形的为( )
A.平行四边形 B.矩形
C.菱形 D.对角线互相垂直的等腰梯形
2.在矩形ABCD中,AC、BD相交于O,OF⊥AB于F,若AC=2AD,OF=9cm,则BD的长为( )
A.90cm B.36cm C.93cm D.183cm
3.如图3,EF过对角线的交点O,并交AD于E,交BC于F.若AB=4,BC=5,OE=1.5,则EFCD的周长是( )
A.16 B.14 C.12 D.10
4.梯形的两底长分别为16cm和8cm,两底角分别为60°和30°,则较短的腰长为( )
A.8cm B.6cm C.1cm D.4cm
5.等腰梯形两底之差等于一腰长,它的腰与下底的夹角是( )
A.15° B.30° C.45° D.60°
6.若平面上A、B两点到直线l的距离分别为m,n(m>n),则线段AB的中点到l的距离为( )
A. B. C. D.或
7.如图4,正方形ABCD的边长为3,以CD为一边向CD两侧作等边三角形PCD和等边三角形QCD,那么PQ的长是( )
A. B. C. D.
8.如图5,凸五边形ABCDE中,∠A=∠B=120°,EA=AB=BC=DC=DE,则∠D=( )
A.30° B.45° C.60° D.67.5°
三、挑战你的技能(共44分)
1.(10分)如图6,已知O是对角线AC的中点,过O的直线EF分别交AB、CD于E、F两点.
(1)求证:四边形AECF是平行四边形.
(2)填空:不添加辅助线,则图中全等的三角形共有 对.
2.(11分)已知:如图7,四边形ABCD、CEFG都是正方形,DE交BG延长线于点H.
求证:(1)BG=DE;
(2)BH⊥DE.
3.(11分)如图8,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC,那么CE与FE是否相等 请说明理由.
4.(12分)如图9,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E,点F在DE的延长线上,且AF=CE.
求证:四边形ACEF是菱形.
四、拓广探索(共28分)
1.(14分)在正方形ABCD所在的平面内有一点P,使△PAB、△PBC、△PCD、△PDA都是等腰三角形,具有这样性质的点共有多少个?试画图说明.
2.(14分)如图10,梯形ABCD中,AB∥DC,AD=DC=CB,AD、BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F.
(1)请写出图中4组相等的线段(已知的相等线段除外);
(2)选择(1)中你所写的一组相等线段,说明它们相等的理由.
参考答案:
一、1.7.2cm 2.8cm,4cm ,8cm,4cm 3.正方形(答案不惟一)
4.平行四边形,菱形,矩形,正方形 5. 6.
7. 8.,等腰,平行四边,,,,
二、1~4.DBCD 5~8.DDCC
三、1.(1)证明略.(2)6
2.证明略.
3..理由略.
4.证明略.
四、1.共9个,图略
2.(1),,,,(答案不惟一).
(2)证明略.
PAGE
同课章节目录
