18.1.2勾股定理的应用
文档属性
| 名称 | 18.1.2勾股定理的应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 653.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-17 00:00:00 | ||
图片预览




文档简介
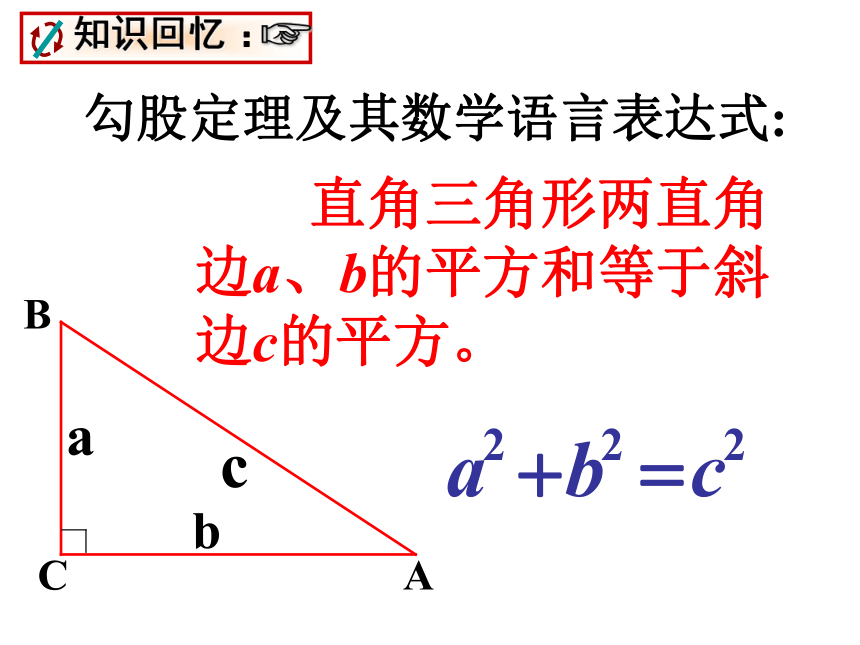
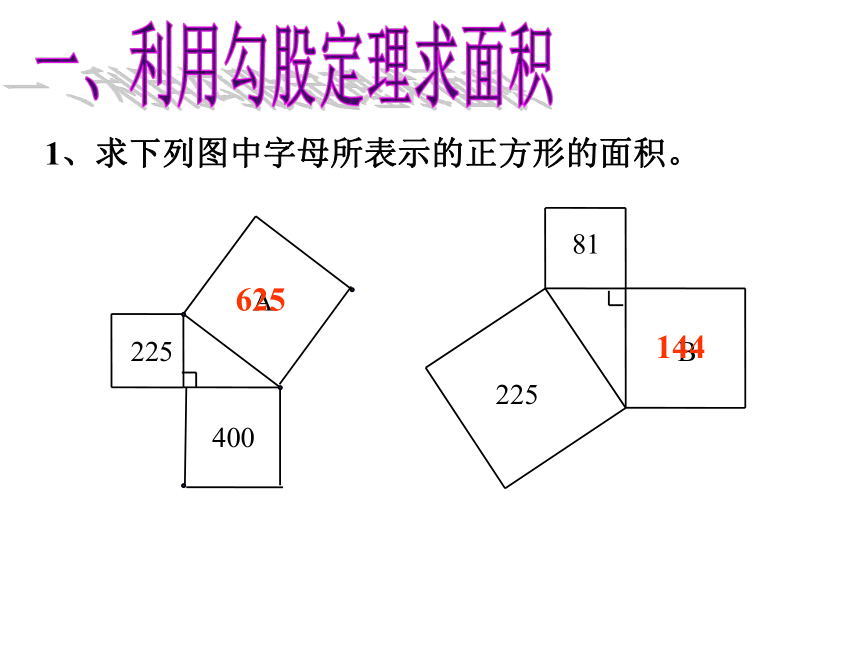
课件22张PPT。18.1.2 勾 股 定 理的应用勾股定理及其数学语言表达式: 直角三角形两直角边a、b的平方和等于斜边c的平方。CAB1、求下列图中字母所表示的正方形的面积。625144一、利用勾股定理求面积
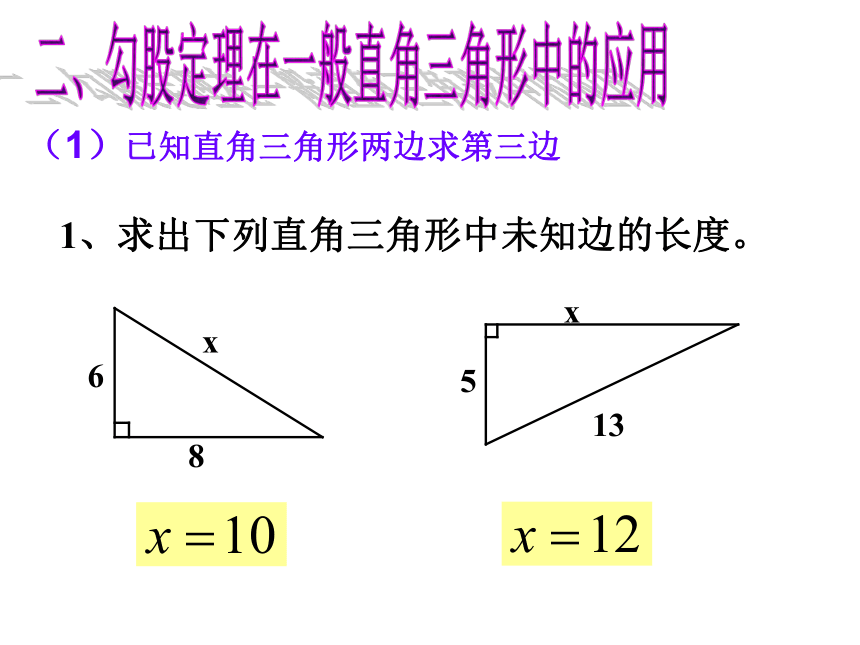
(1)已知直角三角形两边求第三边1、求出下列直角三角形中未知边的长度。二、勾股定理在一般直角三角形中的应用2、在直角△ABC中,∠C=90°,a=5,b=12,则c=_______。
3、在,∠B=90°,a=3,b=4,则c=_______。
4、在直角△ABC中,其中a=3,b=4,则c=______。
5、直角三角形一直角边长为6㎝,斜边为10㎝,则这个三角形的面积为_______,斜边上的高为_________6、若一直角三角形的两条直角边分别为3cm和4cm,则斜边长为_______,斜边上的高为_________。136、在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕b=3﹕4,c=15.求a、b.分析:通过设未知数,根据勾股定理列出方程求出a、b.解:设a=3x,b=4x
∵在Rt△ABC中,∠C=90°,
∴由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.
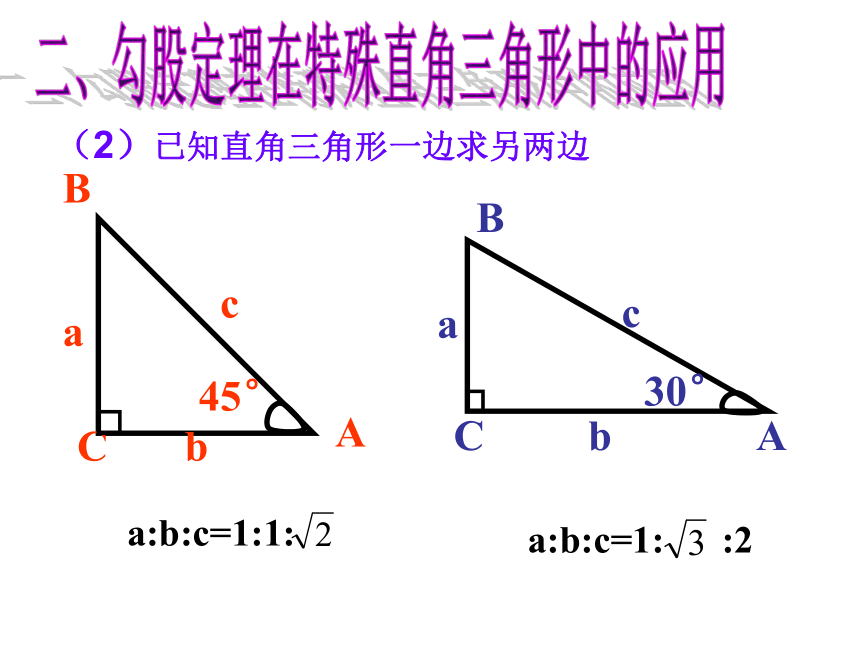
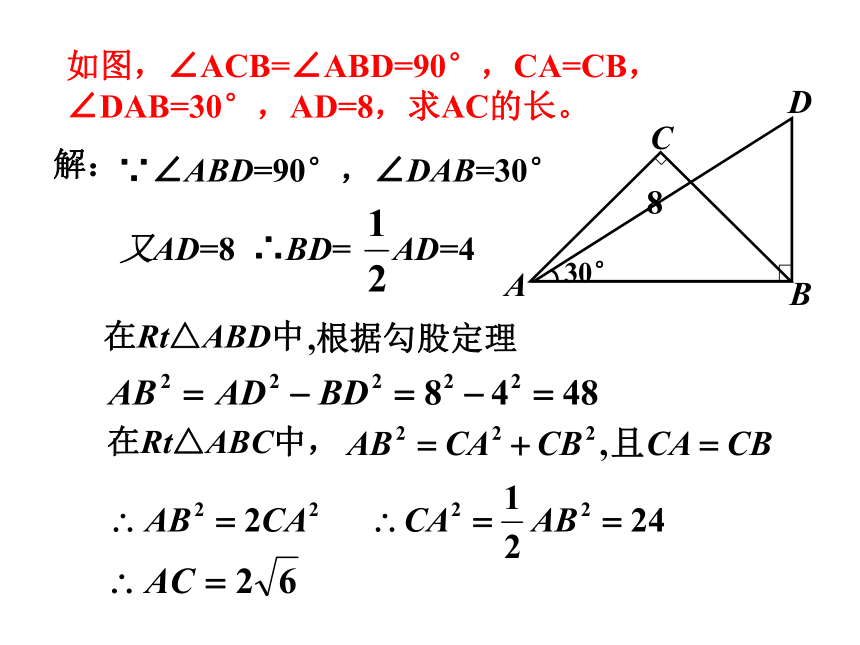
(2)已知直角三角形一边求另两边 a:b:c=1:1: a:b:c=1: :2二、勾股定理在特殊直角三角形中的应用如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米三、勾股定理在实际生活中的应用1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
1、如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
34“路”ABC542、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。笨人执竿要进屋,无奈门框拦住竿,
横多四尺竖多二,没法急得放声哭.
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足.
借问竿长多少数,谁人算出我佩服.执竿进屋读这首诗,并回答其中的问题。探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能1m 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD探究2一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD 从题目和图形中,你能得到哪些信息?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m阿满想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(x+1)米x米DABC名题鉴赏E 《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?1
(1)已知直角三角形两边求第三边1、求出下列直角三角形中未知边的长度。二、勾股定理在一般直角三角形中的应用2、在直角△ABC中,∠C=90°,a=5,b=12,则c=_______。
3、在,∠B=90°,a=3,b=4,则c=_______。
4、在直角△ABC中,其中a=3,b=4,则c=______。
5、直角三角形一直角边长为6㎝,斜边为10㎝,则这个三角形的面积为_______,斜边上的高为_________6、若一直角三角形的两条直角边分别为3cm和4cm,则斜边长为_______,斜边上的高为_________。136、在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕b=3﹕4,c=15.求a、b.分析:通过设未知数,根据勾股定理列出方程求出a、b.解:设a=3x,b=4x
∵在Rt△ABC中,∠C=90°,
∴由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.
(2)已知直角三角形一边求另两边 a:b:c=1:1: a:b:c=1: :2二、勾股定理在特殊直角三角形中的应用如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米三、勾股定理在实际生活中的应用1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
1、如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了________步路, 却踩伤了花草。 (假设1米为2步)
34“路”ABC542、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。笨人执竿要进屋,无奈门框拦住竿,
横多四尺竖多二,没法急得放声哭.
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足.
借问竿长多少数,谁人算出我佩服.执竿进屋读这首诗,并回答其中的问题。探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能1m 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD探究2一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?探究2 ACOBD 从题目和图形中,你能得到哪些信息?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m阿满想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(x+1)米x米DABC名题鉴赏E 《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?1
