冀教版六年级上册数学-4.3 探索圆的面积公式课件 (共13张PPT)
文档属性
| 名称 | 冀教版六年级上册数学-4.3 探索圆的面积公式课件 (共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 278.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 10:39:30 | ||
图片预览





文档简介
(共13张PPT)
《探索圆的面积公式》
学习目标:
1.利用转化的数学思想,探索圆的面积的计算公式的过程。
2.掌握圆的面积的计算公式。能够利用公式进行简单的面积计算。
3.继续培养分析、观察和概括的能力。
1.我们研究过哪些平面图形的面积?它们的计算公式各是什么?
一、复习导入
长方形: 长×宽
正方形: 边长×边长
平行四边形: 底×高
三角形: 底×高÷2
梯形: (上底+下底)×高÷2
2.想一想:我们是如何研究平行四边形面积的?
转化思想
圆形草坪的直径为20米,每平方米8元,铺满草皮需要多少钱?
二、探究新知
活动提示:
①试着将平均分成若干等份的圆形纸片通过剪一剪、拼一拼的方式,转化成已学过的图形。
②每小组中只需1人记录操作过程。
③观察拼出的图形和原来的圆,存在什么样的等量关系。
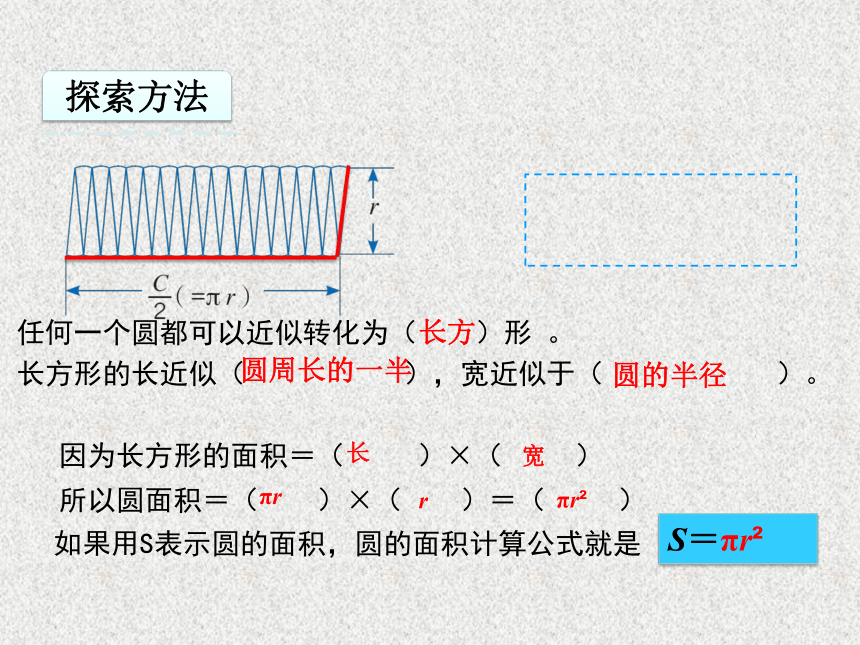
任何一个圆都可以近似转化为( )形 。
长方形的长近似( ),宽近似于( )。
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
如果用S表示圆的面积,圆的面积计算公式就是
长方
圆的半径
长
宽
πr
r
πr
S=πr
绿色圃中小学教育网http://www.lspjy.com
探索方法
圆周长的一半
20÷2=10(m)
3.14×102 =314(m2)
314×8= (元)
答:铺满草皮需要 元。
2512
2512
二、探究新知
圆形草坪的直径为20m,每平方米草皮8元。铺满草皮需要多少钱?
例1
1.计算下面圆的面积:
r=2cm
d=6cm
.
.
三、巩固新知
2.判断对错:
圆的半径越大,圆所占的面积越大。( )
半径是2厘米的圆,它的周长和面积相等。( )
圆的半径扩大3倍,它的面积扩大6倍。( )
√
×
×
三、巩固新知
一只羊拴在木桩上,绳长5m,它能吃到草的面积有多大?
四、巩固练习
三、巩固新知
四、课堂小结
谈谈你的收获?
刘徽“割圆术”
3世纪中期,我国魏晋时期的数学家刘徽首创割圆术。
所谓“割圆术”,是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法。刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。
作业:
用两根10米长的铁丝分别围成圆和正方形,谁的面积大?
再见
《探索圆的面积公式》
学习目标:
1.利用转化的数学思想,探索圆的面积的计算公式的过程。
2.掌握圆的面积的计算公式。能够利用公式进行简单的面积计算。
3.继续培养分析、观察和概括的能力。
1.我们研究过哪些平面图形的面积?它们的计算公式各是什么?
一、复习导入
长方形: 长×宽
正方形: 边长×边长
平行四边形: 底×高
三角形: 底×高÷2
梯形: (上底+下底)×高÷2
2.想一想:我们是如何研究平行四边形面积的?
转化思想
圆形草坪的直径为20米,每平方米8元,铺满草皮需要多少钱?
二、探究新知
活动提示:
①试着将平均分成若干等份的圆形纸片通过剪一剪、拼一拼的方式,转化成已学过的图形。
②每小组中只需1人记录操作过程。
③观察拼出的图形和原来的圆,存在什么样的等量关系。
任何一个圆都可以近似转化为( )形 。
长方形的长近似( ),宽近似于( )。
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
如果用S表示圆的面积,圆的面积计算公式就是
长方
圆的半径
长
宽
πr
r
πr
S=πr
绿色圃中小学教育网http://www.lspjy.com
探索方法
圆周长的一半
20÷2=10(m)
3.14×102 =314(m2)
314×8= (元)
答:铺满草皮需要 元。
2512
2512
二、探究新知
圆形草坪的直径为20m,每平方米草皮8元。铺满草皮需要多少钱?
例1
1.计算下面圆的面积:
r=2cm
d=6cm
.
.
三、巩固新知
2.判断对错:
圆的半径越大,圆所占的面积越大。( )
半径是2厘米的圆,它的周长和面积相等。( )
圆的半径扩大3倍,它的面积扩大6倍。( )
√
×
×
三、巩固新知
一只羊拴在木桩上,绳长5m,它能吃到草的面积有多大?
四、巩固练习
三、巩固新知
四、课堂小结
谈谈你的收获?
刘徽“割圆术”
3世纪中期,我国魏晋时期的数学家刘徽首创割圆术。
所谓“割圆术”,是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法。刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。
作业:
用两根10米长的铁丝分别围成圆和正方形,谁的面积大?
再见
