25.2随机事件的概率 华东师大版初中数学九年级上册同步练习(含答案解析)
文档属性
| 名称 | 25.2随机事件的概率 华东师大版初中数学九年级上册同步练习(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 432.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 11:33:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
25.2随机事件的概率华东师大版初中数学九年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.在元旦晚会上有一个闯关活动:将张分别画有正方形、圆、平行四边形、菱形的卡片任意摆放卡片大小、质地、颜色完全相同,将有图形的一面朝下,从中任意翻开张,如果翻开的张都是既是中心对称图形又是轴对称图形,就可以过关那么一次过关的概率是( )
A. B. C. D.
2.甲、乙、丙三位同学把自己的数学课本放在一起,每人从中随机抽起一本不放回,三位同学抽到的课本都是自己课本的概率是( )
A. B. C. D.
3.下列说法中,正确的是( )
A. 不可能事件发生的概率为
B. 随机事件发生的概率为
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币次,正面朝上的次数一定为次
4.从,,,,这个数中随机抽取一个数,抽到有理数的概率是( )
A. B. C. D.
5.“敬老爱老”是中华民族的优秀传统美德小刚、小强计划利用暑期从,,三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )
A. B. C. D.
6.正方形地板由块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区城的概率是( )
A.
B.
C.
D.
7.“天宫课堂”第二课月日在中国空间站开讲,包括六个项目:太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节.若随机选取一个项目写观后感,则恰好选到“实验”项目的概率是( )
A. B. C. D.
8.在一个不透明的口袋中装有个红球,个白球和若干个黑球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到白球的频率稳定在附近,则口袋中黑球可能有( )
A. 个 B. 个 C. 个 D. 个
9.育种小组对某品种小麦发芽情况进行测试,在测试条件相同的情况下,得到如下数据:
抽查小麦粒数
发芽粒数
则的值最有可能是( )
A. B. C. D.
10.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“数”,如“”就是一个“数”若十位上的数字为,则从,,,中任选两数,能与组成“数”的概率是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.在一个不透明的口袋中,装有个球,它们分别写有数字,,,这些球除上面数字外,其余都相同先将这些球摇匀后,随机摸出一球,记下数字后,放回;再摇匀,再摸出一球则摸出的两球的数字之和是的概率是______ .
12.如图,在中,,,分别是,,的中点,,,分别是,,的中点.若随机向内投一粒米,则米粒落在图中阴影部分的概率是 .
13.一个不透明的口袋里有颗球,除颜色以外完全相同,其中颗红球,颗白球,从口袋中随机摸出两颗球,则恰好摸出颗红球颗白球的概率是______.
14.足球是一项非常古老的运动,最早起源于中国,是全球体育界最具影响力的单项体育运动,现从一批足球中随机抽检部分足球的质量,统计结果如表:
抽取的足球数个
优等品的频数个
优等品的频率
据此推测,从这批足球中随机抽取一个足球是优等品的概率是______结果精确到.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
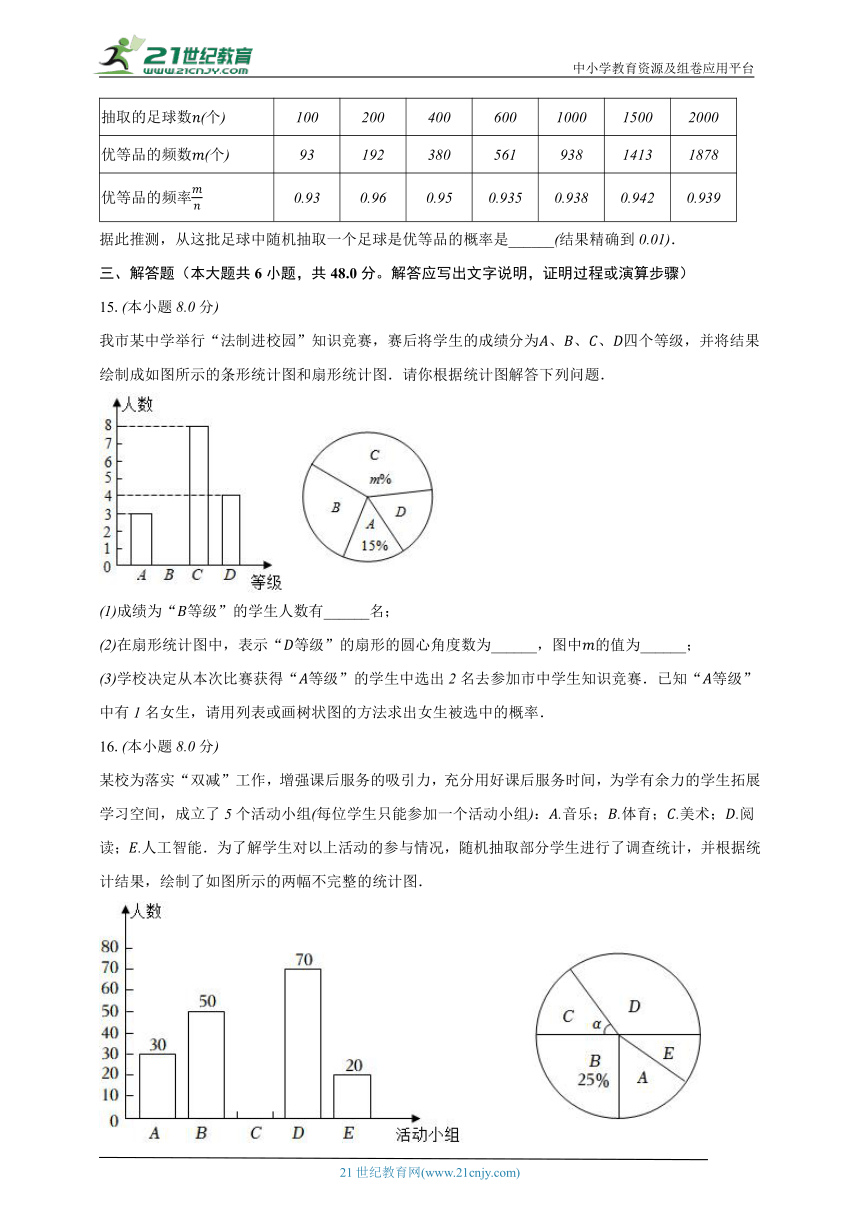
我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为、、、四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.
成绩为“等级”的学生人数有______名;
在扇形统计图中,表示“等级”的扇形的圆心角度数为______,图中的值为______;
学校决定从本次比赛获得“等级”的学生中选出名去参加市中学生知识竞赛.已知“等级”中有名女生,请用列表或画树状图的方法求出女生被选中的概率.
16.本小题分
某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了个活动小组每位学生只能参加一个活动小组:音乐;体育;美术;阅读;人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
此次调查一共随机抽取了______名学生;
补全条形统计图要求在条形图上方注明人数;
扇形统计图中圆心角______度;
若该校有名学生,估计该校参加组阅读的学生人数;
刘老师计划从组人工智能的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.
17.本小题分
一部好的纪录片可以让学生开阔眼界,建立认知,构建宏大的世界观,某中学为了丰富学生暑期生活,向学生们推荐了地球脉动、蓝色星球、冰冻星球、地球的力量这四部纪录片,为了了解学生观看这四部纪录片的情况,就“这四部纪录片你看完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
本次调查所得数据的众数是______ 部,中位数是______ 部,扇形统计图中“部”所在扇形的圆心角为______ 度;
请将条形统计图补充完整;
现有两名没有看过这四部纪录片的学生准备从这四部纪录片中各自随机选择一部来观看,请用树状图或列表法求他们选中同一部纪录片的概率.
18.本小题分
某学校到红色景区开展红色研学活动,研学活动中有一个重温石林会议召开的场景活动,该活动需要派杨老师去领取四个灯笼,灯笼上分别写有“军”“民”“一”“家”外观完全一样.
杨老师从四个灯笼中任取一个,取到写有“一”的灯笼的概率是______ .
杨老师从四个灯笼中不放回地先后取出两个灯笼,请用列表或画树状图的方法求杨老师恰好取到写有“军”“民”的两个灯笼的概率.
19.本小题分
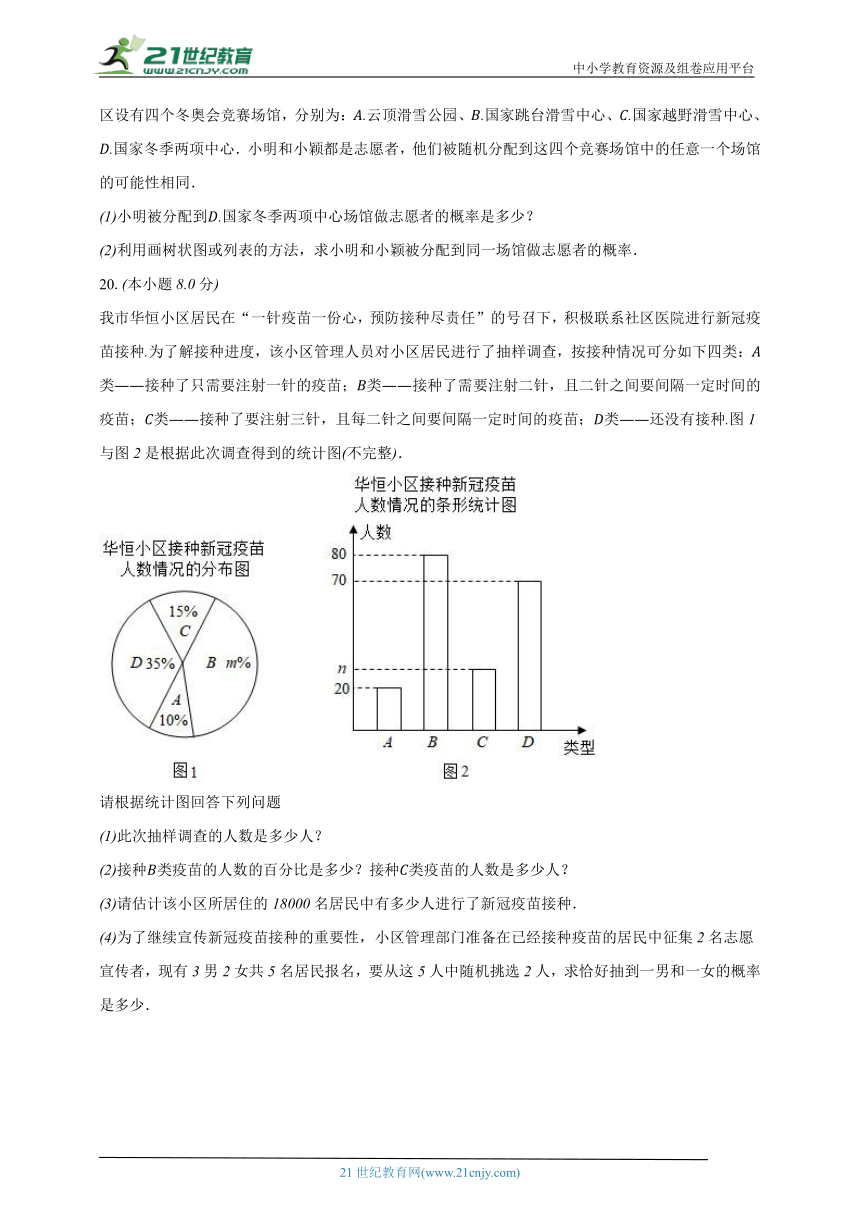
第届冬季奥林匹克运动会于年月至日在我国北京张家口成功举办,其中张家口赛区设有四个冬奥会竞赛场馆,分别为:云顶滑雪公园、国家跳台滑雪中心、国家越野滑雪中心、国家冬季两项中心.小明和小颖都是志愿者,他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同.
小明被分配到国家冬季两项中心场馆做志愿者的概率是多少?
利用画树状图或列表的方法,求小明和小颖被分配到同一场馆做志愿者的概率.
20.本小题分
我市华恒小区居民在“一针疫苗一份心,预防接种尽责任”的号召下,积极联系社区医院进行新冠疫苗接种为了解接种进度,该小区管理人员对小区居民进行了抽样调查,按接种情况可分如下四类:类接种了只需要注射一针的疫苗;类接种了需要注射二针,且二针之间要间隔一定时间的疫苗;类接种了要注射三针,且每二针之间要间隔一定时间的疫苗;类还没有接种图与图是根据此次调查得到的统计图不完整.
请根据统计图回答下列问题
此次抽样调查的人数是多少人?
接种类疫苗的人数的百分比是多少?接种类疫苗的人数是多少人?
请估计该小区所居住的名居民中有多少人进行了新冠疫苗接种.
为了继续宣传新冠疫苗接种的重要性,小区管理部门准备在已经接种疫苗的居民中征集名志愿宣传者,现有男女共名居民报名,要从这人中随机挑选人,求恰好抽到一男和一女的概率是多少.
答案和解析
1.【答案】
【解析】解:将正方形、圆、平行四边形、菱形分别记为,,,,
则既是中心对称图形又是轴对称图形的为,,,
画树状图如下:
共有种等可能的结果,其中翻开的张都是既是中心对称图形又是轴对称图形的结果有:,,,,,,共种,
一次过关的概率是.
故选:.
画树状图得出所有等可能的结果数以及翻开的张都是既是中心对称图形又是轴对称图形的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法、轴对称图形、中心对称图形,熟练掌握列表法与树状图法、轴对称图形、中心对称图形是解答本题的关键.
2.【答案】
【解析】解:设甲、乙、丙三位同学的数学课本分别记为,,,
画树状图如下:
共有种等可能的结果,其中三位同学抽到的课本都是自己课本的结果有种,
三位同学抽到的课本都是自己课本的概率是.
故选:.
画树状图得出所有等可能的结果数以及三位同学抽到的课本都是自己课本的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
3.【答案】
【解析】【分析】
本题考查了概率的意义:一般地,在大量重复实验中,如果事件发生的频率会稳定在某个常数附近,那么这个常数就叫做事件的概率,记为;概率是频率多个的波动稳定值,是对事件发生可能性大小的量的表现.必然发生的事件的概率;不可能发生事件的概率.
根据概率的意义和必然发生的事件的概率、不可能发生事件的概率对、、进行判定;根据频率与概率的区别对进行判定.
【解答】
解:不可能事件发生的概率为,所以选项正确
B.随机事件发生的概率在与之间,所以选项错误
C.概率很小的事件不是不可能发生,而是发生的可能性较小,所以选项错误
D.投掷一枚质地均匀的硬币次,正面朝上的次数可能为次,所以选项错误.
故选A.
4.【答案】
【解析】【分析】
根据有理数的定义可找出在,,,,这个数中只有、和为有理数,再根据概率公式即可求出抽到有理数的概率.
本题考查了概率公式以及有理数,根据有理数的定义找出个数中的有理数的个数是解题的关键,还考查了概率计算公式,即概率所求情况数与总情况数之比.
【解答】
解:在,,,,这个数中只有,和为有理数,
从,,,,这个数中随机抽取一个数,抽到有理数的概率是.
故选:.
5.【答案】
【解析】解:画树状图如图:
共有种等可能的结果数,其中两人恰好选择同一场所的结果数为,
明明和亮亮两人恰好选择同一场馆的概率,
故选:.
画出树状图展示所有种等可能的结果数,找出两人恰好选择同一场所的结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
6.【答案】
【解析】【分析】
本题考查几何概率.
求出黑色区域的面积与整个地板面积的比值即可解决问题.
【解答】
解:由图可知,黑色区域的地板面积合起来等于两块正方形的面积,而地板总共有块正方形,
黑色区域面积在整个地板面积中所占的比值,
米粒停在黑色区域的概率是.
7.【答案】
【解析】【分析】
本题考查概率的求法与运用,一般方法为:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
根据随机事件概率大小的求法,找准两点:
符合条件的情况数目;
全部情况的总数.
二者的比值就是其发生的概率的大小.
【解答】
解:共个项目,“实验”项目有太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验共个,
随机选取一个项目写观后感,则恰好选到“实验”项目的概率是,
故选:.
8.【答案】
【解析】【分析】
此题主要考查了利用频率估计概率,根据大量反复试验下频率稳定值即概率是解题关键.
由摸到白球的频率稳定在附近得出口袋中得到白球的概率,进而求出黑球个数即可.
【解答】
解:设黑球个数为个,
摸到白球的频率稳定在附近,
口袋中得到红色球的概率为,
,
解得:,
经检验:是原方程的根,
故黑球的个数为个.
9.【答案】
【解析】解:,
,
,
,
,
可估计某品种小麦发芽情况的概率为,
则.
故选:.
根据次测试从粒增加到粒时,测试某品种小麦发芽情况的频率趋近于,从而求得答案.
本题考查了利用频率估计概率的知识,解题的关键是了解:大量反复试验下频率稳定值即概率.用到的知识点为:频率所求情况数与总情况数之比.
10.【答案】
【解析】解:画树状图如图所示.
因为可以组成的数有,,,,,,,,,,,,且是等可能性的,其中是“数”的有,,,,,,共六个,所以从,,,中任选两数,能与组成“数”的概率是.
11.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,其中摸出的两球的数字之和是的结果有种,
摸出的两球的数字之和是的概率是,
故答案为:.
画树状图,共有种等可能的结果,其中摸出的两球的数字之和是的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件;用到的知识点为:概率所求情况数与总情况数之比.
12.【答案】
【解析】略
13.【答案】
【解析】解:画树状图如图:
共有个等可能的结果,恰好摸出颗红球颗白球的结果有个,
恰好摸出颗红球颗白球的概率为,
故答案为:.
画树状图,共有个等可能的结果,恰好摸出颗红球颗白球的结果有个,再由概率公式求解即可.
此题考查的是用列表法或树状图法求概率.用到的知识点为:概率所求情况数与总情况数之比.
14.【答案】
【解析】解:从这批足球中,任意抽取一只足球是优等品的概率的估计值是.
故答案为:.
由表中数据可判断频率在左右摆动,于是利于频率估计概率可判断任意抽取一只足球是优等品的概率为.
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
15.【答案】;
,;
“等级”男女,从中选取人,所有可能出现的结果如下:
共有种可能出现的结果,其中女生被选中的有种,
女生被选中.
【解析】【分析】
本题考查条形统计图、扇形统计图的意义和制作方法,列表法求随机事件发生的概率,列举出所有可能出现的结果是求概率的前提.
等的有人,占调查人数的,可求出调查人数,进而求出等的人数;
等级占调查人数的,因此相应的圆心角为的即可,计算等级所占的百分比,即可求出的值;
用列表法表示所有可能出现的结果,进而求出相应的概率.
【解答】
解:名,名,
故答案为:;
,,即,
故答案为:,;
见答案.
16.【答案】解:;
组的人数为:名,
补全条形统计图如下:
;
名,
答:估计该校参加组阅读的学生人数为名;
画树状图如下:
共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,
恰好抽中甲、乙两人的概率为.
【解析】解:此次调查一共随机抽取的学生人数为:名,
故答案为:;
组的人数为:名,
补全条形统计图如下:
扇形统计图中圆心角,
故答案为:;
名,
答:估计该校参加组阅读的学生人数为名;
画树状图如下:
共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,
恰好抽中甲、乙两人的概率为.
由组的人数除以所占百分比即可;
求出组的人数,补全条形统计图即可;
由乘以组所占的比例即可;
由该校共有学生人数乘以参加组阅读的学生人数所占的比例即可;
画树状图,共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率以及条形统计图和扇形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
17.【答案】
【解析】解:被调查的总人数为人,
“部”对应的人数为人,
人数最多的数部,即众数为部,
处于中间位置的两个数据都是“部”,中位数为“部”
扇形统计图中“部”所在扇形的圆心角为,
故答案为:,,;
条形统计图如图所示,
地球脉动、蓝色星球、冰冻星球、地球的力量分别用字母、、、表示,
树状图如图所示:
一共有种等可能性,其中他们恰好选中同一部纪录片的可能性有种,
故他们恰好选中同一部纪录片的概率是,
即他们恰好选中同一部纪录片的概率是;
先求出被调查的总人数,继而求出“部”对应的人数,根据众数的定义可得答案,用乘以“部”人数所占比例即可;
根据以上所求结果即可补全图形即可;
列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
本题主要考查了扇形统计图以及条形统计图的运用,读懂统计图,从统计图中得到必要的信息是解题的关键;用到的知识点为:概率所求情况数与总情况数之比.
18.【答案】
【解析】解:杨老师从四个灯笼中任取一个,取到写有“一”的灯笼的概率是,
故答案为:;
画树状图如图:
共有个等可能的结果,杨老师恰好取到写有“军”“民”的两个灯笼的结果有个,
杨老师恰好取到写有“军”“民”的两个灯笼的概率为.
直接由概率公式求解即可;
画树状图,共有个等可能的结果,杨老师恰好取到写有“军”“民”的两个灯笼的结果有个,再由概率公式求解即可.
本题考查了列表法与树状图法,用到的知识点为:概率所求情况数与总情况数之比.
19.【答案】解:小明被分配到国家冬季两项中心场馆做志愿者的概率是;
画树状图如下:
共有种等可能的结果,其中小明和小颖被分配到同一场馆做志愿者的结果有种,
小明和小颖被分配到同一场馆做志愿者的概率为.
【解析】直接由概率公式求解即可;
画树状图,共有种等可能的结果,其中小明和小颖被分配到同一场馆做志愿者的结果有种,再由概率公式求解即可.
此题考查了用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
20.【答案】解:此次抽样调查的人数为:人;
接种类疫苗的人数的百分比为:,
接种类疫苗的人数为:人;
人,
即估计该小区所居住的名居民中有人进行了新冠疫苗接种.
画树状图如图:
共有种等可能的结果,恰好抽到一男和一女的结果有种,
恰好抽到一男和一女的概率为.
【解析】由类的人数除以所占百分比即可求解;
由接种类疫苗的人数除以此次抽样调查的人数得出此次抽样调查的人数所占的百分比,再由此次抽样调查的人数乘接种类疫苗的人数所占的百分比即可;
由该小区所居住的总人数乘、、三类所占的百分比之和即可;
画树状图,共有种等可能的结果,恰好抽到一男和一女的结果有种,再由概率公式求解即可.
此题考查的是用列表法或树状图法求概率以及条形统计图和扇形统计图.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
25.2随机事件的概率华东师大版初中数学九年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.在元旦晚会上有一个闯关活动:将张分别画有正方形、圆、平行四边形、菱形的卡片任意摆放卡片大小、质地、颜色完全相同,将有图形的一面朝下,从中任意翻开张,如果翻开的张都是既是中心对称图形又是轴对称图形,就可以过关那么一次过关的概率是( )
A. B. C. D.
2.甲、乙、丙三位同学把自己的数学课本放在一起,每人从中随机抽起一本不放回,三位同学抽到的课本都是自己课本的概率是( )
A. B. C. D.
3.下列说法中,正确的是( )
A. 不可能事件发生的概率为
B. 随机事件发生的概率为
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币次,正面朝上的次数一定为次
4.从,,,,这个数中随机抽取一个数,抽到有理数的概率是( )
A. B. C. D.
5.“敬老爱老”是中华民族的优秀传统美德小刚、小强计划利用暑期从,,三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )
A. B. C. D.
6.正方形地板由块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区城的概率是( )
A.
B.
C.
D.
7.“天宫课堂”第二课月日在中国空间站开讲,包括六个项目:太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节.若随机选取一个项目写观后感,则恰好选到“实验”项目的概率是( )
A. B. C. D.
8.在一个不透明的口袋中装有个红球,个白球和若干个黑球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到白球的频率稳定在附近,则口袋中黑球可能有( )
A. 个 B. 个 C. 个 D. 个
9.育种小组对某品种小麦发芽情况进行测试,在测试条件相同的情况下,得到如下数据:
抽查小麦粒数
发芽粒数
则的值最有可能是( )
A. B. C. D.
10.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“数”,如“”就是一个“数”若十位上的数字为,则从,,,中任选两数,能与组成“数”的概率是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.在一个不透明的口袋中,装有个球,它们分别写有数字,,,这些球除上面数字外,其余都相同先将这些球摇匀后,随机摸出一球,记下数字后,放回;再摇匀,再摸出一球则摸出的两球的数字之和是的概率是______ .
12.如图,在中,,,分别是,,的中点,,,分别是,,的中点.若随机向内投一粒米,则米粒落在图中阴影部分的概率是 .
13.一个不透明的口袋里有颗球,除颜色以外完全相同,其中颗红球,颗白球,从口袋中随机摸出两颗球,则恰好摸出颗红球颗白球的概率是______.
14.足球是一项非常古老的运动,最早起源于中国,是全球体育界最具影响力的单项体育运动,现从一批足球中随机抽检部分足球的质量,统计结果如表:
抽取的足球数个
优等品的频数个
优等品的频率
据此推测,从这批足球中随机抽取一个足球是优等品的概率是______结果精确到.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为、、、四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.
成绩为“等级”的学生人数有______名;
在扇形统计图中,表示“等级”的扇形的圆心角度数为______,图中的值为______;
学校决定从本次比赛获得“等级”的学生中选出名去参加市中学生知识竞赛.已知“等级”中有名女生,请用列表或画树状图的方法求出女生被选中的概率.
16.本小题分
某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了个活动小组每位学生只能参加一个活动小组:音乐;体育;美术;阅读;人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
此次调查一共随机抽取了______名学生;
补全条形统计图要求在条形图上方注明人数;
扇形统计图中圆心角______度;
若该校有名学生,估计该校参加组阅读的学生人数;
刘老师计划从组人工智能的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.
17.本小题分
一部好的纪录片可以让学生开阔眼界,建立认知,构建宏大的世界观,某中学为了丰富学生暑期生活,向学生们推荐了地球脉动、蓝色星球、冰冻星球、地球的力量这四部纪录片,为了了解学生观看这四部纪录片的情况,就“这四部纪录片你看完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
本次调查所得数据的众数是______ 部,中位数是______ 部,扇形统计图中“部”所在扇形的圆心角为______ 度;
请将条形统计图补充完整;
现有两名没有看过这四部纪录片的学生准备从这四部纪录片中各自随机选择一部来观看,请用树状图或列表法求他们选中同一部纪录片的概率.
18.本小题分
某学校到红色景区开展红色研学活动,研学活动中有一个重温石林会议召开的场景活动,该活动需要派杨老师去领取四个灯笼,灯笼上分别写有“军”“民”“一”“家”外观完全一样.
杨老师从四个灯笼中任取一个,取到写有“一”的灯笼的概率是______ .
杨老师从四个灯笼中不放回地先后取出两个灯笼,请用列表或画树状图的方法求杨老师恰好取到写有“军”“民”的两个灯笼的概率.
19.本小题分
第届冬季奥林匹克运动会于年月至日在我国北京张家口成功举办,其中张家口赛区设有四个冬奥会竞赛场馆,分别为:云顶滑雪公园、国家跳台滑雪中心、国家越野滑雪中心、国家冬季两项中心.小明和小颖都是志愿者,他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同.
小明被分配到国家冬季两项中心场馆做志愿者的概率是多少?
利用画树状图或列表的方法,求小明和小颖被分配到同一场馆做志愿者的概率.
20.本小题分
我市华恒小区居民在“一针疫苗一份心,预防接种尽责任”的号召下,积极联系社区医院进行新冠疫苗接种为了解接种进度,该小区管理人员对小区居民进行了抽样调查,按接种情况可分如下四类:类接种了只需要注射一针的疫苗;类接种了需要注射二针,且二针之间要间隔一定时间的疫苗;类接种了要注射三针,且每二针之间要间隔一定时间的疫苗;类还没有接种图与图是根据此次调查得到的统计图不完整.
请根据统计图回答下列问题
此次抽样调查的人数是多少人?
接种类疫苗的人数的百分比是多少?接种类疫苗的人数是多少人?
请估计该小区所居住的名居民中有多少人进行了新冠疫苗接种.
为了继续宣传新冠疫苗接种的重要性,小区管理部门准备在已经接种疫苗的居民中征集名志愿宣传者,现有男女共名居民报名,要从这人中随机挑选人,求恰好抽到一男和一女的概率是多少.
答案和解析
1.【答案】
【解析】解:将正方形、圆、平行四边形、菱形分别记为,,,,
则既是中心对称图形又是轴对称图形的为,,,
画树状图如下:
共有种等可能的结果,其中翻开的张都是既是中心对称图形又是轴对称图形的结果有:,,,,,,共种,
一次过关的概率是.
故选:.
画树状图得出所有等可能的结果数以及翻开的张都是既是中心对称图形又是轴对称图形的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法、轴对称图形、中心对称图形,熟练掌握列表法与树状图法、轴对称图形、中心对称图形是解答本题的关键.
2.【答案】
【解析】解:设甲、乙、丙三位同学的数学课本分别记为,,,
画树状图如下:
共有种等可能的结果,其中三位同学抽到的课本都是自己课本的结果有种,
三位同学抽到的课本都是自己课本的概率是.
故选:.
画树状图得出所有等可能的结果数以及三位同学抽到的课本都是自己课本的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
3.【答案】
【解析】【分析】
本题考查了概率的意义:一般地,在大量重复实验中,如果事件发生的频率会稳定在某个常数附近,那么这个常数就叫做事件的概率,记为;概率是频率多个的波动稳定值,是对事件发生可能性大小的量的表现.必然发生的事件的概率;不可能发生事件的概率.
根据概率的意义和必然发生的事件的概率、不可能发生事件的概率对、、进行判定;根据频率与概率的区别对进行判定.
【解答】
解:不可能事件发生的概率为,所以选项正确
B.随机事件发生的概率在与之间,所以选项错误
C.概率很小的事件不是不可能发生,而是发生的可能性较小,所以选项错误
D.投掷一枚质地均匀的硬币次,正面朝上的次数可能为次,所以选项错误.
故选A.
4.【答案】
【解析】【分析】
根据有理数的定义可找出在,,,,这个数中只有、和为有理数,再根据概率公式即可求出抽到有理数的概率.
本题考查了概率公式以及有理数,根据有理数的定义找出个数中的有理数的个数是解题的关键,还考查了概率计算公式,即概率所求情况数与总情况数之比.
【解答】
解:在,,,,这个数中只有,和为有理数,
从,,,,这个数中随机抽取一个数,抽到有理数的概率是.
故选:.
5.【答案】
【解析】解:画树状图如图:
共有种等可能的结果数,其中两人恰好选择同一场所的结果数为,
明明和亮亮两人恰好选择同一场馆的概率,
故选:.
画出树状图展示所有种等可能的结果数,找出两人恰好选择同一场所的结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
6.【答案】
【解析】【分析】
本题考查几何概率.
求出黑色区域的面积与整个地板面积的比值即可解决问题.
【解答】
解:由图可知,黑色区域的地板面积合起来等于两块正方形的面积,而地板总共有块正方形,
黑色区域面积在整个地板面积中所占的比值,
米粒停在黑色区域的概率是.
7.【答案】
【解析】【分析】
本题考查概率的求法与运用,一般方法为:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种结果,那么事件的概率.
根据随机事件概率大小的求法,找准两点:
符合条件的情况数目;
全部情况的总数.
二者的比值就是其发生的概率的大小.
【解答】
解:共个项目,“实验”项目有太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验共个,
随机选取一个项目写观后感,则恰好选到“实验”项目的概率是,
故选:.
8.【答案】
【解析】【分析】
此题主要考查了利用频率估计概率,根据大量反复试验下频率稳定值即概率是解题关键.
由摸到白球的频率稳定在附近得出口袋中得到白球的概率,进而求出黑球个数即可.
【解答】
解:设黑球个数为个,
摸到白球的频率稳定在附近,
口袋中得到红色球的概率为,
,
解得:,
经检验:是原方程的根,
故黑球的个数为个.
9.【答案】
【解析】解:,
,
,
,
,
可估计某品种小麦发芽情况的概率为,
则.
故选:.
根据次测试从粒增加到粒时,测试某品种小麦发芽情况的频率趋近于,从而求得答案.
本题考查了利用频率估计概率的知识,解题的关键是了解:大量反复试验下频率稳定值即概率.用到的知识点为:频率所求情况数与总情况数之比.
10.【答案】
【解析】解:画树状图如图所示.
因为可以组成的数有,,,,,,,,,,,,且是等可能性的,其中是“数”的有,,,,,,共六个,所以从,,,中任选两数,能与组成“数”的概率是.
11.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,其中摸出的两球的数字之和是的结果有种,
摸出的两球的数字之和是的概率是,
故答案为:.
画树状图,共有种等可能的结果,其中摸出的两球的数字之和是的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步或两步以上完成的事件;用到的知识点为:概率所求情况数与总情况数之比.
12.【答案】
【解析】略
13.【答案】
【解析】解:画树状图如图:
共有个等可能的结果,恰好摸出颗红球颗白球的结果有个,
恰好摸出颗红球颗白球的概率为,
故答案为:.
画树状图,共有个等可能的结果,恰好摸出颗红球颗白球的结果有个,再由概率公式求解即可.
此题考查的是用列表法或树状图法求概率.用到的知识点为:概率所求情况数与总情况数之比.
14.【答案】
【解析】解:从这批足球中,任意抽取一只足球是优等品的概率的估计值是.
故答案为:.
由表中数据可判断频率在左右摆动,于是利于频率估计概率可判断任意抽取一只足球是优等品的概率为.
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
15.【答案】;
,;
“等级”男女,从中选取人,所有可能出现的结果如下:
共有种可能出现的结果,其中女生被选中的有种,
女生被选中.
【解析】【分析】
本题考查条形统计图、扇形统计图的意义和制作方法,列表法求随机事件发生的概率,列举出所有可能出现的结果是求概率的前提.
等的有人,占调查人数的,可求出调查人数,进而求出等的人数;
等级占调查人数的,因此相应的圆心角为的即可,计算等级所占的百分比,即可求出的值;
用列表法表示所有可能出现的结果,进而求出相应的概率.
【解答】
解:名,名,
故答案为:;
,,即,
故答案为:,;
见答案.
16.【答案】解:;
组的人数为:名,
补全条形统计图如下:
;
名,
答:估计该校参加组阅读的学生人数为名;
画树状图如下:
共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,
恰好抽中甲、乙两人的概率为.
【解析】解:此次调查一共随机抽取的学生人数为:名,
故答案为:;
组的人数为:名,
补全条形统计图如下:
扇形统计图中圆心角,
故答案为:;
名,
答:估计该校参加组阅读的学生人数为名;
画树状图如下:
共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,
恰好抽中甲、乙两人的概率为.
由组的人数除以所占百分比即可;
求出组的人数,补全条形统计图即可;
由乘以组所占的比例即可;
由该校共有学生人数乘以参加组阅读的学生人数所占的比例即可;
画树状图,共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率以及条形统计图和扇形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
17.【答案】
【解析】解:被调查的总人数为人,
“部”对应的人数为人,
人数最多的数部,即众数为部,
处于中间位置的两个数据都是“部”,中位数为“部”
扇形统计图中“部”所在扇形的圆心角为,
故答案为:,,;
条形统计图如图所示,
地球脉动、蓝色星球、冰冻星球、地球的力量分别用字母、、、表示,
树状图如图所示:
一共有种等可能性,其中他们恰好选中同一部纪录片的可能性有种,
故他们恰好选中同一部纪录片的概率是,
即他们恰好选中同一部纪录片的概率是;
先求出被调查的总人数,继而求出“部”对应的人数,根据众数的定义可得答案,用乘以“部”人数所占比例即可;
根据以上所求结果即可补全图形即可;
列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
本题主要考查了扇形统计图以及条形统计图的运用,读懂统计图,从统计图中得到必要的信息是解题的关键;用到的知识点为:概率所求情况数与总情况数之比.
18.【答案】
【解析】解:杨老师从四个灯笼中任取一个,取到写有“一”的灯笼的概率是,
故答案为:;
画树状图如图:
共有个等可能的结果,杨老师恰好取到写有“军”“民”的两个灯笼的结果有个,
杨老师恰好取到写有“军”“民”的两个灯笼的概率为.
直接由概率公式求解即可;
画树状图,共有个等可能的结果,杨老师恰好取到写有“军”“民”的两个灯笼的结果有个,再由概率公式求解即可.
本题考查了列表法与树状图法,用到的知识点为:概率所求情况数与总情况数之比.
19.【答案】解:小明被分配到国家冬季两项中心场馆做志愿者的概率是;
画树状图如下:
共有种等可能的结果,其中小明和小颖被分配到同一场馆做志愿者的结果有种,
小明和小颖被分配到同一场馆做志愿者的概率为.
【解析】直接由概率公式求解即可;
画树状图,共有种等可能的结果,其中小明和小颖被分配到同一场馆做志愿者的结果有种,再由概率公式求解即可.
此题考查了用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
20.【答案】解:此次抽样调查的人数为:人;
接种类疫苗的人数的百分比为:,
接种类疫苗的人数为:人;
人,
即估计该小区所居住的名居民中有人进行了新冠疫苗接种.
画树状图如图:
共有种等可能的结果,恰好抽到一男和一女的结果有种,
恰好抽到一男和一女的概率为.
【解析】由类的人数除以所占百分比即可求解;
由接种类疫苗的人数除以此次抽样调查的人数得出此次抽样调查的人数所占的百分比,再由此次抽样调查的人数乘接种类疫苗的人数所占的百分比即可;
由该小区所居住的总人数乘、、三类所占的百分比之和即可;
画树状图,共有种等可能的结果,恰好抽到一男和一女的结果有种,再由概率公式求解即可.
此题考查的是用列表法或树状图法求概率以及条形统计图和扇形统计图.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
