19.2.2 一次函数的图象与性质课件
文档属性
| 名称 | 19.2.2 一次函数的图象与性质课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 954.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-10 00:00:00 | ||
图片预览

文档简介
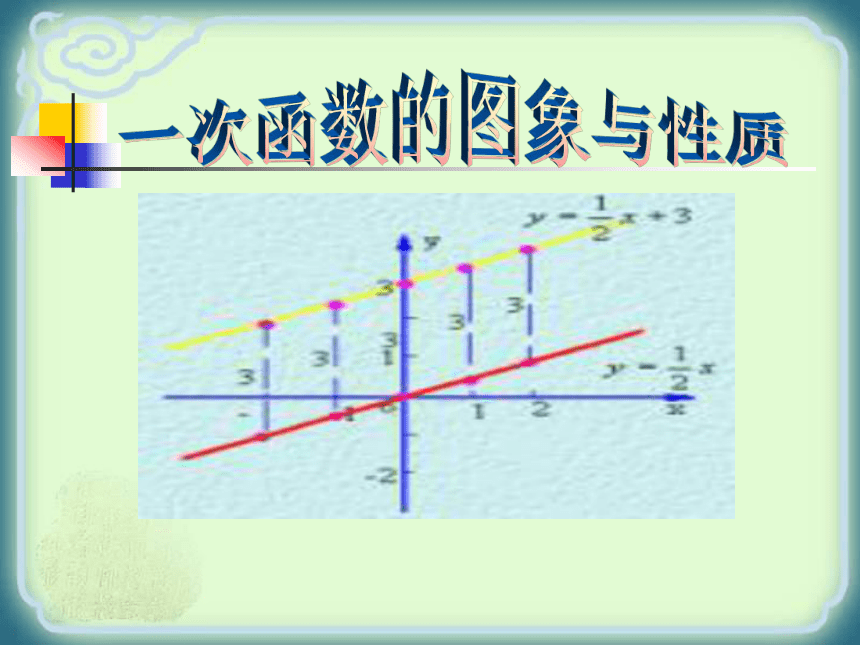
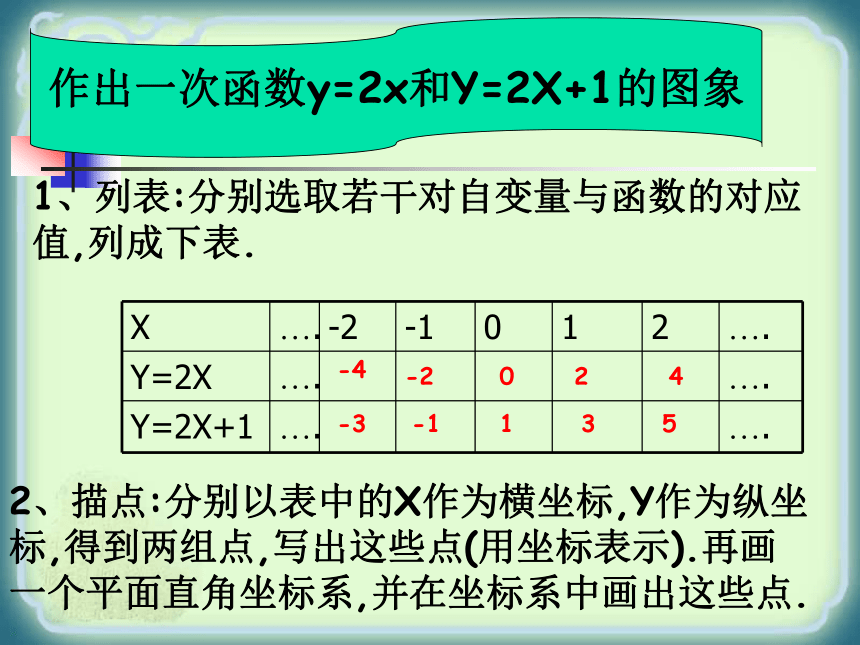
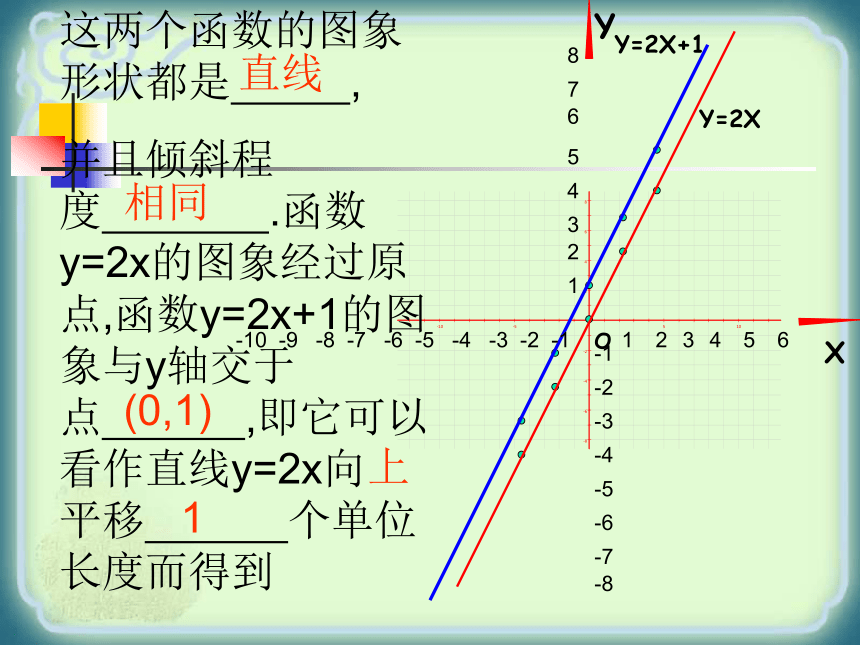
课件29张PPT。一次函数的图象与性质作出一次函数y=2x和Y=2X+1的图象1、列表:分别选取若干对自变量与函数的对应值,列成下表.2、描点:分别以表中的X作为横坐标,Y作为纵坐标,得到两组点,写出这些点(用坐标表示).再画一个平面直角坐标系,并在坐标系中画出这些点.-4-3-2-1012345YXOY=2XY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8这两个函数的图象形状都是 ,
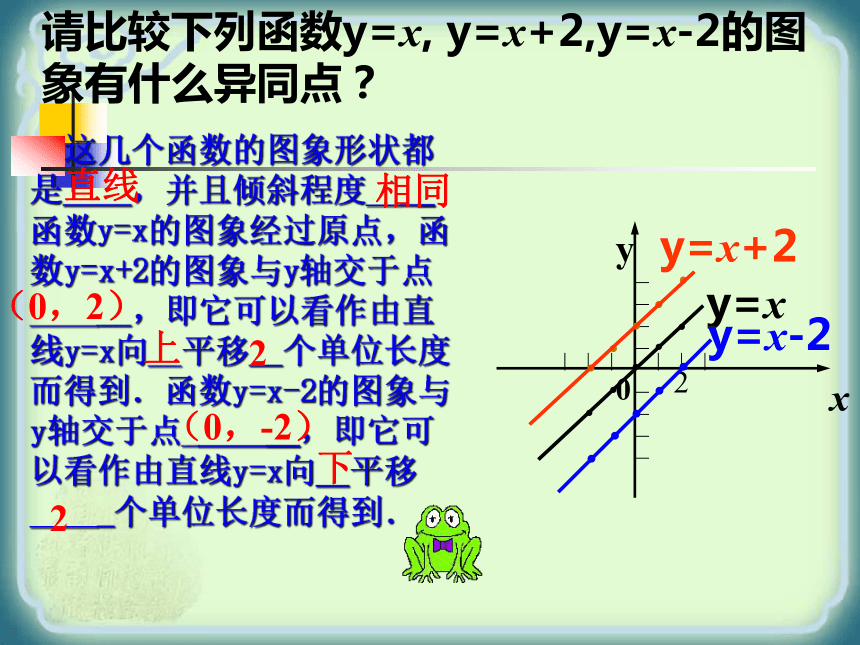
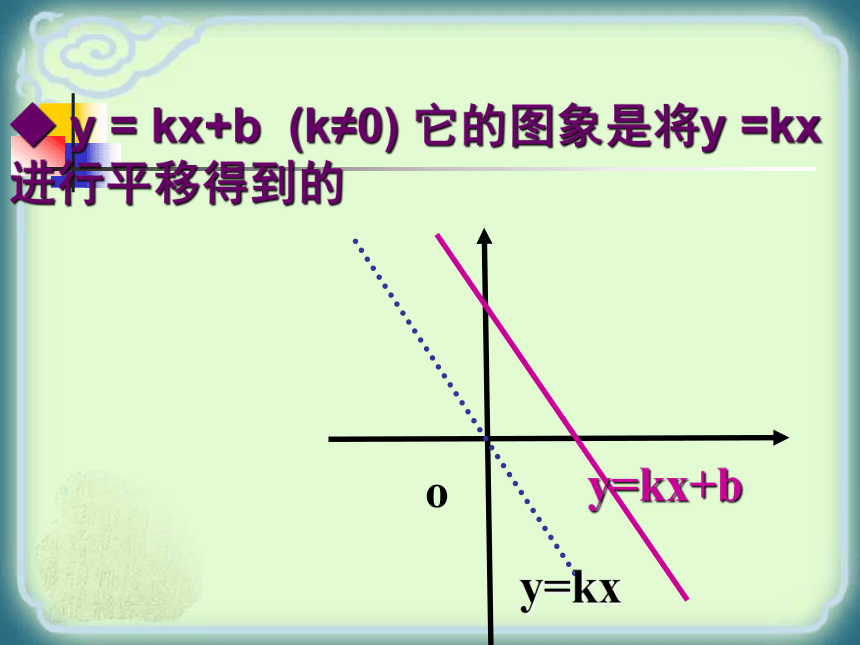
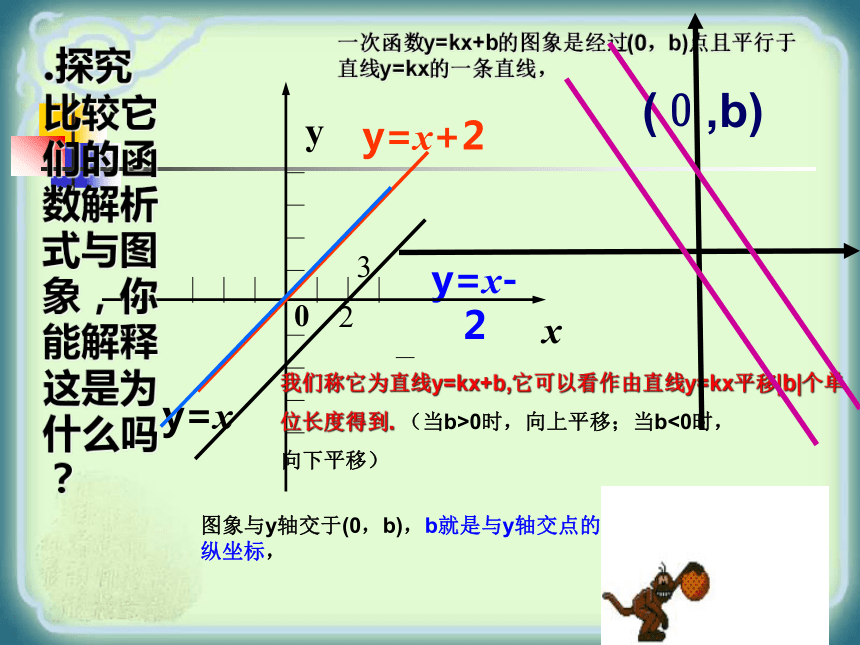
并且倾斜程度 .函数y=2x的图象经过原点,函数y=2x+1的图象与y轴交于点 ,即它可以看作直线y=2x向 平移 个单位长度而得到直线相同(0,1)上1.......请比较下列函数y=x, y=x+2,y=x-2的图象有什么异同点?....y=x....y=x+2y=x-2 这几个函数的图象形状都是 ,并且倾斜程度__ _函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.直线相同(0,2)上2(0,-2)下2◆ y = kx+b (k≠0) 它的图象是将y =kx 进行平移得到的
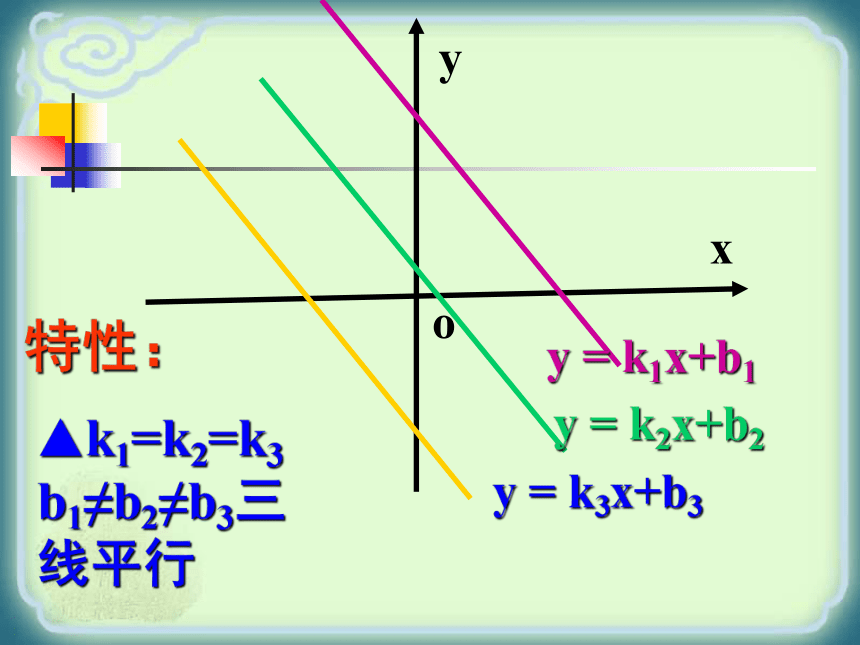
oy=kxy=kx+b特性:xyoy = k1x+b1▲k1=k2=k3 b1≠b2≠b3三线平行y = k2x+b2y = k3x+b3y=xy=x+2y=x-2y30.探究
比较它们的函数解析式与图象,你能解释这是为什么吗? 一次函数y=kx+b的图象是经过(0,b)点且平行于
直线y=kx的一条直线,
我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单
位长度得到. (当b>0时,向上平移;当b<0时,
向下平移)
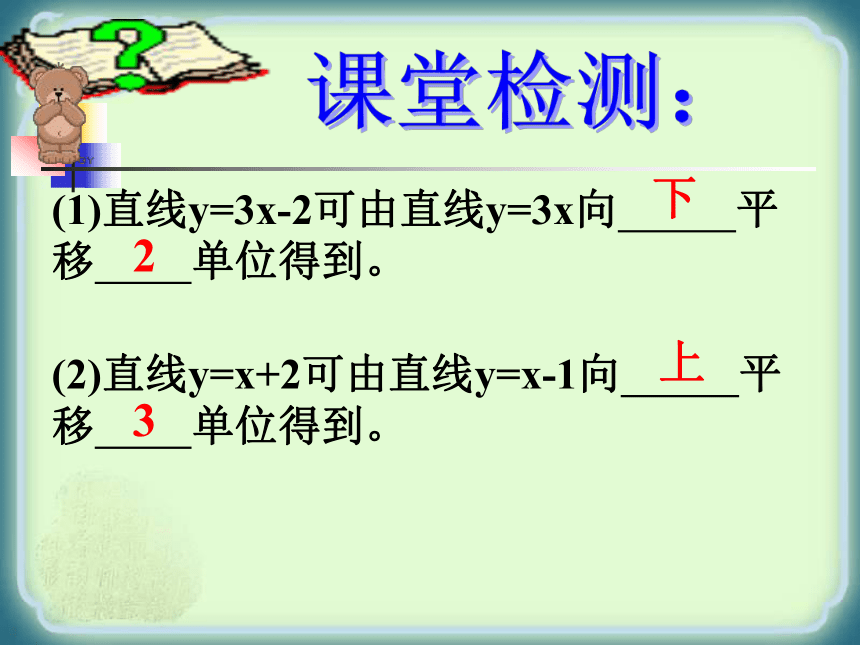
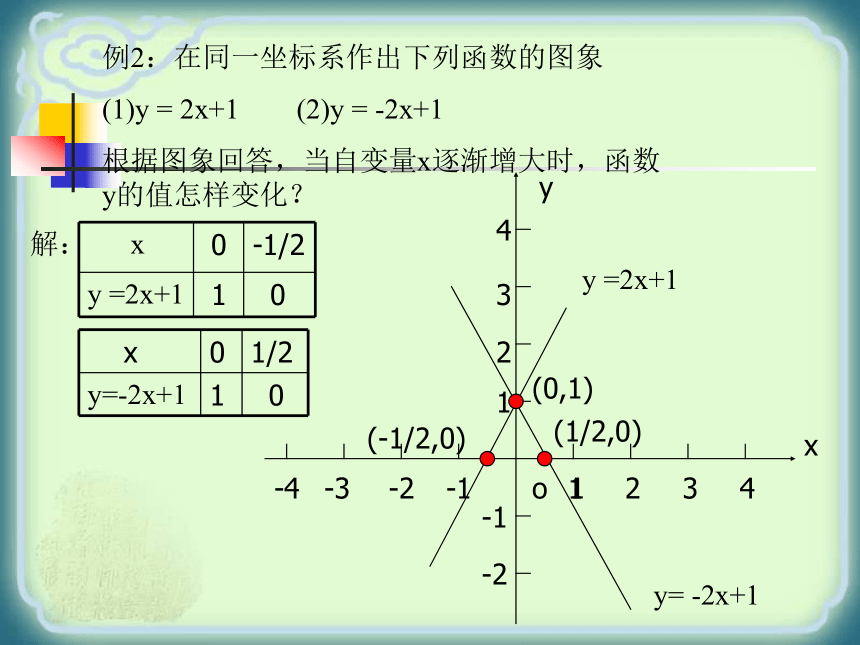
图象与y轴交于(0,b),b就是与y轴交点的纵坐标,(0,b)课堂检测:(1)直线y=3x-2可由直线y=3x向 平移 单位得到。(2)直线y=x+2可由直线y=x-1向 平移 单位得到。下2上3例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数y的值怎样变化?
解:y= -2x+1y =2x+1(0,1)(-1/2,0)(1/2,0)一次函数通常选取(0,b), (-b/k,0)两点连线 一次函数 y = kx + b ( k ≠ 0 ) 有以下性质:
(1)当 k > 0 时,y 随 x 的增大而 。
(2)当 k < 0 时,y 随 x 的增大而 。
增大减小一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大;
yx一次函数y=kx+b (k?0)的性质:当k<0时,y随x的增大而减小.yx一次函数图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0xx -5 -4 -3 -2 -154321-1 0-2-3-4-5 1 2 3 4 5xy1、有下列函数:①y=2x+1, ②y=-3x+4,
③ y=0.5x, ④y=x-6;①3 ④②③①函数y随x的增大而增大的是__________;其中过原点的直线是________;函数y随x的增大而减小的是___________;图象在第一、二、三象限的是________ 。练
一
练yxyx0
逆向思维
2、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B3、已知一次函数y = mx-(m-2),
若它的图象经过原点,则 m= ;
若点(0 ,3) 在它的图象上,则m = ;若它的图象经过一、二、四象限,则m .2-1<04.对于一次函数y = mx-(m-2),若y 随x 的增大而增小,则其图象不
过 象限。
5.若直线 y = kx -3 过(2, 5),
则k = ;
若此直线平行于直线y = - 3x - 5,
则k= .
三4-3
6、有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。②①、②、③③④7、函数y=(m – 1)x+1是一次函数,且y随自变量x增大而减小,那么m的取值为__________ m<18、已知一次函数y=2x+4的图象上有两点A(3,a),B(4,b),则a与b的大小关系为_________a (1) k为何值时,它的图象经过点(0, – 2);
(2)k为何值时,它的图象经过原点;
(3) k为何值时,它的图象与y轴的交点在x轴上方.
想一想 议一议 老师给出一个函数,甲、乙、丙、丁四位同学各指出这个函数的一个性质。甲:函数图象不经过第三象限;乙:函数图象经过第一象限;丙:当x<2时,y随x的增大而减小;丁:当x<2时,y>0. 已知这四位同学的叙述都正确,请构造出满足上述所有性质的一个函数。1、 如图,正方形ABCD的边长是4,将此正方形置于
平面直角坐标系中,使AB在x轴的正半轴上,点A的坐
标为(1,0)。
(1)过点C的直线 与x轴交于点E,
求四边形AECD的面积;
(2)若直线l过点E,且将ABCD分成面积相等的两部分,
求直线l的关系式。
AEBCD1Oxy2、 y= x–8343l 3、 画一画
在同一坐标系中,画出下列四个一次函数的 图 象:
(1)y=2x,
(2) y=2x+3 ,
(3) y=一2x,
(4) y=一2x+3 。
抢答题1在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限2已知一次函数y=x-2的大致图像为 ( )A B C D
已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。大显身手小结与回顾: 1、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
2、 一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线
2)当 k<0 时 y 随着x的增大而______ 。
两点法画一次函数图象:一次函数的性质:1)当 k>0 时 y 随着x的增大而______ 。增大减小一次函数y=kx+b(k ≠ 0)的图象特点:
⑴当k>0时,图象过______象限;
⑵当k<0时,图象过______象限。一、三二、四
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>K:决定直线倾斜的方向
b: 决定直线与y轴相交的交点的位置。
相交平行重合再见
并且倾斜程度 .函数y=2x的图象经过原点,函数y=2x+1的图象与y轴交于点 ,即它可以看作直线y=2x向 平移 个单位长度而得到直线相同(0,1)上1.......请比较下列函数y=x, y=x+2,y=x-2的图象有什么异同点?....y=x....y=x+2y=x-2 这几个函数的图象形状都是 ,并且倾斜程度__ _函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.直线相同(0,2)上2(0,-2)下2◆ y = kx+b (k≠0) 它的图象是将y =kx 进行平移得到的
oy=kxy=kx+b特性:xyoy = k1x+b1▲k1=k2=k3 b1≠b2≠b3三线平行y = k2x+b2y = k3x+b3y=xy=x+2y=x-2y30.探究
比较它们的函数解析式与图象,你能解释这是为什么吗? 一次函数y=kx+b的图象是经过(0,b)点且平行于
直线y=kx的一条直线,
我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单
位长度得到. (当b>0时,向上平移;当b<0时,
向下平移)
图象与y轴交于(0,b),b就是与y轴交点的纵坐标,(0,b)课堂检测:(1)直线y=3x-2可由直线y=3x向 平移 单位得到。(2)直线y=x+2可由直线y=x-1向 平移 单位得到。下2上3例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数y的值怎样变化?
解:y= -2x+1y =2x+1(0,1)(-1/2,0)(1/2,0)一次函数通常选取(0,b), (-b/k,0)两点连线 一次函数 y = kx + b ( k ≠ 0 ) 有以下性质:
(1)当 k > 0 时,y 随 x 的增大而 。
(2)当 k < 0 时,y 随 x 的增大而 。
增大减小一次函数y=kx+b (k?0)的性质:
当k>0时,y随x的增大而增大;
yx一次函数y=kx+b (k?0)的性质:当k<0时,y随x的增大而减小.yx一次函数图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0xx -5 -4 -3 -2 -154321-1 0-2-3-4-5 1 2 3 4 5xy1、有下列函数:①y=2x+1, ②y=-3x+4,
③ y=0.5x, ④y=x-6;①3 ④②③①函数y随x的增大而增大的是__________;其中过原点的直线是________;函数y随x的增大而减小的是___________;图象在第一、二、三象限的是________ 。练
一
练yxyx0
逆向思维
2、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B3、已知一次函数y = mx-(m-2),
若它的图象经过原点,则 m= ;
若点(0 ,3) 在它的图象上,则m = ;若它的图象经过一、二、四象限,则m .2-1<04.对于一次函数y = mx-(m-2),若y 随x 的增大而增小,则其图象不
过 象限。
5.若直线 y = kx -3 过(2, 5),
则k = ;
若此直线平行于直线y = - 3x - 5,
则k= .
三4-3
6、有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。②①、②、③③④7、函数y=(m – 1)x+1是一次函数,且y随自变量x增大而减小,那么m的取值为__________ m<18、已知一次函数y=2x+4的图象上有两点A(3,a),B(4,b),则a与b的大小关系为_________a
(2)k为何值时,它的图象经过原点;
(3) k为何值时,它的图象与y轴的交点在x轴上方.
想一想 议一议 老师给出一个函数,甲、乙、丙、丁四位同学各指出这个函数的一个性质。甲:函数图象不经过第三象限;乙:函数图象经过第一象限;丙:当x<2时,y随x的增大而减小;丁:当x<2时,y>0. 已知这四位同学的叙述都正确,请构造出满足上述所有性质的一个函数。1、 如图,正方形ABCD的边长是4,将此正方形置于
平面直角坐标系中,使AB在x轴的正半轴上,点A的坐
标为(1,0)。
(1)过点C的直线 与x轴交于点E,
求四边形AECD的面积;
(2)若直线l过点E,且将ABCD分成面积相等的两部分,
求直线l的关系式。
AEBCD1Oxy2、 y= x–8343l 3、 画一画
在同一坐标系中,画出下列四个一次函数的 图 象:
(1)y=2x,
(2) y=2x+3 ,
(3) y=一2x,
(4) y=一2x+3 。
抢答题1在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限2已知一次函数y=x-2的大致图像为 ( )A B C D
已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。大显身手小结与回顾: 1、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
2、 一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线
2)当 k<0 时 y 随着x的增大而______ 。
两点法画一次函数图象:一次函数的性质:1)当 k>0 时 y 随着x的增大而______ 。增大减小一次函数y=kx+b(k ≠ 0)的图象特点:
⑴当k>0时,图象过______象限;
⑵当k<0时,图象过______象限。一、三二、四
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>K:决定直线倾斜的方向
b: 决定直线与y轴相交的交点的位置。
相交平行重合再见
