24.1.1圆课件
图片预览










文档简介
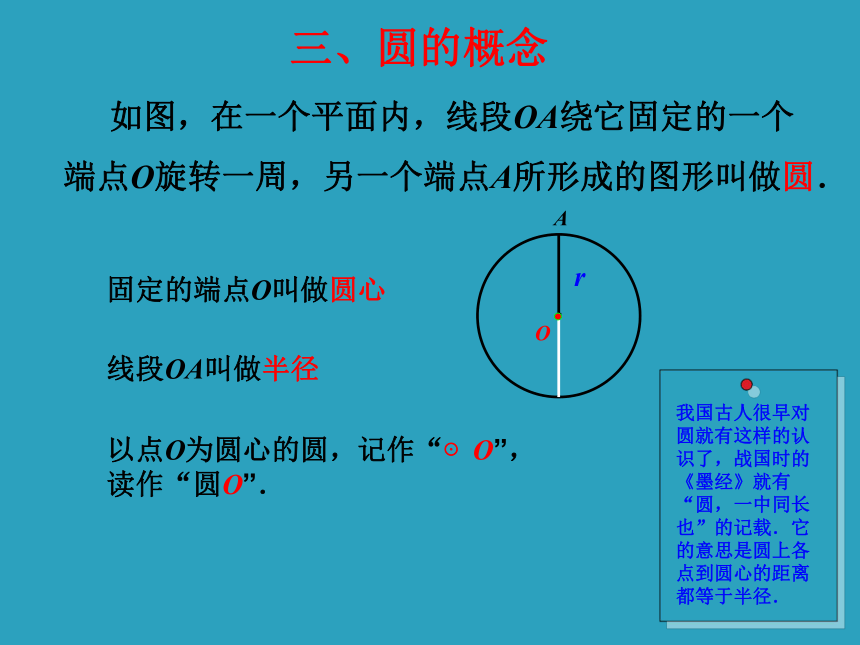
课件30张PPT。24.1.1 圆圆是生活中常见的图形,许多物体都给我们以圆的形象.一 感知圆的世界想一想,动手画圆!如果没有圆规,你还会画吗?超级链接: 画 圆.swf 如图,在一个平面内,线段OA绕它固定的一个
端点O旋转一周,另一个端点A所形成的图形叫做圆.固定的端点O叫做圆心线段OA叫做半径以点O为圆心的圆,记作“⊙O”,读作“圆O”.三、圆的概念(1)圆上各点到定点(圆心O)的距离都等于定长(半径r); 归纳:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点的集合.从画圆的过程可以看出:(2)到定点的距离等于定长的点都在同一个圆上.圆的两种定义动态:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形.确定一个圆的要素:圆心确定其位置,一是圆心,二是半径,半径确定其大小.
同步练习1、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周位置大小1.如何在操场上画一个半径是5m的圆?说出你的理由首先确定圆心, 然后用5米长的绳子一端固定为圆心端,另一端系在一端尖木棒,木棒以5米长尖端划动一周,所形成的图形就是所画的圆.根据圆的形成定义为什么车轮是圆的?议一议、说一说2、如果车轮做成三角形或正方形的,坐车的人会是什么感觉?超级链接: 车轮是圆的.swf 把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道理。圆上的点到圆心的距离是一个定值车轮为什么做成圆形的?归纳总结 经过圆心的弦(如图中的AB)叫做直径.·COAB连接圆上任意两点的线段(如图AC)叫做弦,与圆有关的概念弦议一议小明和小强为了探究 O中有没有最长的弦,
经过了大量的测量,最后得出一致结论,直径
是圆中最长的弦,你认为他们的结论对吗?
试说说你的理由.⊙弧圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 ,读作“圆弧AB”
AB”或“弧AB”.⌒AB圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.·ABCO·COAB劣弧与优弧小于半圆的弧(如图中的 )叫做劣弧;⌒AC大于半圆的弧(用三个字母表示,
如图中的 )叫做优弧.ABC⌒等圆与等弧能够重合的两个圆是等圆。容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等。在同圆或等圆中,能够互相重合的弧叫做等弧。同心圆:圆心相同而半径不等的两个圆或多个圆。同心圆超级链接:一石激起千层浪.swf想一想判断下列说法的正误:(1)弦是直径;(2)半圆是弧;(3)过圆心的线段是直径;(7)圆心相同,半径相等的两个圆是同心圆;(8)半径相等的两个圆是等圆.(4)过圆心的直线是直径;(5)半圆是最长的弧;(6)直径是最长的弦;( )( )( )( )( )( )( )( )9、圆中最长的弦长为12cm,则该圆的半径为 。 10、下列说法错误的有( )个
①经过P点的圆有无数个。
②以P为圆心的圆有无数个。
③半径为3cm且经过P点的圆有无数个。
④以P为圆心,以3cm为半径的圆有无数个。
A、1 B、2 C、3 D、4A6cm如图,请正确的方式表示出以点A为端点的优弧及劣弧. ⌒ACD⌒⌒⌒ACFADEADCACAEAFAD⌒⌒⌒⌒2 你见过树木的年轮吗?从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径每年增加多少?.解:
23÷2÷20=0.575cm 答: 这棵红衫树的半径每年增加0.575cm (三)应用迁移 巩固提高
类型之一 圆的有关概念
1/如图所示,点A、O、D以及点B、O、C分别在一条直线上,则圆中弦的条数为 ______。
2/下列说法中:
⑴①直径相等的两个圆是等圆;
②长度相等的两条弧是等弧;
③圆中最长的弦是通过圆心的弦;
④一条弦把圆分成两条弧,这两条弧不可能是等弧;
其中正确的是 ___________ 。⑵下列命题:
?矩形的四个顶点在同一个圆上,
?菱形四条边的中点在同一个圆上,
?等腰梯形的四个顶点在同一个圆上,
④直角三角形的三个顶点在以斜边为中点为圆心的同一个圆上。
其中正确的有———————— 3、如图,在⊙O中AB、CD为直径,请判断AD、BC的位置关系。
类型之二 圆在实际生活中的运用
4、导火索长18㎝,爆破时导火索燃烧的速度是每秒0.9㎝,点燃导火索的人需要跑到离爆破点120m以外的安全区域,这个点燃导火索的人每秒跑6.5m是否安全?类型之三 圆中的有关计算
5、一个点到圆的最小距离是4cm,最大距离是9cm,则该圆的直径是( )
A.2.5cm或.5cm B.2.5cm
C.6.5cm D.5cm或13cm
6、如图、已知CD是⊙O的直径,∠EOD=78°,AE交⊙O于点B,且AB=OC,求∠A的度数。 7、如图,AB、CD是⊙O的两条互相垂直的直径。
⑴ 试判断四边形ABCD是什么特殊的四边形?为什么?
⑵ 若⊙O的半径r=2㎝,求四边形ABCD的面积。【总结】
本节学习的数学知识是圆的定义和圆的有关概念。
本节学习的数学思想方法是转化思想。
【拓展】
1.如图,已知AB是的直径,CD是的弦,AB,CD的延长线相交于点E.
已知AB = 2DE,∠E = 18°,求∠AOC的度数.2.如图,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO都是矩形,
设BC = a,EF = b,NH = c,则下列各式正解的是( )
A.a>b>c B.a=b=c
C.c >a>b D. b>c> a 3、如图、在直角△ABC中,∠ACB=900,
AC=2,BC=4,以C为圆心,CA为半径的圆交斜边
于D,求:⑴AD的长,
⑵ △ BCD的面积。
端点O旋转一周,另一个端点A所形成的图形叫做圆.固定的端点O叫做圆心线段OA叫做半径以点O为圆心的圆,记作“⊙O”,读作“圆O”.三、圆的概念(1)圆上各点到定点(圆心O)的距离都等于定长(半径r); 归纳:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点的集合.从画圆的过程可以看出:(2)到定点的距离等于定长的点都在同一个圆上.圆的两种定义动态:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形.确定一个圆的要素:圆心确定其位置,一是圆心,二是半径,半径确定其大小.
同步练习1、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周位置大小1.如何在操场上画一个半径是5m的圆?说出你的理由首先确定圆心, 然后用5米长的绳子一端固定为圆心端,另一端系在一端尖木棒,木棒以5米长尖端划动一周,所形成的图形就是所画的圆.根据圆的形成定义为什么车轮是圆的?议一议、说一说2、如果车轮做成三角形或正方形的,坐车的人会是什么感觉?超级链接: 车轮是圆的.swf 把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道理。圆上的点到圆心的距离是一个定值车轮为什么做成圆形的?归纳总结 经过圆心的弦(如图中的AB)叫做直径.·COAB连接圆上任意两点的线段(如图AC)叫做弦,与圆有关的概念弦议一议小明和小强为了探究 O中有没有最长的弦,
经过了大量的测量,最后得出一致结论,直径
是圆中最长的弦,你认为他们的结论对吗?
试说说你的理由.⊙弧圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 ,读作“圆弧AB”
AB”或“弧AB”.⌒AB圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.·ABCO·COAB劣弧与优弧小于半圆的弧(如图中的 )叫做劣弧;⌒AC大于半圆的弧(用三个字母表示,
如图中的 )叫做优弧.ABC⌒等圆与等弧能够重合的两个圆是等圆。容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等。在同圆或等圆中,能够互相重合的弧叫做等弧。同心圆:圆心相同而半径不等的两个圆或多个圆。同心圆超级链接:一石激起千层浪.swf想一想判断下列说法的正误:(1)弦是直径;(2)半圆是弧;(3)过圆心的线段是直径;(7)圆心相同,半径相等的两个圆是同心圆;(8)半径相等的两个圆是等圆.(4)过圆心的直线是直径;(5)半圆是最长的弧;(6)直径是最长的弦;( )( )( )( )( )( )( )( )9、圆中最长的弦长为12cm,则该圆的半径为 。 10、下列说法错误的有( )个
①经过P点的圆有无数个。
②以P为圆心的圆有无数个。
③半径为3cm且经过P点的圆有无数个。
④以P为圆心,以3cm为半径的圆有无数个。
A、1 B、2 C、3 D、4A6cm如图,请正确的方式表示出以点A为端点的优弧及劣弧. ⌒ACD⌒⌒⌒ACFADEADCACAEAFAD⌒⌒⌒⌒2 你见过树木的年轮吗?从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径每年增加多少?.解:
23÷2÷20=0.575cm 答: 这棵红衫树的半径每年增加0.575cm (三)应用迁移 巩固提高
类型之一 圆的有关概念
1/如图所示,点A、O、D以及点B、O、C分别在一条直线上,则圆中弦的条数为 ______。
2/下列说法中:
⑴①直径相等的两个圆是等圆;
②长度相等的两条弧是等弧;
③圆中最长的弦是通过圆心的弦;
④一条弦把圆分成两条弧,这两条弧不可能是等弧;
其中正确的是 ___________ 。⑵下列命题:
?矩形的四个顶点在同一个圆上,
?菱形四条边的中点在同一个圆上,
?等腰梯形的四个顶点在同一个圆上,
④直角三角形的三个顶点在以斜边为中点为圆心的同一个圆上。
其中正确的有———————— 3、如图,在⊙O中AB、CD为直径,请判断AD、BC的位置关系。
类型之二 圆在实际生活中的运用
4、导火索长18㎝,爆破时导火索燃烧的速度是每秒0.9㎝,点燃导火索的人需要跑到离爆破点120m以外的安全区域,这个点燃导火索的人每秒跑6.5m是否安全?类型之三 圆中的有关计算
5、一个点到圆的最小距离是4cm,最大距离是9cm,则该圆的直径是( )
A.2.5cm或.5cm B.2.5cm
C.6.5cm D.5cm或13cm
6、如图、已知CD是⊙O的直径,∠EOD=78°,AE交⊙O于点B,且AB=OC,求∠A的度数。 7、如图,AB、CD是⊙O的两条互相垂直的直径。
⑴ 试判断四边形ABCD是什么特殊的四边形?为什么?
⑵ 若⊙O的半径r=2㎝,求四边形ABCD的面积。【总结】
本节学习的数学知识是圆的定义和圆的有关概念。
本节学习的数学思想方法是转化思想。
【拓展】
1.如图,已知AB是的直径,CD是的弦,AB,CD的延长线相交于点E.
已知AB = 2DE,∠E = 18°,求∠AOC的度数.2.如图,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO都是矩形,
设BC = a,EF = b,NH = c,则下列各式正解的是( )
A.a>b>c B.a=b=c
C.c >a>b D. b>c> a 3、如图、在直角△ABC中,∠ACB=900,
AC=2,BC=4,以C为圆心,CA为半径的圆交斜边
于D,求:⑴AD的长,
⑵ △ BCD的面积。
同课章节目录
