高中数学人教A版(2019)选修1 1.4 空间向量应用(二面角) 选择题专项章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)选修1 1.4 空间向量应用(二面角) 选择题专项章节综合练习题(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 867.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 17:41:43 | ||
图片预览



文档简介
登录二一教育在线组卷平台 助您教考全无忧
1.4 空间向量应用(二面角) 选择题专项
一、选择题
1.(2023·海盐开学考)在四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是矩形,且AB=3,AD=4,PA=,则锐二面角的大小为( )
A.30° B.45° C.60° D.75°
2.(2023·上虞模拟)如图,为直角梯形,.连,将沿翻折成三棱锥,当三棱锥外接球表面积的最小值时,二面角的余弦值为( )
A. B.0 C. D.
3.(2023·遂宁模拟)如图,正方体的棱长为2,线段上有两个动点(在的左边),且.下列说法不正确的是( )
A.当运动时,二面角的最小值为
B.当运动时,三棱锥体积不变
C.当运动时,存在点使得
D.当运动时,二面角为定值
4.(2023高二上·钦州期末)已知向量,分别为平面和平面的法向量,则平面与平面的夹角为( )
A. B. C. D.
5.(2022高二上·武汉期中)在正四面体中,点E在棱AB上,满足,点F为线段AC上的动点,则( )
A.存在某个位置,使得
B.存在某个位置,使得
C.存在某个位置,使得直线DE与平面DBF所成角的正弦值为
D.存在某个位置,使得平面DEF与平面DAC夹角的余弦值为
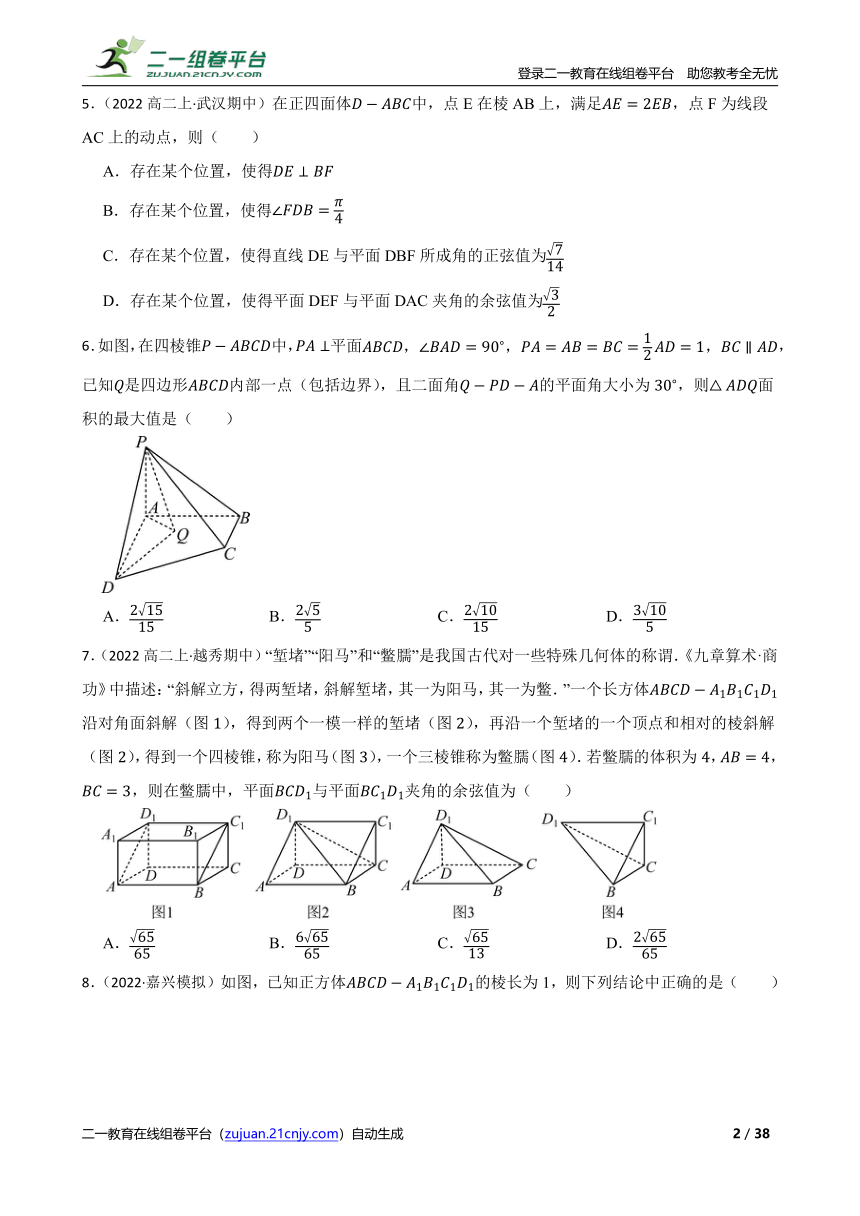
6.如图,在四棱锥中,平面,已知是四边形内部一点(包括边界),且二面角的平面角大小为,则面积的最大值是( )
A. B. C. D.
7.(2022高二上·越秀期中)“堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》中描述:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖.”一个长方体沿对角面斜解(图),得到两个一模一样的堑堵(图),再沿一个堑堵的一个顶点和相对的棱斜解(图),得到一个四棱锥,称为阳马(图),一个三棱锥称为鳖臑(图).若鳖臑的体积为,,,则在鳖臑中,平面与平面夹角的余弦值为( )
A. B. C. D.
8.(2022·嘉兴模拟)如图,已知正方体的棱长为1,则下列结论中正确的是( )
①若是直线上的动点,则平面②若是直线上的动点,则三棱锥的体积为定值③平面与平面所成的锐二面角的大小为④若是直线上的动点,则
A.①②③ B.②③④ C.①②④ D.①③④
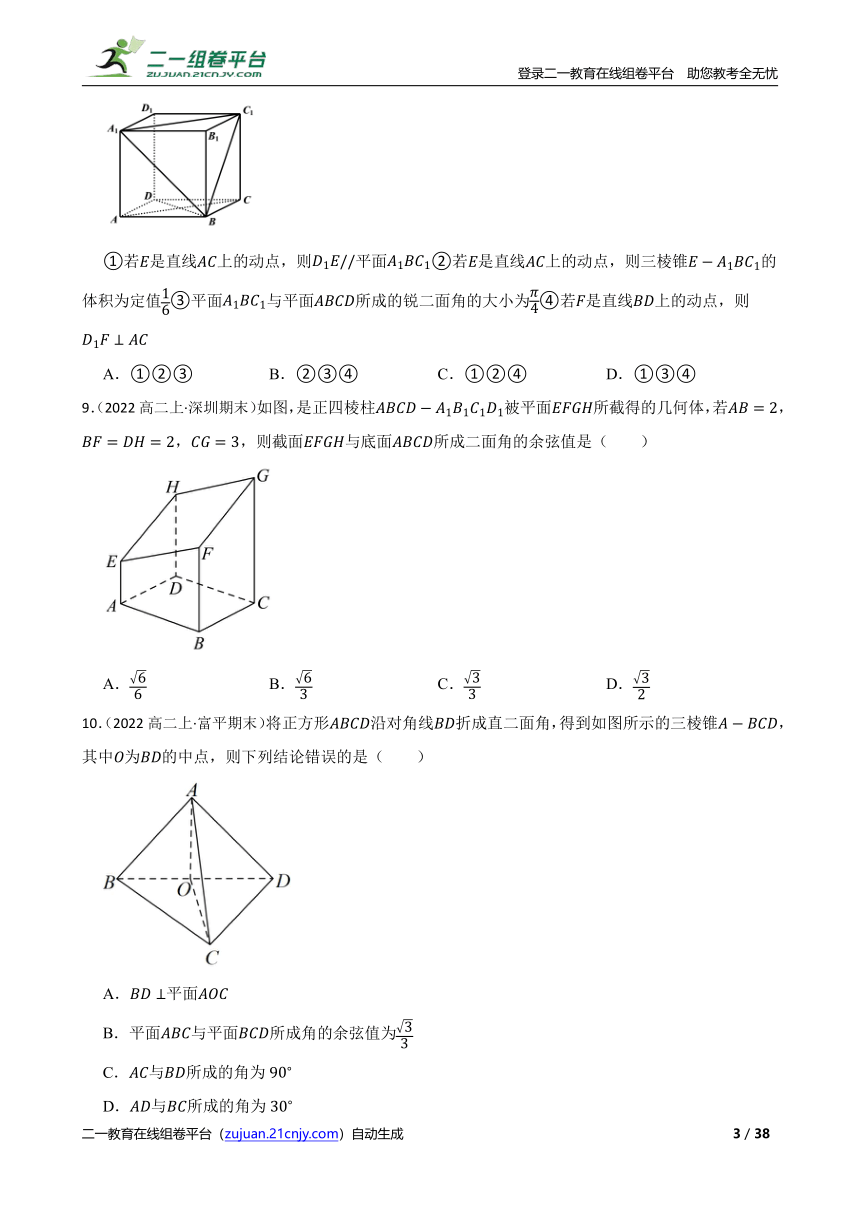
9.(2022高二上·深圳期末)如图,是正四棱柱被平面所截得的几何体,若,,,则截面与底面所成二面角的余弦值是( )
A. B. C. D.
10.(2022高二上·富平期末)将正方形沿对角线折成直二面角,得到如图所示的三棱锥,其中为的中点,则下列结论错误的是( )
A.平面
B.平面与平面所成角的余弦值为
C.与所成的角为
D.与所成的角为
11.(2021高二上·重庆市月考)在空间直角坐标系中,,,平面的一个法向量为,则平面与平面夹角的正弦值为( )
A. B. C. D.
12.(2021高二上·洮南月考)如图,在空间直角坐标系 中,四棱柱 为长方体, ,点 , 分别为 , 的中点,则二面角 的余弦值为( )
A. B. C. D.
13.(2021高二下·杭州期中)在棱长为2的正方体中,点在棱上,,点是棱的中点,点满足,当平面与平面所成(锐)二面角的余弦值为时,经过三点的截面的面积为( )
A. B. C. D.
14.(2020高二上·丽水期末)如图,正三角形 与正三角形 所在平面互相垂直,则二面角 的余弦值是( )
A. B. C. D.
15.(2020高二上·金华期末)如图,在正方形中,点 分别是线段 上的动点,且 与 交于G, 在 与 之间滑动,但与 和 均不重合.在 任一确定位置,将四边形 沿直线 折起,使平面 平面 ,则下列选项中错误的是( )
A. 的角度不会发生变化
B. 与 所成的角先变小后变大
C. 与平面 所成的角变小
D.二面角 先变大后变小
16.如图,在直三棱柱 中, , ,点 分别是线段 的中点, ,分别记二面角 , , 的平面角为 ,则下列结论正确的是( )
A. B. C. D.
17.(2020高二上·浙江月考)直三棱柱 中,若 , , 是 中点,过 作这个三棱柱的截面,当截面与平面 所成的锐二面角最小时,这个截面的面积为( )
A.2 B. C. D.
18.(2020高三上·温州月考)如图,在正四面体 中, ,记平面 与平面 平面 平面 ,所成的锐二面角分别为 ,则( )
A. B. C. D.
19.(2020高三上·宁波期中)如图,已知点 、 、G、 分别是正方体 中棱 、 、 、 的中点,记二面角 的平面角为 ,直线 与平面 所成角为 ,直线 与直线 所成角为 ,则( )
A. B. C. D.
20.在正方体 中,平面 与 所成二面角的余弦值为( )
A. B. C. D.
21.(2020高二下·杭州期末)如图,直三棱柱 的底面是边长为6的等边三角形,侧棱长为2,E是棱BC上的动点,F是棱 上靠近 点的三分点,M是棱 上的动点,则二面角 的正切值不可能是( )
A. B. C. D.
22.(2020高三上·浙江开学考)如图所示,在正三棱台 中, ,记侧面 与底面 ,侧面 与侧面 ,以及侧面 与截面 所成的锐二面角的平面角分别为 , , ,则( )
A. B. C. D.
23.(2020高二下·东海期中)《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑 中, 平面 , ,且 ,则二面角 的大小是( )
A.30° B.45° C.60° D.90°
24.(2020高二上·温州期末)正方形 沿对角线 折成直二面角,下列结论:① 与 所成的角为 :② 与 所成的角为 :③ 与面 所成角的正弦值为 :④二面角 的平面角正切值是 :其中正确结论的个数为( )
A.4 B.3 C.2 D.1
25.已知两平面的法向量分别为 , ,则两平面所成的二面角为( )
A. B.
C. 或 D.
26.如图,三棱柱 满足棱长都相等且 平面 ,D是棱 的中点,E是棱 上的动点.设 ,随着x增大,平面BDE与底面ABC所成锐二面角的平面角是( )
A.先增大再减小 B.减小
C.增大 D.先减小再增大
27.(2019·温州模拟)在四面体ABCD中, 为等边三角形, ,二面角 的大小为 ,则 的取值范围是( )
A. B. C. D.
28.(2019高三上·浙江月考)在正方体 中, 是底面 的中心, 是棱 上的点,且 ,记直线 与直线 所成角为 ,直线 与平面 所成角为 ,二面角 的平面角为 ,则( )
A. B. C. D.
29.(2019高三上·武汉月考)已知平面向量 , ,则 、 的夹角 ( )
A.150° B.120° C.60° D.30°
30.若平面 的一个法向量为 ,平面 的一个法向量是 ,则平面 与 所成的角等于( )
A.30° B.45° C.60° D.90°
答案解析部分
1.【答案】A
【解析】【解答】解:由题意知,,两两垂直,
以为坐标原点,,,所在直线为,,轴建立空间直角坐标系,
则 ,,,
易知平面的一个法向量为,设平面的一个法向量为
则,令,则,,锐二面角的大小为30°.
故答案为:A.
【分析】以为坐标原点,,,所在直线为,,轴建立空间直角坐标系,利用空间向量求锐二面角.
2.【答案】B
【解析】【解答】因为ABCD为直角梯形,AB//CD,AD⊥DC,AD=3,CD=,AB=,
所以AC= ,∠DAC=30°
∠BAC=60°,△ABC为等边三角形,△ACD为直角三角形,
设△ABC的中心为O1,AC的中点为E ,三棱锥 外接球的球心为O,
则OO1⊥平面ABC,OE⊥平面DAC,因为OA≥O1,所以三棱锥外接球表面积的最小,
即外接球的半径最小时, OA=O1A即O与O1重合,此时OE⊥平面DAC ,
即O1E⊥平面DAC,O1E 在平面ABC内,
故平面ABC⊥平面DAC,即二面角 为,余弦值为0.
故选:B.
【分析】 由题可得△ABC为等边三角形,设△ABC的中心为O1 ,AC的中点为E ,三棱锥 外接球的球心为O,根据球的性质可得O与O1重合时符合题意,即可求得二面角的余弦值.
3.【答案】C
【解析】【解答】对A:建立如图所示的空间直角坐标系,
则.
因为在上,且,,
可设,则,
则,
设平面的法向量为,
又,所以,即,
取,则,
平面的法向量为,所以.
设二面角的平面角为,则为锐角,故,
因为,在上单调递减,
所以,故,
当且仅当时,取得最大值,即取最小值,A说法正确.
对B:因为,点A到平面的距离为,
所以体积为,即体积为定值,B说法正确.
对C:若,则四点共面,与和是异面直线矛盾,C说法错误.
对D:连接,平面即为平面,而平面即为平面,故当运动时,二面角的大小保持不变,D说法正确.
故答案为:C
【分析】建立空间直角坐标系,利用向量法求解二面角夹角的余弦值,根据其范围,即可判断A;利用棱锥体积公式,即可求得三棱锥的体积,即可判断B;由反证法判断C;平面即为平面,而平面即为平面,从而得出二面角为定值,可判断D.
4.【答案】C
【解析】【解答】解:由已知可得,,,
所以.
设为平面与平面的夹角,则,
又,
所以.
故答案为:C.
【分析】根据坐标可求出,根据夹角的范围以及平面的夹角与平面法向量之间的关系即可求出答案.
5.【答案】C
【解析】【解答】如下图所示,设正四面体的底面中心为点,连接,则平面,
以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,
设正四面体的棱长为2,
则,,,,,
设,其中,
对于A,若存在某个位置使得,,,
所以,解得,不满足题意,A不符合题意;
对于B,若存在某个位置使得,,,
则,该方程无解,B不符合题意;
对于C,设平面的一个法向量为,
,,
由,令,则,
若存在某个位置,使得直线DE与平面DBF所成角的正弦值为,又,
则,
整理得,解得或(舍去),
所以存在,即为的中点,满足题意,C符合题意;
对于D,设平面的一个法向量为,
又,,
由,取,得,
设平面的一个法向量为,
,,
由,取,则,
若存在某个位置,使得平面DEF与平面DAC夹角的余弦值为,
则,
整理得,易得,所以该方程无解,D不符合题意.
故答案为:C.
【分析】以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法逐项进行判断,可得答案.
6.【答案】A
【解析】【解答】如图以A为坐标原点建立空间直角坐标系,
由二面角的平面角大小为30°,可知Q的轨迹是过点D的一条直线,
又Q是四边形ABCD内部一点(包括边界),
则Q的轨迹是过点D的一条线段,
设Q的轨迹与y轴的交点坐标为,
由题意可知,,,
所以,,,
易知平面APD的一个法向量为,
设平面PDG的法向量为,
则,即,
令,得,,
所以是平面PDG的一个法向量,
则二面角的平面角的余弦值为
,
解得或(舍去),
所以Q在DG上运动,
故面积的最大值是.
故答案为:A.
【分析】以A为坐标原点建立空间直角坐标系,根据题意得到点Q的轨迹是过点D的一条线段,设Q的轨迹与y轴的交点坐标为,分别求得平面和平面的法向量,结合向量的夹角公式列出方程,求得的值,进而求得面积的最大值.
7.【答案】B
【解析】【解答】由切割过程可知: 平面 ,
, ;
在长方体 中,以 为坐标原点, 正方向为 轴可建立如图所示空间直角坐标系,
则 , , , ,
, , ,
设平面 的法向量 ,
则 ,令 ,解得: , , ;
设平面 的法向量 ,
则 ,令 ,解得: , , ;
,
即平面 和平面 夹角的余弦值为 .
故答案为:B.
【分析】由切割过程可知: 平面 ,以 为坐标原点, 正方向为 轴可建立空间直角坐标系,利用向量法可求出平面 和平面 夹角的余弦值.
8.【答案】C
【解析】【解答】对于①,连接,
,,四边形为平行四边形,,
又平面,平面,平面,
同理可得:平面,
,平面,平面平面,
若是直线上的动点,则平面,平面,①正确;
对于②,由①知,平面,
,②正确;
对于③,连接,交于点,连接,
平面平面A1B1C1D1,平面与平面所成的锐二面角即为平面与平面A1B1C1D1所成的锐二面角,
四边形为正方形,,为中点,
又,,
即为平面与平面A1B1C1D1所成的锐二面角的平面角,
,,
即平面与平面所成的锐二面角不为,③错误;
对于④,四边形为正方形,,
平面,平面,,
又,平面,平面;
若是直线上的动点,则平面,,④正确.
故答案为:C.
【分析】由正方体的几何性质结合中点的性质即可得出线线平行,再由线面平行的判定定理即可判断出 ① 正确;由线面平行的性质定理结合距离的定义即可得出距离的取值,再由三棱锥的体积公式结合题意即可判断出 ② 正确;由正方体的几何性质结合二面角平面角的定义,由三角形中的几何计算关系计算出结果,从而判断出 ③ 错误;由线面垂直以及面面垂直的性质定理即可判断出 ④ 正确,从而得出答案。
9.【答案】B
【解析】【解答】如图所示:以为轴建立空间直角坐标系,
则,,,设平面的法向量为,
则,取得到,
平面的一个法向量为,,
故截面与底面所成二面角的余弦值是,
故答案为:B
【分析】根据棱柱的结构特征,以为轴建立空间直角坐标系,求出平面的法向量和平面的一个法向量,利用向量法可求出截面与底面所成二面角的余弦值.
10.【答案】D
【解析】【解答】因为折叠前为正方形,由题意则折叠后有,,
又平面,平面,,所以平面,A符合题意;
又平面,所以,与所成的角为,C符合题意;
因为二面角为直二面角,而平面,
所以为二面角的平面角,即,
如图所示,以所在直线为轴建立空间直角坐标系,
设,则,
,,
设平面的法向量为,
则令,则可得,
取平面的法向量为,
平面与平面所成角的余弦值为,B符合题意;
设与所成的角为,则,
又因为,所以,D不符合题意.
故答案为:D.
【分析】根据题意,利用线面垂直的判定定理可证明A;由于平面,可判断C;以所在直线为轴建立空间直角坐标系,设出三棱锥的棱长,求出平面ABC与平面BCD的法向量,计算可判断B;求出AD与BC的方向向量,通过其方向向量计算出异面直线所成的角,可判断D.
11.【答案】A
【解析】【解答】设平面的法向量为,则,令,得,令平面与平面夹角为,则,,所以平面与平面夹角的正弦值为。
故答案为:A
【分析】利用已知条件结合空间向量数量积求夹角公式,从而求出平面与平面夹角的余弦值,再结合同角三角函数基本关系式,从而求出平面与平面夹角的正弦值,进而求出平面与平面夹角的正弦值。
12.【答案】C
【解析】【解答】解:设AD=1,则A1(1,0,2),B(1,2,0).
∵E为C1D1的中点,
∴E(0,1,2),
∴,
设是平面A1BE的法向量,
则∴
∴y=x ,y=z
取x=1,则y=z=1,
平面ABE的一个法向量为,
又DA⊥平面A1B1B,
是平面A1B1B的一个法向量,
∴
又二面角B1-A1B-E为锐二面角,
∴二面角B1-A1B-E的余弦值为
故答案为:C
【分析】利用向量法直接求解即可.
13.【答案】B
【解析】【解答】解:如图,以D为坐标原点,分别以 所在的直线为 轴,建立空间直角坐标系,
则 ,所以 ,
设平面 的一个法向量为 ,则
,取 ,则 ,
平面 的一个法向量为 ,
由题意得 ,解得 或 (舍去),
延长 ,设 ,连接 ,交 于 ,延长 ,交 的延长线于 ,连接 ,交 于 ,则五边形 为截面图形,
由题意求得 , , , , , ,截面五边形 如图所示,
则等腰三角形 底边 上的高为 ,等腰梯形 的高为 ,
则截面面积为
故答案为:B
【分析】以D为坐标原点,分别以 所在的直线为 轴,建立空间直角坐标系,由空间向量结合平面与平面所成(锐)二面角的余弦值为求得,画出截面图,求得截面五边形的边长,再由等腰三角形及等腰梯形的面积作和即可得解.
14.【答案】D
【解析】【解答】如图示,取AC中点E,连结BE、DE,在正三角形 与正三角形 中,
BE⊥AC,DE⊥AC,因为面 ⊥面 ,面 面 ,所以BE⊥面ADC,
以E为原点, 为x轴正方向, 为y轴正方向, 为z轴正方向,建立空间直角坐标系,设AC=2,则
,
平面ACD的一个法向量为
而 ,设 为面BCD的一个法向量,则:
即 ,不妨令x=1,则
设二面角 的平面角为θ,则θ为锐角,
所以 .
故答案为:D
【分析】首先由已知条件的面面垂直即可得出线面垂直,再由线面垂直的性质定理即可得出线线垂直由此建立空间直角坐标系求出各个点的坐标以及向量和平面ACD法向量的坐标,再由数量积的坐标公式即可求出平面BCD的法向量的坐标,结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到二面角的余弦值。
15.【答案】D
【解析】【解答】以 为原点, , , 所在的直线为 轴,
建立空间直角坐标系,
设正方形的边长为 , ,
, , , , ,
对于A, , ,
,
故 的角度不会发生变化,所以A符合题意;
对于B,设 与 所成的角为 ,
, ,
,
对称轴为 ,且 ,所以 先减小后增加,
所以 先增加再减小,即 与 所成的角先变小后变大,B符合题意;
对于C,平面 的一个法向量为 ,
设 与平面 所成的角为 ,
,
,则 单调递减, 单调递减,
所以 与平面 所成的角变小,C符合题意;
对于D,设平面 的法向量为 ,
则 ,即 ,
令 , , ,
不妨设 ,
设平面 的一个法向量为 ,
则 , ,
令 , ,即 ,
,
对称轴为 ,在 先减小后增大,
所以 在 先减小后增大,
二面角 为钝角,
先增大后减小,
故二面角 先减小后增大,D不符合题意.
故答案为:D
【分析】以 为原点, , , 所在的直线为 轴,建立空间直角坐标系,进而求出点的坐标,再利用折叠的方法结合数量积求向量夹角公式和二次函数的图象的单调性,进而找出错误的选项。
16.【答案】D
【解析】【解答】解:因为 , ,所以 ,即
过点 作 ,以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
则 ,0, , , , , ,0, , ,1, ,
, ,
, , ,
设平面 的法向量 ,
则 ,取 ,得 ,
同理可求平面 的法向量 ,
平面 的法向量 ,平面 的法向量 .
, , .
.
故答案为:D.
【分析】以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,利用向量法求解二面角的余弦值即可得到答案。
17.【答案】C
【解析】【解答】解:因为 , ,所以 ,即 .
所以根据题意,以 点为坐标原点, 分别为 轴建立空间直角坐标系,
则 , , , ,
易知平面 的法向量为 , 设截面的法向量为 ,
则 ,即 ,
设截面与平面 所成的锐二面角为 ,
则
所以当 时, 取最大值,锐二面角为 取最小,
不妨设 ,则 , ,即 ,
此时,过 截面与 平面内的直线 的交点为 ,
则 ,所以 ,即 ,解得 ,
过 截面与 平面内的直线 的交点为 ,
则 ,所以 ,即 ,解得 ,
所以 , ,
所以此时截面即为四边形 ,
其中 , , , ,
则在四边形 中, ,
所以 ,
所以四边形 的面积为
.
故答案为:C.
【分析】以 点为坐标原点, 分别为 轴建立空间直角坐标系,设截面的法向量为 ,设截面与平面 所成的锐二面角为 ,平面 的法向量为 ,则 ,即 ,则 ,故 取最大值,锐二面角为 取最小,即 ,过 截面与 平面内的直线 的交点为 ,由 ,即 ,即可求出答案。
18.【答案】A
【解析】【解答】解:(空间向量法)
因为 ,所以E F分别为 的中点,G为 上靠近A的三等分点,取 的中点M,连接 ,
过A作 平面 ,交 于点O,在平面 中过O作 ,交 于N,设正四面体 的棱长为2,则 , , ,
以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,
, , , , , , , , , , , ,
设平面 的一个法向量为 ,则 ,
即 ,不妨令 ,则 ,
同理可计算出平面 平面 平面 的一个法向量分别为 , , ,
则可得 , , ,
所以 ,
又 在 上递减,所以 ,
故答案为:A.
【分析】过A作 平面 ,取 的中点M,连接 ,交 于点O,以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,利用坐标向量法先求,再根据余弦函数单调性比较大小即可。
19.【答案】D
【解析】【解答】解:如图建立空间直角坐标系,令正方体的棱长为 ,
则 , , , , , , , ,
显然面 的法向量为 ,设面 的法向量为 ,则 ,即 ,令 则 、 ,所以
所以 , ,所以 ,
因为 ,即 ,所以
故答案为:D
【分析】建立空间直角坐标系,利用空间向量法求出线面角、二面角、异面直角所成角,即可比较;
20.【答案】C
【解析】【解答】以点 为原点, , , 所在直线分别为 轴、 轴、 轴建立空间直角坐标系,如图所示,
设正方体的棱长为1,则 , , , , ,
∴ , , , ,
∴ 和 分别是平面 和平面 的法向量,
又 ,结合图形可知平面 与平面 所成二面角的余弦值为 .
故答案为:C.
【分析】先建立空间直角坐标系,求出平面 与 的法向量,根据向量的夹角余弦公式即可求出.
21.【答案】B
【解析】【解答】取 的中点O,连接 ,根据等边三角形的性质可知 ,
根据直三棱柱的性质,以O为原点建立如图所示的空间直角坐标系.
则 ,设 .
则 .
设平面 的一个法向量为 ,
则 ,
令 ,得 .
平面 的一个法向量是 ,
所以 ,
所以 ,
所以二面角 的正切值为:
.
因为 ,所以 ,
结合二次函数的性质可知:
当 时, 有最小值为 ;
当 时, 有最大值为 ,
所以 ,
所以二面角 的正切值不可能是 .
故答案为:B
【分析】建立空间直角坐标系,求得二面角 的余弦值,进而求得二面角 的正切值,得到正切值的最小值,由此判断出正确选项.
22.【答案】B
【解析】【解答】解:如图,取 中点 , 中点 ,连接 , ,
设 的中心为 , 的中心为 ,
则根据正三角形的中心与重心重合得 分别为 的三等分点,且 , ,
由于在正三棱台 中, ,
所以 , ,
由正三棱台的性质得 平面 , 平面 ,
过 点作 于 ,
根据几何关系易知 , , , ,
故以 点为坐标原点,如图建立空间直角坐标系,
所以 , , ,
, , ,
易知 是平面 的法向量,
设平面 的法向量为 ,平面 的法向量为 ,平面 的法向量为 ,
由于 , ,
所以 ,即 ,故 ,
所以 ,
所以侧面 与底面 所成锐二面角余弦值为 ,即 ,
由于 , , ,
同理可得平面 的法向量为 ,平面 的法向量为 ,
所以 , ,
所以侧面 与侧面 所成锐二面角余弦值为 ,即 ,
侧面 与截面 所成锐二面角余弦值为 ,即 ,
由于 , , ,均为锐角, ,
所以 .
故答案为:B.
【分析】设 的中心为 , 的中心为 ,以 点为坐标原点,如图建立空间直角坐标系,分别求出所涉及四个平面的一个法向量,利用法向量求解所成锐二面角的余弦值,结合余弦函数的单调性得答案.
23.【答案】C
【解析】【解答】解:如图建立空间直角坐标系,
因为 ,所以 , , , , ,
显然面 的一个法向量可以为 ,
设面 的法向量为
则 ,即 ,令 则 , ,所以
设二面角 为 ,则
所以
故答案为:C
【分析】根据题意建立空间直角坐标系求出各个点的坐标以及向量和平面法向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到二面角 的大小即可。
24.【答案】A
【解析】【解答】解:取 中点O,连结 , ,
∵正方形 沿对角线 折成直二面角,
∴以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,
设 ,则 , , , ,
, ,
,
∴异面直线 与 所成的角为 ,故①正确:
, ,
∵ ,∴ ,故②正确:
设平面 的一个法向量为 ,
由 ,取 ,得 , ,
设 与面 所成角为 ,则 ,故③正确:
平面 的法向量 , , ,
设平面 的法向量 ,
则 ,取 ,得 ,
,
∴ .
∴二面角 的平面角正切值是: ,故④正确.
故答案为:A.
【分析】取 中点O,连结 , ,以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,利用向量法和空间中线线、线面、面面间的位置关系逐一判断四个命题得结论.
25.【答案】C
【解析】【解答】∵两平面的法向量分别为
则两平面所成的二面角与 相等或互补
故 .
故两平面所成的二面角为45°或135°
故答案为:C.
【分析】根据已知中两个平面法向量的夹角,代入向量夹角公式,可以求出两个向量的夹角,进而根据两平面所成的二面角与 相等或互补,得到答案.
26.【答案】D
【解析】【解答】以 中点 为坐标原点, 分别为 轴,并垂直向上作 轴建立空间直角坐标系.
设所有棱长均为2,则 , , ,设平面BDE法向量 则 ,令 有 ,
故 .又平面ABC的法向量 ,故平面BDE与底面ABC所成锐二面角的平面角 的余弦值
,又 ,故 在 上单增, 上单减,即随着x增大先变大后变小,所一以 随着x增大先变小后变大.
故答案为:D.
【分析】可直接建立空间直角坐标系求解平面BDE与底面ABC所成锐二面角的余弦值 关于 的函数,再分析函数的单调性即可.
27.【答案】C
【解析】【解答】以B为原点建立如图所示的空间直角坐标系:
因为 为等边三角形,不妨设 ,
由于 ,所以
因为当 时 四点共面,不能构成空间四边形,所以
则 , ,
由空间向量的坐标运算可得
设平面 的法向量为
则 代入可得
令 ,则 ,所以
设平面 的法向量为
则 ,代入可得
令 ,则 ,所以
二面角 的大小为
则由图可知,二面角 为锐二面角
所以
因为
所以
即
所以
故答案为:C
【分析】以B为原点建立空间直角坐标系,根据关系写出各个点的坐标,利用平面 和平面 的法向量,表示出二面角 的余弦值,即可求得 的取值范围.
28.【答案】C
【解析】【解答】解:以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
设正方体 中棱长为4,
则 ,
, ,
= = ,
平面 的法向量 ,
∴ = ,∴ = ,
, ,
设平面 的法向量 ,
则 ,取 ,得 ,
= ,
∵ ,∴ .
故答案为:C.
【分析】以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,推导出 ,由此得到 .
29.【答案】A
【解析】【解答】解: ,
因为 ,
所以 ,
故答案为:A.
【分析】利用向量的夹角公式直接求解即可.
30.【答案】D
【解析】【解答】依题意得, ,
则 ,
所以平面 平面 ,
即 与 所成的角是 ,
故答案为:D.
【分析】根据空间向量夹角的余弦公式可求出两平面法向量的余弦值为0,从而得到答案。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
1.4 空间向量应用(二面角) 选择题专项
一、选择题
1.(2023·海盐开学考)在四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是矩形,且AB=3,AD=4,PA=,则锐二面角的大小为( )
A.30° B.45° C.60° D.75°
2.(2023·上虞模拟)如图,为直角梯形,.连,将沿翻折成三棱锥,当三棱锥外接球表面积的最小值时,二面角的余弦值为( )
A. B.0 C. D.
3.(2023·遂宁模拟)如图,正方体的棱长为2,线段上有两个动点(在的左边),且.下列说法不正确的是( )
A.当运动时,二面角的最小值为
B.当运动时,三棱锥体积不变
C.当运动时,存在点使得
D.当运动时,二面角为定值
4.(2023高二上·钦州期末)已知向量,分别为平面和平面的法向量,则平面与平面的夹角为( )
A. B. C. D.
5.(2022高二上·武汉期中)在正四面体中,点E在棱AB上,满足,点F为线段AC上的动点,则( )
A.存在某个位置,使得
B.存在某个位置,使得
C.存在某个位置,使得直线DE与平面DBF所成角的正弦值为
D.存在某个位置,使得平面DEF与平面DAC夹角的余弦值为
6.如图,在四棱锥中,平面,已知是四边形内部一点(包括边界),且二面角的平面角大小为,则面积的最大值是( )
A. B. C. D.
7.(2022高二上·越秀期中)“堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》中描述:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖.”一个长方体沿对角面斜解(图),得到两个一模一样的堑堵(图),再沿一个堑堵的一个顶点和相对的棱斜解(图),得到一个四棱锥,称为阳马(图),一个三棱锥称为鳖臑(图).若鳖臑的体积为,,,则在鳖臑中,平面与平面夹角的余弦值为( )
A. B. C. D.
8.(2022·嘉兴模拟)如图,已知正方体的棱长为1,则下列结论中正确的是( )
①若是直线上的动点,则平面②若是直线上的动点,则三棱锥的体积为定值③平面与平面所成的锐二面角的大小为④若是直线上的动点,则
A.①②③ B.②③④ C.①②④ D.①③④
9.(2022高二上·深圳期末)如图,是正四棱柱被平面所截得的几何体,若,,,则截面与底面所成二面角的余弦值是( )
A. B. C. D.
10.(2022高二上·富平期末)将正方形沿对角线折成直二面角,得到如图所示的三棱锥,其中为的中点,则下列结论错误的是( )
A.平面
B.平面与平面所成角的余弦值为
C.与所成的角为
D.与所成的角为
11.(2021高二上·重庆市月考)在空间直角坐标系中,,,平面的一个法向量为,则平面与平面夹角的正弦值为( )
A. B. C. D.
12.(2021高二上·洮南月考)如图,在空间直角坐标系 中,四棱柱 为长方体, ,点 , 分别为 , 的中点,则二面角 的余弦值为( )
A. B. C. D.
13.(2021高二下·杭州期中)在棱长为2的正方体中,点在棱上,,点是棱的中点,点满足,当平面与平面所成(锐)二面角的余弦值为时,经过三点的截面的面积为( )
A. B. C. D.
14.(2020高二上·丽水期末)如图,正三角形 与正三角形 所在平面互相垂直,则二面角 的余弦值是( )
A. B. C. D.
15.(2020高二上·金华期末)如图,在正方形中,点 分别是线段 上的动点,且 与 交于G, 在 与 之间滑动,但与 和 均不重合.在 任一确定位置,将四边形 沿直线 折起,使平面 平面 ,则下列选项中错误的是( )
A. 的角度不会发生变化
B. 与 所成的角先变小后变大
C. 与平面 所成的角变小
D.二面角 先变大后变小
16.如图,在直三棱柱 中, , ,点 分别是线段 的中点, ,分别记二面角 , , 的平面角为 ,则下列结论正确的是( )
A. B. C. D.
17.(2020高二上·浙江月考)直三棱柱 中,若 , , 是 中点,过 作这个三棱柱的截面,当截面与平面 所成的锐二面角最小时,这个截面的面积为( )
A.2 B. C. D.
18.(2020高三上·温州月考)如图,在正四面体 中, ,记平面 与平面 平面 平面 ,所成的锐二面角分别为 ,则( )
A. B. C. D.
19.(2020高三上·宁波期中)如图,已知点 、 、G、 分别是正方体 中棱 、 、 、 的中点,记二面角 的平面角为 ,直线 与平面 所成角为 ,直线 与直线 所成角为 ,则( )
A. B. C. D.
20.在正方体 中,平面 与 所成二面角的余弦值为( )
A. B. C. D.
21.(2020高二下·杭州期末)如图,直三棱柱 的底面是边长为6的等边三角形,侧棱长为2,E是棱BC上的动点,F是棱 上靠近 点的三分点,M是棱 上的动点,则二面角 的正切值不可能是( )
A. B. C. D.
22.(2020高三上·浙江开学考)如图所示,在正三棱台 中, ,记侧面 与底面 ,侧面 与侧面 ,以及侧面 与截面 所成的锐二面角的平面角分别为 , , ,则( )
A. B. C. D.
23.(2020高二下·东海期中)《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑 中, 平面 , ,且 ,则二面角 的大小是( )
A.30° B.45° C.60° D.90°
24.(2020高二上·温州期末)正方形 沿对角线 折成直二面角,下列结论:① 与 所成的角为 :② 与 所成的角为 :③ 与面 所成角的正弦值为 :④二面角 的平面角正切值是 :其中正确结论的个数为( )
A.4 B.3 C.2 D.1
25.已知两平面的法向量分别为 , ,则两平面所成的二面角为( )
A. B.
C. 或 D.
26.如图,三棱柱 满足棱长都相等且 平面 ,D是棱 的中点,E是棱 上的动点.设 ,随着x增大,平面BDE与底面ABC所成锐二面角的平面角是( )
A.先增大再减小 B.减小
C.增大 D.先减小再增大
27.(2019·温州模拟)在四面体ABCD中, 为等边三角形, ,二面角 的大小为 ,则 的取值范围是( )
A. B. C. D.
28.(2019高三上·浙江月考)在正方体 中, 是底面 的中心, 是棱 上的点,且 ,记直线 与直线 所成角为 ,直线 与平面 所成角为 ,二面角 的平面角为 ,则( )
A. B. C. D.
29.(2019高三上·武汉月考)已知平面向量 , ,则 、 的夹角 ( )
A.150° B.120° C.60° D.30°
30.若平面 的一个法向量为 ,平面 的一个法向量是 ,则平面 与 所成的角等于( )
A.30° B.45° C.60° D.90°
答案解析部分
1.【答案】A
【解析】【解答】解:由题意知,,两两垂直,
以为坐标原点,,,所在直线为,,轴建立空间直角坐标系,
则 ,,,
易知平面的一个法向量为,设平面的一个法向量为
则,令,则,,锐二面角的大小为30°.
故答案为:A.
【分析】以为坐标原点,,,所在直线为,,轴建立空间直角坐标系,利用空间向量求锐二面角.
2.【答案】B
【解析】【解答】因为ABCD为直角梯形,AB//CD,AD⊥DC,AD=3,CD=,AB=,
所以AC= ,∠DAC=30°
∠BAC=60°,△ABC为等边三角形,△ACD为直角三角形,
设△ABC的中心为O1,AC的中点为E ,三棱锥 外接球的球心为O,
则OO1⊥平面ABC,OE⊥平面DAC,因为OA≥O1,所以三棱锥外接球表面积的最小,
即外接球的半径最小时, OA=O1A即O与O1重合,此时OE⊥平面DAC ,
即O1E⊥平面DAC,O1E 在平面ABC内,
故平面ABC⊥平面DAC,即二面角 为,余弦值为0.
故选:B.
【分析】 由题可得△ABC为等边三角形,设△ABC的中心为O1 ,AC的中点为E ,三棱锥 外接球的球心为O,根据球的性质可得O与O1重合时符合题意,即可求得二面角的余弦值.
3.【答案】C
【解析】【解答】对A:建立如图所示的空间直角坐标系,
则.
因为在上,且,,
可设,则,
则,
设平面的法向量为,
又,所以,即,
取,则,
平面的法向量为,所以.
设二面角的平面角为,则为锐角,故,
因为,在上单调递减,
所以,故,
当且仅当时,取得最大值,即取最小值,A说法正确.
对B:因为,点A到平面的距离为,
所以体积为,即体积为定值,B说法正确.
对C:若,则四点共面,与和是异面直线矛盾,C说法错误.
对D:连接,平面即为平面,而平面即为平面,故当运动时,二面角的大小保持不变,D说法正确.
故答案为:C
【分析】建立空间直角坐标系,利用向量法求解二面角夹角的余弦值,根据其范围,即可判断A;利用棱锥体积公式,即可求得三棱锥的体积,即可判断B;由反证法判断C;平面即为平面,而平面即为平面,从而得出二面角为定值,可判断D.
4.【答案】C
【解析】【解答】解:由已知可得,,,
所以.
设为平面与平面的夹角,则,
又,
所以.
故答案为:C.
【分析】根据坐标可求出,根据夹角的范围以及平面的夹角与平面法向量之间的关系即可求出答案.
5.【答案】C
【解析】【解答】如下图所示,设正四面体的底面中心为点,连接,则平面,
以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,
设正四面体的棱长为2,
则,,,,,
设,其中,
对于A,若存在某个位置使得,,,
所以,解得,不满足题意,A不符合题意;
对于B,若存在某个位置使得,,,
则,该方程无解,B不符合题意;
对于C,设平面的一个法向量为,
,,
由,令,则,
若存在某个位置,使得直线DE与平面DBF所成角的正弦值为,又,
则,
整理得,解得或(舍去),
所以存在,即为的中点,满足题意,C符合题意;
对于D,设平面的一个法向量为,
又,,
由,取,得,
设平面的一个法向量为,
,,
由,取,则,
若存在某个位置,使得平面DEF与平面DAC夹角的余弦值为,
则,
整理得,易得,所以该方程无解,D不符合题意.
故答案为:C.
【分析】以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法逐项进行判断,可得答案.
6.【答案】A
【解析】【解答】如图以A为坐标原点建立空间直角坐标系,
由二面角的平面角大小为30°,可知Q的轨迹是过点D的一条直线,
又Q是四边形ABCD内部一点(包括边界),
则Q的轨迹是过点D的一条线段,
设Q的轨迹与y轴的交点坐标为,
由题意可知,,,
所以,,,
易知平面APD的一个法向量为,
设平面PDG的法向量为,
则,即,
令,得,,
所以是平面PDG的一个法向量,
则二面角的平面角的余弦值为
,
解得或(舍去),
所以Q在DG上运动,
故面积的最大值是.
故答案为:A.
【分析】以A为坐标原点建立空间直角坐标系,根据题意得到点Q的轨迹是过点D的一条线段,设Q的轨迹与y轴的交点坐标为,分别求得平面和平面的法向量,结合向量的夹角公式列出方程,求得的值,进而求得面积的最大值.
7.【答案】B
【解析】【解答】由切割过程可知: 平面 ,
, ;
在长方体 中,以 为坐标原点, 正方向为 轴可建立如图所示空间直角坐标系,
则 , , , ,
, , ,
设平面 的法向量 ,
则 ,令 ,解得: , , ;
设平面 的法向量 ,
则 ,令 ,解得: , , ;
,
即平面 和平面 夹角的余弦值为 .
故答案为:B.
【分析】由切割过程可知: 平面 ,以 为坐标原点, 正方向为 轴可建立空间直角坐标系,利用向量法可求出平面 和平面 夹角的余弦值.
8.【答案】C
【解析】【解答】对于①,连接,
,,四边形为平行四边形,,
又平面,平面,平面,
同理可得:平面,
,平面,平面平面,
若是直线上的动点,则平面,平面,①正确;
对于②,由①知,平面,
,②正确;
对于③,连接,交于点,连接,
平面平面A1B1C1D1,平面与平面所成的锐二面角即为平面与平面A1B1C1D1所成的锐二面角,
四边形为正方形,,为中点,
又,,
即为平面与平面A1B1C1D1所成的锐二面角的平面角,
,,
即平面与平面所成的锐二面角不为,③错误;
对于④,四边形为正方形,,
平面,平面,,
又,平面,平面;
若是直线上的动点,则平面,,④正确.
故答案为:C.
【分析】由正方体的几何性质结合中点的性质即可得出线线平行,再由线面平行的判定定理即可判断出 ① 正确;由线面平行的性质定理结合距离的定义即可得出距离的取值,再由三棱锥的体积公式结合题意即可判断出 ② 正确;由正方体的几何性质结合二面角平面角的定义,由三角形中的几何计算关系计算出结果,从而判断出 ③ 错误;由线面垂直以及面面垂直的性质定理即可判断出 ④ 正确,从而得出答案。
9.【答案】B
【解析】【解答】如图所示:以为轴建立空间直角坐标系,
则,,,设平面的法向量为,
则,取得到,
平面的一个法向量为,,
故截面与底面所成二面角的余弦值是,
故答案为:B
【分析】根据棱柱的结构特征,以为轴建立空间直角坐标系,求出平面的法向量和平面的一个法向量,利用向量法可求出截面与底面所成二面角的余弦值.
10.【答案】D
【解析】【解答】因为折叠前为正方形,由题意则折叠后有,,
又平面,平面,,所以平面,A符合题意;
又平面,所以,与所成的角为,C符合题意;
因为二面角为直二面角,而平面,
所以为二面角的平面角,即,
如图所示,以所在直线为轴建立空间直角坐标系,
设,则,
,,
设平面的法向量为,
则令,则可得,
取平面的法向量为,
平面与平面所成角的余弦值为,B符合题意;
设与所成的角为,则,
又因为,所以,D不符合题意.
故答案为:D.
【分析】根据题意,利用线面垂直的判定定理可证明A;由于平面,可判断C;以所在直线为轴建立空间直角坐标系,设出三棱锥的棱长,求出平面ABC与平面BCD的法向量,计算可判断B;求出AD与BC的方向向量,通过其方向向量计算出异面直线所成的角,可判断D.
11.【答案】A
【解析】【解答】设平面的法向量为,则,令,得,令平面与平面夹角为,则,,所以平面与平面夹角的正弦值为。
故答案为:A
【分析】利用已知条件结合空间向量数量积求夹角公式,从而求出平面与平面夹角的余弦值,再结合同角三角函数基本关系式,从而求出平面与平面夹角的正弦值,进而求出平面与平面夹角的正弦值。
12.【答案】C
【解析】【解答】解:设AD=1,则A1(1,0,2),B(1,2,0).
∵E为C1D1的中点,
∴E(0,1,2),
∴,
设是平面A1BE的法向量,
则∴
∴y=x ,y=z
取x=1,则y=z=1,
平面ABE的一个法向量为,
又DA⊥平面A1B1B,
是平面A1B1B的一个法向量,
∴
又二面角B1-A1B-E为锐二面角,
∴二面角B1-A1B-E的余弦值为
故答案为:C
【分析】利用向量法直接求解即可.
13.【答案】B
【解析】【解答】解:如图,以D为坐标原点,分别以 所在的直线为 轴,建立空间直角坐标系,
则 ,所以 ,
设平面 的一个法向量为 ,则
,取 ,则 ,
平面 的一个法向量为 ,
由题意得 ,解得 或 (舍去),
延长 ,设 ,连接 ,交 于 ,延长 ,交 的延长线于 ,连接 ,交 于 ,则五边形 为截面图形,
由题意求得 , , , , , ,截面五边形 如图所示,
则等腰三角形 底边 上的高为 ,等腰梯形 的高为 ,
则截面面积为
故答案为:B
【分析】以D为坐标原点,分别以 所在的直线为 轴,建立空间直角坐标系,由空间向量结合平面与平面所成(锐)二面角的余弦值为求得,画出截面图,求得截面五边形的边长,再由等腰三角形及等腰梯形的面积作和即可得解.
14.【答案】D
【解析】【解答】如图示,取AC中点E,连结BE、DE,在正三角形 与正三角形 中,
BE⊥AC,DE⊥AC,因为面 ⊥面 ,面 面 ,所以BE⊥面ADC,
以E为原点, 为x轴正方向, 为y轴正方向, 为z轴正方向,建立空间直角坐标系,设AC=2,则
,
平面ACD的一个法向量为
而 ,设 为面BCD的一个法向量,则:
即 ,不妨令x=1,则
设二面角 的平面角为θ,则θ为锐角,
所以 .
故答案为:D
【分析】首先由已知条件的面面垂直即可得出线面垂直,再由线面垂直的性质定理即可得出线线垂直由此建立空间直角坐标系求出各个点的坐标以及向量和平面ACD法向量的坐标,再由数量积的坐标公式即可求出平面BCD的法向量的坐标,结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到二面角的余弦值。
15.【答案】D
【解析】【解答】以 为原点, , , 所在的直线为 轴,
建立空间直角坐标系,
设正方形的边长为 , ,
, , , , ,
对于A, , ,
,
故 的角度不会发生变化,所以A符合题意;
对于B,设 与 所成的角为 ,
, ,
,
对称轴为 ,且 ,所以 先减小后增加,
所以 先增加再减小,即 与 所成的角先变小后变大,B符合题意;
对于C,平面 的一个法向量为 ,
设 与平面 所成的角为 ,
,
,则 单调递减, 单调递减,
所以 与平面 所成的角变小,C符合题意;
对于D,设平面 的法向量为 ,
则 ,即 ,
令 , , ,
不妨设 ,
设平面 的一个法向量为 ,
则 , ,
令 , ,即 ,
,
对称轴为 ,在 先减小后增大,
所以 在 先减小后增大,
二面角 为钝角,
先增大后减小,
故二面角 先减小后增大,D不符合题意.
故答案为:D
【分析】以 为原点, , , 所在的直线为 轴,建立空间直角坐标系,进而求出点的坐标,再利用折叠的方法结合数量积求向量夹角公式和二次函数的图象的单调性,进而找出错误的选项。
16.【答案】D
【解析】【解答】解:因为 , ,所以 ,即
过点 作 ,以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
则 ,0, , , , , ,0, , ,1, ,
, ,
, , ,
设平面 的法向量 ,
则 ,取 ,得 ,
同理可求平面 的法向量 ,
平面 的法向量 ,平面 的法向量 .
, , .
.
故答案为:D.
【分析】以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,利用向量法求解二面角的余弦值即可得到答案。
17.【答案】C
【解析】【解答】解:因为 , ,所以 ,即 .
所以根据题意,以 点为坐标原点, 分别为 轴建立空间直角坐标系,
则 , , , ,
易知平面 的法向量为 , 设截面的法向量为 ,
则 ,即 ,
设截面与平面 所成的锐二面角为 ,
则
所以当 时, 取最大值,锐二面角为 取最小,
不妨设 ,则 , ,即 ,
此时,过 截面与 平面内的直线 的交点为 ,
则 ,所以 ,即 ,解得 ,
过 截面与 平面内的直线 的交点为 ,
则 ,所以 ,即 ,解得 ,
所以 , ,
所以此时截面即为四边形 ,
其中 , , , ,
则在四边形 中, ,
所以 ,
所以四边形 的面积为
.
故答案为:C.
【分析】以 点为坐标原点, 分别为 轴建立空间直角坐标系,设截面的法向量为 ,设截面与平面 所成的锐二面角为 ,平面 的法向量为 ,则 ,即 ,则 ,故 取最大值,锐二面角为 取最小,即 ,过 截面与 平面内的直线 的交点为 ,由 ,即 ,即可求出答案。
18.【答案】A
【解析】【解答】解:(空间向量法)
因为 ,所以E F分别为 的中点,G为 上靠近A的三等分点,取 的中点M,连接 ,
过A作 平面 ,交 于点O,在平面 中过O作 ,交 于N,设正四面体 的棱长为2,则 , , ,
以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,
, , , , , , , , , , , ,
设平面 的一个法向量为 ,则 ,
即 ,不妨令 ,则 ,
同理可计算出平面 平面 平面 的一个法向量分别为 , , ,
则可得 , , ,
所以 ,
又 在 上递减,所以 ,
故答案为:A.
【分析】过A作 平面 ,取 的中点M,连接 ,交 于点O,以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,利用坐标向量法先求,再根据余弦函数单调性比较大小即可。
19.【答案】D
【解析】【解答】解:如图建立空间直角坐标系,令正方体的棱长为 ,
则 , , , , , , , ,
显然面 的法向量为 ,设面 的法向量为 ,则 ,即 ,令 则 、 ,所以
所以 , ,所以 ,
因为 ,即 ,所以
故答案为:D
【分析】建立空间直角坐标系,利用空间向量法求出线面角、二面角、异面直角所成角,即可比较;
20.【答案】C
【解析】【解答】以点 为原点, , , 所在直线分别为 轴、 轴、 轴建立空间直角坐标系,如图所示,
设正方体的棱长为1,则 , , , , ,
∴ , , , ,
∴ 和 分别是平面 和平面 的法向量,
又 ,结合图形可知平面 与平面 所成二面角的余弦值为 .
故答案为:C.
【分析】先建立空间直角坐标系,求出平面 与 的法向量,根据向量的夹角余弦公式即可求出.
21.【答案】B
【解析】【解答】取 的中点O,连接 ,根据等边三角形的性质可知 ,
根据直三棱柱的性质,以O为原点建立如图所示的空间直角坐标系.
则 ,设 .
则 .
设平面 的一个法向量为 ,
则 ,
令 ,得 .
平面 的一个法向量是 ,
所以 ,
所以 ,
所以二面角 的正切值为:
.
因为 ,所以 ,
结合二次函数的性质可知:
当 时, 有最小值为 ;
当 时, 有最大值为 ,
所以 ,
所以二面角 的正切值不可能是 .
故答案为:B
【分析】建立空间直角坐标系,求得二面角 的余弦值,进而求得二面角 的正切值,得到正切值的最小值,由此判断出正确选项.
22.【答案】B
【解析】【解答】解:如图,取 中点 , 中点 ,连接 , ,
设 的中心为 , 的中心为 ,
则根据正三角形的中心与重心重合得 分别为 的三等分点,且 , ,
由于在正三棱台 中, ,
所以 , ,
由正三棱台的性质得 平面 , 平面 ,
过 点作 于 ,
根据几何关系易知 , , , ,
故以 点为坐标原点,如图建立空间直角坐标系,
所以 , , ,
, , ,
易知 是平面 的法向量,
设平面 的法向量为 ,平面 的法向量为 ,平面 的法向量为 ,
由于 , ,
所以 ,即 ,故 ,
所以 ,
所以侧面 与底面 所成锐二面角余弦值为 ,即 ,
由于 , , ,
同理可得平面 的法向量为 ,平面 的法向量为 ,
所以 , ,
所以侧面 与侧面 所成锐二面角余弦值为 ,即 ,
侧面 与截面 所成锐二面角余弦值为 ,即 ,
由于 , , ,均为锐角, ,
所以 .
故答案为:B.
【分析】设 的中心为 , 的中心为 ,以 点为坐标原点,如图建立空间直角坐标系,分别求出所涉及四个平面的一个法向量,利用法向量求解所成锐二面角的余弦值,结合余弦函数的单调性得答案.
23.【答案】C
【解析】【解答】解:如图建立空间直角坐标系,
因为 ,所以 , , , , ,
显然面 的一个法向量可以为 ,
设面 的法向量为
则 ,即 ,令 则 , ,所以
设二面角 为 ,则
所以
故答案为:C
【分析】根据题意建立空间直角坐标系求出各个点的坐标以及向量和平面法向量的坐标,再由数量积的坐标公式即可求出平面的法向量的坐标结合空间数量积的运算公式代入数值即可求出夹角的余弦值,由此得到二面角 的大小即可。
24.【答案】A
【解析】【解答】解:取 中点O,连结 , ,
∵正方形 沿对角线 折成直二面角,
∴以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,
设 ,则 , , , ,
, ,
,
∴异面直线 与 所成的角为 ,故①正确:
, ,
∵ ,∴ ,故②正确:
设平面 的一个法向量为 ,
由 ,取 ,得 , ,
设 与面 所成角为 ,则 ,故③正确:
平面 的法向量 , , ,
设平面 的法向量 ,
则 ,取 ,得 ,
,
∴ .
∴二面角 的平面角正切值是: ,故④正确.
故答案为:A.
【分析】取 中点O,连结 , ,以O为原点, 为x轴, 为y轴, 为z轴,建立空间直角坐标系,利用向量法和空间中线线、线面、面面间的位置关系逐一判断四个命题得结论.
25.【答案】C
【解析】【解答】∵两平面的法向量分别为
则两平面所成的二面角与 相等或互补
故 .
故两平面所成的二面角为45°或135°
故答案为:C.
【分析】根据已知中两个平面法向量的夹角,代入向量夹角公式,可以求出两个向量的夹角,进而根据两平面所成的二面角与 相等或互补,得到答案.
26.【答案】D
【解析】【解答】以 中点 为坐标原点, 分别为 轴,并垂直向上作 轴建立空间直角坐标系.
设所有棱长均为2,则 , , ,设平面BDE法向量 则 ,令 有 ,
故 .又平面ABC的法向量 ,故平面BDE与底面ABC所成锐二面角的平面角 的余弦值
,又 ,故 在 上单增, 上单减,即随着x增大先变大后变小,所一以 随着x增大先变小后变大.
故答案为:D.
【分析】可直接建立空间直角坐标系求解平面BDE与底面ABC所成锐二面角的余弦值 关于 的函数,再分析函数的单调性即可.
27.【答案】C
【解析】【解答】以B为原点建立如图所示的空间直角坐标系:
因为 为等边三角形,不妨设 ,
由于 ,所以
因为当 时 四点共面,不能构成空间四边形,所以
则 , ,
由空间向量的坐标运算可得
设平面 的法向量为
则 代入可得
令 ,则 ,所以
设平面 的法向量为
则 ,代入可得
令 ,则 ,所以
二面角 的大小为
则由图可知,二面角 为锐二面角
所以
因为
所以
即
所以
故答案为:C
【分析】以B为原点建立空间直角坐标系,根据关系写出各个点的坐标,利用平面 和平面 的法向量,表示出二面角 的余弦值,即可求得 的取值范围.
28.【答案】C
【解析】【解答】解:以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
设正方体 中棱长为4,
则 ,
, ,
= = ,
平面 的法向量 ,
∴ = ,∴ = ,
, ,
设平面 的法向量 ,
则 ,取 ,得 ,
= ,
∵ ,∴ .
故答案为:C.
【分析】以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,推导出 ,由此得到 .
29.【答案】A
【解析】【解答】解: ,
因为 ,
所以 ,
故答案为:A.
【分析】利用向量的夹角公式直接求解即可.
30.【答案】D
【解析】【解答】依题意得, ,
则 ,
所以平面 平面 ,
即 与 所成的角是 ,
故答案为:D.
【分析】根据空间向量夹角的余弦公式可求出两平面法向量的余弦值为0,从而得到答案。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
