专题12 带电粒子在磁场中运动--2023高考物理分类解析
文档属性
| 名称 | 专题12 带电粒子在磁场中运动--2023高考物理分类解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 918.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-31 13:59:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023高考物理分类解析
专题12 带电粒子在磁场中运动
1. (2023高考全国乙卷) 如图,一磁感应强度大小为B的匀强磁场,方向垂直于纸面(xOy平面)向里,磁场右边界与x轴垂直。一带电粒子由O点沿x正向入射到磁场中,在磁场另一侧的S点射出,粒子离开磁场后,沿直线运动打在垂直于x轴的接收屏上的P点;SP = l,S与屏的距离为,与x轴的距离为a。如果保持所有条件不变,在磁场区域再加上电场强度大小为E的匀强电场,该粒子入射后则会沿x轴到达接收屏。该粒子的比荷为( )
A. B.
C. D.
【参考答案】A
【命题意图】本题考查带电粒子在磁场和复合场中的运动及其相关知识点。
【解题思路】设带电粒子电荷量q,质量为m,从O点沿x轴正方向射入磁场,画出运动轨迹,由图中几何关系可知偏转角θ为60°,由cosθ=解得r=2a。由洛伦兹力提供向心力,得qvB=m,在磁场区域加上电场,入射粒子沿x轴到达接受屏,qE=qvB,联立解得=,A正确。
【思路点拨】解答带电粒子在匀强磁场中运动问题,正确画出带电粒子运动轨迹是关键。
2. (2023高考全国甲卷)光滑刚性绝缘圆筒内存在着平行于轴的匀强磁场,筒上P点开有一个小孔,过P的横截面是以O为圆心的圆,如图所示。一带电粒子从P点沿PO方向射入,然后与筒壁发生碰撞。假设粒子每次碰撞前、后瞬间,速度沿圆上碰撞点的切线方向的分量大小不变,沿法线方向的分量大小不变,方向相反;电荷量不变,重力不计。下列说法正确的是
A. 粒子运动轨迹可能通过圆心,
B. 最少经2次碰撞,粒子就可能从小孔射出
C. 射入小孔时粒子的速度越大,在圆内运动时间越短
D. 每次碰撞后瞬间,粒子速度方向一定平行于碰撞点与圆心O的连线
【参考答案】BD
【命题意图】本题考查带电粒子在圆形区域匀强磁场中运动、洛伦兹力、牛顿运动定律及其相关知识点。
【解题思路】粒子沿PO射入,由于受到洛伦兹力作用,粒子运动轨迹不可能通过圆心,A错误;画出粒子运动轨迹,如图,可知粒子最少经2次碰撞,可能从小孔射出,B正确;射入小孔时速度越大,粒子做圆周运动的半径越大,碰撞次数会可能增多,粒子运动时间不一定减少, C错误;由题述和对称性可知,每次碰撞后瞬间,粒子速度方向一定平行于碰撞点与圆心O的连线,D正确。
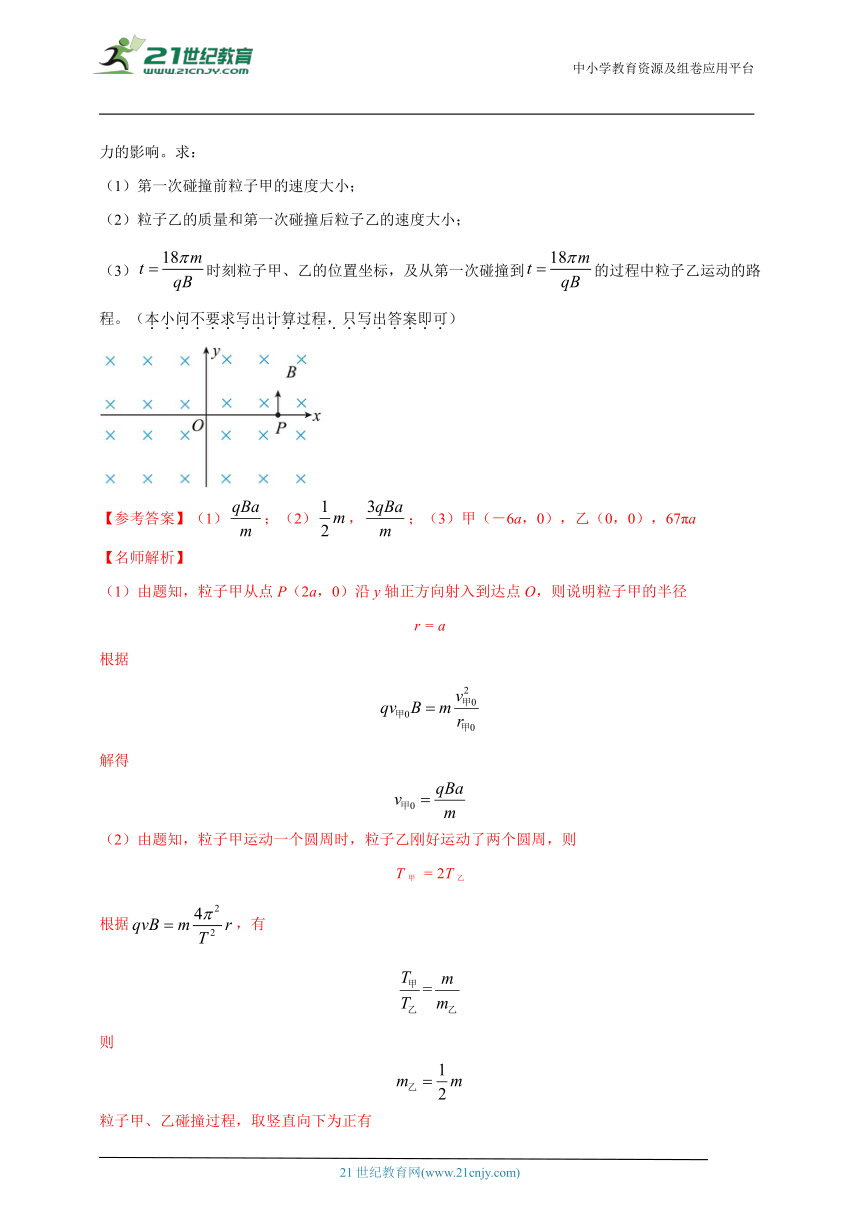
3. (2023高考湖北卷) 如图所示,空间存在磁感应强度大小为B、垂直于xOy平面向里的匀强磁场。t = 0时刻,一带正电粒子甲从点P(2a,0)沿y轴正方向射入,第一次到达点O时与运动到该点的带正电粒子乙发生正碰。碰撞后,粒子甲的速度方向反向、大小变为碰前的3倍,粒子甲运动一个圆周时,粒子乙刚好运动了两个圆周。己知粒子甲的质量为m,两粒子所带电荷量均为q。假设所有碰撞均为弹性正碰,碰撞时间忽略不计,碰撞过程中不发生电荷转移,不考虑重力和两粒子间库仑力的影响。求:
(1)第一次碰撞前粒子甲的速度大小;
(2)粒子乙的质量和第一次碰撞后粒子乙的速度大小;
(3)时刻粒子甲、乙的位置坐标,及从第一次碰撞到的过程中粒子乙运动的路程。(本小问不要求写出计算过程,只写出答案即可)
【参考答案】(1);(2),;(3)甲(-6a,0),乙(0,0),67πa
【名师解析】
(1)由题知,粒子甲从点P(2a,0)沿y轴正方向射入到达点O,则说明粒子甲的半径
r = a
根据
解得
(2)由题知,粒子甲运动一个圆周时,粒子乙刚好运动了两个圆周,则
T甲 = 2T乙
根据,有
则
粒子甲、乙碰撞过程,取竖直向下为正有
mv甲0+m乙v乙0= -mv甲1+m乙v乙1
解得
v乙0= -5v甲0,v乙1= 3v甲0
则第一次碰撞后粒子乙的速度大小为。
(3)已知在时,甲、乙粒子发生第一次碰撞且碰撞后有
v甲1= -3v甲0,v乙1= 3v甲0
则根据,可知此时乙粒子的运动半径为
可知在时,甲、乙粒子发生第二次碰撞,且甲、乙粒子发生第一次碰撞到第二次碰撞过程中乙粒子运动了2圈,此过程中乙粒子走过的路程为
S1= 6πa
且在第二次碰撞时有
mv甲1+m乙v乙1= mv甲2+m乙v乙2
解得
v甲2= v甲0,v乙2= -5v甲0
可知在时,甲、乙粒子发生第三次碰撞,且甲、乙粒子发生第二次碰撞到第三次碰撞过程中乙粒子运动了2圈,此过程中乙粒子走过的路程为
S2= 10πa
且在第三次碰撞时有
mv甲2+m乙v乙2= mv甲3+m乙v乙3
解得
v甲3= -3v甲0,v乙3= 3v甲0
依次类推
在时,甲、乙粒子发生第九次碰撞,且甲、乙粒子发生第八次碰撞到第九次碰撞过程中乙粒子运动了2圈,此过程中乙粒子走过的路程为
S8= 10πa
且在第九次碰撞时有
mv甲8+m乙v乙8= mv甲9+m乙v乙9
解得
v甲9=-3v甲0,v乙9= 3v甲0
在到过程中,甲粒子刚好运动半周,且甲粒子的运动半径为
r甲1 = 3a
则时甲粒子运动到P点即(-6a,0)处。
在到过程中,乙粒子刚好运动一周,则时乙粒子回到坐标原点,且此过程中乙粒子走过的路程为
S0 = 3πa
故整个过程中乙粒子走过总路程为
S = 4 × 6πa+4 × 10πa+3πa = 67πa
5.(11分)(2023年6月浙江高考选考)利用磁场实现离子偏转是科学仪器中广泛应用的技术。如图所示,Oxy平面(纸面)的第一象限内有足够长且宽度均为L、边界均平行x轴的区域Ⅰ和Ⅱ,其中区域存在磁感应强度大小为B1的匀强磁场,区域Ⅱ存在磁感应强度大小为B2的磁场,方向均垂直纸面向里,区域Ⅱ的下边界与x轴重合。位于处的离子源能释放出质量为m、电荷量为q、速度方向与x轴夹角为60°的正离子束,沿纸面射向磁场区域。不计离子的重力及离子间的相互作用,并忽略磁场的边界效应。
(1)求离子不进入区域Ⅱ的最大速度v1及其在磁场中的运动时间t;
(2)若,求能到达处的离子的最小速度v2;
(3)若,且离子源射出的离子数按速度大小均匀地分布在范围,求进入第四象限的离子数与总离子数之比η。
【名师解析】(1)画出离子恰不进入区域II的轨迹,由轨迹图中几何关系得
sin30°=,
解得r1=2L。
由洛伦兹力提供向心力,qv1B1=m,
解得v1=
运动轨迹所对圆心角为θ=2π/3
离子在区域II中运动时间t==
(2)解法一:常规法
画出离子恰好运动到y=L/2处的运动轨迹,如图。
速度为v2的离子在区域I,由洛伦兹力提供向心力,qv2B1=m,
解得r2=
速度为v2的离子在区域II,由洛伦兹力提供向心力,qv2B2=m,
解得r2’= == r2/2
在区域II,离子运动轨迹恰好与y=L/2水平线相切,r2’- r2’cosα=L/2,即r2- r2cosα=L,
解得:cosα=
在区域I,r2cosα-r2cos60°=L,即r2·-r2cos60°=L,
解得:r2=4L,
由= r2/2=2L,解得v2=
解法二:等效法。
若B2=2B1,由r=mv/qB
可知离子在区域I运动轨迹半径为r2=r’1/2,
可以等效为B2=B1时离子恰好运动到y=0处。
由图中几何关系可得:sin30°=,
解得r1’=4L。
离子在区域I磁场中运动,qv2B1=m,
解得v2=
解法三。动量定理+微元法
画出离子恰好运动到y=L/2处的运动轨迹,如图。我们可以通过微元法,利用动量定理解答。
对离子进入磁场到恰好运动到y=L/2处的过程,沿y轴方向的微元时间△t,运用动量定理,
-qB1vy1△t-qB2vy2△t =m△v
方程两侧求和,-qB1Σvy1△t-qB2Σvy2△t=mΣ△v
注意到Σvy1△t=L,Σvy2△t=0.5L,Σ△v=-v2sin30°
可得 -2qB1L=0.5m v2
解得:v2=
(3)解法一:等效法
画出B2=图像,如图。
区域II中磁场可等效为匀强磁场B1/2的匀强磁场,若把区域II中磁场等效为匀强磁场B1,则磁场宽度则为L/2。画出恰好能够进入第四象限的离子运动轨迹,如图。
由轨迹图中几何关系得
sin30°=,
解得r3=3L。
由洛伦兹力提供向心力,qv3B1=m,
解得v3=
即速度大于v3=的离子都能够进入第四象限,
进入第四象限的离子数与总离子数之比为
η=×100%=60%
解法二:动量定理+微元法
画出B2=图像,如图。
区域II中磁场可等效为匀强磁场B1/2的匀强磁场,
对离子进入磁场到恰好运动到x轴的过程,沿y轴方向的微元时间△t,运用动量定理,-qB1vy1△t-qB2vy2△t =m△v
方程两侧求和,-qB1Σvy1△t-qB2Σvy2△t=mΣ△v
注意到Σvy1△t=L,
ΣB2vy2△t=Σvy2△t =Σvy2△t =L,
Σ△v=-v2sin30°
可得 qB1L=m v2
解得:v3=
即速度大于v3=的离子都能够进入第四象限,
进入第四象限的离子数与总离子数之比为
η=×100%=60%
6. .(2023高考北京卷)如图所示,在磁感应强度大小为B、方向垂直纸面向外的匀强磁场中,固定一内部真空且内壁光滑的圆柱形薄壁绝缘管道,其轴线与磁场垂直.管道横截面半径为a,长度为l().带电粒子束持续以某一速度v沿轴线进入管道,粒子在磁场力作用下经过一段圆弧垂直打到管壁上,与管壁发生弹性碰撞,多次碰撞后从另一端射出,单位时间进入管道的粒子数为n,粒子电荷量为,不计粒子的重力、粒子间的相互作用,下列说法不正确的是( )
A.粒子在磁场中运动的圆弧半径为a
B.粒子质量为
C.管道内的等效电流为
D.粒子束对管道的平均作用力大小为
【参考答案】C
【名师解析】根据题述,带电粒子束持续以某一速度v沿轴线进入管道,粒子在磁场力作用下经过一段圆弧垂直打到管壁上,可知粒子在磁场中运动的圆弧半径为r=a,A正确;由洛伦兹力提供向心力,qvB=m,可得m=,B正确;由于带电粒子在管道内做匀速曲线运动,其定向移动的速度小于v,所以管道内的等效电流小于,C不正确;设△t时间与管道壁碰撞的带电粒子数为N,同一时间与管道壁碰撞的带电粒子数为N’=l/2a,对带电粒子与管道壁碰撞,由动量定理,F△t=NN’m·2v,N=n△t, m=,联立解得F=,D正确。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023高考物理分类解析
专题12 带电粒子在磁场中运动
1. (2023高考全国乙卷) 如图,一磁感应强度大小为B的匀强磁场,方向垂直于纸面(xOy平面)向里,磁场右边界与x轴垂直。一带电粒子由O点沿x正向入射到磁场中,在磁场另一侧的S点射出,粒子离开磁场后,沿直线运动打在垂直于x轴的接收屏上的P点;SP = l,S与屏的距离为,与x轴的距离为a。如果保持所有条件不变,在磁场区域再加上电场强度大小为E的匀强电场,该粒子入射后则会沿x轴到达接收屏。该粒子的比荷为( )
A. B.
C. D.
【参考答案】A
【命题意图】本题考查带电粒子在磁场和复合场中的运动及其相关知识点。
【解题思路】设带电粒子电荷量q,质量为m,从O点沿x轴正方向射入磁场,画出运动轨迹,由图中几何关系可知偏转角θ为60°,由cosθ=解得r=2a。由洛伦兹力提供向心力,得qvB=m,在磁场区域加上电场,入射粒子沿x轴到达接受屏,qE=qvB,联立解得=,A正确。
【思路点拨】解答带电粒子在匀强磁场中运动问题,正确画出带电粒子运动轨迹是关键。
2. (2023高考全国甲卷)光滑刚性绝缘圆筒内存在着平行于轴的匀强磁场,筒上P点开有一个小孔,过P的横截面是以O为圆心的圆,如图所示。一带电粒子从P点沿PO方向射入,然后与筒壁发生碰撞。假设粒子每次碰撞前、后瞬间,速度沿圆上碰撞点的切线方向的分量大小不变,沿法线方向的分量大小不变,方向相反;电荷量不变,重力不计。下列说法正确的是
A. 粒子运动轨迹可能通过圆心,
B. 最少经2次碰撞,粒子就可能从小孔射出
C. 射入小孔时粒子的速度越大,在圆内运动时间越短
D. 每次碰撞后瞬间,粒子速度方向一定平行于碰撞点与圆心O的连线
【参考答案】BD
【命题意图】本题考查带电粒子在圆形区域匀强磁场中运动、洛伦兹力、牛顿运动定律及其相关知识点。
【解题思路】粒子沿PO射入,由于受到洛伦兹力作用,粒子运动轨迹不可能通过圆心,A错误;画出粒子运动轨迹,如图,可知粒子最少经2次碰撞,可能从小孔射出,B正确;射入小孔时速度越大,粒子做圆周运动的半径越大,碰撞次数会可能增多,粒子运动时间不一定减少, C错误;由题述和对称性可知,每次碰撞后瞬间,粒子速度方向一定平行于碰撞点与圆心O的连线,D正确。
3. (2023高考湖北卷) 如图所示,空间存在磁感应强度大小为B、垂直于xOy平面向里的匀强磁场。t = 0时刻,一带正电粒子甲从点P(2a,0)沿y轴正方向射入,第一次到达点O时与运动到该点的带正电粒子乙发生正碰。碰撞后,粒子甲的速度方向反向、大小变为碰前的3倍,粒子甲运动一个圆周时,粒子乙刚好运动了两个圆周。己知粒子甲的质量为m,两粒子所带电荷量均为q。假设所有碰撞均为弹性正碰,碰撞时间忽略不计,碰撞过程中不发生电荷转移,不考虑重力和两粒子间库仑力的影响。求:
(1)第一次碰撞前粒子甲的速度大小;
(2)粒子乙的质量和第一次碰撞后粒子乙的速度大小;
(3)时刻粒子甲、乙的位置坐标,及从第一次碰撞到的过程中粒子乙运动的路程。(本小问不要求写出计算过程,只写出答案即可)
【参考答案】(1);(2),;(3)甲(-6a,0),乙(0,0),67πa
【名师解析】
(1)由题知,粒子甲从点P(2a,0)沿y轴正方向射入到达点O,则说明粒子甲的半径
r = a
根据
解得
(2)由题知,粒子甲运动一个圆周时,粒子乙刚好运动了两个圆周,则
T甲 = 2T乙
根据,有
则
粒子甲、乙碰撞过程,取竖直向下为正有
mv甲0+m乙v乙0= -mv甲1+m乙v乙1
解得
v乙0= -5v甲0,v乙1= 3v甲0
则第一次碰撞后粒子乙的速度大小为。
(3)已知在时,甲、乙粒子发生第一次碰撞且碰撞后有
v甲1= -3v甲0,v乙1= 3v甲0
则根据,可知此时乙粒子的运动半径为
可知在时,甲、乙粒子发生第二次碰撞,且甲、乙粒子发生第一次碰撞到第二次碰撞过程中乙粒子运动了2圈,此过程中乙粒子走过的路程为
S1= 6πa
且在第二次碰撞时有
mv甲1+m乙v乙1= mv甲2+m乙v乙2
解得
v甲2= v甲0,v乙2= -5v甲0
可知在时,甲、乙粒子发生第三次碰撞,且甲、乙粒子发生第二次碰撞到第三次碰撞过程中乙粒子运动了2圈,此过程中乙粒子走过的路程为
S2= 10πa
且在第三次碰撞时有
mv甲2+m乙v乙2= mv甲3+m乙v乙3
解得
v甲3= -3v甲0,v乙3= 3v甲0
依次类推
在时,甲、乙粒子发生第九次碰撞,且甲、乙粒子发生第八次碰撞到第九次碰撞过程中乙粒子运动了2圈,此过程中乙粒子走过的路程为
S8= 10πa
且在第九次碰撞时有
mv甲8+m乙v乙8= mv甲9+m乙v乙9
解得
v甲9=-3v甲0,v乙9= 3v甲0
在到过程中,甲粒子刚好运动半周,且甲粒子的运动半径为
r甲1 = 3a
则时甲粒子运动到P点即(-6a,0)处。
在到过程中,乙粒子刚好运动一周,则时乙粒子回到坐标原点,且此过程中乙粒子走过的路程为
S0 = 3πa
故整个过程中乙粒子走过总路程为
S = 4 × 6πa+4 × 10πa+3πa = 67πa
5.(11分)(2023年6月浙江高考选考)利用磁场实现离子偏转是科学仪器中广泛应用的技术。如图所示,Oxy平面(纸面)的第一象限内有足够长且宽度均为L、边界均平行x轴的区域Ⅰ和Ⅱ,其中区域存在磁感应强度大小为B1的匀强磁场,区域Ⅱ存在磁感应强度大小为B2的磁场,方向均垂直纸面向里,区域Ⅱ的下边界与x轴重合。位于处的离子源能释放出质量为m、电荷量为q、速度方向与x轴夹角为60°的正离子束,沿纸面射向磁场区域。不计离子的重力及离子间的相互作用,并忽略磁场的边界效应。
(1)求离子不进入区域Ⅱ的最大速度v1及其在磁场中的运动时间t;
(2)若,求能到达处的离子的最小速度v2;
(3)若,且离子源射出的离子数按速度大小均匀地分布在范围,求进入第四象限的离子数与总离子数之比η。
【名师解析】(1)画出离子恰不进入区域II的轨迹,由轨迹图中几何关系得
sin30°=,
解得r1=2L。
由洛伦兹力提供向心力,qv1B1=m,
解得v1=
运动轨迹所对圆心角为θ=2π/3
离子在区域II中运动时间t==
(2)解法一:常规法
画出离子恰好运动到y=L/2处的运动轨迹,如图。
速度为v2的离子在区域I,由洛伦兹力提供向心力,qv2B1=m,
解得r2=
速度为v2的离子在区域II,由洛伦兹力提供向心力,qv2B2=m,
解得r2’= == r2/2
在区域II,离子运动轨迹恰好与y=L/2水平线相切,r2’- r2’cosα=L/2,即r2- r2cosα=L,
解得:cosα=
在区域I,r2cosα-r2cos60°=L,即r2·-r2cos60°=L,
解得:r2=4L,
由= r2/2=2L,解得v2=
解法二:等效法。
若B2=2B1,由r=mv/qB
可知离子在区域I运动轨迹半径为r2=r’1/2,
可以等效为B2=B1时离子恰好运动到y=0处。
由图中几何关系可得:sin30°=,
解得r1’=4L。
离子在区域I磁场中运动,qv2B1=m,
解得v2=
解法三。动量定理+微元法
画出离子恰好运动到y=L/2处的运动轨迹,如图。我们可以通过微元法,利用动量定理解答。
对离子进入磁场到恰好运动到y=L/2处的过程,沿y轴方向的微元时间△t,运用动量定理,
-qB1vy1△t-qB2vy2△t =m△v
方程两侧求和,-qB1Σvy1△t-qB2Σvy2△t=mΣ△v
注意到Σvy1△t=L,Σvy2△t=0.5L,Σ△v=-v2sin30°
可得 -2qB1L=0.5m v2
解得:v2=
(3)解法一:等效法
画出B2=图像,如图。
区域II中磁场可等效为匀强磁场B1/2的匀强磁场,若把区域II中磁场等效为匀强磁场B1,则磁场宽度则为L/2。画出恰好能够进入第四象限的离子运动轨迹,如图。
由轨迹图中几何关系得
sin30°=,
解得r3=3L。
由洛伦兹力提供向心力,qv3B1=m,
解得v3=
即速度大于v3=的离子都能够进入第四象限,
进入第四象限的离子数与总离子数之比为
η=×100%=60%
解法二:动量定理+微元法
画出B2=图像,如图。
区域II中磁场可等效为匀强磁场B1/2的匀强磁场,
对离子进入磁场到恰好运动到x轴的过程,沿y轴方向的微元时间△t,运用动量定理,-qB1vy1△t-qB2vy2△t =m△v
方程两侧求和,-qB1Σvy1△t-qB2Σvy2△t=mΣ△v
注意到Σvy1△t=L,
ΣB2vy2△t=Σvy2△t =Σvy2△t =L,
Σ△v=-v2sin30°
可得 qB1L=m v2
解得:v3=
即速度大于v3=的离子都能够进入第四象限,
进入第四象限的离子数与总离子数之比为
η=×100%=60%
6. .(2023高考北京卷)如图所示,在磁感应强度大小为B、方向垂直纸面向外的匀强磁场中,固定一内部真空且内壁光滑的圆柱形薄壁绝缘管道,其轴线与磁场垂直.管道横截面半径为a,长度为l().带电粒子束持续以某一速度v沿轴线进入管道,粒子在磁场力作用下经过一段圆弧垂直打到管壁上,与管壁发生弹性碰撞,多次碰撞后从另一端射出,单位时间进入管道的粒子数为n,粒子电荷量为,不计粒子的重力、粒子间的相互作用,下列说法不正确的是( )
A.粒子在磁场中运动的圆弧半径为a
B.粒子质量为
C.管道内的等效电流为
D.粒子束对管道的平均作用力大小为
【参考答案】C
【名师解析】根据题述,带电粒子束持续以某一速度v沿轴线进入管道,粒子在磁场力作用下经过一段圆弧垂直打到管壁上,可知粒子在磁场中运动的圆弧半径为r=a,A正确;由洛伦兹力提供向心力,qvB=m,可得m=,B正确;由于带电粒子在管道内做匀速曲线运动,其定向移动的速度小于v,所以管道内的等效电流小于,C不正确;设△t时间与管道壁碰撞的带电粒子数为N,同一时间与管道壁碰撞的带电粒子数为N’=l/2a,对带电粒子与管道壁碰撞,由动量定理,F△t=NN’m·2v,N=n△t, m=,联立解得F=,D正确。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
