探索三角形全等(山西省大同市矿区)

课件17张PPT。《数学》( 北师大.七年级 下册 )第五章 三角形探索三角形全等的条件（1） 北师大?七年级《数学(下)》5 平川中学 许伟强
xwq0812@21cn.com问题引入：
小颖作业本上画的三角形被墨迹污染了，她想画一个与原来完全一样的三角形，她该怎么办？请你帮助小颖想一个办法，并说明你的理由？注意：与原来完全一样的三角形，即是与原来三角形全等的三角形。想一想：
要画一个三角形与小颖画的三角形全等。需要几个与边或角的大小有关的条件？只知道一个条件（一角或一边）行吗？两个条件呢？三个条件呢？让我们一起来探索三角形全等的条件做一做：
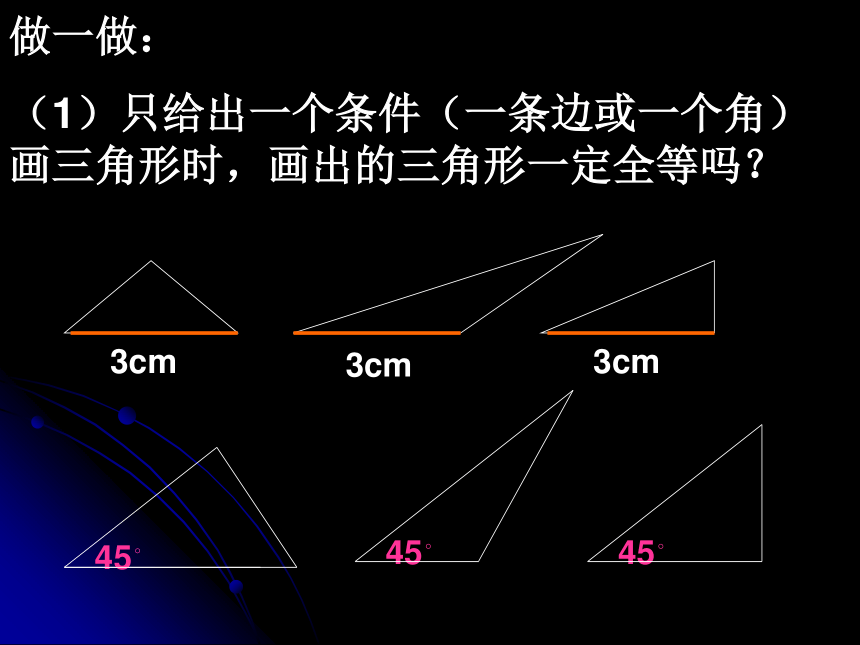
（1）只给出一个条件（一条边或一个角）画三角形时，画出的三角形一定全等吗？1)三角形的一个内角为30°，一条边为3cm;
2) 三角形的两个内角分别为30°和45°;
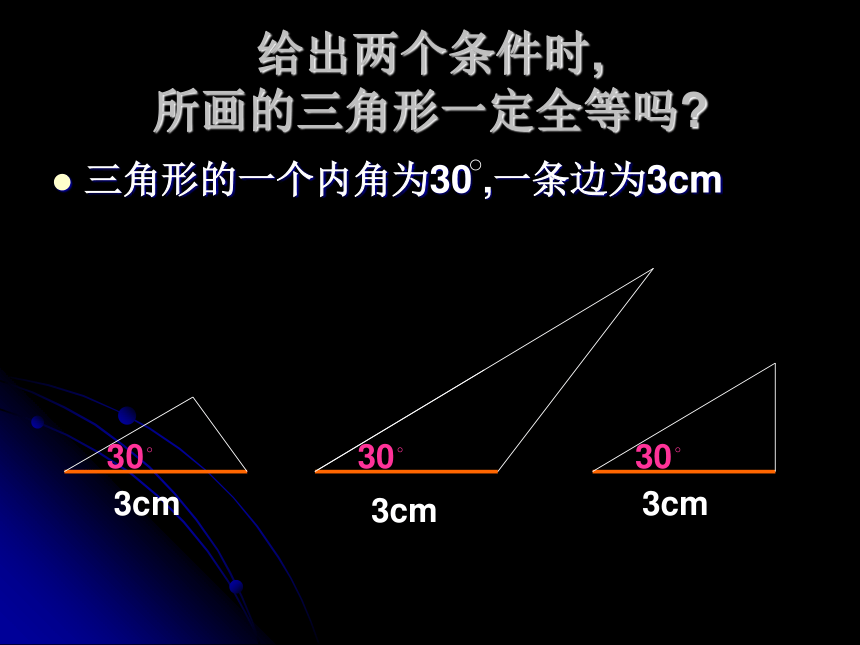
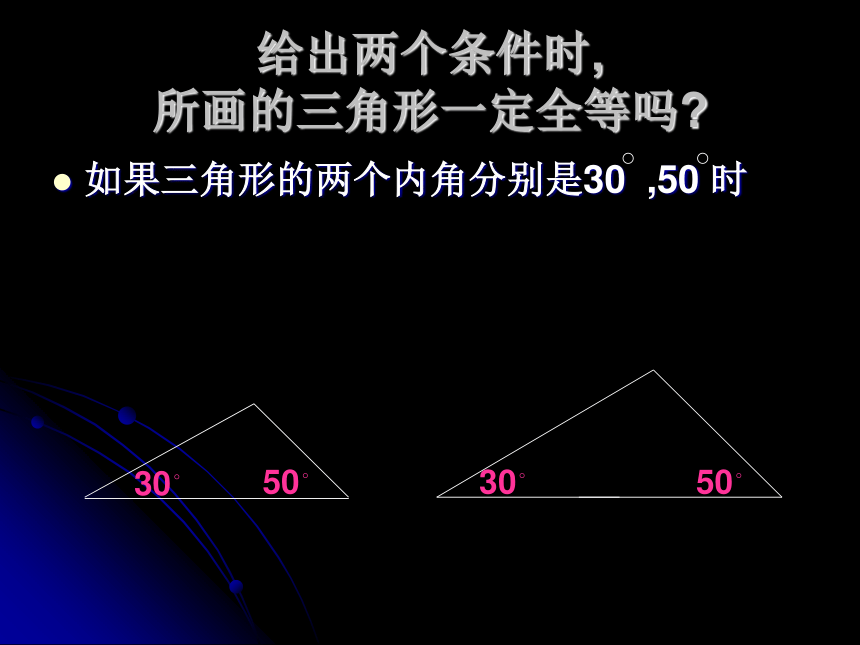
3）三角形的两条边分别为4cm和6cm.按下面的条件画三角形，画完后小组内交流，看所画的三角形是否全等。(其它条件不确定）（2）给出两个条件画三角形时，有几种可能的情况？每种情况下作出的三角形一定全等吗？三角形的一个内角为30 ,一条边为3cm30?给出两个条件时,所画的三角形一定全等吗?给出两个条件时,所画的三角形一定全等吗?如果三角形的两个内角分别是30 ,50 时30?30?50?50?给出两个条件时,所画的三角形一定全等吗?如果三角形的两边分别为4cm，6cm 时6cm6cm4cm4cm只给两个条件作出三角形，不能保正所画出的三角形一定全等。综上所述，只给出一个条件或两个条件时，都不能保证所画出的三角形一定全等。想一想：如果给出三个条件画三角形时，你能说出有哪几种可能的情况吗？有四种可能：三条边、三个角、两边一角和两角一边。做一做：1）与小组内的同学比较各自手中的三角尺，有没有三个内角对应相等的三角形，它们一定全等吗？和老师手中的三角板相比较呢？2）已知一个三角形的三条边分别为4cm、5cm、7cm，你能画出这个三角形吗？　　　　　看老师的作图示范，再画出这个三角形，并与同伴画的三角形进行比较？它 们一定全等吗？　　这说明有三个角对应相等的两个三角形不一定全等由此得出定理：三边对应相等的两个三角形全等，简写为“边边边”或“SSS”这个定理说明，只要三角形的三边的长度确定了，这个三角形的形状和大小就完全确定了，这也是三角形具有稳定性的原理。　当我们同时给四边形和三角形外力时，会发现四边形要变形，而三角形不变形。这就是三角形的特性－三角形的稳定性你能找出三角形的稳定性在生活中的应用吗？练习：1、如图，AB＝AC，BD＝CD，BH＝CH，图中有几组全等的三角形？它们全等的条件是什么？HDCBA解：有三组。　　　　　　　　在△ABH和△ACH中 ∵AB=AC，BH=CH，AH=AH　∴△ABH≌△ACH（SSS）；在△ABH和△ACH中∵AB=AC，BD=CD，AD=AD　∴△ABD≌△ACD（SSS）；在△ABH和△ACH中　　　　　　　　　　∵BD=CD，BH=CH，DH=DH∴△DBH≌△DCH（SSS）　练习2。如图，已知AB=CD，BC=DA。你能说明△ABC与△CDA全等吗？你能说明AB∥CD，AD∥BC吗？为什么？　DBAC解：在△ABC与△CDA中，
∵∴△ABC≌△CDA（SSS）
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等）　　∴AB∥CD，AD∥BC（内错角相等，两直线平行）小结：
　　今天我们经历了画图验证两个三角形全等的过程，探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”，我们可以利用它来判别两个三角形是否全等。
　　我们还知道了三角形具有稳定性，只要三角形的三边长度确定了，这个三角形的形状和大小就确定了。在生活　 中，三角形的稳定性有广泛的应用。作业：
P140页习题5.8第1、2、3题