4.3.1对数的概念 课件(共22张PPT)
文档属性
| 名称 | 4.3.1对数的概念 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 18:39:10 | ||
图片预览








文档简介
(共22张PPT)
第4章 指数函数与对数函数
4.3 对数
4.3.1 对数的概念
人教A版(2019)
教学目标
学习目标 数学素养
1.理解对数的概念,会用对数的定义进行对数式与指数式的互化. 1.数学抽象、数学运算素养.
2.知道自然对数和常用对数.
3.理解和掌握对数的性质,会求简单的对数值. 2.数学运算素养.
问题导入
在4.2.1的问题中,通过指数幂的运算,我们能从y=1.11x中求出经过x年后B地景区的游客人次为2001年的倍数y数.反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,…
这个问题实际上就是从2=1.11x,3=1.11x,4=1.11x,…,中分别求出x,即已知底数和幂的值求指数.这是解一个关于x的一元方程,本节课要学的就是怎么表达这个方程的解,即对数.
对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年).他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明.恩格斯把对数的发明与解析几何的创始,微积分的建立并称为17世纪数学的三大成就.
那么该如何解决?
?
新知导入
1.对数的概念
如果的次幂等于N,即>0且≠1),那么就称是以为底N的对数,记作.其中,叫做对数的底数,N叫做真数.
“log”是拉丁文logarithm(对数)的缩写.
对数的写法
上述问题情境中:由2=1.11x ,得x是以1.11为底2的对数,
记作
再如由25=32,得5是以2为底32的对数,记作
新知探究
这是因为
②N能小于或等于零吗?
(不能,这是因为a>0, ax=N >0)
结论: 对数式中真数要大于零.
(也就是说0和负数没有对数 !)
注意:①a>0 , 且a≠1;②0和负数没有对数 (真数大于0).
思考:在对数 (a>0 , 且a≠1)的概念中
①为什么限制a>0 , 且a≠1?
概念辨析
2.在对数式b=log(a-2)(5-a)中,实数a的取值范围是( )
A.{a|a>5或a<2 } B.{a|2C.{a|2C
对数有意义的两个条件:
①底数大于零且不等于1;
②对数的真数必须大于零.
新知探究
2.两个重要的对数:
⑴常用对数:
我们通常将以10为底的对数叫做常用对数(commonlogarithm). 为了简便,N的常用对数 简记作lgN.
例如:
简记作lg5;
简记作lg3.5.
⑵自然对数:
在科技、经济以及社会生活中常常使用以无理数e=2.71828……为底数的对数,以e为底的对数叫自然对数(naturallogarithm).为了简便,N的自然对数 简记作lnN.
例如:
简记作ln3 ;
简记作ln10
新知探究
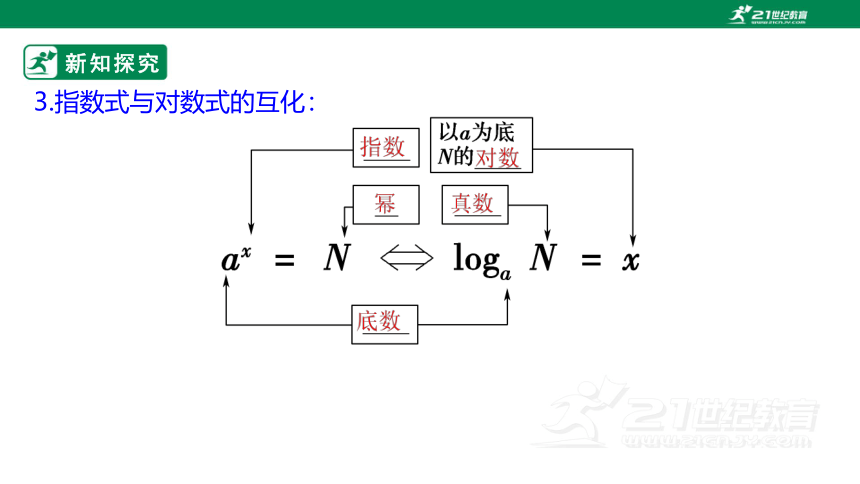
3.指数式与对数式的互化:
新知讲解
【例1】将下列指数式化为对数式,对数式化为指数式:
(1)54=625; (2) ; (3) ;
(4) ; (5)lg0.01=-2; (6)ln10=2.303.
解:
(1)log5625=4;
(2) ;
(3) ;
(4) ;
(5)10-2=0.01;
(6)e2.303=10.
注意:①本题运用“当a>0且a≠1时,;
②第⑸题的底数是10,第⑹题的底数是e.
初试身手
1.把下列指数式写成对数式,对数式写成指数式:
(1) 23=8; (2) ; (3) .
(4) log39=2; (5) lgn=2.3; (6) log3 =-4.
解:(1) log28 = 3;
(2) lnm= ;
(3) ;
(4) 32=9;
(5) 102.3=n;
(6) 3-4= .
ax =N logaN = x
新知讲解
【例2】求下列各式中的x的值:
(1); (2);
(3); (4).
解:
(1)因为,
所以 ,
(3)∵,
(2)∵
则x=2.
(4)∵,
=
,
=
,
,
则x=-2.
初试身手
解析:
⑶∵,∴,
∴x=-5.
⑴∵,∴x==27;
2.求下列各式中x的值:
(1) ; (2) logx49 = 4;
(3) lg0.00001=x; (4) ln = -x.
⑵∵4,∴=49,=7,
又∵x>0,∴x=.
⑷∵,∴,
∴x=-.
新知探究
3.对数的基本性质
①;
②.
【例3】求下列各式中x的值:
⑴=0; ⑵ =1.
解:
⑴∵,∴,
∴x=5.
⑵∵,∴=3,
∴x==1000.
初试身手
解:
(1)∵lg(ln x)=1,∴ln x=10,
∴x=e10.
(2)∵lg(ln x)=0, ∴ln x=1,
∴x=e.
3.求下列各式中x的值.
(1)lg(ln x)=1; (2)lg(ln x)=0.
新知探究
探究:恒等式:.
证明:设,则,
所以x=N,
即=N.
新知形成
【例4】 ⑴式子= ;
⑵若=25,则x的值等于( )
A.10 B.13 C.100 D.±100
⑶式子的值为 .
解:
⑵∵=25,
⑴
∴2x-1=25,x=13.
⑶= .
=.
B
初试身手
4.求下列各式的值:
⑴ ; ⑵.
解:
AC
⑴=4.
⑵=5×2=10.
课堂小结
1.对数的定义
一般地, 如果ax=N(a>0, 且a≠1), 那么数x叫做以a为底N的对数(logarithm), 记作 其中a叫做对数的底数, N叫做真数.
x = logaN ,
2.两种特殊的对数
(1)以10为底的对数叫常用对数, 并把log10N记作lgN.
(2)以无理数e为底的对数叫自然对数并把logeN记作lnN.
3.对数与指数之间的关系
ax =N logaN = x
4.对数的基本性质
注意:0和负数没有对数;
①;
②.
5.对数恒等式:
.
作业布置
作业:p126-127. 习题4.3 1,2⑴.
补充题:
1.在M=log(x-3)(x+1)中,要使式子有意义,则x的取值范围为
A.(-∞,3] B.(3,4)∪(4,+∞)
C.(4,+∞) D.(3,4)
2.若=0,则x= .
3.= .
4.求下列各式中x的值:
(1) ;
(2) log2[log3(log4x)]=0.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第4章 指数函数与对数函数
4.3 对数
4.3.1 对数的概念
人教A版(2019)
教学目标
学习目标 数学素养
1.理解对数的概念,会用对数的定义进行对数式与指数式的互化. 1.数学抽象、数学运算素养.
2.知道自然对数和常用对数.
3.理解和掌握对数的性质,会求简单的对数值. 2.数学运算素养.
问题导入
在4.2.1的问题中,通过指数幂的运算,我们能从y=1.11x中求出经过x年后B地景区的游客人次为2001年的倍数y数.反之,如果要求经过多少年游客人次是2001年的2倍,3倍,4倍,…
这个问题实际上就是从2=1.11x,3=1.11x,4=1.11x,…,中分别求出x,即已知底数和幂的值求指数.这是解一个关于x的一元方程,本节课要学的就是怎么表达这个方程的解,即对数.
对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年).他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明.恩格斯把对数的发明与解析几何的创始,微积分的建立并称为17世纪数学的三大成就.
那么该如何解决?
?
新知导入
1.对数的概念
如果的次幂等于N,即>0且≠1),那么就称是以为底N的对数,记作.其中,叫做对数的底数,N叫做真数.
“log”是拉丁文logarithm(对数)的缩写.
对数的写法
上述问题情境中:由2=1.11x ,得x是以1.11为底2的对数,
记作
再如由25=32,得5是以2为底32的对数,记作
新知探究
这是因为
②N能小于或等于零吗?
(不能,这是因为a>0, ax=N >0)
结论: 对数式中真数要大于零.
(也就是说0和负数没有对数 !)
注意:①a>0 , 且a≠1;②0和负数没有对数 (真数大于0).
思考:在对数 (a>0 , 且a≠1)的概念中
①为什么限制a>0 , 且a≠1?
概念辨析
2.在对数式b=log(a-2)(5-a)中,实数a的取值范围是( )
A.{a|a>5或a<2 } B.{a|2
对数有意义的两个条件:
①底数大于零且不等于1;
②对数的真数必须大于零.
新知探究
2.两个重要的对数:
⑴常用对数:
我们通常将以10为底的对数叫做常用对数(commonlogarithm). 为了简便,N的常用对数 简记作lgN.
例如:
简记作lg5;
简记作lg3.5.
⑵自然对数:
在科技、经济以及社会生活中常常使用以无理数e=2.71828……为底数的对数,以e为底的对数叫自然对数(naturallogarithm).为了简便,N的自然对数 简记作lnN.
例如:
简记作ln3 ;
简记作ln10
新知探究
3.指数式与对数式的互化:
新知讲解
【例1】将下列指数式化为对数式,对数式化为指数式:
(1)54=625; (2) ; (3) ;
(4) ; (5)lg0.01=-2; (6)ln10=2.303.
解:
(1)log5625=4;
(2) ;
(3) ;
(4) ;
(5)10-2=0.01;
(6)e2.303=10.
注意:①本题运用“当a>0且a≠1时,;
②第⑸题的底数是10,第⑹题的底数是e.
初试身手
1.把下列指数式写成对数式,对数式写成指数式:
(1) 23=8; (2) ; (3) .
(4) log39=2; (5) lgn=2.3; (6) log3 =-4.
解:(1) log28 = 3;
(2) lnm= ;
(3) ;
(4) 32=9;
(5) 102.3=n;
(6) 3-4= .
ax =N logaN = x
新知讲解
【例2】求下列各式中的x的值:
(1); (2);
(3); (4).
解:
(1)因为,
所以 ,
(3)∵,
(2)∵
则x=2.
(4)∵,
=
,
=
,
,
则x=-2.
初试身手
解析:
⑶∵,∴,
∴x=-5.
⑴∵,∴x==27;
2.求下列各式中x的值:
(1) ; (2) logx49 = 4;
(3) lg0.00001=x; (4) ln = -x.
⑵∵4,∴=49,=7,
又∵x>0,∴x=.
⑷∵,∴,
∴x=-.
新知探究
3.对数的基本性质
①;
②.
【例3】求下列各式中x的值:
⑴=0; ⑵ =1.
解:
⑴∵,∴,
∴x=5.
⑵∵,∴=3,
∴x==1000.
初试身手
解:
(1)∵lg(ln x)=1,∴ln x=10,
∴x=e10.
(2)∵lg(ln x)=0, ∴ln x=1,
∴x=e.
3.求下列各式中x的值.
(1)lg(ln x)=1; (2)lg(ln x)=0.
新知探究
探究:恒等式:.
证明:设,则,
所以x=N,
即=N.
新知形成
【例4】 ⑴式子= ;
⑵若=25,则x的值等于( )
A.10 B.13 C.100 D.±100
⑶式子的值为 .
解:
⑵∵=25,
⑴
∴2x-1=25,x=13.
⑶= .
=.
B
初试身手
4.求下列各式的值:
⑴ ; ⑵.
解:
AC
⑴=4.
⑵=5×2=10.
课堂小结
1.对数的定义
一般地, 如果ax=N(a>0, 且a≠1), 那么数x叫做以a为底N的对数(logarithm), 记作 其中a叫做对数的底数, N叫做真数.
x = logaN ,
2.两种特殊的对数
(1)以10为底的对数叫常用对数, 并把log10N记作lgN.
(2)以无理数e为底的对数叫自然对数并把logeN记作lnN.
3.对数与指数之间的关系
ax =N logaN = x
4.对数的基本性质
注意:0和负数没有对数;
①;
②.
5.对数恒等式:
.
作业布置
作业:p126-127. 习题4.3 1,2⑴.
补充题:
1.在M=log(x-3)(x+1)中,要使式子有意义,则x的取值范围为
A.(-∞,3] B.(3,4)∪(4,+∞)
C.(4,+∞) D.(3,4)
2.若=0,则x= .
3.= .
4.求下列各式中x的值:
(1) ;
(2) log2[log3(log4x)]=0.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
