数学人教A版(2019)必修第一册第三章函数的概念与性质章末复习(共36张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册第三章函数的概念与性质章末复习(共36张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 00:00:00 | ||
图片预览







文档简介
(共36张PPT)
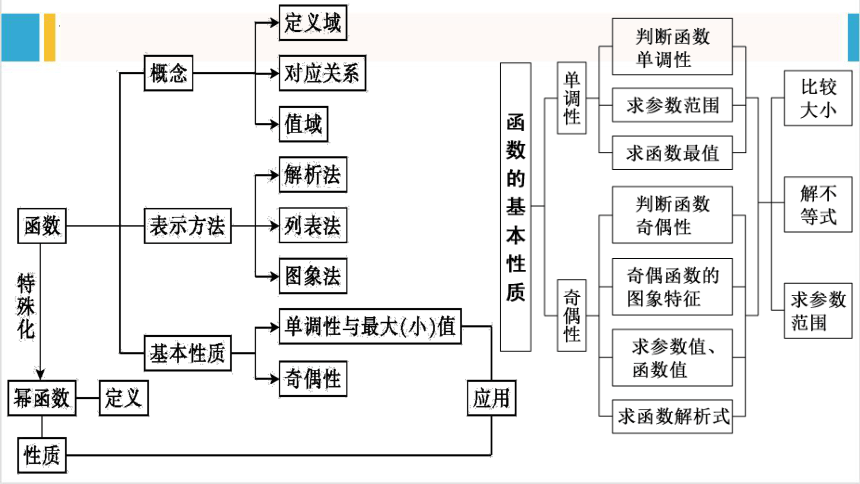
第三章章末复习
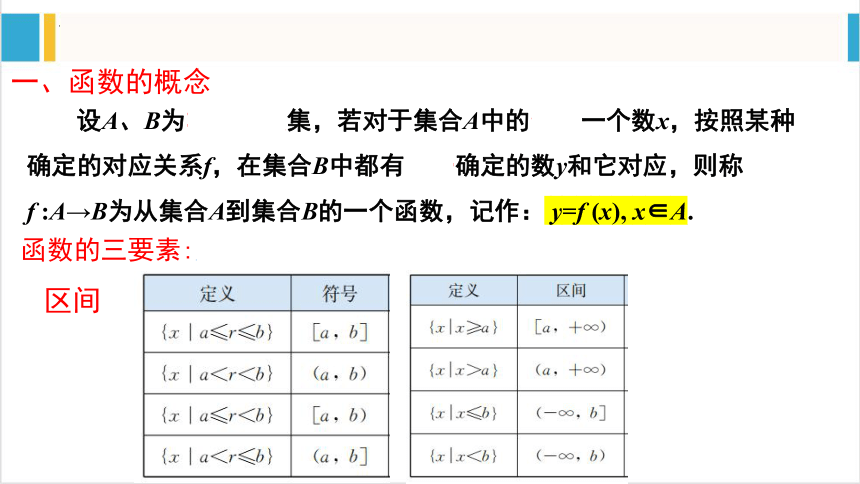
设A、B为非空实数集,若对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,则称 f :A→B为从集合A到集合B的一个函数,记作: y=f (x), x∈A.
一、函数的概念
函数的三要素:定义域,对应关系f,值域
区间
一般地,设函数:
如果,当时,都有,那么就称函数在区间上单调递增.其中叫做函数的单调递增区间,简称增区间.
如果,当时,都有,那么就称函数在区间上单调递减.其中叫做函数的单调递减区间,简称减区间.
函数在区间上具有单调性,叫做函数的一个单调区间
二、函数的单调性
(1)图象法
(2)定义法: 步骤:取值、作差、化简、判号、下结论
(3)性质法:增+增=增;减+减=减;
增-减=增;减-增=减;
(4)复合函数:“同增异减”原则.
判断函数的单调性
2、奇函数:设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。图象关于原点对称
1、偶函数: 设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。图象关于轴对称
三、函数的奇偶性
1、定义法
①确定定义域,并观察定义域是否关于原点对称.
②计算,并比较与的关系.
③若,则为奇函数,其图像关于原点对称;
若,则为偶函数,其图像关于y轴对称.
2、图象法(对称)
3、性质法(不研究的情况)
①奇奇=奇;偶偶=偶;②奇奇=偶;奇偶=奇;偶偶=偶;
判断函数的奇偶性
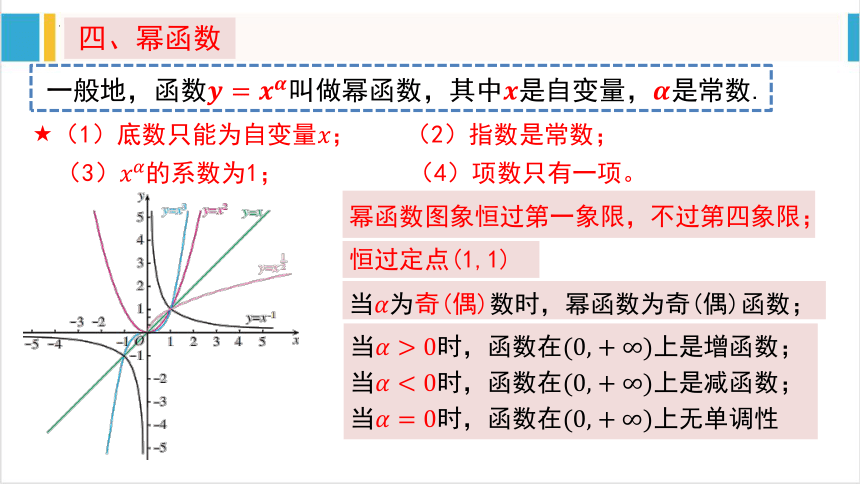
四、幂函数
一般地,函数叫做幂函数,其中是自变量,是常数.
(1)底数只能为自变量; (2)指数是常数;
(3)的系数为1; (4)项数只有一项。
幂函数图象恒过第一象限,不过第四象限;
恒过定点(1,1)
当为奇(偶)数时,幂函数为奇(偶)函数;
当时,函数在上是增函数;
当时,函数在上是减函数;
当时,函数在上无单调性
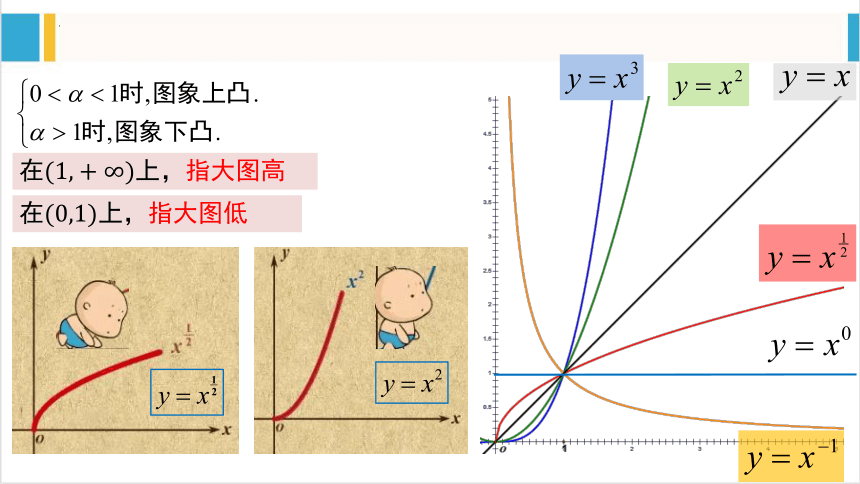
在上,指大图高
在上,指大图低
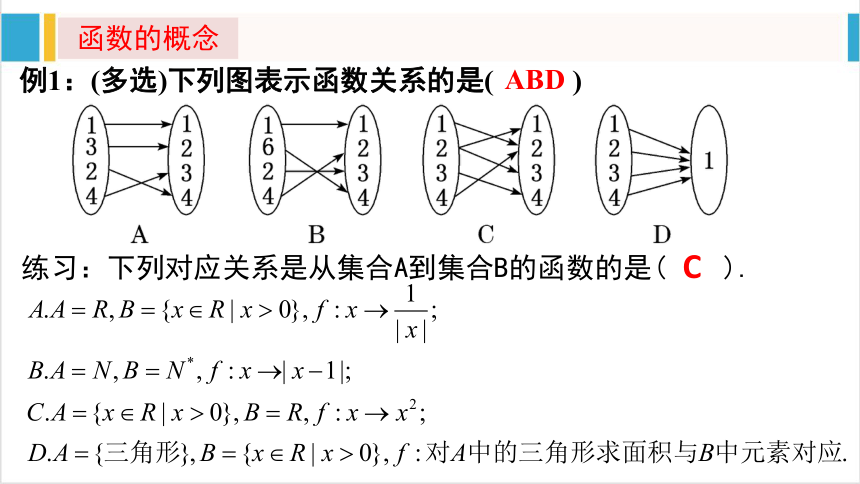
例1:(多选)下列图表示函数关系的是( )
ABD
练习:下列对应关系是从集合A到集合B的函数的是( ).
C
函数的概念
C
C
C
课前预学
课堂导学
分段函数
B
A
1、函数的定义域为_________________.
求函数定义域
例题:求下列函数的值域
(1)f(x)=x2-4x+5 (x∈[0 , 5]);
(4)f(x)=
求函数值域(最值)
[1,10]
高考演练
练习:求下列函数的解析式:
(1)已知幂函数f(x)的图象过点,求f(x)的解析式.
求函数解析式
CD
单调增区间:(-∞,-2]和(-2,+∞)
无单调减区间
2、求函数的单调区间.
判断函数的单调性
3、已知函数f(x)=x2+ax+b.若函数f(x)在区间[1,2]上不单调,则实数a的取值范围为_____________.
将“不单调”改为“具有单调性”
2、若f(x)=(m-1)x+b在R上是增函数,则f(m)与f(1)的大小关系是 ( )
A.f(m)f(1) C.f(m)≤f(1) D.f(m)≥f(1)
B
函数单调性的应用
4、0.23-2.3与0.24-2.3的大小关系是________________.
0.23-2.3>0.24-2.3
1、已知函数y=f(x)是定义在(-2,3)上的增函数,且f(2m-1)>f(-m),则实数m的取值范围是( )
A
(-4,-2)
函数单调性的应用
7、函数上单调递增,则的取值范围是_________.
1、下列判断不正确的是__________.
①④
是奇函数
3、已知是定义在上的奇函数,则_____________.
2
函数的奇偶性
2、判断并证明的奇偶性.
偶函数
A
函数的奇偶性
5、若f(x)和g(x)都是奇函数,且F(x)=f(x)+g(x)+2在(0,+∞)上有最大值8,则在(-∞,0)上F(x)有( )
A.最小值-8 B.最大值-8 C.最小值-6 D.最小值-4
D
解析:根据题意有f(x)+g(x)在(0,+∞)上有最大值6,
又因为f(x)和g(x)都是奇函数,所以f(x)+g(x)是奇函数且f(x)+g(x)在(-∞,0)上有最小值-6,则F(x)在(-∞,0)上有最小值-6+2=-4.故选D.
幂函数
B
C
3.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a>b>d>c
B
1、已知定义在R上的函数的图象是连续不断的,且满足以下条件:①;①,当时,都有;③,则下列选项成立的是( ).
A. B.若,则
C.若,则 D.,使得
CD
单调性与奇偶性的应用
2、已知函数,,若至少存在一个实数使得
成立,则的取值范围是________________.
3、已知函数的定义域为,且满足条件:①;②;③当时,
(1)判断函数的奇偶性并证明;
(2)判断函数的单调性并证明;
(3)求不等式的解集.
(2023年全国I卷)已知函数的定义域为,,则下列说法正确的是___________________.
① ② ③是偶函数
抽象函数的性质
①②③
练习:定义在上的函数满足:①;
②;③
(1)判断函数的奇偶性并证明;
(2)若恒成立,求实数的取值范围.
1、已知定义域为R的函数f(x)在[1,+∞)上单调递增,且f(x+1)为偶函数,若f(3)=1,则不等式f(2x+1)<1的解集为( )
A.(-1,1) B.(-1,+∞) C.(-∞,1) D.(-∞,-1)∪(1,+∞)
A
0
3、设定义在R上的函数f(x)满足f(x+1)=—f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2 023)=________.
1 012
对称性与周期性
练习:已知f(x)是定义在R上的奇函数,且f(2)=0,若对任意x∈R,都有f(x+4)=f(x)+f(4)成立,则f(2 022)的值为( )
A.2 022 B.2 020 C.2 018 D.0
D
解析:因为f(x)是定义在R上的奇函数,且f(-2)=-f(2)=0,f(x+4)=f(x)+f(4),所以f(2)=f(-2+4)=f(-2)+f(4),所以f(4)=0,所以f(x+4)=f(x),即f(x)的周期为4,所以f(2 022)=f(2)=0.故选D.
1、已知f(x)是R上的奇函数,且f(2-x)=f(x),f(1)=3,则
f(2 022)+f(2 023)的值为( )
A.-3 B.-1 C.1 D.2
B
解析:由题意,函数f(x)为R上的奇函数,可得f(2+x)=f(-x)=-f(x),所以f(x+4)=f(x),所以f(x)是周期为4的周期函数,所以f(2 022)+f(2 023)=f(2)+f(-1),因为f(-x+1)=f(x+1),令x=1,得f(0)=f(2),因为f(x)为R上的奇函数,所以f(0)=0,f(-1)=-f(1)=-3,所以f(2 022)+f(2 023)=0-3=-3.故选A.
函数性质的综合应用
链接高考
D
练习:某市有A,B两家羽毛球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内(含20小时)每块场地收费90元,超过20小时的部分,每块场地每小时2元.某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
(1)设在A俱乐部租一块场地开展活动x小时的收费为f(x)元(12≤x≤30),在B俱乐部租一块场地开展活动x小时的收费为g(x)元(12≤x≤30),试求f(x)与g(x)的解析式;
(2)问该企业选择哪家俱乐部比较合算,为什么?
实际应用
②当20<x≤30时,f(x)>g(x).
综上,当12≤x<15时,选A俱乐部合算;
当x=15时,选A,B俱乐部都合算;
当15<x≤30时,选B俱乐部合算.
ABD
AD
第三章章末复习
设A、B为非空实数集,若对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,则称 f :A→B为从集合A到集合B的一个函数,记作: y=f (x), x∈A.
一、函数的概念
函数的三要素:定义域,对应关系f,值域
区间
一般地,设函数:
如果,当时,都有,那么就称函数在区间上单调递增.其中叫做函数的单调递增区间,简称增区间.
如果,当时,都有,那么就称函数在区间上单调递减.其中叫做函数的单调递减区间,简称减区间.
函数在区间上具有单调性,叫做函数的一个单调区间
二、函数的单调性
(1)图象法
(2)定义法: 步骤:取值、作差、化简、判号、下结论
(3)性质法:增+增=增;减+减=减;
增-减=增;减-增=减;
(4)复合函数:“同增异减”原则.
判断函数的单调性
2、奇函数:设函数的定义域为 ,如果,都有,且,那么函数就叫做奇函数。图象关于原点对称
1、偶函数: 设函数的定义域为 ,如果,都有,且,那么函数就叫做偶函数。图象关于轴对称
三、函数的奇偶性
1、定义法
①确定定义域,并观察定义域是否关于原点对称.
②计算,并比较与的关系.
③若,则为奇函数,其图像关于原点对称;
若,则为偶函数,其图像关于y轴对称.
2、图象法(对称)
3、性质法(不研究的情况)
①奇奇=奇;偶偶=偶;②奇奇=偶;奇偶=奇;偶偶=偶;
判断函数的奇偶性
四、幂函数
一般地,函数叫做幂函数,其中是自变量,是常数.
(1)底数只能为自变量; (2)指数是常数;
(3)的系数为1; (4)项数只有一项。
幂函数图象恒过第一象限,不过第四象限;
恒过定点(1,1)
当为奇(偶)数时,幂函数为奇(偶)函数;
当时,函数在上是增函数;
当时,函数在上是减函数;
当时,函数在上无单调性
在上,指大图高
在上,指大图低
例1:(多选)下列图表示函数关系的是( )
ABD
练习:下列对应关系是从集合A到集合B的函数的是( ).
C
函数的概念
C
C
C
课前预学
课堂导学
分段函数
B
A
1、函数的定义域为_________________.
求函数定义域
例题:求下列函数的值域
(1)f(x)=x2-4x+5 (x∈[0 , 5]);
(4)f(x)=
求函数值域(最值)
[1,10]
高考演练
练习:求下列函数的解析式:
(1)已知幂函数f(x)的图象过点,求f(x)的解析式.
求函数解析式
CD
单调增区间:(-∞,-2]和(-2,+∞)
无单调减区间
2、求函数的单调区间.
判断函数的单调性
3、已知函数f(x)=x2+ax+b.若函数f(x)在区间[1,2]上不单调,则实数a的取值范围为_____________.
将“不单调”改为“具有单调性”
2、若f(x)=(m-1)x+b在R上是增函数,则f(m)与f(1)的大小关系是 ( )
A.f(m)
B
函数单调性的应用
4、0.23-2.3与0.24-2.3的大小关系是________________.
0.23-2.3>0.24-2.3
1、已知函数y=f(x)是定义在(-2,3)上的增函数,且f(2m-1)>f(-m),则实数m的取值范围是( )
A
(-4,-2)
函数单调性的应用
7、函数上单调递增,则的取值范围是_________.
1、下列判断不正确的是__________.
①④
是奇函数
3、已知是定义在上的奇函数,则_____________.
2
函数的奇偶性
2、判断并证明的奇偶性.
偶函数
A
函数的奇偶性
5、若f(x)和g(x)都是奇函数,且F(x)=f(x)+g(x)+2在(0,+∞)上有最大值8,则在(-∞,0)上F(x)有( )
A.最小值-8 B.最大值-8 C.最小值-6 D.最小值-4
D
解析:根据题意有f(x)+g(x)在(0,+∞)上有最大值6,
又因为f(x)和g(x)都是奇函数,所以f(x)+g(x)是奇函数且f(x)+g(x)在(-∞,0)上有最小值-6,则F(x)在(-∞,0)上有最小值-6+2=-4.故选D.
幂函数
B
C
3.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的大小关系是( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a>b>d>c
B
1、已知定义在R上的函数的图象是连续不断的,且满足以下条件:①;①,当时,都有;③,则下列选项成立的是( ).
A. B.若,则
C.若,则 D.,使得
CD
单调性与奇偶性的应用
2、已知函数,,若至少存在一个实数使得
成立,则的取值范围是________________.
3、已知函数的定义域为,且满足条件:①;②;③当时,
(1)判断函数的奇偶性并证明;
(2)判断函数的单调性并证明;
(3)求不等式的解集.
(2023年全国I卷)已知函数的定义域为,,则下列说法正确的是___________________.
① ② ③是偶函数
抽象函数的性质
①②③
练习:定义在上的函数满足:①;
②;③
(1)判断函数的奇偶性并证明;
(2)若恒成立,求实数的取值范围.
1、已知定义域为R的函数f(x)在[1,+∞)上单调递增,且f(x+1)为偶函数,若f(3)=1,则不等式f(2x+1)<1的解集为( )
A.(-1,1) B.(-1,+∞) C.(-∞,1) D.(-∞,-1)∪(1,+∞)
A
0
3、设定义在R上的函数f(x)满足f(x+1)=—f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2 023)=________.
1 012
对称性与周期性
练习:已知f(x)是定义在R上的奇函数,且f(2)=0,若对任意x∈R,都有f(x+4)=f(x)+f(4)成立,则f(2 022)的值为( )
A.2 022 B.2 020 C.2 018 D.0
D
解析:因为f(x)是定义在R上的奇函数,且f(-2)=-f(2)=0,f(x+4)=f(x)+f(4),所以f(2)=f(-2+4)=f(-2)+f(4),所以f(4)=0,所以f(x+4)=f(x),即f(x)的周期为4,所以f(2 022)=f(2)=0.故选D.
1、已知f(x)是R上的奇函数,且f(2-x)=f(x),f(1)=3,则
f(2 022)+f(2 023)的值为( )
A.-3 B.-1 C.1 D.2
B
解析:由题意,函数f(x)为R上的奇函数,可得f(2+x)=f(-x)=-f(x),所以f(x+4)=f(x),所以f(x)是周期为4的周期函数,所以f(2 022)+f(2 023)=f(2)+f(-1),因为f(-x+1)=f(x+1),令x=1,得f(0)=f(2),因为f(x)为R上的奇函数,所以f(0)=0,f(-1)=-f(1)=-3,所以f(2 022)+f(2 023)=0-3=-3.故选A.
函数性质的综合应用
链接高考
D
练习:某市有A,B两家羽毛球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内(含20小时)每块场地收费90元,超过20小时的部分,每块场地每小时2元.某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
(1)设在A俱乐部租一块场地开展活动x小时的收费为f(x)元(12≤x≤30),在B俱乐部租一块场地开展活动x小时的收费为g(x)元(12≤x≤30),试求f(x)与g(x)的解析式;
(2)问该企业选择哪家俱乐部比较合算,为什么?
实际应用
②当20<x≤30时,f(x)>g(x).
综上,当12≤x<15时,选A俱乐部合算;
当x=15时,选A,B俱乐部都合算;
当15<x≤30时,选B俱乐部合算.
ABD
AD
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
