专题6.1平方根 知识讲解(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题6.1平方根 知识讲解(含解析)2023-2024学年七年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 511.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 18:46:15 | ||
图片预览




文档简介
专题6.1 平方根(知识讲解)
【学习目标】
1.了解平方根、算术平方根的概念,会用根号表示数的平方根.
2.了解开方与乘方互为逆运算,会用开方运算求某些非负数的平方根,会用计算器求平方根.
【要点梳理】
知识点一、平方根和算术平方根的概念
1.算术平方根的定义
如果一个正数的平方等于,即,那么这个正数叫做的算术平方根(规定0的算术平方根还是0);的算术平方根记作,读作“的算术平方根”,叫做被开方数.
特别说明:当式子有意义时,一定表示一个非负数,即≥0,≥0.
2.平方根的定义
如果,那么叫做的平方根.求一个数的平方根的运算,叫做开平方.平方与开平方互为逆运算. (≥0)的平方根的符号表达为,其中是的算术平方根.
知识点二、平方根和算术平方根的区别与联系
1.区别:(1)定义不同;(2)结果不同:和
2.联系:(1)平方根包含算术平方根;
(2)被开方数都是非负数;
(3)0的平方根和算术平方根均为0.
特别说明:(1)正数的平方根有两个,它们互为相反数,其中正的那个叫它的算术平方根;负数没有平方根.
(2)正数的两个平方根互为相反数,根据它的算术平方根可以立即写出它的另一个平方根.因此,我们可以利用算术平方根来研究平方根.
知识点三、平方根的性质
知识点四、平方根小数点位数移动规律
被开方数的小数点向右或者向左移动2位,它的算术平方根的小数点就相应地向右或者向左移动1位.例如:,,,.
【典型例题】
类型一、平方根 概念的理解 平方根 算术平方根
1.
1.下列说法:①的平方根是±0.5;②任何数的平方都是非负数,因而任何数的平方根也是非负数;③算术平方根等于它本身的数是0,1;④平方根等于本身的数是0,其中正确的是( )
A.④ B.①② C.②③④ D.③④
举一反三:
【变式1】
2.下列说法中正确的是( )
A.的平方根为 B.的算术平方根为
C.0的平方根与算术平方根都是0 D.的平方根为
【变式2】
3.下列说法:(1)任何一个数都有两个平方根,它们互为相反数;(2)数a的平方根是±;(3)的算术平方根是2;(4)负数不能开平方; (5),其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
类型二、平方根 求一个数的平方根与算术平方根
2.
4.若是的算术平方根,则的平方根是 .
举一反三:
【变式1】
5.0.16的算术平方根是 ,的平方根是 .
【变式2】
6.已知2a-1的算术平方根为3,3a+b-1的算术平方根为4,求a+2的平方根.
类型三、平方根 平方根 算术平方根的非负性
3.
7.已知=b+8,求a+b的平方根.
举一反三:
【变式1】
8.若,求的平方根.
【变式2】
9.已知,求的平方根.
类型四、平方根 算术平方根估算 算术平方根的整数部分与小数部分
4.
10.如图,每个小正方形的边长均为,阴影部分是一个正方形.
(1)阴影部分的面积是__________,边长是____________;
(2)写出不大于阴影正方形边长的所有正整数;
(3)为阴影正方形边长的小数部分,为的整数部分,求的值.
举一反三:
【变式1】
11.已知=3,3a﹣b+1的平方根是±4,c是的整数部分,求a+b+2c的平方根.
【变式2】
12.设2+的整数部分和小数部分分别是x、y,试求x、y的值与x-1的算术平方根.
类型五、平方根 求代数式平方根
5.
13.已知是方程组的解,求的平方根.
举一反三:
【变式1】
14.已知的平方根是,的算术平方根是4.
(1)求a、b的值;
(2)求的平方根.
【变式2】
15.已知x﹣2和y﹣2互为相反数,求x+y的平方根.
类型六、平方根 利用平方根解方程
6.
16.求下列各式中的x.
(1),
(2).
举一反三:
【变式1】
17.解方程:
(1);
(2).
【变式2】
18.求下列各式中的的值.
(1)
(2)
类型七、平方根 算术平方根 规律题
7.
19.求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如,但可以通过计算器求.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n 16 0.16 0.0016 1600 160000 …
4 x 0.04 y 400 …
(1)表格中x= ;y= ;
(2)从表格中探究n与数位的规律,并利用这个规律解决下面两个问题:
①已知≈1.435,则≈ ;
②已知=1.83,若=0.183,则x= .
举一反三:
【变式1】
20.你能找出规律吗?
(1)计算: , , , ;
(2)根据找到的规律计算:;
(3)若,,用含a,b的式子表示.
【变式2】
21.(1)先完成下列表格:
a …… 0.0001 0.01 1 100 10000 ……
…… 0.01 ______ 1 ______ ______ ……
(2)由上表你发现什么规律?
(3)根据你发现的规律填空:
①已知=1.732则=______=______
②已知=0.056,则=______
类型八、平方根 应用 算术平方根 平方根
8.
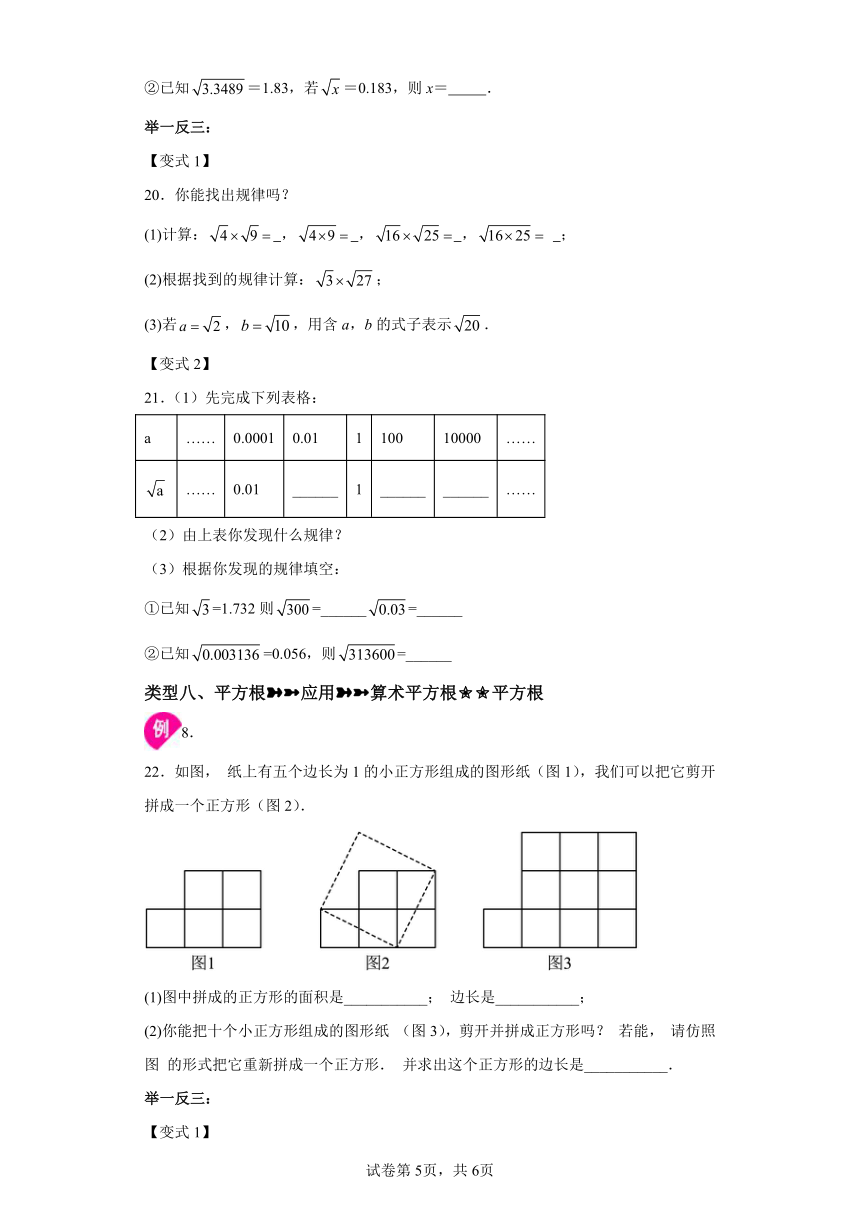
22.如图, 纸上有五个边长为1的小正方形组成的图形纸(图1),我们可以把它剪开拼成一个正方形(图2).
(1)图中拼成的正方形的面积是___________; 边长是___________;
(2)你能把十个小正方形组成的图形纸 (图3),剪开并拼成正方形吗? 若能, 请仿照图 的形式把它重新拼成一个正方形. 并求出这个正方形的边长是___________.
举一反三:
【变式1】
23.如图,用两个边长为cm的小正方形拼成一个大的正方形.
(1)求大正方形的边长:
(2)若沿此大正方形边长的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为48?
【变式2】
24.如图,有一块正方形铁皮,从四个顶点处分别剪掉一个面积为的正方形后,所剩部分正好围成一个无盖的长方体容器,量得该容器的体积是,求原正方形铁皮的边长.
中考真题专练
(2021·四川凉山·中考真题)
25.的平方根是( )
A. B. C. D.
(2013·山东淄博·中考真题)
26.实数9的算术平方根为( )
A.3 B. C. D.
(2020·甘肃金昌·中考真题)
27.若一个正方形的面积是12,则它的边长是( )
A. B.3 C. D.4
(2020·湖北荆州·中考真题)
28.若单项式与是同类项,则的值是 .
(2017·上海·中考真题)
29.方程=1的解是 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】平方根的定义:如果一个数的平方等于,这个数就叫做的平方根,也叫做的二次方根;算术平方根的概念:一般地,如果一个正数的平方等于,即,那么这个正数叫做的算术平方根;依此即可求解.
【详解】解:①负数没有平方根,故错误;
②正数和才有平方根,且正数有两个平方根,它们互为相反数,的平方根是,故错误;
③的算术平方根是,的算术平方根是,故正确;
④的平方根是,故正确;
故选:D.
【点睛】本题考查了平方根,熟练掌握平方根的定义是解本题的关键.
2.C
【分析】根据平方根和算术平方根的概念即可得到答案.
【详解】解:A、负数没有平方根,不符合题意,选项错误;
B、负数没有算术平方根,不符合题意,选项错误;
C、0的平方根与算术平方根都是0,符合题意,选项正确;
D、,的平方根,不符合题意,选项错误,
故选C.
【点睛】本题考查了平方根和算术平方根,解题关键是熟练掌握其定义,注意负数没有平方根和算术平方根,0的平方根与算术平方根都是0.
3.A
【分析】根据负数没有平方根,一个正数的平方根有两个,且两个平方根互为相反数,再逐一判断即可.
【详解】解:负数没有平方根,故(1)不符合题意;(2)不符合题意;(3)不符合题意;(4)符合题意;
故(5)不符合题意;
故选A.
【点睛】本题考查的是平方根的含义,掌握“一个正数有两个平方根,0的平方根是0,负数没有平方根”是解本题的关键.
4.
【分析】先求出,再求出16的平方根即可.
【详解】解:∵是的算术平方根,
∴.
∴16的平方根是.
故答案为:
【点睛】本题考查算术平方根以及平方根,解题的关键是理解算术平方根以及平方根的相关概念并会求一个数的算术平方根以及平方根.
5.
【分析】根据求一个数的算术平方根与平方根进行计算即可求解.
【详解】0.16的算术平方根是,,则的平方根是
故答案为:,
【点睛】本题考查了求一个数的算术平方根与平方根,理解平方根与算术平方根的定义是解题的关键.平方根:如果一个数的平方等于,那么这个数就叫的平方根,其中属于非负数的平方根称之为算术平方根.立方根:如果一个数的立方等于,那么这个数叫做的立方根.
6.a+2的平方根是
【分析】利用平方根及算术平方根列出式子,得到a的值,确定出a+2的值,即可求出平方根.
【详解】解:由题意得2a-1=9,3a+b-1=16,
解得:a=5,b=2,
则a+2=7,
∴a+2的平方根是.
【点睛】此题考查了平方根,以及算术平方根,读懂题意并列出式子是解本题的关键.
7.±3
【分析】根据算术平方根的非负性列出不等式,解不等式求出a,进而求出b,根据平方根的概念计算即可.
【详解】解:由题意得:a﹣17≥0,17﹣a≥0,
解得:a=17,
则b=﹣8,
∴a+b=9,
∵9的平方根是±3,
∴a+b的平方根是±3.
【点睛】本题考查的是算术平方根的非负性、平方根的概念,掌握被开方数是非负数是解题的关键.
8.
【分析】根据算术平方根的非负性,绝对值的非负性及偶次方的非负性得到,求出a,b,c的值,再根据平方根定义得到答案即可.
【详解】解:∵,
∴,
∴,
∴,
∴的平方根是.
【点睛】此题考查了算术平方根的非负性,绝对值的非负性及偶次方的非负性,求一个数的平方根,正确掌握各非负性是解题的关键.
9.±
【分析】首先根据非负数的性质列方程组求得a和b的值,然后求解.
【详解】解:∵,
∴a﹣3=0,b﹣4=0,
解得a=3,b=4,
∴,
∴.
【点睛】本题考查了非负数的性质,几个非负数的和等于0,则每个数是0,初中范围内的非负数有:数的偶次方、绝对值以及算术平方根.
10.(1)13,;(2)不大于的所有正整数为:1,2,3;(3)
【分析】(1)由大正方形的面积减去四个小三角形的面积即可得到阴影部分面积,根据算术平方根的定义即可求出边长;
(2)对进行估值,即可解答;
(3)对,估值,分别求出a,b的值即可.
【详解】解:(1)阴影部分面积为:,
∵阴影部分是一个正方形,
∴边长为:,
故答案为:13,.
(2)不大于的所有正整数为:1,2,3.
(3)∵,
∴,
∵
∴
∴.
【点睛】本题考查了无理数的估值及运算,解题的关键是掌握无理数的估值方法.
11.±5
【分析】分别根据算术平方根、平方根的意义,无理数的估算求出a、b、c的值,即可求出a+b+2c的值,根据平方根的意义即可求解.
【详解】解:∵=3,
∴2a﹣1=9,
解得:a=5,
∵3a﹣b+1的平方根是±4,
∴15﹣b+1=16,
解得:b=0,
∵,
∴10<<11,
∴c=10,
∴a+b+2c=5+0+2×10=25,
∴a+b+2c的平方根为=±5.
【点睛】本题考查了算术平方根、平方根的意义,无理数的估算,熟知算术平方根、平方根的意义是解题关键.
12..
【详解】试题分析:先找到介于哪两个整数之间,从而找到整数部分,小数部分让原数减去整数部分,然后代入求值即可.
试题解析:因为4<6<9,所以2<<3,
即的整数部分是2,
所以2+的整数部分是4,小数部分是2+-4=-2,
即x=4,y=-2,所以=.
考点:1.估算无理数的大小;2.算术平方根.
13.±1
【分析】将a与b代入值代入方程组计算求出m与n的值即可.
【详解】解:将
代入方程组
可得:
解得:,
所以(m+n)2018=1,
所以(m+n)2018的平方根是±1.
【点睛】此题考查了解二元一次方程组和平方根的定义,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
14.(1)a=5,b=4;
(2).
【分析】(1)根据平方根,算术平方根的定义,求解即可;
(2)根据平方根定义,求解即可.
【详解】(1)解:∵的平方根是,的算术平方根是4.
∴,,解得a=5,b=4.
(2)解:当a=5,b=4时,ab+5=25 ,而25的平方根为,
即ab+5的平方根是.
【点睛】此题主要考查平方根和算术平方根,解题的关键是熟知平方根,算术平方根的定义.
15.±2
【分析】根据相反数的定义可求x+y,再根据平方根的定义可得答案.
【详解】解:∵x﹣2和y﹣2互为相反数,
∴x﹣2+y﹣2=0,
∴x+y=4,4的平方根是±2.
故x+y的平方根是±2.
【点睛】本题考查了相反数的性质和平方根的定义,属于基本题型,熟练掌握以上基本知识是解题关键.
16.(1)
(2)
【分析】(1)先移项,然后利用平方根求解方程即可;
(2)先移项,然后利用平方根求解方程即可.
【详解】(1)解:
移项得:,
∴,
∴,
∴
(2)
,
∴
∴
∴.
【点睛】题目主要考查利用平方根解方程,熟练掌握解方程方法是解题关键.
17.(1)或
(2)或
【分析】(1)先将方程整理为,再利用平方根解方程即可得;
(2)先将方程整理为,再利用平方根解方程即可得.
【详解】(1)解:,
,
,
或.
(2)解:,
,
,
或,
或.
【点睛】本题考查了利用平方根解方程,熟练掌握平方根的性质是解题关键.
18.(1)
(2)或
【分析】根据平方根的定义求解.
【详解】(1)解:
(2)解:
或
【点睛】本题考查了利用平方根解方程,解题的关键是理解平方根的概念.
19.(1)0.4;40
(2)①143.5;②0.03489
【分析】(1)把n=0.16代入x=求解即可;把n=1600代入y=求解即可;
(2)①根据被开方数小数点向右移动了4位,则算术平方根小数点向右移动两位求解;
②根据算术平方根小数点向左移动1位;则被开方数小数点向左移动了2位求解.
【详解】(1)解:当n=0.16时,x===0.4,
当n=1006时,x===40,
故答案为:0.4,40;
(2)解:①已知≈1.435,则≈143.5;
故答案为:143.5;
②已知=1.83,若=0.183,则x=0.03489.
故答案为:0.03489.
【点睛】本题考查了算术平方根,解题的关键在于从小数点的移动位数考虑.
20.(1)6;6;20;20;规律见解析;
(2)9
(3)
【分析】(1)首先求出每个算式的值是多少,然后总结出规律:(a≥0,b≥0),据此判断即可.
(2)根据进行解答即可.
(3)根据,,可得,据此解答即可.
【详解】(1)∵,,,,
∴总结出的规律是:(a≥0,b≥0).
故答案为:6;6;20;20
(2);
(3)∵,,
∴,
【点睛】此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是注意观察总结出规律,并能正确的应用规律.
21.(1)0.1,10,100;(2)被开方数的小数点向左或向右每移动两位开方后所得的结果相应的也向左或向右移动1位;(3)17.32,0.1732,560
【分析】(1)直接利用已知数据开平方得出答案;
(2)利用原数据与开平方后的数据变化得出一般性规律是被开方数的小数点向左或向右每移动两位开方后所得的结果相应的也向左或向右移动1位;
(3)利用(2)中发现的规律进而分别得出各数据答案.
【详解】解:(1)
a …… 0.0001 0.01 1 100 10000 ……
…… 0.01 0.1 1 10 100 ……
(2)规律是:被开方数的小数点向左或向右每移动两位开方后所得的结果相应的也向左或向右移动1位;
(3)①∵=1.732,∴=17.32;
=0.1732;
②∵=0.056,∴=560.
故答案为①17.32;0.1732;②560.
【点睛】此题主要考查了算术平方根,正确发现数据开平方后的变化规律是解题关键.
22.(1) ;
(2)剪拼图见解析;
【分析】(1)拼成的正方形面积等于原五个小正方形的面积;进一步求边长即可;
(2)仿照(1)中的方法剪拼,根据大正方形的面积求边长即可;
【详解】(1)解:∵拼成的正方形面积等于原五个小正方形的面积
∴拼成的正方形面积为:
由正方形的面积公式可得:
(2)解:剪拼图如下:
∵拼成的正方形面积等于原10个小正方形的面积
∴拼成的正方形面积为:
由正方形的面积公式可得:
【点睛】本题考查了算术平方根;熟练掌握图形的拆补是解题的关键.
23.(1)大正方形的边长为8cm
(2)沿此大正方形边的方向剪出一个长方形,能使剪出的长方形纸片的长宽之比为4:3,且面积为48
【分析】(1)根据已知正方形的面积关系即可求出大正方形的边长;
(2)先求出长方形的边长,再判断即可.
【详解】(1)解:大正方形的边长为acm,则,
∵,
∴.
答:大正方形的边长为8cm.
(2)解:设长方形纸片的长为4xcm,宽为3xcm,则,
解得,
∵,
∴,
,,
∵大正方形的边长为8cm,符合.
所以沿此大正方形边的方向剪出一个长方形,能使剪出的长方形纸片的长宽之比为4:3,且面积为48.
【点睛】本题考查了平方根的实际应用,能根据题意列出算式是解此题的关键.
24.
【分析】设原来正方形的边长为,然后根据长方体容积公式列方程计算.
【详解】解:从四个顶点处分别剪掉一个面积为25的正方形,
剪掉的正方形边长为5,
设原来正方形的边长为,
由题意可得:,
,
,
解得:或(不合题意,舍去),
原来正方形的边长为16.
【点睛】本题考查平方根的实际应用,理解平方根的概念并掌握求一个长方体容积的方法准确列方程求解是解题关键.
25.A
【分析】根据平方根的定义求解即可.
【详解】解:,
的平方根是,
故选:.
【点睛】本题考查了平方根的定义,熟练掌握平方根的定义是解答本题的关键,如果一个数的平方等于a,则这个数叫做a的平方根,即x2=a,那么x叫做a的平方根,记作.
26.A
【分析】根据算术平方根的定义,即可求出结果.
【详解】解:∵,
∴.
故选:A
【点睛】本题考查了算术平方根,解本题的关键在熟练掌握算术平方根的定义.算术平方根的定义:一般地,如果一个正数的平方等于,即,那么这个正数就叫做的算术平方根.
27.A
【分析】根据正方形的面积公式即可求解.
【详解】解:由题意知:正方形的面积等于边长×边长,设边长为a,
故a =12,
∴a=±,又边长大于0
∴边长a=.
故选:A.
【点睛】本题考查了正方形的面积公式,开平方运算等,属于基础题.
28.2
【分析】先根据同类项的定义求出m与n的值,再代入计算算术平方根即可得.
【详解】由同类项的定义得:
解得
则
故答案为:2.
【点睛】本题考查了同类项的定义、算术平方根,熟记同类项的定义是解题关键.
29.x=2
【详解】=1,两边平方得,2x﹣3=1,
解得,x=2;
经检验,x=2是方程的根;
故答案为x=2.
考点:解无理方程.
答案第1页,共2页
答案第1页,共2页
【学习目标】
1.了解平方根、算术平方根的概念,会用根号表示数的平方根.
2.了解开方与乘方互为逆运算,会用开方运算求某些非负数的平方根,会用计算器求平方根.
【要点梳理】
知识点一、平方根和算术平方根的概念
1.算术平方根的定义
如果一个正数的平方等于,即,那么这个正数叫做的算术平方根(规定0的算术平方根还是0);的算术平方根记作,读作“的算术平方根”,叫做被开方数.
特别说明:当式子有意义时,一定表示一个非负数,即≥0,≥0.
2.平方根的定义
如果,那么叫做的平方根.求一个数的平方根的运算,叫做开平方.平方与开平方互为逆运算. (≥0)的平方根的符号表达为,其中是的算术平方根.
知识点二、平方根和算术平方根的区别与联系
1.区别:(1)定义不同;(2)结果不同:和
2.联系:(1)平方根包含算术平方根;
(2)被开方数都是非负数;
(3)0的平方根和算术平方根均为0.
特别说明:(1)正数的平方根有两个,它们互为相反数,其中正的那个叫它的算术平方根;负数没有平方根.
(2)正数的两个平方根互为相反数,根据它的算术平方根可以立即写出它的另一个平方根.因此,我们可以利用算术平方根来研究平方根.
知识点三、平方根的性质
知识点四、平方根小数点位数移动规律
被开方数的小数点向右或者向左移动2位,它的算术平方根的小数点就相应地向右或者向左移动1位.例如:,,,.
【典型例题】
类型一、平方根 概念的理解 平方根 算术平方根
1.
1.下列说法:①的平方根是±0.5;②任何数的平方都是非负数,因而任何数的平方根也是非负数;③算术平方根等于它本身的数是0,1;④平方根等于本身的数是0,其中正确的是( )
A.④ B.①② C.②③④ D.③④
举一反三:
【变式1】
2.下列说法中正确的是( )
A.的平方根为 B.的算术平方根为
C.0的平方根与算术平方根都是0 D.的平方根为
【变式2】
3.下列说法:(1)任何一个数都有两个平方根,它们互为相反数;(2)数a的平方根是±;(3)的算术平方根是2;(4)负数不能开平方; (5),其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
类型二、平方根 求一个数的平方根与算术平方根
2.
4.若是的算术平方根,则的平方根是 .
举一反三:
【变式1】
5.0.16的算术平方根是 ,的平方根是 .
【变式2】
6.已知2a-1的算术平方根为3,3a+b-1的算术平方根为4,求a+2的平方根.
类型三、平方根 平方根 算术平方根的非负性
3.
7.已知=b+8,求a+b的平方根.
举一反三:
【变式1】
8.若,求的平方根.
【变式2】
9.已知,求的平方根.
类型四、平方根 算术平方根估算 算术平方根的整数部分与小数部分
4.
10.如图,每个小正方形的边长均为,阴影部分是一个正方形.
(1)阴影部分的面积是__________,边长是____________;
(2)写出不大于阴影正方形边长的所有正整数;
(3)为阴影正方形边长的小数部分,为的整数部分,求的值.
举一反三:
【变式1】
11.已知=3,3a﹣b+1的平方根是±4,c是的整数部分,求a+b+2c的平方根.
【变式2】
12.设2+的整数部分和小数部分分别是x、y,试求x、y的值与x-1的算术平方根.
类型五、平方根 求代数式平方根
5.
13.已知是方程组的解,求的平方根.
举一反三:
【变式1】
14.已知的平方根是,的算术平方根是4.
(1)求a、b的值;
(2)求的平方根.
【变式2】
15.已知x﹣2和y﹣2互为相反数,求x+y的平方根.
类型六、平方根 利用平方根解方程
6.
16.求下列各式中的x.
(1),
(2).
举一反三:
【变式1】
17.解方程:
(1);
(2).
【变式2】
18.求下列各式中的的值.
(1)
(2)
类型七、平方根 算术平方根 规律题
7.
19.求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如,但可以通过计算器求.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n 16 0.16 0.0016 1600 160000 …
4 x 0.04 y 400 …
(1)表格中x= ;y= ;
(2)从表格中探究n与数位的规律,并利用这个规律解决下面两个问题:
①已知≈1.435,则≈ ;
②已知=1.83,若=0.183,则x= .
举一反三:
【变式1】
20.你能找出规律吗?
(1)计算: , , , ;
(2)根据找到的规律计算:;
(3)若,,用含a,b的式子表示.
【变式2】
21.(1)先完成下列表格:
a …… 0.0001 0.01 1 100 10000 ……
…… 0.01 ______ 1 ______ ______ ……
(2)由上表你发现什么规律?
(3)根据你发现的规律填空:
①已知=1.732则=______=______
②已知=0.056,则=______
类型八、平方根 应用 算术平方根 平方根
8.
22.如图, 纸上有五个边长为1的小正方形组成的图形纸(图1),我们可以把它剪开拼成一个正方形(图2).
(1)图中拼成的正方形的面积是___________; 边长是___________;
(2)你能把十个小正方形组成的图形纸 (图3),剪开并拼成正方形吗? 若能, 请仿照图 的形式把它重新拼成一个正方形. 并求出这个正方形的边长是___________.
举一反三:
【变式1】
23.如图,用两个边长为cm的小正方形拼成一个大的正方形.
(1)求大正方形的边长:
(2)若沿此大正方形边长的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为48?
【变式2】
24.如图,有一块正方形铁皮,从四个顶点处分别剪掉一个面积为的正方形后,所剩部分正好围成一个无盖的长方体容器,量得该容器的体积是,求原正方形铁皮的边长.
中考真题专练
(2021·四川凉山·中考真题)
25.的平方根是( )
A. B. C. D.
(2013·山东淄博·中考真题)
26.实数9的算术平方根为( )
A.3 B. C. D.
(2020·甘肃金昌·中考真题)
27.若一个正方形的面积是12,则它的边长是( )
A. B.3 C. D.4
(2020·湖北荆州·中考真题)
28.若单项式与是同类项,则的值是 .
(2017·上海·中考真题)
29.方程=1的解是 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】平方根的定义:如果一个数的平方等于,这个数就叫做的平方根,也叫做的二次方根;算术平方根的概念:一般地,如果一个正数的平方等于,即,那么这个正数叫做的算术平方根;依此即可求解.
【详解】解:①负数没有平方根,故错误;
②正数和才有平方根,且正数有两个平方根,它们互为相反数,的平方根是,故错误;
③的算术平方根是,的算术平方根是,故正确;
④的平方根是,故正确;
故选:D.
【点睛】本题考查了平方根,熟练掌握平方根的定义是解本题的关键.
2.C
【分析】根据平方根和算术平方根的概念即可得到答案.
【详解】解:A、负数没有平方根,不符合题意,选项错误;
B、负数没有算术平方根,不符合题意,选项错误;
C、0的平方根与算术平方根都是0,符合题意,选项正确;
D、,的平方根,不符合题意,选项错误,
故选C.
【点睛】本题考查了平方根和算术平方根,解题关键是熟练掌握其定义,注意负数没有平方根和算术平方根,0的平方根与算术平方根都是0.
3.A
【分析】根据负数没有平方根,一个正数的平方根有两个,且两个平方根互为相反数,再逐一判断即可.
【详解】解:负数没有平方根,故(1)不符合题意;(2)不符合题意;(3)不符合题意;(4)符合题意;
故(5)不符合题意;
故选A.
【点睛】本题考查的是平方根的含义,掌握“一个正数有两个平方根,0的平方根是0,负数没有平方根”是解本题的关键.
4.
【分析】先求出,再求出16的平方根即可.
【详解】解:∵是的算术平方根,
∴.
∴16的平方根是.
故答案为:
【点睛】本题考查算术平方根以及平方根,解题的关键是理解算术平方根以及平方根的相关概念并会求一个数的算术平方根以及平方根.
5.
【分析】根据求一个数的算术平方根与平方根进行计算即可求解.
【详解】0.16的算术平方根是,,则的平方根是
故答案为:,
【点睛】本题考查了求一个数的算术平方根与平方根,理解平方根与算术平方根的定义是解题的关键.平方根:如果一个数的平方等于,那么这个数就叫的平方根,其中属于非负数的平方根称之为算术平方根.立方根:如果一个数的立方等于,那么这个数叫做的立方根.
6.a+2的平方根是
【分析】利用平方根及算术平方根列出式子,得到a的值,确定出a+2的值,即可求出平方根.
【详解】解:由题意得2a-1=9,3a+b-1=16,
解得:a=5,b=2,
则a+2=7,
∴a+2的平方根是.
【点睛】此题考查了平方根,以及算术平方根,读懂题意并列出式子是解本题的关键.
7.±3
【分析】根据算术平方根的非负性列出不等式,解不等式求出a,进而求出b,根据平方根的概念计算即可.
【详解】解:由题意得:a﹣17≥0,17﹣a≥0,
解得:a=17,
则b=﹣8,
∴a+b=9,
∵9的平方根是±3,
∴a+b的平方根是±3.
【点睛】本题考查的是算术平方根的非负性、平方根的概念,掌握被开方数是非负数是解题的关键.
8.
【分析】根据算术平方根的非负性,绝对值的非负性及偶次方的非负性得到,求出a,b,c的值,再根据平方根定义得到答案即可.
【详解】解:∵,
∴,
∴,
∴,
∴的平方根是.
【点睛】此题考查了算术平方根的非负性,绝对值的非负性及偶次方的非负性,求一个数的平方根,正确掌握各非负性是解题的关键.
9.±
【分析】首先根据非负数的性质列方程组求得a和b的值,然后求解.
【详解】解:∵,
∴a﹣3=0,b﹣4=0,
解得a=3,b=4,
∴,
∴.
【点睛】本题考查了非负数的性质,几个非负数的和等于0,则每个数是0,初中范围内的非负数有:数的偶次方、绝对值以及算术平方根.
10.(1)13,;(2)不大于的所有正整数为:1,2,3;(3)
【分析】(1)由大正方形的面积减去四个小三角形的面积即可得到阴影部分面积,根据算术平方根的定义即可求出边长;
(2)对进行估值,即可解答;
(3)对,估值,分别求出a,b的值即可.
【详解】解:(1)阴影部分面积为:,
∵阴影部分是一个正方形,
∴边长为:,
故答案为:13,.
(2)不大于的所有正整数为:1,2,3.
(3)∵,
∴,
∵
∴
∴.
【点睛】本题考查了无理数的估值及运算,解题的关键是掌握无理数的估值方法.
11.±5
【分析】分别根据算术平方根、平方根的意义,无理数的估算求出a、b、c的值,即可求出a+b+2c的值,根据平方根的意义即可求解.
【详解】解:∵=3,
∴2a﹣1=9,
解得:a=5,
∵3a﹣b+1的平方根是±4,
∴15﹣b+1=16,
解得:b=0,
∵,
∴10<<11,
∴c=10,
∴a+b+2c=5+0+2×10=25,
∴a+b+2c的平方根为=±5.
【点睛】本题考查了算术平方根、平方根的意义,无理数的估算,熟知算术平方根、平方根的意义是解题关键.
12..
【详解】试题分析:先找到介于哪两个整数之间,从而找到整数部分,小数部分让原数减去整数部分,然后代入求值即可.
试题解析:因为4<6<9,所以2<<3,
即的整数部分是2,
所以2+的整数部分是4,小数部分是2+-4=-2,
即x=4,y=-2,所以=.
考点:1.估算无理数的大小;2.算术平方根.
13.±1
【分析】将a与b代入值代入方程组计算求出m与n的值即可.
【详解】解:将
代入方程组
可得:
解得:,
所以(m+n)2018=1,
所以(m+n)2018的平方根是±1.
【点睛】此题考查了解二元一次方程组和平方根的定义,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
14.(1)a=5,b=4;
(2).
【分析】(1)根据平方根,算术平方根的定义,求解即可;
(2)根据平方根定义,求解即可.
【详解】(1)解:∵的平方根是,的算术平方根是4.
∴,,解得a=5,b=4.
(2)解:当a=5,b=4时,ab+5=25 ,而25的平方根为,
即ab+5的平方根是.
【点睛】此题主要考查平方根和算术平方根,解题的关键是熟知平方根,算术平方根的定义.
15.±2
【分析】根据相反数的定义可求x+y,再根据平方根的定义可得答案.
【详解】解:∵x﹣2和y﹣2互为相反数,
∴x﹣2+y﹣2=0,
∴x+y=4,4的平方根是±2.
故x+y的平方根是±2.
【点睛】本题考查了相反数的性质和平方根的定义,属于基本题型,熟练掌握以上基本知识是解题关键.
16.(1)
(2)
【分析】(1)先移项,然后利用平方根求解方程即可;
(2)先移项,然后利用平方根求解方程即可.
【详解】(1)解:
移项得:,
∴,
∴,
∴
(2)
,
∴
∴
∴.
【点睛】题目主要考查利用平方根解方程,熟练掌握解方程方法是解题关键.
17.(1)或
(2)或
【分析】(1)先将方程整理为,再利用平方根解方程即可得;
(2)先将方程整理为,再利用平方根解方程即可得.
【详解】(1)解:,
,
,
或.
(2)解:,
,
,
或,
或.
【点睛】本题考查了利用平方根解方程,熟练掌握平方根的性质是解题关键.
18.(1)
(2)或
【分析】根据平方根的定义求解.
【详解】(1)解:
(2)解:
或
【点睛】本题考查了利用平方根解方程,解题的关键是理解平方根的概念.
19.(1)0.4;40
(2)①143.5;②0.03489
【分析】(1)把n=0.16代入x=求解即可;把n=1600代入y=求解即可;
(2)①根据被开方数小数点向右移动了4位,则算术平方根小数点向右移动两位求解;
②根据算术平方根小数点向左移动1位;则被开方数小数点向左移动了2位求解.
【详解】(1)解:当n=0.16时,x===0.4,
当n=1006时,x===40,
故答案为:0.4,40;
(2)解:①已知≈1.435,则≈143.5;
故答案为:143.5;
②已知=1.83,若=0.183,则x=0.03489.
故答案为:0.03489.
【点睛】本题考查了算术平方根,解题的关键在于从小数点的移动位数考虑.
20.(1)6;6;20;20;规律见解析;
(2)9
(3)
【分析】(1)首先求出每个算式的值是多少,然后总结出规律:(a≥0,b≥0),据此判断即可.
(2)根据进行解答即可.
(3)根据,,可得,据此解答即可.
【详解】(1)∵,,,,
∴总结出的规律是:(a≥0,b≥0).
故答案为:6;6;20;20
(2);
(3)∵,,
∴,
【点睛】此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是注意观察总结出规律,并能正确的应用规律.
21.(1)0.1,10,100;(2)被开方数的小数点向左或向右每移动两位开方后所得的结果相应的也向左或向右移动1位;(3)17.32,0.1732,560
【分析】(1)直接利用已知数据开平方得出答案;
(2)利用原数据与开平方后的数据变化得出一般性规律是被开方数的小数点向左或向右每移动两位开方后所得的结果相应的也向左或向右移动1位;
(3)利用(2)中发现的规律进而分别得出各数据答案.
【详解】解:(1)
a …… 0.0001 0.01 1 100 10000 ……
…… 0.01 0.1 1 10 100 ……
(2)规律是:被开方数的小数点向左或向右每移动两位开方后所得的结果相应的也向左或向右移动1位;
(3)①∵=1.732,∴=17.32;
=0.1732;
②∵=0.056,∴=560.
故答案为①17.32;0.1732;②560.
【点睛】此题主要考查了算术平方根,正确发现数据开平方后的变化规律是解题关键.
22.(1) ;
(2)剪拼图见解析;
【分析】(1)拼成的正方形面积等于原五个小正方形的面积;进一步求边长即可;
(2)仿照(1)中的方法剪拼,根据大正方形的面积求边长即可;
【详解】(1)解:∵拼成的正方形面积等于原五个小正方形的面积
∴拼成的正方形面积为:
由正方形的面积公式可得:
(2)解:剪拼图如下:
∵拼成的正方形面积等于原10个小正方形的面积
∴拼成的正方形面积为:
由正方形的面积公式可得:
【点睛】本题考查了算术平方根;熟练掌握图形的拆补是解题的关键.
23.(1)大正方形的边长为8cm
(2)沿此大正方形边的方向剪出一个长方形,能使剪出的长方形纸片的长宽之比为4:3,且面积为48
【分析】(1)根据已知正方形的面积关系即可求出大正方形的边长;
(2)先求出长方形的边长,再判断即可.
【详解】(1)解:大正方形的边长为acm,则,
∵,
∴.
答:大正方形的边长为8cm.
(2)解:设长方形纸片的长为4xcm,宽为3xcm,则,
解得,
∵,
∴,
,,
∵大正方形的边长为8cm,符合.
所以沿此大正方形边的方向剪出一个长方形,能使剪出的长方形纸片的长宽之比为4:3,且面积为48.
【点睛】本题考查了平方根的实际应用,能根据题意列出算式是解此题的关键.
24.
【分析】设原来正方形的边长为,然后根据长方体容积公式列方程计算.
【详解】解:从四个顶点处分别剪掉一个面积为25的正方形,
剪掉的正方形边长为5,
设原来正方形的边长为,
由题意可得:,
,
,
解得:或(不合题意,舍去),
原来正方形的边长为16.
【点睛】本题考查平方根的实际应用,理解平方根的概念并掌握求一个长方体容积的方法准确列方程求解是解题关键.
25.A
【分析】根据平方根的定义求解即可.
【详解】解:,
的平方根是,
故选:.
【点睛】本题考查了平方根的定义,熟练掌握平方根的定义是解答本题的关键,如果一个数的平方等于a,则这个数叫做a的平方根,即x2=a,那么x叫做a的平方根,记作.
26.A
【分析】根据算术平方根的定义,即可求出结果.
【详解】解:∵,
∴.
故选:A
【点睛】本题考查了算术平方根,解本题的关键在熟练掌握算术平方根的定义.算术平方根的定义:一般地,如果一个正数的平方等于,即,那么这个正数就叫做的算术平方根.
27.A
【分析】根据正方形的面积公式即可求解.
【详解】解:由题意知:正方形的面积等于边长×边长,设边长为a,
故a =12,
∴a=±,又边长大于0
∴边长a=.
故选:A.
【点睛】本题考查了正方形的面积公式,开平方运算等,属于基础题.
28.2
【分析】先根据同类项的定义求出m与n的值,再代入计算算术平方根即可得.
【详解】由同类项的定义得:
解得
则
故答案为:2.
【点睛】本题考查了同类项的定义、算术平方根,熟记同类项的定义是解题关键.
29.x=2
【详解】=1,两边平方得,2x﹣3=1,
解得,x=2;
经检验,x=2是方程的根;
故答案为x=2.
考点:解无理方程.
答案第1页,共2页
答案第1页,共2页
