专题7.2平面直角坐标系 基础篇 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题7.2平面直角坐标系 基础篇 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 555.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 19:00:27 | ||
图片预览


文档简介
专题7.2 平面直角坐标系(基础篇)(专项练习)
一、单选题
1.下列表述中,能确定物体位置的是( )
A.万达影城1号厅2排 B.温泉南路
C.南偏西 D.东经,北纬
2.已知点P在第四象限,且到x轴的距离是2,到y轴的距离是7,则点P的坐标为( )
A. B. C. D.
3.点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )
A.(3, 3) B.(3,-3) C.(6,-6) D.(3,3)或
4.点A(m+3,m+1)在y轴上,则点A的坐标为( )
A.(0,-2) B.(2,0) C.(4,y) D.(0,-4)
5.如图,小手盖住的点的坐标可能为( )
A. B. C. D.
6.如图,已知正方形,顶点,,,规定“把正方形先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2019次变换后,正方形的对角线交点M的坐标变为( )
A. B. C. D.
7.在平面直角坐标系内,点P(,)在第四象限,则的取值范围是( )
A. B. C. D.
8.下列说法正确的是( )
A.若点,则点A到x轴的距离为3 B.平行于y轴的直线上所有点的纵坐标都相同
C.与表示两个不同的点 D.若点在x轴上,则
9.如图在平面直角坐标系中,点A、B、C的坐标分别为,,,则的面积是( )
A.5 B.10 C.75 D.15
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点,第次接着运动到点,第次接着运动到点,…,按这样的运动规律,经过第次运动后,动点的坐标是( )
A. B. C. D.
二、填空题
11.若四排三列用有序实数对来表示,那么表示一排五列的有序实数对为 .
12.已知,则在 象限.
13.点在第二象限,则x的取值范围是 .
14.已知轴,A点的坐标为,并且,则B的坐标为 .
15.已知点在象限角平分线上,则的值为 .
16.在平面直角坐标系中,点A(2a+4,6﹣2a)在第四象限,则a的取值范围是 .
17.如图所示,在平面直角坐标系中,点,,,则四边形ABCO的面积为 .
18.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点、的坐标分别为、,则顶点的坐标为 .
三、解答题
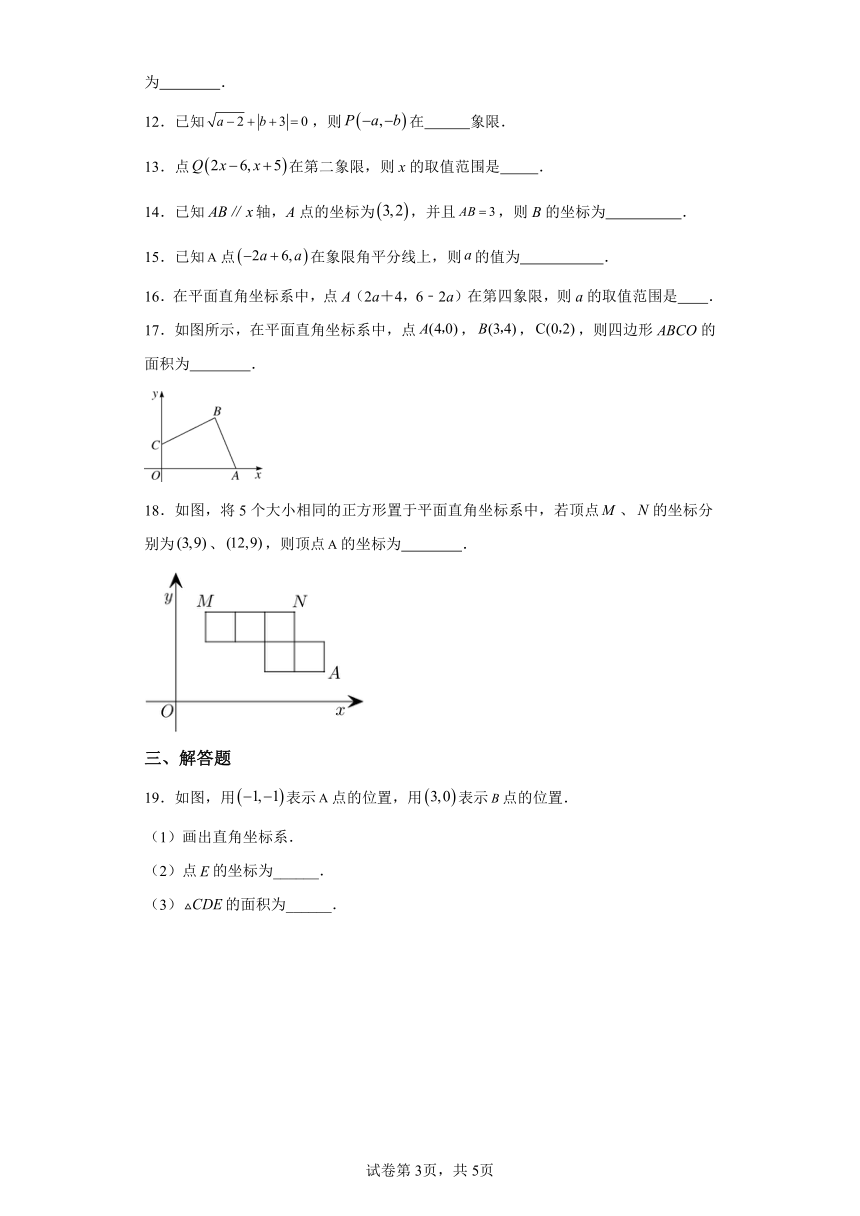
19.如图,用表示点的位置,用表示点的位置.
(1)画出直角坐标系.
(2)点的坐标为______.
(3)的面积为______.
20.在平面直角坐标系中,已知点.
(1)若点M在y轴上,求m的值;
(2)若点M到y轴的距离是3,求m的值;
(3)若点M在第一、三象限的角平分线上,求m的值.
21.已知平面直角坐标系中有一点P(2m+1,m﹣3).
(1)若点P在第四象限,求m的取值范围;
(2)若点P到y轴的距离为3,求点P的坐标.
22.已知平面直角坐标系内有4个点:A(0,2),B(-2,0),C(1,-1),D(3,1).
(1)在平面直角坐标系中描出这4个点;
(2)顺次连接A、B、C、D组成四边形ABCD,请用两种方法求出四边形ABCD的面积.
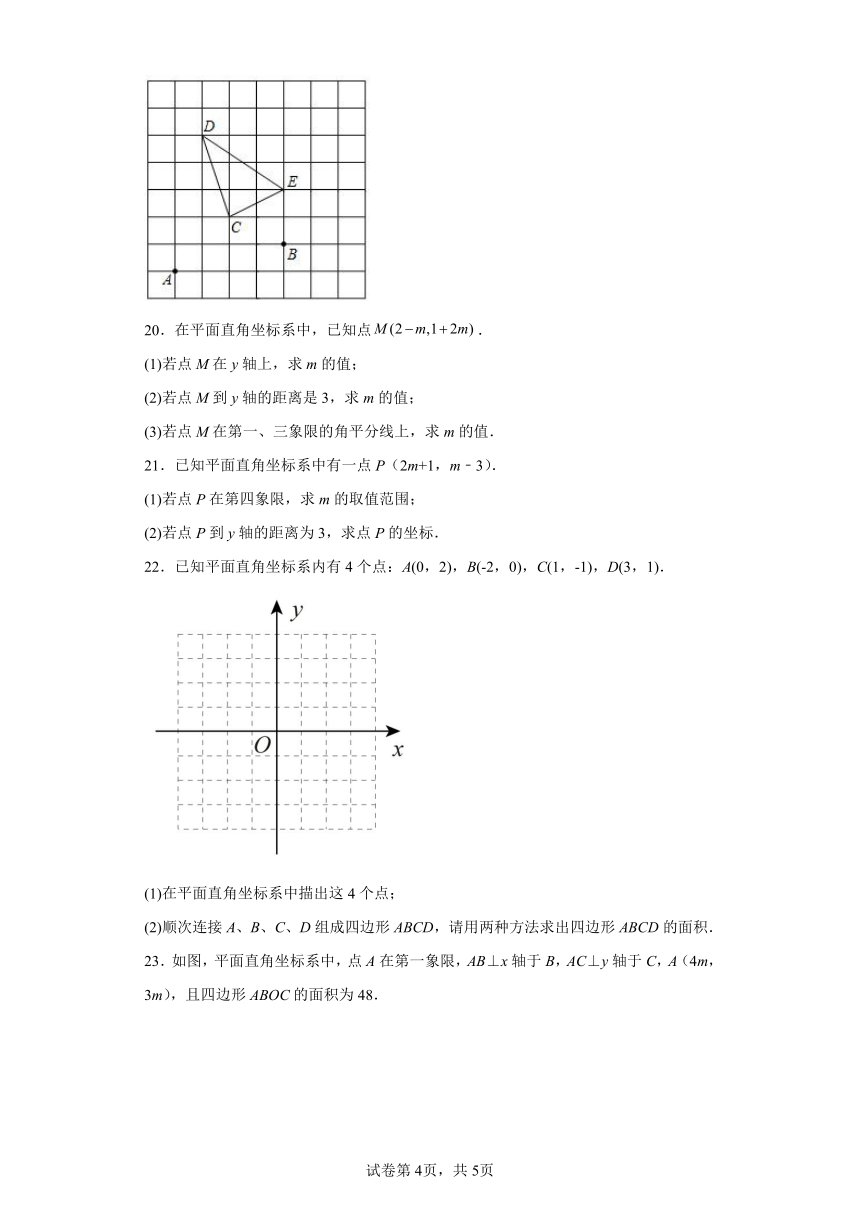
23.如图,平面直角坐标系中,点A在第一象限,AB⊥x轴于B,AC⊥y轴于C,A(4m,3m),且四边形ABOC的面积为48.
(1)如图①,求A点的坐标;
(2)如图②,点D从O出发以每秒1个单位的速度沿y轴正半轴运动,同时点E从A出发,以每秒2个单位的速度沿射线BA运动,DE交线段AC于F,设运动的时间为t,当S△AEF<S△CDF时,求t的取值范围.
24.平面直角坐标系是由原点重合且互相垂直的两条数轴构成的,它是沟通代数与几何的桥梁,是非常重要的数学工具.
(1)最早引入坐标系,用代数方法研究几何图形的数学家是( )
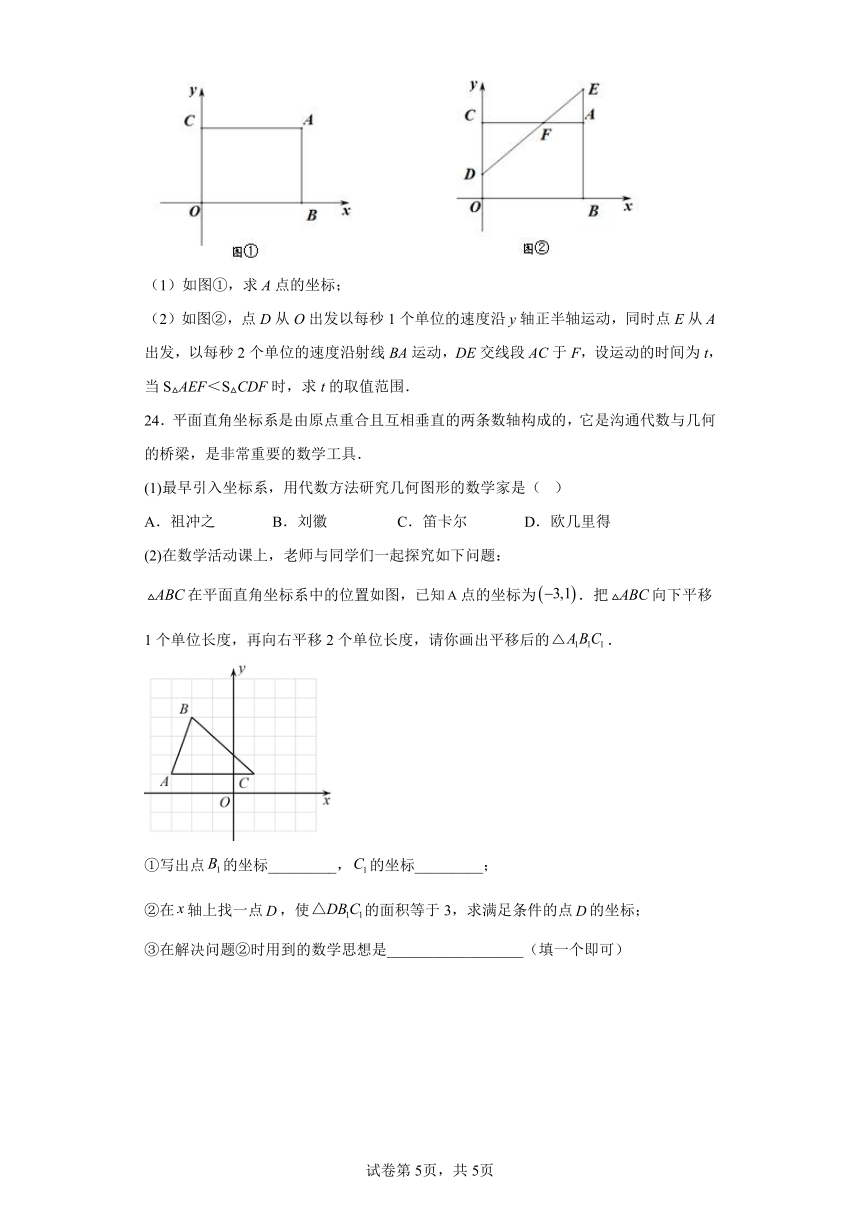
A.祖冲之 B.刘徽 C.笛卡尔 D.欧几里得
(2)在数学活动课上,老师与同学们一起探究如下问题:
在平面直角坐标系中的位置如图,已知点的坐标为.把向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的.
①写出点的坐标_________,的坐标_________;
②在轴上找一点,使的面积等于3,求满足条件的点的坐标;
③在解决问题②时用到的数学思想是__________________(填一个即可)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据确定位置的有序数对有两个数解答.
【详解】解:在平面直角坐标系中,要用两个数据才能表示一个点的位置,纵观各选项,只有东经,北纬能确定物体的位置,
故选:D
【点睛】本题考查了坐标确定位置,理解在平面直角坐标系中,要用两个数据才能表示一个点的位置是解题的关键.
2.A
【分析】根据第四象限坐标特征,及点P分别到x轴和y轴的距离可得答案.
【详解】解:点P在第四象限,到x轴的距离是2,到y轴的距离是7,
点P横坐标为7,纵坐标为-2,
点P的坐标,
故选:A.
【点睛】此题考查了四象限的点坐标特征,掌握第四象限中的点是解题关键.
3.D
【分析】由点P到两坐标轴的距离相等,建立绝对值方程再解方程即可得到答案.
【详解】解: 点P到两坐标轴的距离相等,
或
当时,
当
综上:的坐标为:或
故选D.
【点睛】本题考查的是平面直角坐标系内点的坐标特点,点到坐标轴的距离与坐标的关系,一元一次方程的解法,掌握以上知识是解题的关键.
4.A
【分析】根据点在y轴上,点的横坐标为0即可求解.
【详解】解:由题意知,点A(m+3,m+1)在y轴上,则该点的横坐标为0,
∴m+3=0,
∴m=-3,代入,此时点A(0,-2),
故选:A.
【点睛】本题考查了平面直角坐标系中点的特征,熟练掌握平面直角坐标系中坐标轴上点的坐标特征是解决本题的关键.
5.D
【分析】根据各象限内点的坐标特征解题,四个象限的符号特征为:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-) .
【详解】小手盖住的是第四象限的点,其点坐标特征为:横坐标为正数,纵坐标为负数,
故选:D.
【点睛】本题考查象限及点的坐标的有关性质等知识,是基础考点,难度较易,掌握相关知识是解题关键.
6.C
【分析】依次按要求变化后写出坐标,得出坐标与变化次数n的关系即可.
【详解】解:∵正方形,顶点,,,
∴正方形的对角线交点M的坐标为,
∵把正方形先沿x轴翻折,再向左平移1个单位长度为一次变换,
∴第一次变换后点M的坐标为,第二次变换后点M的坐标为,第三次变换后点M的坐标为,第四次变换后点M的坐标为
可以发现点n次后,当n为偶数,点M的坐标为,
当n是奇数,点M的坐标为,
∴连续经过2019次变换后,正方形的对角线交点M的坐标变为,
故选:C.
【点睛】本题主要考查坐标系上点翻折,平移后点的坐标,依据要求正确求出变化后点的坐标是解题关键.
7.C
【详解】解:点P(,)在第四象限,根据第四象限点的坐标特征,
则
解得:
故选C.
8.C
【分析】根据平面直角坐标系内点的坐标特点分别进行判断,即可得出结论.
【详解】解:A、若点,则点A到y轴的距离为3;故此选项说法错误,不符合题意;
B、平行于y轴的直线上所有点的横坐标都相同;故此选项说法错误,不符合题意;
C、与表示两个不同的点;故此选项说法正确,符合题意;
D、若点在x轴上,则;故此选项说法错误,不符合题意.
故选:C.
【点睛】本题考查了平面直角坐标系,解题的关键是熟练掌握平面直角坐标系内点的坐标特点是解题的关键.
9.A
【分析】过点A做垂直于x轴,垂足为D,则,过点C做垂直于x轴,垂足为E,则,再分别求解 利用的面积的面积的面积,从而可得答案.
【详解】解: ,,
过点A做垂直于x轴,垂足为D,则,
过点C做垂直于x轴,垂足为E,则,
的面积的面积的面积,
,,,,
,,,
∴的面积,
的面积,
∴的面积.
故选A.
【点睛】本题考查的是坐标与图形,三角形面积的计算,掌握以上知识是解题的关键.
10.A
【分析】观察点的坐标变化发现每个点的横坐标与次数相等,纵坐标是个数一个循环,进而可得经过第次运动后,动点P的坐标.
【详解】解:观察点的坐标变化可知:
第1次从原点运动到点,
第2次接着运动到点,
第3次接着运动到点,
第4次接着运动到点,
第5次接着运动到点,
…
按这样的运动规律,
发现每个点的横坐标与次数相等,
纵坐标是个数一个循环,
所以,
所以经过第次运动后,
动点P的坐标是.
故选:A.
【点睛】本题考查了规律型 点的坐标,解决本题的关键是观察点的坐标变化寻找规律.
11.
【分析】根据有序数对的第一个数表示排数,第二个数表示座数解答.
【详解】解:∵有序实数对表示四排三列,
∴一排五列可用有序实数对表示为:.
故答案为:.
【点睛】本题考查了坐标确定位置,理解有序数对的两个数的实际意义是解题的关键.
12.二
【分析】根据非负数的性质得到,的值,得到点的坐标,即可知道点所在的象限.
【详解】解:根据题意得,
,,
,,
,
点在第二象限,
故答案为:二.
【点睛】本题考查了非负数的性质,点的坐标,掌握两个非负数的和为,则这两个非负数分别等于是解题的关键.
13.
【分析】根据第二象限坐标特征为得到,求不等式组的解集即可.
【详解】因为点在第二象限,
所以,
解得.
故答案为:.
【点睛】本题考查了坐标与象限的关系,转化为不等式组问题求解是解题的关键.
14.或
【分析】根据平行于x轴的直线上的点纵坐标都相等,得出点B的纵坐标,再根据,即可得出点B的坐标.
【详解】解:∵轴,A点的坐标为,
∴点B的纵坐标为2,
∵,
∴点B的横坐标为或,
∴B的坐标为或.
故答案为:或.
【点睛】本题考查了坐标与图形性质,熟练掌握平面直角坐标系内点的坐标特征是解题的关键.
15.2或6##6或2
【分析】分点在一、三象限的角平分线上和二、四象限的角平分线上两种情况讨论即可.
【详解】解:当点A在一、三象限的角平分线上时,
∴
∴a= 2
当点A在二、四象限的角平分线上时,
∴
∴a= 6
故答案为:2或6
【点睛】此题主要考查了点的坐标,正确得出横纵坐标的关系是解题关键.
16.a>3
【分析】根据点A(2a+4,6﹣2a)在第四象限和第四象限点的坐标的特点,可以得到关于a的不等式组,从而可以得到a的取值范围.
【详解】解:∵点A(2a+4,6﹣2a)在第四象限,
∴,
解得a>3,
故答案为:a>3.
【点睛】本题考查解一元一次不等式组、点的坐标,解答本题的关键是明确第四象限点的坐标的符号是(+, ),列出相应的不等式组.
17.11
【分析】过点B作BD⊥x轴于D,则,根据梯形和三角形的面积公式代入数值求解即可.
【详解】过点B作BD⊥x轴于D,则点D的坐标为,
所以.
故答案为:11
【点睛】本题考查平面直角坐标系中图形面积的求法,灵活运用割补法是解题的关键.
18.
【分析】先根据条件,算出每个正方形的边长,再根据坐标的变换计算出点A的坐标即可.
【详解】解:设正方形的边长为,
则由题设条件可知:
解得:
点A的横坐标为:,点A的纵坐标为:
故点A的坐标为.
故答案为:.
【点睛】本题考查了平面直角坐标系,根据图形和点的特征计算出点的坐标是解题的关键.
19.(1)见解析;(2);(3)3.5.
【分析】(1)根据坐标与象限的关系,建立直角坐标系,将、表示在直角坐标系中即可;
(2)根据坐标与象限的关系,点在第一象限,横坐标、纵坐标均为正数,据此解题
(3)由割补法解题,的面积等于梯形面积减去两个直角三角形面积即可解题.
【详解】(1)如图所示,即为所求
(2)点在第一象限,横坐标、纵坐标均为正数,
故答案为:;
(3)
故答案为:3.5.
【点睛】本题考查坐标与图形,是重要考点,难度较易,掌握相关知识是解题关键.
20.(1)2
(2)5或-1
(3)
【分析】(1)若点在y轴上,则M的横坐标为0,即2-m=0,即可得答案;
(2)根据点M到y轴的距离是3,可得横坐标的绝对值为3,即可求解.
(3)若点M在第一、三象限的角平分线上,则点M的横纵坐标相等,即2-m=1+2m,计算即可.
【详解】(1)解:∵点M(2-m,1+2m)在y轴上,
∴2-m=0,
∴m=2;
(2)∵点M到y轴的距离是3,
∴|2-m|=3,
解得:m=5或-1;
(3)∵点M(2-m,1+2m)在第一、三象限的角平分线上,
∴2-m=1+2m,
∴m=.
【点睛】本题考查了一元一次方程的解法,点与坐标的对应关系,坐标轴上的点的特征,各个象限的点的特征,第一、三象限的角平分线上的点的特征,解题的关键是掌握相关性质.
21.(1)<m<3;
(2)点P的坐标为(3,﹣2)或(﹣3,﹣5).
【分析】(1)直接利用第四象限内点的坐标特点分析得出答案;
(2)利用点P到y轴的距离为3,得出m的值.
【详解】(1)解:由题知,
解得:;
(2)解:由题知|2m+1|=3,
解得m=1或m=﹣2.
当m=1时,得P(3,﹣2);
当m=﹣2时,得P(﹣3,﹣5).
综上,点P的坐标为(3,﹣2)或(﹣3,﹣5).
【点睛】此题主要考查了点的坐标,熟练掌握点在各象限内的特点以及点到坐标轴的距离是解题关键.
22.(1)见解析
(2)8
【分析】(1)根据平面直角坐标系描出点的坐标;
(2)根据,求面积即可求解.
【详解】(1)解:如图所示:点A、B、C、D为所描的点.
(2)方法一:如图所示,作长方形EFGH:
则有
方法二:如图所示,将四边形ABCD分割为△ABP、△BCQ、△CMD、
△AND和正方形PQMN,
则有
.
【点睛】本题考查了坐标与图形,数形结合是解题的关键.
23.(1)A(8,6);(2)
【分析】(1)根据矩形的面积列方程即可得到结论;
(2)由S△AEF<S△CDF,得到S四边形ABOC>S梯形DOBE,解不等式即可得到结论.
【详解】解:(1)∵ AB⊥x轴, AC⊥y轴,
∴四边形ABOC是矩形,
∵AC =4m ,AB=3m,四边形ABOC的面积为48,
∴4m×3m=48,
∴m=2或-2,
∵点A在第一象限,
∴m=2,
∴A(8,6);
(2)由题意知,OD=t,AE=2t,
∵S△AEF<S△CDF,
∴S△CDF+S五边形ABODF>S△AEF+S五边形ABODF,即S四边形ABOC>S梯形DOBE,
∴,
∴,
∴t的取值范围是.
【点睛】本题考查了坐标与图形的性质,三角形和梯形的面积的计算,用数形结合的思想解决问题是解题的关键.
24.(1)C
(2)①(0,3),(3,0);②或;③分类讨论(答案不唯一);
【分析】(1)根据数学的历史知识判断即可;
(2)分别作出点A、B、C平移后的坐标,再连接相应顶点;①根据坐标的定义写出坐标即可;②根据坐标特征可得的底边上的高为3,求得底边的长,再分别讨论点D在左边和右边即可;③根据②的解答方法判断即可;
【详解】(1)解:最早引入坐标系,用代数方法研究几何图形的数学家是:笛卡尔;
故选: C.
(2)解:如图,点A、B、C分别向下平移1个单位长度,再向右平移2个单位长度得到点A1、B1、C1,连接相应顶点则即为所求;
①由图象可得的坐标,的坐标;
故答案为:(0,3),(3,0);
② ∵D点在x轴上,的面积等于3,的坐标,
∴底边上的高为3,
∴的长度为2,
∵的坐标,
∴当点D在左边时,D点坐标为(1,0),当点D在右边时,D点坐标为(5,0);
③∵根据点D在点左边和右边分别讨论,
∴利用了分类讨论的思想;
故答案为:分类讨论(答案不唯一).
【点睛】本题考查了平面直角坐标系,坐标的定义,坐标的规律等知识;根据D点位置分类讨论是解题关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列表述中,能确定物体位置的是( )
A.万达影城1号厅2排 B.温泉南路
C.南偏西 D.东经,北纬
2.已知点P在第四象限,且到x轴的距离是2,到y轴的距离是7,则点P的坐标为( )
A. B. C. D.
3.点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )
A.(3, 3) B.(3,-3) C.(6,-6) D.(3,3)或
4.点A(m+3,m+1)在y轴上,则点A的坐标为( )
A.(0,-2) B.(2,0) C.(4,y) D.(0,-4)
5.如图,小手盖住的点的坐标可能为( )
A. B. C. D.
6.如图,已知正方形,顶点,,,规定“把正方形先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2019次变换后,正方形的对角线交点M的坐标变为( )
A. B. C. D.
7.在平面直角坐标系内,点P(,)在第四象限,则的取值范围是( )
A. B. C. D.
8.下列说法正确的是( )
A.若点,则点A到x轴的距离为3 B.平行于y轴的直线上所有点的纵坐标都相同
C.与表示两个不同的点 D.若点在x轴上,则
9.如图在平面直角坐标系中,点A、B、C的坐标分别为,,,则的面积是( )
A.5 B.10 C.75 D.15
10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点,第次接着运动到点,第次接着运动到点,…,按这样的运动规律,经过第次运动后,动点的坐标是( )
A. B. C. D.
二、填空题
11.若四排三列用有序实数对来表示,那么表示一排五列的有序实数对为 .
12.已知,则在 象限.
13.点在第二象限,则x的取值范围是 .
14.已知轴,A点的坐标为,并且,则B的坐标为 .
15.已知点在象限角平分线上,则的值为 .
16.在平面直角坐标系中,点A(2a+4,6﹣2a)在第四象限,则a的取值范围是 .
17.如图所示,在平面直角坐标系中,点,,,则四边形ABCO的面积为 .
18.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点、的坐标分别为、,则顶点的坐标为 .
三、解答题
19.如图,用表示点的位置,用表示点的位置.
(1)画出直角坐标系.
(2)点的坐标为______.
(3)的面积为______.
20.在平面直角坐标系中,已知点.
(1)若点M在y轴上,求m的值;
(2)若点M到y轴的距离是3,求m的值;
(3)若点M在第一、三象限的角平分线上,求m的值.
21.已知平面直角坐标系中有一点P(2m+1,m﹣3).
(1)若点P在第四象限,求m的取值范围;
(2)若点P到y轴的距离为3,求点P的坐标.
22.已知平面直角坐标系内有4个点:A(0,2),B(-2,0),C(1,-1),D(3,1).
(1)在平面直角坐标系中描出这4个点;
(2)顺次连接A、B、C、D组成四边形ABCD,请用两种方法求出四边形ABCD的面积.
23.如图,平面直角坐标系中,点A在第一象限,AB⊥x轴于B,AC⊥y轴于C,A(4m,3m),且四边形ABOC的面积为48.
(1)如图①,求A点的坐标;
(2)如图②,点D从O出发以每秒1个单位的速度沿y轴正半轴运动,同时点E从A出发,以每秒2个单位的速度沿射线BA运动,DE交线段AC于F,设运动的时间为t,当S△AEF<S△CDF时,求t的取值范围.
24.平面直角坐标系是由原点重合且互相垂直的两条数轴构成的,它是沟通代数与几何的桥梁,是非常重要的数学工具.
(1)最早引入坐标系,用代数方法研究几何图形的数学家是( )
A.祖冲之 B.刘徽 C.笛卡尔 D.欧几里得
(2)在数学活动课上,老师与同学们一起探究如下问题:
在平面直角坐标系中的位置如图,已知点的坐标为.把向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的.
①写出点的坐标_________,的坐标_________;
②在轴上找一点,使的面积等于3,求满足条件的点的坐标;
③在解决问题②时用到的数学思想是__________________(填一个即可)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据确定位置的有序数对有两个数解答.
【详解】解:在平面直角坐标系中,要用两个数据才能表示一个点的位置,纵观各选项,只有东经,北纬能确定物体的位置,
故选:D
【点睛】本题考查了坐标确定位置,理解在平面直角坐标系中,要用两个数据才能表示一个点的位置是解题的关键.
2.A
【分析】根据第四象限坐标特征,及点P分别到x轴和y轴的距离可得答案.
【详解】解:点P在第四象限,到x轴的距离是2,到y轴的距离是7,
点P横坐标为7,纵坐标为-2,
点P的坐标,
故选:A.
【点睛】此题考查了四象限的点坐标特征,掌握第四象限中的点是解题关键.
3.D
【分析】由点P到两坐标轴的距离相等,建立绝对值方程再解方程即可得到答案.
【详解】解: 点P到两坐标轴的距离相等,
或
当时,
当
综上:的坐标为:或
故选D.
【点睛】本题考查的是平面直角坐标系内点的坐标特点,点到坐标轴的距离与坐标的关系,一元一次方程的解法,掌握以上知识是解题的关键.
4.A
【分析】根据点在y轴上,点的横坐标为0即可求解.
【详解】解:由题意知,点A(m+3,m+1)在y轴上,则该点的横坐标为0,
∴m+3=0,
∴m=-3,代入,此时点A(0,-2),
故选:A.
【点睛】本题考查了平面直角坐标系中点的特征,熟练掌握平面直角坐标系中坐标轴上点的坐标特征是解决本题的关键.
5.D
【分析】根据各象限内点的坐标特征解题,四个象限的符号特征为:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-) .
【详解】小手盖住的是第四象限的点,其点坐标特征为:横坐标为正数,纵坐标为负数,
故选:D.
【点睛】本题考查象限及点的坐标的有关性质等知识,是基础考点,难度较易,掌握相关知识是解题关键.
6.C
【分析】依次按要求变化后写出坐标,得出坐标与变化次数n的关系即可.
【详解】解:∵正方形,顶点,,,
∴正方形的对角线交点M的坐标为,
∵把正方形先沿x轴翻折,再向左平移1个单位长度为一次变换,
∴第一次变换后点M的坐标为,第二次变换后点M的坐标为,第三次变换后点M的坐标为,第四次变换后点M的坐标为
可以发现点n次后,当n为偶数,点M的坐标为,
当n是奇数,点M的坐标为,
∴连续经过2019次变换后,正方形的对角线交点M的坐标变为,
故选:C.
【点睛】本题主要考查坐标系上点翻折,平移后点的坐标,依据要求正确求出变化后点的坐标是解题关键.
7.C
【详解】解:点P(,)在第四象限,根据第四象限点的坐标特征,
则
解得:
故选C.
8.C
【分析】根据平面直角坐标系内点的坐标特点分别进行判断,即可得出结论.
【详解】解:A、若点,则点A到y轴的距离为3;故此选项说法错误,不符合题意;
B、平行于y轴的直线上所有点的横坐标都相同;故此选项说法错误,不符合题意;
C、与表示两个不同的点;故此选项说法正确,符合题意;
D、若点在x轴上,则;故此选项说法错误,不符合题意.
故选:C.
【点睛】本题考查了平面直角坐标系,解题的关键是熟练掌握平面直角坐标系内点的坐标特点是解题的关键.
9.A
【分析】过点A做垂直于x轴,垂足为D,则,过点C做垂直于x轴,垂足为E,则,再分别求解 利用的面积的面积的面积,从而可得答案.
【详解】解: ,,
过点A做垂直于x轴,垂足为D,则,
过点C做垂直于x轴,垂足为E,则,
的面积的面积的面积,
,,,,
,,,
∴的面积,
的面积,
∴的面积.
故选A.
【点睛】本题考查的是坐标与图形,三角形面积的计算,掌握以上知识是解题的关键.
10.A
【分析】观察点的坐标变化发现每个点的横坐标与次数相等,纵坐标是个数一个循环,进而可得经过第次运动后,动点P的坐标.
【详解】解:观察点的坐标变化可知:
第1次从原点运动到点,
第2次接着运动到点,
第3次接着运动到点,
第4次接着运动到点,
第5次接着运动到点,
…
按这样的运动规律,
发现每个点的横坐标与次数相等,
纵坐标是个数一个循环,
所以,
所以经过第次运动后,
动点P的坐标是.
故选:A.
【点睛】本题考查了规律型 点的坐标,解决本题的关键是观察点的坐标变化寻找规律.
11.
【分析】根据有序数对的第一个数表示排数,第二个数表示座数解答.
【详解】解:∵有序实数对表示四排三列,
∴一排五列可用有序实数对表示为:.
故答案为:.
【点睛】本题考查了坐标确定位置,理解有序数对的两个数的实际意义是解题的关键.
12.二
【分析】根据非负数的性质得到,的值,得到点的坐标,即可知道点所在的象限.
【详解】解:根据题意得,
,,
,,
,
点在第二象限,
故答案为:二.
【点睛】本题考查了非负数的性质,点的坐标,掌握两个非负数的和为,则这两个非负数分别等于是解题的关键.
13.
【分析】根据第二象限坐标特征为得到,求不等式组的解集即可.
【详解】因为点在第二象限,
所以,
解得.
故答案为:.
【点睛】本题考查了坐标与象限的关系,转化为不等式组问题求解是解题的关键.
14.或
【分析】根据平行于x轴的直线上的点纵坐标都相等,得出点B的纵坐标,再根据,即可得出点B的坐标.
【详解】解:∵轴,A点的坐标为,
∴点B的纵坐标为2,
∵,
∴点B的横坐标为或,
∴B的坐标为或.
故答案为:或.
【点睛】本题考查了坐标与图形性质,熟练掌握平面直角坐标系内点的坐标特征是解题的关键.
15.2或6##6或2
【分析】分点在一、三象限的角平分线上和二、四象限的角平分线上两种情况讨论即可.
【详解】解:当点A在一、三象限的角平分线上时,
∴
∴a= 2
当点A在二、四象限的角平分线上时,
∴
∴a= 6
故答案为:2或6
【点睛】此题主要考查了点的坐标,正确得出横纵坐标的关系是解题关键.
16.a>3
【分析】根据点A(2a+4,6﹣2a)在第四象限和第四象限点的坐标的特点,可以得到关于a的不等式组,从而可以得到a的取值范围.
【详解】解:∵点A(2a+4,6﹣2a)在第四象限,
∴,
解得a>3,
故答案为:a>3.
【点睛】本题考查解一元一次不等式组、点的坐标,解答本题的关键是明确第四象限点的坐标的符号是(+, ),列出相应的不等式组.
17.11
【分析】过点B作BD⊥x轴于D,则,根据梯形和三角形的面积公式代入数值求解即可.
【详解】过点B作BD⊥x轴于D,则点D的坐标为,
所以.
故答案为:11
【点睛】本题考查平面直角坐标系中图形面积的求法,灵活运用割补法是解题的关键.
18.
【分析】先根据条件,算出每个正方形的边长,再根据坐标的变换计算出点A的坐标即可.
【详解】解:设正方形的边长为,
则由题设条件可知:
解得:
点A的横坐标为:,点A的纵坐标为:
故点A的坐标为.
故答案为:.
【点睛】本题考查了平面直角坐标系,根据图形和点的特征计算出点的坐标是解题的关键.
19.(1)见解析;(2);(3)3.5.
【分析】(1)根据坐标与象限的关系,建立直角坐标系,将、表示在直角坐标系中即可;
(2)根据坐标与象限的关系,点在第一象限,横坐标、纵坐标均为正数,据此解题
(3)由割补法解题,的面积等于梯形面积减去两个直角三角形面积即可解题.
【详解】(1)如图所示,即为所求
(2)点在第一象限,横坐标、纵坐标均为正数,
故答案为:;
(3)
故答案为:3.5.
【点睛】本题考查坐标与图形,是重要考点,难度较易,掌握相关知识是解题关键.
20.(1)2
(2)5或-1
(3)
【分析】(1)若点在y轴上,则M的横坐标为0,即2-m=0,即可得答案;
(2)根据点M到y轴的距离是3,可得横坐标的绝对值为3,即可求解.
(3)若点M在第一、三象限的角平分线上,则点M的横纵坐标相等,即2-m=1+2m,计算即可.
【详解】(1)解:∵点M(2-m,1+2m)在y轴上,
∴2-m=0,
∴m=2;
(2)∵点M到y轴的距离是3,
∴|2-m|=3,
解得:m=5或-1;
(3)∵点M(2-m,1+2m)在第一、三象限的角平分线上,
∴2-m=1+2m,
∴m=.
【点睛】本题考查了一元一次方程的解法,点与坐标的对应关系,坐标轴上的点的特征,各个象限的点的特征,第一、三象限的角平分线上的点的特征,解题的关键是掌握相关性质.
21.(1)<m<3;
(2)点P的坐标为(3,﹣2)或(﹣3,﹣5).
【分析】(1)直接利用第四象限内点的坐标特点分析得出答案;
(2)利用点P到y轴的距离为3,得出m的值.
【详解】(1)解:由题知,
解得:;
(2)解:由题知|2m+1|=3,
解得m=1或m=﹣2.
当m=1时,得P(3,﹣2);
当m=﹣2时,得P(﹣3,﹣5).
综上,点P的坐标为(3,﹣2)或(﹣3,﹣5).
【点睛】此题主要考查了点的坐标,熟练掌握点在各象限内的特点以及点到坐标轴的距离是解题关键.
22.(1)见解析
(2)8
【分析】(1)根据平面直角坐标系描出点的坐标;
(2)根据,求面积即可求解.
【详解】(1)解:如图所示:点A、B、C、D为所描的点.
(2)方法一:如图所示,作长方形EFGH:
则有
方法二:如图所示,将四边形ABCD分割为△ABP、△BCQ、△CMD、
△AND和正方形PQMN,
则有
.
【点睛】本题考查了坐标与图形,数形结合是解题的关键.
23.(1)A(8,6);(2)
【分析】(1)根据矩形的面积列方程即可得到结论;
(2)由S△AEF<S△CDF,得到S四边形ABOC>S梯形DOBE,解不等式即可得到结论.
【详解】解:(1)∵ AB⊥x轴, AC⊥y轴,
∴四边形ABOC是矩形,
∵AC =4m ,AB=3m,四边形ABOC的面积为48,
∴4m×3m=48,
∴m=2或-2,
∵点A在第一象限,
∴m=2,
∴A(8,6);
(2)由题意知,OD=t,AE=2t,
∵S△AEF<S△CDF,
∴S△CDF+S五边形ABODF>S△AEF+S五边形ABODF,即S四边形ABOC>S梯形DOBE,
∴,
∴,
∴t的取值范围是.
【点睛】本题考查了坐标与图形的性质,三角形和梯形的面积的计算,用数形结合的思想解决问题是解题的关键.
24.(1)C
(2)①(0,3),(3,0);②或;③分类讨论(答案不唯一);
【分析】(1)根据数学的历史知识判断即可;
(2)分别作出点A、B、C平移后的坐标,再连接相应顶点;①根据坐标的定义写出坐标即可;②根据坐标特征可得的底边上的高为3,求得底边的长,再分别讨论点D在左边和右边即可;③根据②的解答方法判断即可;
【详解】(1)解:最早引入坐标系,用代数方法研究几何图形的数学家是:笛卡尔;
故选: C.
(2)解:如图,点A、B、C分别向下平移1个单位长度,再向右平移2个单位长度得到点A1、B1、C1,连接相应顶点则即为所求;
①由图象可得的坐标,的坐标;
故答案为:(0,3),(3,0);
② ∵D点在x轴上,的面积等于3,的坐标,
∴底边上的高为3,
∴的长度为2,
∵的坐标,
∴当点D在左边时,D点坐标为(1,0),当点D在右边时,D点坐标为(5,0);
③∵根据点D在点左边和右边分别讨论,
∴利用了分类讨论的思想;
故答案为:分类讨论(答案不唯一).
【点睛】本题考查了平面直角坐标系,坐标的定义,坐标的规律等知识;根据D点位置分类讨论是解题关键.
答案第1页,共2页
答案第1页,共2页
