专题7.11平面直角坐标系 存在性问题 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题7.11平面直角坐标系 存在性问题 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 00:00:00 | ||
图片预览




文档简介
专题7.11 平面直角坐标系(存在性问题)(专项练习)
存在性问题涉及的知识面广,综合性强,充满生机,要求同学们有扎实的基础知识和熟练的基本技能,因此存在性问题已成为近几年中考数学命题的一个热点。
解决存在性问题一般套路:假设存在→推理论证→得岀结论。简单地说就是若能导出合理的结果,就做出“存在”的判断,导出矛盾,就做出不存在的判断。
具体来说,我们可以归纳出三种解决存在性问题的解题策略:
1、直接求解法
直接从已知条件入手,逐步试探求出满足条件的对象,使问题得到解决。
2、假设求解法
先假设结论存在,再从已知条件和定义定理公理出发进行演绎推理若得到和题意相容的结论,则假设成立结论也存在;否则假设不成立结论不存在。
3、反证法
反证法是证明否定型存在性问题的主要方,特别是在无限个候选对象中证明某种数学对象不存在时,逐一淘汰的方法几乎不能实行,更需要使用反证法。
一、解答题
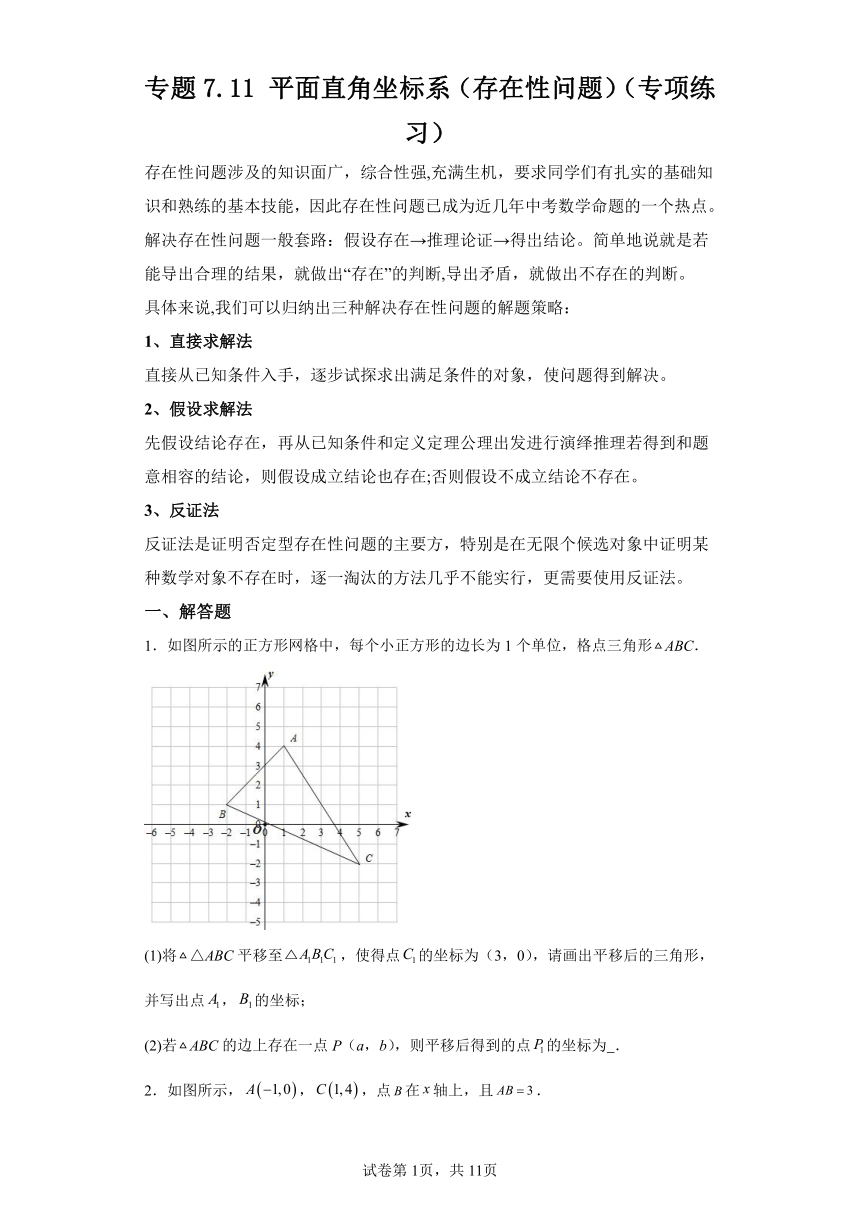
1.如图所示的正方形网格中,每个小正方形的边长为1个单位,格点三角形ABC.
(1)将△ABC平移至,使得点的坐标为(3,0),请画出平移后的三角形,并写出点,的坐标;
(2)若ABC的边上存在一点P(a,b),则平移后得到的点的坐标为 .
2.如图所示,,,点在轴上,且.
(1)求点的坐标;
(2)求三角形的面积;
(3)在轴上是否存在点,使以、、三点为顶点的三角形的面积为?若存在,请直接写出点的坐标;若不存在,请说明理由.
3.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接AA1,AO,A1O,求△AOA1的面积.
(4)连接BA1,在y轴上是否存在点Q,使得三角形QBA1的面积为8,若存在,求出点Q的坐标;若不存在,请说明理由.
4.如图,在平面直角坐标系中,已知,,三点,其中、、满足关系式,
(1)求、、的值;
(2)如果在第二象限内有一点,请用含的式子表示四边形的面积;
(3)在(2)的条件下,是否存在点,使四边形的面积与的面积相等?若存在,求出点的坐标;若不存在,请说明理由.
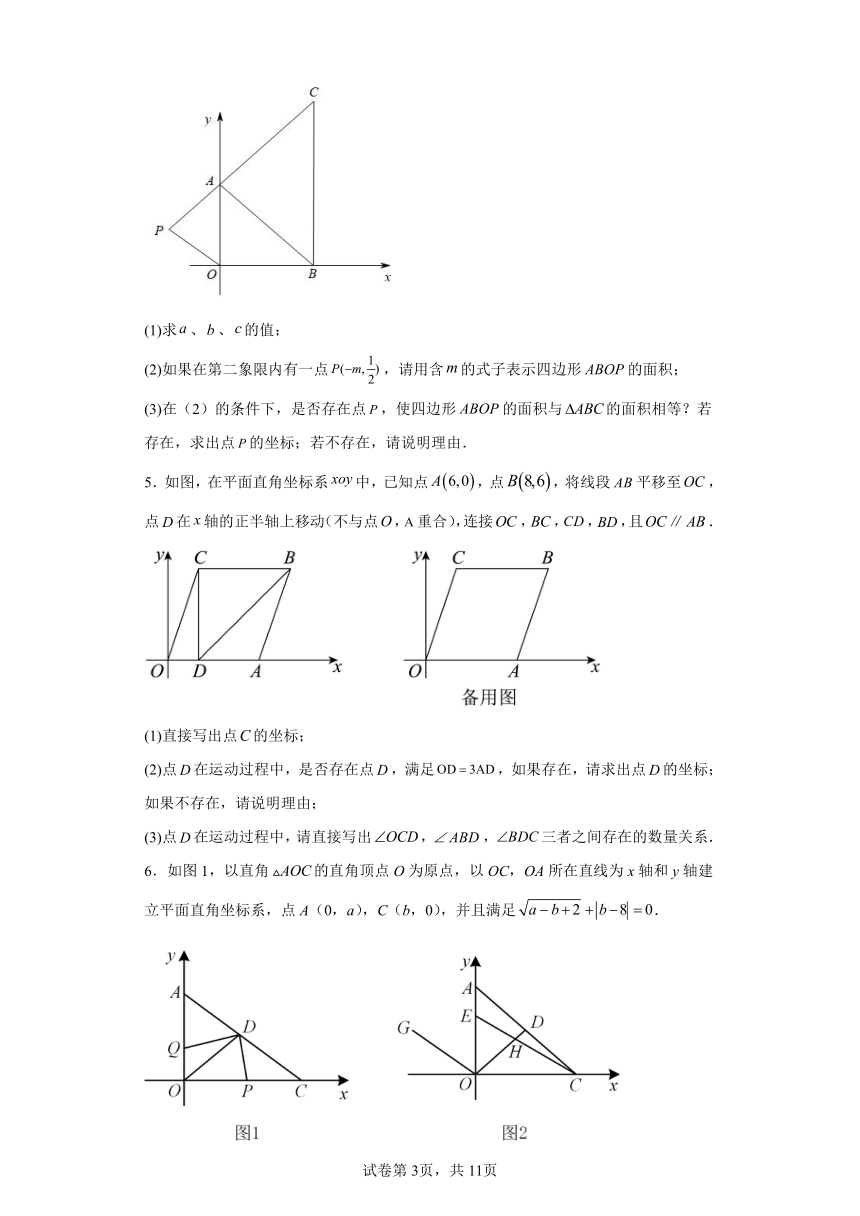
5.如图,在平面直角坐标系中,已知点,点,将线段平移至,点在轴的正半轴上移动(不与点,重合),连接,,,,且.
(1)直接写出点的坐标;
(2)点在运动过程中,是否存在点,满足,如果存在,请求出点的坐标;如果不存在,请说明理由;
(3)点在运动过程中,请直接写出,,三者之间存在的数量关系.
6.如图1,以直角的直角顶点O为原点,以OC,OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0),并且满足.
(1)直接写出点A,点C的坐标;
(2)如图1,坐标轴上有两动点P,Q同时出发,点P从点C出发沿x轴负方向以每秒2个单位长度的速度匀速运动,点Q从点O出发沿y轴正方向以每秒1个单位长的速度匀速运动,当点P到达点O整个运动随之结束;点D的坐标是(4,3),设运动时间为t秒.是否存在t,使得与的面积相等?若存在,求出t的值;若不存在,说明理由;
(3)如图2,在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且OA平分∠DOG,点E是线段OA上一动点,连接CE交OD于点H,当点E在OA上运动的过程中,
①说明的理由
②直接写出∠DOG,∠OHC,∠ACE之间的数量关系.
7.如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式,.
(1)求a、b、c的值:
(2)如果在第二象限内有一点,请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
8.如图在平面直角坐标系内,、分别在轴、轴正半轴上,且,点的横坐标为;
(1)当时,求点坐标;
(2)将线段左右平移,使得点落在坐标原点,此时,点落在点的位置.
请直接写出平移的方向和距离以及点的坐标;(用含的代数式表示)
轴上是否存在点,使得面积是面积的两倍,如果存在,直接写出点的坐标(用含的代数式表示),如果不存在,请说明理由.
9.如图,在平面直角坐标系中,,,且满足,过点作直线轴,点是直线上一动点,连接,过点作交轴于点,,分别平分,.
(1)填空:_______,______;
(2)在点的运动过程中,的度数是否变化?若不变,请求出它的度数;若变化,请说明理由;
(3)若点的纵坐标为,在轴上是否存在点,使得的面积和的面积相等?若存在,求出点坐标;若不存在,请说明理由.
10.如图,网格中每个小正方形的边长均为1个单位长度,已知A(﹣2,1),B(﹣2,﹣1),C(0,1).
(1)请在图中所示的平面直角坐标系中作出△ABC;
(2)把△ABC平移到△A1B1C1,使点A的对应点为A1的坐标为(0,﹣2),请你作出△A1B1C1,(点B1,C1分别是B,C的对应点),写出点B1,C1的坐标.
(3)y轴上是否存在点M,使,若存在,求出点M的坐标,不存在请说明理由.
11.综合与探究:如图,在平面直角坐标系中,点,的坐标分别为,且、满足,将线段沿轴方向向右平移个单位后得到线段,连接.点从原点出发,以每秒个单位的速度沿匀速运动,设运动时间为秒.
(1)点的坐标为______,点的坐标为______;
(2)当时,试求四边形的面积;
(3)是否存在这样的值,使四边形的面积等于?若存在,请直接写出的值;若不存在,请说明理由.
12.如图1,在平面直角坐标系中,,且满足,过C作轴于B.
(1)求的面积;
(2)若过B作交y轴于D,且AE,DE分别平分,如图2,求的度数;
(3)在y轴上存在点P使得和的面积相等,请直接写出P点坐标.
13.如图,点在第一象限,点,点,且、满足:.
(1)求的面积;
(2)在坐标轴上是否存在一点(不和点重合),使?若存在,请直接写出所有符合题意的点的坐标,并把求其中一个点的坐标的过程写出来.
14.如图1,在平面直角坐标系中,,,,且
(1)求,的值.
(2)①在轴的正半轴上存在一点,使,求点的坐标;
②在坐标轴的其它位置是否存在点,使仍然成立,若存在,请直接写出符合条件的点的坐标.
(3)如图2,过点作轴交轴于点,点为线段延长线上一动点,连接,平分,.当点运动时,的值是否会改变?若不变,求其值;若改变,说明理由.
15.如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足,现同时将点A,B分别向上平移3个单位长度,再向右平移1个单位长度,得到点A,B的对应点D,C,连接AD,BC,CD.
(1)求a,b的值,并直接写出点A,点B,点C,点D的坐标;
(2)如图2,点P是线段DC上的一个动点,连接PA,PB,当点P在线段DC上移动时,的面积是否变化?若不变,请求出的面积;若变化,请说明理由.
(3)在x轴上是否存在一点M,使的面积与的面积相等?若存在,请直接写出点M的坐标;若不存在,试说明理由.
16.如图,在下面直角坐标系中,已知,,三点,其中、、满足关系式和.
(1)求、、的值;
(2)如果在第二象限内有一点,请用含的式子表示四边形的面积;
(3)在(2)的条件下,是否存在点,使得四边形的面积与的面积相等?若存在,求出点的坐标;若不存在,请说明理由.
17.在平面直角坐标系中,点,的坐标分别为,,现将线段先向上平移3个单位,再向右平移1个单位,得到线段,连接,.
(1)如图1,求点,的坐标及四边形的面积;
(2)如图1,在轴上是否存在点,连接,,使?若存在这样的点,求出点的坐标;若不存在,试说明理由;
(3)如图2,点为与轴交点,在直线上是否存在点,连接,使?若存在这样的点,直接写出点的坐标;若不存在,试说明理由;
18.如图,在平面直角坐标系中,已知,,其中,满足.
(1)填空:______,________;
(2)若存在一点,点M到x轴距离_______,到y轴距离_______,求的面积(用含m的式子表示);
(3)在(2)条件下,当时,在y轴上有一点P,使得的面积与的面积相等,请求出点P的坐标.
19.如图,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)若线段与轴交于点,在轴上是否存在点,使得三角形和三角形的面积相等,若存在,求出点坐标;若不存在,请说明理由;
20.在直角坐标系中,已知线段,点A的坐标为,点B的坐标为,如图1所示.
(1)平移线段到线段,使点A的对应点为D,点B的对应点为C,若点C的坐标为,求点D的坐标;
(2)平移线段到线段,使点C在y轴的正半轴上,点D在第二象限内,连接,,如图2所示.若(表示三角形的面积),求点C、D的坐标.
(3)在(2)的条件下,在y轴上是否存在一点P,使(表示三角形的面积)?若存在,求出点P的坐标;若不存在,请说明理由.
21.如图,在平面直角坐标系中,已知,点为第三象限内一点.
(1)若到两坐标轴的距离相等,,且,则点坐标为______.
(2)若为,请用含的式子表示的面积.
(3)在(2)条件下,当时,在轴上有点,使得的面积是的面积的2倍,请直接写出点的坐标.
22.如图1 ,在平面直角坐标系中,点A、B的坐标分别为,,现同时将A、B向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接、、.
(1)写出C、D的坐标并求出四边形的面积.
(2)在x 轴上 是否存在一点F,使得三角形的面积是三角形面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图 2、3、4,点 P 是直线上的一个动点,连接、,当点P在直线上运动时,请直接写出与、的数量关系.
23.如图,在平面直角坐标系中,四边形各顶点的坐标分别为
(1)求此四边形的面积.
(2)在坐标轴上,你能否找到一点P,使?若能,求出P点坐标;若不能,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)图见解析,(-1,6),(-4,3)
(2)(a-2,b+2)
【分析】(1)先由点的坐标为(3,0)判断出平移的方式,然后画出图形,再写出,的坐标;
(2)根据(1)中平移的方式解答即可.
【详解】(1)解:∵C(5,-2),(3,0),
∴三角形先向左平移了2个单位,又向上平移了2个单位,
如图,即为所求,
(-1,6),(-4,3).
(2)解:∵三角形先向左平移了2个单位,又向上平移了2个单位,
则三角形边上的点P(a,b)平移后得到点(a-2,b+2).
故答案为:(a-2,b+2).
【点睛】本题考查了坐标与图形变换-平移,判断平移的方式以及根据平移的方式确定点的坐标,由点C平移后的坐标判断平移的方式是解答本题的关键.
2.(1)或;
(2);
(3)存在,或
【分析】(1)分点在点的左边和右边两种情况解答;
(2)利用三角形的面积公式列式计算即可得解;
(3)利用三角形的面积公式列式求出点到轴的距离,然后分两种情况写出点的坐标即可.
【详解】(1)如图,
当点在点的右边时,,
当点在点的左边时,,
所以的坐标为或;
(2)的面积,
答:的面积为;
(3)设点到轴的距离为,
则,
解得,
当点在轴正半轴时,,
当点在轴负半轴时,,
综上所述,点的坐标为或
【点睛】本题考查了点的坐标的确定,三角形的面积公式,分类讨论,坐标轴上两点间的距离公式等有关知识;能求出符合条件的点的坐标是解此题的关键.
3.(1)(3,1),(1,﹣1),(4,﹣2);
(2)图形见解析;
(3)6
(4)Q点的坐标为(0,﹣1)或(0,3).
【分析】(1)利用P点和的坐标特征得到平移的方向与距离,然后利用此平移规律写出点,,的坐标;
(2)利用点,,的坐标描点即可;
(3)用一个矩形的面积分别减去三个直角三角形的面积,即可计算的面积;
(4)设Q(0,t),利用三角形面积公式得到×8×|t﹣1|=8,然后解方程求出t得到Q点的坐标.
【详解】(1)由P点和的坐标特征可得:平移是向右平移6个单位长度,再向下平移2个单位长度,此平移,点A平移后的坐标为(3,1),点B平移后的坐标为(1,﹣1),点C平移后的坐标为(4,﹣2);
故(3,1),(1,﹣1),(4,﹣2);
(2)如图,为所作;
(3)的面积=6×3﹣×3×3﹣×3×1﹣×6×2
=
=18﹣12
=6;
(4)设Q(0,t),
∵B(﹣5,1),(3,1),
∴B=3﹣(﹣5)=8,
∵的面积为8,
∴×8×|t﹣1|=8,解得t=﹣1或t=3,
∴Q点的坐标为(0,﹣1)或(0,3).
【点睛】本题考查了作图﹣平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形;解答本题关键是确定平移.
4.(1),,
(2)
(3)存在,
【分析】(1)根据几个非负数和的性质得到,分别解一元一次方程得到;
(2)根据三角形的面积公式和四边形的面积= 进行计算;
(3)可求,是已知量,根据题意,列出方程求解即可.
【详解】(1)由已知,
可得:
∴,,;
(2)由(1)知,a=2,b=3,
∴A(0,2),B(3,0),
∴OA=2,OB=3,
,,
(3)由(1)知,a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴BC=4,
∴,
∵四边形ABOP的面积与△ABC的面积相等,
∴S=6,
由(2)知,S=m+3,
∴m+3=6,
∴m=3,
∴
【点睛】本题考查了坐标与图形性质:利用坐标计算线段的长度和判断线段与坐标轴的位置关系.也考查了三角形的面积公式.
5.(1)
(2)或
(3)当点在之间时,;当点在右侧时,
【分析】(1)根据平移的性质得,,即可得出点的坐标;
(2)根据,由点的位置进行分类讨论即可得出答案;
(3)根据题意,分点在之间或点在右侧二种情形,分别画出图形,利用平行线的性质解决问题.
【详解】(1)解:将线段平移至,
,,
,,,
令,
根据平移线段坐标关系得,
;
(2)存在.
,
设,当点在之间时,则,解得,
,,
当点在点右侧时,则,解得,
,
综上:或;
(3)点在轴的正半轴上移动(不与点,重合),
根据点位置分两种情况分析:
①当点在之间时,作,交于,如图所示:
,
,
,
,
,
②当点在右侧时,如图所示:
,
,
,
,
综上:当点在之间时,;当点在右侧时,.
【点睛】本题是几何变换综合题,主要考查了平移的性质,坐标与图形,平行线的性质,三角形外角的性质,运用分类讨论思想是解题的关键.
6.(1)A(0,6),C(8,0)
(2)存在,2.4
(3)①见解析;②∠GOD+∠ACE=∠OHC
【分析】(1)根据二次根式和绝对值的非负性即可求解;
(2)先表示出OQ,OP,利用两个三角形面积相等,建立方程求解即可得出结论;
(3)①先判断出∠OAC=∠AOD,根据OA平分∠GOD,得出∠GOA=∠AOD,进而推出∠GOA=∠OAC,即可得证;
②过点H作交x轴于F,根据平行线的性质得出,,进而得出,即可求解.
【详解】(1)∵,
∴,,∴,,
∴A(0,6),C(8,0);
(2)由(1)知,A(0,6),C(8,0),
∴OA=6,OB=8,由运动知,OQ=t,PC=2t,
∴,
∵D(4,3),
∴,
,
∵与的面积相等,
∴,
∴t=2.4,
∴存在t=2.4时,使得与的面积相等;
(3)①∵x轴轴,
∴∠AOC=∠DOC+∠AOD=90°
∴∠OAC+∠ACO=90°,
又∵∠DOC=∠DCO,
∴∠OAC=∠AOD,
∵OA平分∠GOD,
∴∠GOA=∠AOD,
∴∠GOA=∠OAC,
∴
②如图,过点H作交x轴于F,
∴
∴,
∵,
∴,
∴,
即.
【点睛】本题考查了二次根式和绝对值的非负性,三角形的面积公式,角平分线的定义,平行线的性质,正确作出辅助线是解本题的关键.
7.(1)a=2,b=3,c=4;
(2)3﹣m
(3)存在,点P(﹣3,)
【分析】(1)根据非负数的性质,即可解答;
(2)四边形ABOP的面积=△APO的面积+△AOB的面积,即可解答;
(3)存在,根据面积相等求出m的值,即可解答.
【详解】(1)由已知|a﹣2|+=0和≤0可得:
a﹣2=0,b﹣3=0,c﹣4=0,
解得:a=2,b=3,c=4;
(2)∵a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴OA=2,OB=3,
∵=×2×3=3,
=×2×(﹣m)=﹣m,
∴=+=3+(﹣m)=3﹣m
(3)存在,
∵=×4×3=6,=,
∴3﹣m=6,
解得m=﹣3,
∴存在点P(﹣3,),使=.
【点睛】本题考查了坐标与图形性质,实数的非负性,熟练掌握实数的非负性,灵活运用分割法求面积是解题的关键.
8.(1)
(2)①平移的方向为点到点的方法(或向轴负半轴方向或点到点的方向),;②存在,或
【分析】(1)先求出,进而求出,即可求出答案;
(2)直接用平移的性质,即可得出答案;
先利用面积是面积的两倍得出,再分三种情况,利用建立方程求解,即可求出答案.
【详解】(1)解:当时,,
,
,
,
.
(2)解:如图,
点的横坐标为,
,
,
,
,
,
将线段左右平移,使得点落在坐标原点,
平移的方向为点到点的方法或向轴负半轴方向或点到点的方向,
距离为,
点的坐标为;
由平移知,
,
,
面积是面积的两倍,
,
,
设点的坐标为,
当点在点上方时,,,
,
,
;
当点在线段上时,,,
,
,
;
当点在轴下方时,,,
,
,不符合题意;
即或.
【点睛】此题主要考查了平移的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.
9.(1)2,-2
(2)不改变,=45°
(3)点Q的坐标为(0,2)或(0,-6)
【分析】(1)根据“两个非负数和为0,则这两个非负数都为0”即可求解;
(2)根据平行线得性质,证明∠ADC=∠BCD+∠PAD,结合角平分线的性质,证明∠BCD+∠PAD等于一个固定值即可;
(3)易证△ABP为等腰直角三角形,从而得到AP与y轴交点坐标,将△APQ分割成两个三角形即可求解.
【详解】(1)∵,
∴a+2=0,b-2=0,
∴a=-2,b=2,
故答案为:2,-2.
(2)
连接AC,
∵,
∴∠BCA+∠PAC=180°,
∴∠BCD+∠PAD=180°-(∠1+∠2),
∵∠ADC=180°-(∠1+∠2),
∴∠ADC=∠BCD+∠PAD,
∵,
∴∠PAB=∠CBA,
∵∠CBA+∠OCB=90°,
∴∠PAB+∠OCB=90°,
∵、分别平分、,
∴∠BCD+∠PAD=(∠PAB+∠OCB)=45°,
∴∠ADC=45°,不会改变.
(3)
如图∶令AP与y轴交于点E,
∵点P的纵坐标为-4,
∴点P到x轴距离为4,即BP=4,
∵A(-2,0),B(2,0),
∴AB=4,
∴,
∵AB=BP=4,∠ABP=90°,
∴∠OAE=45°,
∵∠AOE=90°,
∴∠AEO=45°,即OA=OE=2,
设点Q的坐标为(0,m),
①当点Q在点E上方时:QE=m+2,
,
即:,解得:m=2,
∴Q(0,2),
②当点Q在点E下方时:QE=-2-m,
,
即:,解得:m=-6,
∴Q(0,-6),
综上:点Q的坐标为(0,2)或(0,-6).
【点睛】本题主要考查了平面直角坐标系中点的坐标特征,角平分线的定义,平行线的性质,熟练相关内容是解题的关键.
10.(1)见解析
(2)见解析;点B1(0,﹣4),C1的坐标(2,﹣2)
(3)存在,M(0,4)或(0,-2)
【分析】(1)根据A、B、C的坐标画出图形即可;
(2)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可;
(3)设M(0,m),构建方程求解即可.
【详解】(1)解:如图,△ABC即为所求;
(2)如图,△A1B1C1即为所求,
点B1(0,﹣4),C1的坐标(2,﹣2);
(3)设M(0,m),由题意,,
解得m=-2或4,
∴M(0,4)或(0,-2).
【点睛】本题主要考查了坐标与图形、平移变换以及三角形面积等知识,解题关键是掌握平移变换的性质以及利用参数构建方程解决问题.
11.(1),
(2)
(3)的值为或
【分析】(1)利用非负数的性质,求出,的值,再利用平移变换的性质求解;
(2)根据,求解即可;
(3)分两种情形:当点在上时,当点在上时,分别求解即可.
【详解】(1)解:,
又,,
,,
,,
线段是由线段向右平移个单位得到,
,,
故答案为:,;
(2)解:如图,连接.
当时,,
;
(3)解:,
当四边形的面积时,点在线段或线段上,
当点在上时,,
解得.
当点在上时,,
解得,
综上所述,满足条件的的值为或.
【点睛】本题属于四边形综合题,考查了四边形的面积,平移变换,非负数的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
12.(1)△ABC的面积=4;
(2)∠AED=45°;
(3)P点的坐标为(0,3)或(0,-1).
【分析】(1)根据算术平方根和偶次方的非负性,求出a,b的值即可解决问题;
(2)如图2,过E作EF∥AC,利用平行线的性质以及角平分线的定义解决问题即可;
(3)分两种情形:①当P在y轴正半轴上时,如图3-1中.②当P在y轴负半轴上时,如图3-2,分别求解即可.
【详解】(1)解:∵+(b-2)2=0,
∴a+2=0,b-2=0,
∴a=-2,b=2,
∴A(-2,0),C(2,2),
∵CB⊥AB,
∴B(2,0),
∴AB=4,CB=2,
∴△ABC的面积=×4×2=4;
(2)解:如图2,过E作EF∥AC,
∵CB⊥x轴,
∴轴,∠CBA=90°,
∴∠ODB=∠6,
又∵BD∥AC,
∴∠CAB=∠5,
∴∠CAB+∠ODB=∠5+∠6=180°-∠CBA=90°,
∵BD∥AC,
∴BD∥AC∥EF,
∴∠1=∠3,∠2=∠4,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠CAB,∠4=∠ODB,
∴∠AED=∠1+∠2=∠3+∠4=(∠CAB+∠ODB)=45°;
(3)解:①当P在y轴正半轴上时,如图3-1中,
设点P(0,t),分别过点P,A作轴,轴,MN交BC的延长线于点M,AN交MN于点N,则四边形ABMN是矩形,
则AN=t,CM=t-2,MN=AB=4,PM=PN=2,
∵,
∴,
∴×4(t-2+t)-×2×t-×2(t-2)=4,
解得t=3,
即点P的坐标为(0,3);
②当P在y轴负半轴上时,如图3-2,同①作辅助线,
设点P(0,a),则AN=-a,CM=-a+2,PM=PN=2,
∵,
∴×4×(-a+2-a)-×2 (-a)-×2(2-a)=4,
解得a=-1,
∴点P的坐标为(0,-1).
综上所述,P点的坐标为(0,3)或(0,-1).
【点睛】本题属于三角形综合题,考查了非负数的性质、三角形的面积公式,平行线的性质,依据三角形的面积公式、梯形的面积公式依据图形中相关图形之间的面积关系列出关于a和t的方程是解题的关键.
13.(1)的面积为12
(2)存在点,使,其点坐标为或或
【分析】(1)根据非负数的性质求得a、b的值,进而根据三角形的面积公式求得结果;
(2)分两种情况:点P在x轴上,点P在y轴上,分别根据三角形的面积关系列出方程求解便可.
【详解】(1),
,,
,,
,,
的面积为:;
(2)当点在轴上时,如图,
设的坐标为,则
,
或舍去,
;
当点在轴上时,如图,
设的坐标为,则
,
,
或,
综上,存在点,使,其点坐标为或或.
【点睛】本题主要考查了直角坐标系中点的特征,非负数的性质,三角形的面积,关键是数形结合运用点的坐标进行求得三角形的高与底边长.
14.(1),
(2),,
(3)
【分析】(1)根据平方和绝对值的非负性求解.
(2)①设出点M的坐标,利用M的坐标表示出长度后借助面积公式和面积关系求解;
②在坐标轴的不同位置设出不同的M的坐标,再根据题中面积关系分类讨论求解.
(3)根据平行线、角平分线的性质得出、的关系,再得出的值为定值,从而求得其值.
【详解】(1)∵,,,
∴,,
解得,.
(2)①设,
由题意可得:
,,
中OM边上的高为1,中AB边上的高为2,
∵,
∴,
解得,
②由(1)得,
当M在y轴负半轴上时,有,
解得,
当M在x轴上时,设,
则,中OM边上的高为2,
则,
解得,
,,
(3)
如图所示,
由题意可得:
平分,
,
轴
,
【点睛】本题考查利用坐标计算长度,三角形面积的计算,角平分线、平行线的性质及分类讨论的思想,解决本题的关键是熟悉各性质并综合应用.
15.(1)a=-1,b=4,点A(-1,0),点B(4,0),点D(0,3),点C(5,3);
(2)△ABP的面积不变,△ABP的面积为
(3)存在,点M(-1,0)或(9,0).
【分析】(1)由非负性可求a,b的值,即可求点A,点B坐标,由平移的性质可求点C,点D坐标;
(2)由平移的性质可得ABCD,由三角形面积公式可求解;
(3)由三角形的面积公式可求BM=5,即可求解.
【详解】(1)解:∵
∴4-b≥0,b-4≥0,
∴b=4,
∴a=-1,
∴点A(-1,0),点B(4,0),
∵将点A,B分别向上平移3个单位长度,再向右平移1个单位长度,得到点A,B的对应点D,C,
∴点D(0,3),点C(5,3);
(2)△ABP的面积不变,理由如下:
由平移可得ABCD,
∴点P到AB的距离为OD的长,
∵点A(-1,0),点B(4,0),点D(0,3),点C(5,3),
∴AB=CD=5,OD=3,
∴△ABP的面积=
(3)如图,连接AC,BD,
∵△MBD的面积与△ACD的面积相等,
∴×CD×OD=×BM×OD,
∴BM=5,
∵点B(4,0),
∴点M(-1,0)或(9,0)
【点睛】本题考查了非负数的性质,坐标与图形,平移的性质,综合运用以上知识是解题的关键.
16.(1)
(2)
(3)存在点,使得四边形的面积与的面积相等
【分析】(1)根据非负数的性质进行求解即可;
(2)根据进行求解即可;
(3)先求出,进而得到关于m的方程,解方程即可得到答案.
【详解】(1)解;∵,,,,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∵,,
∴;
(3)解;∵,
∴轴,
∴,
∵四边形的面积与的面积相等,
∴,
∴,
∴,
∴存在点,使得四边形的面积与的面积相等.
【点睛】本题考查了坐标与图形性质,非负数的性质,熟练掌握非负数的性质,灵活运用分割法求面积是解题的关键.
17.(1)12;
(2)或;
(3)或.
【分析】(1)根据平移的性质求出点,的坐标,根据平行四边形的面积公式求出四边形的面积;
(2)根据三角形的面积公式计算即可;
(3)根据直线上点的坐标特征设出点的坐标,根据三角形的面积公式计算即可.
【详解】(1)解:(1)∵点,的坐标分别为,,线段先向上平移3个单位,再向右平移1个单位,得到线段,
∴点的坐标为,点的坐标为,,
∴四边形的面积;
(2)存在,
设点的坐标为,
由题意得:,
解得:,
∴点的坐标为或;
(3)设点的坐标为,
则,
由题意得:,
解得:或,
则点的坐标为或.
【点睛】本题考查的是平移的性质、三角形的面积计算、点的坐标特征,根据平移变换的性质求出点,的坐标是解题的关键.
18.(1),3
(2),2,
(3)或
【分析】(1)可将变形为,再根据平方和绝对值的非负性即可求出a和b的值;
(2)由M点坐标即可直接得出点M到x轴距离为,到y轴距离为.又可求出,即可利用三角形面积公式求出;
(3)将代入,得.设,则.即得出,解出t的值,即得出点P的坐标.
【详解】(1)∵,
∴,
∴,解得:.
故答案为:,3;
(2)∵,
∴点M到x轴距离为,到y轴距离为.
由(1)可知,,
∴,
∴.
故答案为:,2,;
(3)当时,.
设,
∴.
∵,
∴,
解得:,
∴或.
【点睛】本题考查非负数的性质,点到坐标轴的距离,坐标与图形.利用数形结合的思想是解题关键.
19.(1)36
(2)或
【分析】(1)先根据非负数的性质求出,的值,进而得出,两点的坐标,根据三角形的面积公式即可得出结论;
(2)设,利用三角形和三角形的面积相等可得到关于的方程,再解方程求出即可得点坐标.
【详解】(1),
,,
解得,,
,,
轴,
,
,,
;
(2)设,
,
,
三角形和三角形的面积相等,,
,
,即,
解得:或,
或;
【点睛】本题昰三角形综合题,考查了非负数的性质、坐标与图形性质以及三角形面积公式,理解坐标与长度的关系是解题的关键.
20.(1);
(2),;
(3)存在点P,其坐标为或.
【分析】(1)利用平移的性质确定出平移的方向和距离,进而可得点D的坐标;
(2)设D点纵坐标为y,由平移的性质可得,,然后根据建立方程求出y的值即可;
(3)设出点P的坐标,表示出,然后根据建立方程求解即可.
【详解】(1)解:∵平移后的对应点为,
∴点B向左平移了5个单位长度,向上平移了4个单位长度,
∴A点平移后的对应点;
(2)解:设D点纵坐标为y,
∵点C在y轴上,点D在第二象限,
∴线段向左平移3个单位长度,向上平移个单位长度,
∴,,
连接,
则,
即
解得:,
∴,;
(3)解:设点,
∴,
∵,
∴,
∴,
∴或,
∴存在点P,其坐标为或.
【点睛】此题是几何变换综合题,主要考查了平移的性质,坐标与图形性质,解本题的关键是平移性质的灵活运用,用面积关系建立方程.
21.(1)或
(2)-2m
(3)或
【分析】(1)根据到两坐标轴的距离相等,构建方程,求出m,再由,且,求出N的坐标即可;
(2)根据三角形面积公式求出即可;
(3)P点在y轴上,根据面积公式构建方程,即可解决问题.
【详解】(1)解:∵到坐标轴的距离相等,
∴,或8,
∵M为第三象限内一点,
∴,
∴,
∵,且,
∵,且,
∴或.
故答案为:或;
(2)∵M为,且M在第三象限,
∴,
∴的面积;
(3)当时,的面积为,
∵的面积是的面积的2倍,
∴,
∴,,
∴或.
【点睛】本题属于三角形综合题,考查了三角形的面积、坐标与图形的性质等知识点,难度适中,能准确求三角形的面积和掌握图形与坐标的性质是关键.
22.(1)8;
(2)存在,点的坐标为或;
(3)当点在线段的延长线上运动时,; 当点在线段的延长线上运动时,;当点在线段上运动时,.
【分析】(1)根据点的平移规律可得,的坐标,然后利用即可求出四边形的面积;
(2)根据的面积是面积的2倍,得,即可求出点的坐标;
(3)当点在线段延长线上运动时,作,当点在线段的延长线上时,作,当点在线段上运动时,作,分别根据平行线的性质和平行线间的传递性求解即可.
【详解】(1)解:∵点,的坐标分别为、,
∴将点,分别向上平移2个单位长度,再向右平移1个单位长度,得到,的对应点,,
∴,,,,,
∴四边形的面积为:
.
∴点的坐标为,点的坐标为,四边形的面积为.
(2)存在,
如图,设,
∵,,
∴,
又∵的面积是面积的2倍.
∴,
∴,
∵,
∴,
解得:或,
∴点的坐标为或.
(3)当点在线段延长线上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
当点在线段的延长线上时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
当点在线段上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
综上所述:当点在线段的延长线上运动时,;
当点在线段的延长线上运动时,;
当点在线段上运动时,.
【点睛】本题考查平行线的判定和性质,点平移的规律,梯形的面积,三角形的面积等知识点.对点的位置进行分类讨论是解题的关键.
23.(1)44
(2)能,点P坐标为
【分析】(1)利用分割法,把四边形分割成一个三角形加上一个梯形后再减去一个三角形求面积;
(2)分两种情况:点P在x轴上,点P在y轴上,利用割补法求三角形的面积,进行求解即可.
【详解】(1)解:(1)如图,
过D,C分别作垂直于,E、F分别为垂足,则有:
,
;
故四边形ABCD的面积为44.
(2)当点P在x轴上,设P点坐标为;如图:
,
解得:或27,
点P坐标为;
当点P在y轴上,设P点坐标为(0,y),延长交轴于点,过点作轴于,设,
则:,
即:,
解得:,
∴
①P在直线上方时,
,解得:;
点P坐标为;
②P在直线下方时,
,
解得,
∴点P坐标.
综上:点P坐标为.
【点睛】本题考查坐标与图形,熟练掌握割补法求图形的面积是解题的关键.
答案第1页,共2页
答案第1页,共2页
存在性问题涉及的知识面广,综合性强,充满生机,要求同学们有扎实的基础知识和熟练的基本技能,因此存在性问题已成为近几年中考数学命题的一个热点。
解决存在性问题一般套路:假设存在→推理论证→得岀结论。简单地说就是若能导出合理的结果,就做出“存在”的判断,导出矛盾,就做出不存在的判断。
具体来说,我们可以归纳出三种解决存在性问题的解题策略:
1、直接求解法
直接从已知条件入手,逐步试探求出满足条件的对象,使问题得到解决。
2、假设求解法
先假设结论存在,再从已知条件和定义定理公理出发进行演绎推理若得到和题意相容的结论,则假设成立结论也存在;否则假设不成立结论不存在。
3、反证法
反证法是证明否定型存在性问题的主要方,特别是在无限个候选对象中证明某种数学对象不存在时,逐一淘汰的方法几乎不能实行,更需要使用反证法。
一、解答题
1.如图所示的正方形网格中,每个小正方形的边长为1个单位,格点三角形ABC.
(1)将△ABC平移至,使得点的坐标为(3,0),请画出平移后的三角形,并写出点,的坐标;
(2)若ABC的边上存在一点P(a,b),则平移后得到的点的坐标为 .
2.如图所示,,,点在轴上,且.
(1)求点的坐标;
(2)求三角形的面积;
(3)在轴上是否存在点,使以、、三点为顶点的三角形的面积为?若存在,请直接写出点的坐标;若不存在,请说明理由.
3.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接AA1,AO,A1O,求△AOA1的面积.
(4)连接BA1,在y轴上是否存在点Q,使得三角形QBA1的面积为8,若存在,求出点Q的坐标;若不存在,请说明理由.
4.如图,在平面直角坐标系中,已知,,三点,其中、、满足关系式,
(1)求、、的值;
(2)如果在第二象限内有一点,请用含的式子表示四边形的面积;
(3)在(2)的条件下,是否存在点,使四边形的面积与的面积相等?若存在,求出点的坐标;若不存在,请说明理由.
5.如图,在平面直角坐标系中,已知点,点,将线段平移至,点在轴的正半轴上移动(不与点,重合),连接,,,,且.
(1)直接写出点的坐标;
(2)点在运动过程中,是否存在点,满足,如果存在,请求出点的坐标;如果不存在,请说明理由;
(3)点在运动过程中,请直接写出,,三者之间存在的数量关系.
6.如图1,以直角的直角顶点O为原点,以OC,OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0),并且满足.
(1)直接写出点A,点C的坐标;
(2)如图1,坐标轴上有两动点P,Q同时出发,点P从点C出发沿x轴负方向以每秒2个单位长度的速度匀速运动,点Q从点O出发沿y轴正方向以每秒1个单位长的速度匀速运动,当点P到达点O整个运动随之结束;点D的坐标是(4,3),设运动时间为t秒.是否存在t,使得与的面积相等?若存在,求出t的值;若不存在,说明理由;
(3)如图2,在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且OA平分∠DOG,点E是线段OA上一动点,连接CE交OD于点H,当点E在OA上运动的过程中,
①说明的理由
②直接写出∠DOG,∠OHC,∠ACE之间的数量关系.
7.如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式,.
(1)求a、b、c的值:
(2)如果在第二象限内有一点,请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
8.如图在平面直角坐标系内,、分别在轴、轴正半轴上,且,点的横坐标为;
(1)当时,求点坐标;
(2)将线段左右平移,使得点落在坐标原点,此时,点落在点的位置.
请直接写出平移的方向和距离以及点的坐标;(用含的代数式表示)
轴上是否存在点,使得面积是面积的两倍,如果存在,直接写出点的坐标(用含的代数式表示),如果不存在,请说明理由.
9.如图,在平面直角坐标系中,,,且满足,过点作直线轴,点是直线上一动点,连接,过点作交轴于点,,分别平分,.
(1)填空:_______,______;
(2)在点的运动过程中,的度数是否变化?若不变,请求出它的度数;若变化,请说明理由;
(3)若点的纵坐标为,在轴上是否存在点,使得的面积和的面积相等?若存在,求出点坐标;若不存在,请说明理由.
10.如图,网格中每个小正方形的边长均为1个单位长度,已知A(﹣2,1),B(﹣2,﹣1),C(0,1).
(1)请在图中所示的平面直角坐标系中作出△ABC;
(2)把△ABC平移到△A1B1C1,使点A的对应点为A1的坐标为(0,﹣2),请你作出△A1B1C1,(点B1,C1分别是B,C的对应点),写出点B1,C1的坐标.
(3)y轴上是否存在点M,使,若存在,求出点M的坐标,不存在请说明理由.
11.综合与探究:如图,在平面直角坐标系中,点,的坐标分别为,且、满足,将线段沿轴方向向右平移个单位后得到线段,连接.点从原点出发,以每秒个单位的速度沿匀速运动,设运动时间为秒.
(1)点的坐标为______,点的坐标为______;
(2)当时,试求四边形的面积;
(3)是否存在这样的值,使四边形的面积等于?若存在,请直接写出的值;若不存在,请说明理由.
12.如图1,在平面直角坐标系中,,且满足,过C作轴于B.
(1)求的面积;
(2)若过B作交y轴于D,且AE,DE分别平分,如图2,求的度数;
(3)在y轴上存在点P使得和的面积相等,请直接写出P点坐标.
13.如图,点在第一象限,点,点,且、满足:.
(1)求的面积;
(2)在坐标轴上是否存在一点(不和点重合),使?若存在,请直接写出所有符合题意的点的坐标,并把求其中一个点的坐标的过程写出来.
14.如图1,在平面直角坐标系中,,,,且
(1)求,的值.
(2)①在轴的正半轴上存在一点,使,求点的坐标;
②在坐标轴的其它位置是否存在点,使仍然成立,若存在,请直接写出符合条件的点的坐标.
(3)如图2,过点作轴交轴于点,点为线段延长线上一动点,连接,平分,.当点运动时,的值是否会改变?若不变,求其值;若改变,说明理由.
15.如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足,现同时将点A,B分别向上平移3个单位长度,再向右平移1个单位长度,得到点A,B的对应点D,C,连接AD,BC,CD.
(1)求a,b的值,并直接写出点A,点B,点C,点D的坐标;
(2)如图2,点P是线段DC上的一个动点,连接PA,PB,当点P在线段DC上移动时,的面积是否变化?若不变,请求出的面积;若变化,请说明理由.
(3)在x轴上是否存在一点M,使的面积与的面积相等?若存在,请直接写出点M的坐标;若不存在,试说明理由.
16.如图,在下面直角坐标系中,已知,,三点,其中、、满足关系式和.
(1)求、、的值;
(2)如果在第二象限内有一点,请用含的式子表示四边形的面积;
(3)在(2)的条件下,是否存在点,使得四边形的面积与的面积相等?若存在,求出点的坐标;若不存在,请说明理由.
17.在平面直角坐标系中,点,的坐标分别为,,现将线段先向上平移3个单位,再向右平移1个单位,得到线段,连接,.
(1)如图1,求点,的坐标及四边形的面积;
(2)如图1,在轴上是否存在点,连接,,使?若存在这样的点,求出点的坐标;若不存在,试说明理由;
(3)如图2,点为与轴交点,在直线上是否存在点,连接,使?若存在这样的点,直接写出点的坐标;若不存在,试说明理由;
18.如图,在平面直角坐标系中,已知,,其中,满足.
(1)填空:______,________;
(2)若存在一点,点M到x轴距离_______,到y轴距离_______,求的面积(用含m的式子表示);
(3)在(2)条件下,当时,在y轴上有一点P,使得的面积与的面积相等,请求出点P的坐标.
19.如图,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)若线段与轴交于点,在轴上是否存在点,使得三角形和三角形的面积相等,若存在,求出点坐标;若不存在,请说明理由;
20.在直角坐标系中,已知线段,点A的坐标为,点B的坐标为,如图1所示.
(1)平移线段到线段,使点A的对应点为D,点B的对应点为C,若点C的坐标为,求点D的坐标;
(2)平移线段到线段,使点C在y轴的正半轴上,点D在第二象限内,连接,,如图2所示.若(表示三角形的面积),求点C、D的坐标.
(3)在(2)的条件下,在y轴上是否存在一点P,使(表示三角形的面积)?若存在,求出点P的坐标;若不存在,请说明理由.
21.如图,在平面直角坐标系中,已知,点为第三象限内一点.
(1)若到两坐标轴的距离相等,,且,则点坐标为______.
(2)若为,请用含的式子表示的面积.
(3)在(2)条件下,当时,在轴上有点,使得的面积是的面积的2倍,请直接写出点的坐标.
22.如图1 ,在平面直角坐标系中,点A、B的坐标分别为,,现同时将A、B向上平移2个单位长度,再向右平移1个单位长度,得到A、B的对应点C、D,连接、、.
(1)写出C、D的坐标并求出四边形的面积.
(2)在x 轴上 是否存在一点F,使得三角形的面积是三角形面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图 2、3、4,点 P 是直线上的一个动点,连接、,当点P在直线上运动时,请直接写出与、的数量关系.
23.如图,在平面直角坐标系中,四边形各顶点的坐标分别为
(1)求此四边形的面积.
(2)在坐标轴上,你能否找到一点P,使?若能,求出P点坐标;若不能,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)图见解析,(-1,6),(-4,3)
(2)(a-2,b+2)
【分析】(1)先由点的坐标为(3,0)判断出平移的方式,然后画出图形,再写出,的坐标;
(2)根据(1)中平移的方式解答即可.
【详解】(1)解:∵C(5,-2),(3,0),
∴三角形先向左平移了2个单位,又向上平移了2个单位,
如图,即为所求,
(-1,6),(-4,3).
(2)解:∵三角形先向左平移了2个单位,又向上平移了2个单位,
则三角形边上的点P(a,b)平移后得到点(a-2,b+2).
故答案为:(a-2,b+2).
【点睛】本题考查了坐标与图形变换-平移,判断平移的方式以及根据平移的方式确定点的坐标,由点C平移后的坐标判断平移的方式是解答本题的关键.
2.(1)或;
(2);
(3)存在,或
【分析】(1)分点在点的左边和右边两种情况解答;
(2)利用三角形的面积公式列式计算即可得解;
(3)利用三角形的面积公式列式求出点到轴的距离,然后分两种情况写出点的坐标即可.
【详解】(1)如图,
当点在点的右边时,,
当点在点的左边时,,
所以的坐标为或;
(2)的面积,
答:的面积为;
(3)设点到轴的距离为,
则,
解得,
当点在轴正半轴时,,
当点在轴负半轴时,,
综上所述,点的坐标为或
【点睛】本题考查了点的坐标的确定,三角形的面积公式,分类讨论,坐标轴上两点间的距离公式等有关知识;能求出符合条件的点的坐标是解此题的关键.
3.(1)(3,1),(1,﹣1),(4,﹣2);
(2)图形见解析;
(3)6
(4)Q点的坐标为(0,﹣1)或(0,3).
【分析】(1)利用P点和的坐标特征得到平移的方向与距离,然后利用此平移规律写出点,,的坐标;
(2)利用点,,的坐标描点即可;
(3)用一个矩形的面积分别减去三个直角三角形的面积,即可计算的面积;
(4)设Q(0,t),利用三角形面积公式得到×8×|t﹣1|=8,然后解方程求出t得到Q点的坐标.
【详解】(1)由P点和的坐标特征可得:平移是向右平移6个单位长度,再向下平移2个单位长度,此平移,点A平移后的坐标为(3,1),点B平移后的坐标为(1,﹣1),点C平移后的坐标为(4,﹣2);
故(3,1),(1,﹣1),(4,﹣2);
(2)如图,为所作;
(3)的面积=6×3﹣×3×3﹣×3×1﹣×6×2
=
=18﹣12
=6;
(4)设Q(0,t),
∵B(﹣5,1),(3,1),
∴B=3﹣(﹣5)=8,
∵的面积为8,
∴×8×|t﹣1|=8,解得t=﹣1或t=3,
∴Q点的坐标为(0,﹣1)或(0,3).
【点睛】本题考查了作图﹣平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形;解答本题关键是确定平移.
4.(1),,
(2)
(3)存在,
【分析】(1)根据几个非负数和的性质得到,分别解一元一次方程得到;
(2)根据三角形的面积公式和四边形的面积= 进行计算;
(3)可求,是已知量,根据题意,列出方程求解即可.
【详解】(1)由已知,
可得:
∴,,;
(2)由(1)知,a=2,b=3,
∴A(0,2),B(3,0),
∴OA=2,OB=3,
,,
(3)由(1)知,a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴BC=4,
∴,
∵四边形ABOP的面积与△ABC的面积相等,
∴S=6,
由(2)知,S=m+3,
∴m+3=6,
∴m=3,
∴
【点睛】本题考查了坐标与图形性质:利用坐标计算线段的长度和判断线段与坐标轴的位置关系.也考查了三角形的面积公式.
5.(1)
(2)或
(3)当点在之间时,;当点在右侧时,
【分析】(1)根据平移的性质得,,即可得出点的坐标;
(2)根据,由点的位置进行分类讨论即可得出答案;
(3)根据题意,分点在之间或点在右侧二种情形,分别画出图形,利用平行线的性质解决问题.
【详解】(1)解:将线段平移至,
,,
,,,
令,
根据平移线段坐标关系得,
;
(2)存在.
,
设,当点在之间时,则,解得,
,,
当点在点右侧时,则,解得,
,
综上:或;
(3)点在轴的正半轴上移动(不与点,重合),
根据点位置分两种情况分析:
①当点在之间时,作,交于,如图所示:
,
,
,
,
,
②当点在右侧时,如图所示:
,
,
,
,
综上:当点在之间时,;当点在右侧时,.
【点睛】本题是几何变换综合题,主要考查了平移的性质,坐标与图形,平行线的性质,三角形外角的性质,运用分类讨论思想是解题的关键.
6.(1)A(0,6),C(8,0)
(2)存在,2.4
(3)①见解析;②∠GOD+∠ACE=∠OHC
【分析】(1)根据二次根式和绝对值的非负性即可求解;
(2)先表示出OQ,OP,利用两个三角形面积相等,建立方程求解即可得出结论;
(3)①先判断出∠OAC=∠AOD,根据OA平分∠GOD,得出∠GOA=∠AOD,进而推出∠GOA=∠OAC,即可得证;
②过点H作交x轴于F,根据平行线的性质得出,,进而得出,即可求解.
【详解】(1)∵,
∴,,∴,,
∴A(0,6),C(8,0);
(2)由(1)知,A(0,6),C(8,0),
∴OA=6,OB=8,由运动知,OQ=t,PC=2t,
∴,
∵D(4,3),
∴,
,
∵与的面积相等,
∴,
∴t=2.4,
∴存在t=2.4时,使得与的面积相等;
(3)①∵x轴轴,
∴∠AOC=∠DOC+∠AOD=90°
∴∠OAC+∠ACO=90°,
又∵∠DOC=∠DCO,
∴∠OAC=∠AOD,
∵OA平分∠GOD,
∴∠GOA=∠AOD,
∴∠GOA=∠OAC,
∴
②如图,过点H作交x轴于F,
∴
∴,
∵,
∴,
∴,
即.
【点睛】本题考查了二次根式和绝对值的非负性,三角形的面积公式,角平分线的定义,平行线的性质,正确作出辅助线是解本题的关键.
7.(1)a=2,b=3,c=4;
(2)3﹣m
(3)存在,点P(﹣3,)
【分析】(1)根据非负数的性质,即可解答;
(2)四边形ABOP的面积=△APO的面积+△AOB的面积,即可解答;
(3)存在,根据面积相等求出m的值,即可解答.
【详解】(1)由已知|a﹣2|+=0和≤0可得:
a﹣2=0,b﹣3=0,c﹣4=0,
解得:a=2,b=3,c=4;
(2)∵a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴OA=2,OB=3,
∵=×2×3=3,
=×2×(﹣m)=﹣m,
∴=+=3+(﹣m)=3﹣m
(3)存在,
∵=×4×3=6,=,
∴3﹣m=6,
解得m=﹣3,
∴存在点P(﹣3,),使=.
【点睛】本题考查了坐标与图形性质,实数的非负性,熟练掌握实数的非负性,灵活运用分割法求面积是解题的关键.
8.(1)
(2)①平移的方向为点到点的方法(或向轴负半轴方向或点到点的方向),;②存在,或
【分析】(1)先求出,进而求出,即可求出答案;
(2)直接用平移的性质,即可得出答案;
先利用面积是面积的两倍得出,再分三种情况,利用建立方程求解,即可求出答案.
【详解】(1)解:当时,,
,
,
,
.
(2)解:如图,
点的横坐标为,
,
,
,
,
,
将线段左右平移,使得点落在坐标原点,
平移的方向为点到点的方法或向轴负半轴方向或点到点的方向,
距离为,
点的坐标为;
由平移知,
,
,
面积是面积的两倍,
,
,
设点的坐标为,
当点在点上方时,,,
,
,
;
当点在线段上时,,,
,
,
;
当点在轴下方时,,,
,
,不符合题意;
即或.
【点睛】此题主要考查了平移的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.
9.(1)2,-2
(2)不改变,=45°
(3)点Q的坐标为(0,2)或(0,-6)
【分析】(1)根据“两个非负数和为0,则这两个非负数都为0”即可求解;
(2)根据平行线得性质,证明∠ADC=∠BCD+∠PAD,结合角平分线的性质,证明∠BCD+∠PAD等于一个固定值即可;
(3)易证△ABP为等腰直角三角形,从而得到AP与y轴交点坐标,将△APQ分割成两个三角形即可求解.
【详解】(1)∵,
∴a+2=0,b-2=0,
∴a=-2,b=2,
故答案为:2,-2.
(2)
连接AC,
∵,
∴∠BCA+∠PAC=180°,
∴∠BCD+∠PAD=180°-(∠1+∠2),
∵∠ADC=180°-(∠1+∠2),
∴∠ADC=∠BCD+∠PAD,
∵,
∴∠PAB=∠CBA,
∵∠CBA+∠OCB=90°,
∴∠PAB+∠OCB=90°,
∵、分别平分、,
∴∠BCD+∠PAD=(∠PAB+∠OCB)=45°,
∴∠ADC=45°,不会改变.
(3)
如图∶令AP与y轴交于点E,
∵点P的纵坐标为-4,
∴点P到x轴距离为4,即BP=4,
∵A(-2,0),B(2,0),
∴AB=4,
∴,
∵AB=BP=4,∠ABP=90°,
∴∠OAE=45°,
∵∠AOE=90°,
∴∠AEO=45°,即OA=OE=2,
设点Q的坐标为(0,m),
①当点Q在点E上方时:QE=m+2,
,
即:,解得:m=2,
∴Q(0,2),
②当点Q在点E下方时:QE=-2-m,
,
即:,解得:m=-6,
∴Q(0,-6),
综上:点Q的坐标为(0,2)或(0,-6).
【点睛】本题主要考查了平面直角坐标系中点的坐标特征,角平分线的定义,平行线的性质,熟练相关内容是解题的关键.
10.(1)见解析
(2)见解析;点B1(0,﹣4),C1的坐标(2,﹣2)
(3)存在,M(0,4)或(0,-2)
【分析】(1)根据A、B、C的坐标画出图形即可;
(2)利用平移变换的性质分别作出A,B,C的对应点A1,B1,C1即可;
(3)设M(0,m),构建方程求解即可.
【详解】(1)解:如图,△ABC即为所求;
(2)如图,△A1B1C1即为所求,
点B1(0,﹣4),C1的坐标(2,﹣2);
(3)设M(0,m),由题意,,
解得m=-2或4,
∴M(0,4)或(0,-2).
【点睛】本题主要考查了坐标与图形、平移变换以及三角形面积等知识,解题关键是掌握平移变换的性质以及利用参数构建方程解决问题.
11.(1),
(2)
(3)的值为或
【分析】(1)利用非负数的性质,求出,的值,再利用平移变换的性质求解;
(2)根据,求解即可;
(3)分两种情形:当点在上时,当点在上时,分别求解即可.
【详解】(1)解:,
又,,
,,
,,
线段是由线段向右平移个单位得到,
,,
故答案为:,;
(2)解:如图,连接.
当时,,
;
(3)解:,
当四边形的面积时,点在线段或线段上,
当点在上时,,
解得.
当点在上时,,
解得,
综上所述,满足条件的的值为或.
【点睛】本题属于四边形综合题,考查了四边形的面积,平移变换,非负数的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
12.(1)△ABC的面积=4;
(2)∠AED=45°;
(3)P点的坐标为(0,3)或(0,-1).
【分析】(1)根据算术平方根和偶次方的非负性,求出a,b的值即可解决问题;
(2)如图2,过E作EF∥AC,利用平行线的性质以及角平分线的定义解决问题即可;
(3)分两种情形:①当P在y轴正半轴上时,如图3-1中.②当P在y轴负半轴上时,如图3-2,分别求解即可.
【详解】(1)解:∵+(b-2)2=0,
∴a+2=0,b-2=0,
∴a=-2,b=2,
∴A(-2,0),C(2,2),
∵CB⊥AB,
∴B(2,0),
∴AB=4,CB=2,
∴△ABC的面积=×4×2=4;
(2)解:如图2,过E作EF∥AC,
∵CB⊥x轴,
∴轴,∠CBA=90°,
∴∠ODB=∠6,
又∵BD∥AC,
∴∠CAB=∠5,
∴∠CAB+∠ODB=∠5+∠6=180°-∠CBA=90°,
∵BD∥AC,
∴BD∥AC∥EF,
∴∠1=∠3,∠2=∠4,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠CAB,∠4=∠ODB,
∴∠AED=∠1+∠2=∠3+∠4=(∠CAB+∠ODB)=45°;
(3)解:①当P在y轴正半轴上时,如图3-1中,
设点P(0,t),分别过点P,A作轴,轴,MN交BC的延长线于点M,AN交MN于点N,则四边形ABMN是矩形,
则AN=t,CM=t-2,MN=AB=4,PM=PN=2,
∵,
∴,
∴×4(t-2+t)-×2×t-×2(t-2)=4,
解得t=3,
即点P的坐标为(0,3);
②当P在y轴负半轴上时,如图3-2,同①作辅助线,
设点P(0,a),则AN=-a,CM=-a+2,PM=PN=2,
∵,
∴×4×(-a+2-a)-×2 (-a)-×2(2-a)=4,
解得a=-1,
∴点P的坐标为(0,-1).
综上所述,P点的坐标为(0,3)或(0,-1).
【点睛】本题属于三角形综合题,考查了非负数的性质、三角形的面积公式,平行线的性质,依据三角形的面积公式、梯形的面积公式依据图形中相关图形之间的面积关系列出关于a和t的方程是解题的关键.
13.(1)的面积为12
(2)存在点,使,其点坐标为或或
【分析】(1)根据非负数的性质求得a、b的值,进而根据三角形的面积公式求得结果;
(2)分两种情况:点P在x轴上,点P在y轴上,分别根据三角形的面积关系列出方程求解便可.
【详解】(1),
,,
,,
,,
的面积为:;
(2)当点在轴上时,如图,
设的坐标为,则
,
或舍去,
;
当点在轴上时,如图,
设的坐标为,则
,
,
或,
综上,存在点,使,其点坐标为或或.
【点睛】本题主要考查了直角坐标系中点的特征,非负数的性质,三角形的面积,关键是数形结合运用点的坐标进行求得三角形的高与底边长.
14.(1),
(2),,
(3)
【分析】(1)根据平方和绝对值的非负性求解.
(2)①设出点M的坐标,利用M的坐标表示出长度后借助面积公式和面积关系求解;
②在坐标轴的不同位置设出不同的M的坐标,再根据题中面积关系分类讨论求解.
(3)根据平行线、角平分线的性质得出、的关系,再得出的值为定值,从而求得其值.
【详解】(1)∵,,,
∴,,
解得,.
(2)①设,
由题意可得:
,,
中OM边上的高为1,中AB边上的高为2,
∵,
∴,
解得,
②由(1)得,
当M在y轴负半轴上时,有,
解得,
当M在x轴上时,设,
则,中OM边上的高为2,
则,
解得,
,,
(3)
如图所示,
由题意可得:
平分,
,
轴
,
【点睛】本题考查利用坐标计算长度,三角形面积的计算,角平分线、平行线的性质及分类讨论的思想,解决本题的关键是熟悉各性质并综合应用.
15.(1)a=-1,b=4,点A(-1,0),点B(4,0),点D(0,3),点C(5,3);
(2)△ABP的面积不变,△ABP的面积为
(3)存在,点M(-1,0)或(9,0).
【分析】(1)由非负性可求a,b的值,即可求点A,点B坐标,由平移的性质可求点C,点D坐标;
(2)由平移的性质可得ABCD,由三角形面积公式可求解;
(3)由三角形的面积公式可求BM=5,即可求解.
【详解】(1)解:∵
∴4-b≥0,b-4≥0,
∴b=4,
∴a=-1,
∴点A(-1,0),点B(4,0),
∵将点A,B分别向上平移3个单位长度,再向右平移1个单位长度,得到点A,B的对应点D,C,
∴点D(0,3),点C(5,3);
(2)△ABP的面积不变,理由如下:
由平移可得ABCD,
∴点P到AB的距离为OD的长,
∵点A(-1,0),点B(4,0),点D(0,3),点C(5,3),
∴AB=CD=5,OD=3,
∴△ABP的面积=
(3)如图,连接AC,BD,
∵△MBD的面积与△ACD的面积相等,
∴×CD×OD=×BM×OD,
∴BM=5,
∵点B(4,0),
∴点M(-1,0)或(9,0)
【点睛】本题考查了非负数的性质,坐标与图形,平移的性质,综合运用以上知识是解题的关键.
16.(1)
(2)
(3)存在点,使得四边形的面积与的面积相等
【分析】(1)根据非负数的性质进行求解即可;
(2)根据进行求解即可;
(3)先求出,进而得到关于m的方程,解方程即可得到答案.
【详解】(1)解;∵,,,,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∵,,
∴;
(3)解;∵,
∴轴,
∴,
∵四边形的面积与的面积相等,
∴,
∴,
∴,
∴存在点,使得四边形的面积与的面积相等.
【点睛】本题考查了坐标与图形性质,非负数的性质,熟练掌握非负数的性质,灵活运用分割法求面积是解题的关键.
17.(1)12;
(2)或;
(3)或.
【分析】(1)根据平移的性质求出点,的坐标,根据平行四边形的面积公式求出四边形的面积;
(2)根据三角形的面积公式计算即可;
(3)根据直线上点的坐标特征设出点的坐标,根据三角形的面积公式计算即可.
【详解】(1)解:(1)∵点,的坐标分别为,,线段先向上平移3个单位,再向右平移1个单位,得到线段,
∴点的坐标为,点的坐标为,,
∴四边形的面积;
(2)存在,
设点的坐标为,
由题意得:,
解得:,
∴点的坐标为或;
(3)设点的坐标为,
则,
由题意得:,
解得:或,
则点的坐标为或.
【点睛】本题考查的是平移的性质、三角形的面积计算、点的坐标特征,根据平移变换的性质求出点,的坐标是解题的关键.
18.(1),3
(2),2,
(3)或
【分析】(1)可将变形为,再根据平方和绝对值的非负性即可求出a和b的值;
(2)由M点坐标即可直接得出点M到x轴距离为,到y轴距离为.又可求出,即可利用三角形面积公式求出;
(3)将代入,得.设,则.即得出,解出t的值,即得出点P的坐标.
【详解】(1)∵,
∴,
∴,解得:.
故答案为:,3;
(2)∵,
∴点M到x轴距离为,到y轴距离为.
由(1)可知,,
∴,
∴.
故答案为:,2,;
(3)当时,.
设,
∴.
∵,
∴,
解得:,
∴或.
【点睛】本题考查非负数的性质,点到坐标轴的距离,坐标与图形.利用数形结合的思想是解题关键.
19.(1)36
(2)或
【分析】(1)先根据非负数的性质求出,的值,进而得出,两点的坐标,根据三角形的面积公式即可得出结论;
(2)设,利用三角形和三角形的面积相等可得到关于的方程,再解方程求出即可得点坐标.
【详解】(1),
,,
解得,,
,,
轴,
,
,,
;
(2)设,
,
,
三角形和三角形的面积相等,,
,
,即,
解得:或,
或;
【点睛】本题昰三角形综合题,考查了非负数的性质、坐标与图形性质以及三角形面积公式,理解坐标与长度的关系是解题的关键.
20.(1);
(2),;
(3)存在点P,其坐标为或.
【分析】(1)利用平移的性质确定出平移的方向和距离,进而可得点D的坐标;
(2)设D点纵坐标为y,由平移的性质可得,,然后根据建立方程求出y的值即可;
(3)设出点P的坐标,表示出,然后根据建立方程求解即可.
【详解】(1)解:∵平移后的对应点为,
∴点B向左平移了5个单位长度,向上平移了4个单位长度,
∴A点平移后的对应点;
(2)解:设D点纵坐标为y,
∵点C在y轴上,点D在第二象限,
∴线段向左平移3个单位长度,向上平移个单位长度,
∴,,
连接,
则,
即
解得:,
∴,;
(3)解:设点,
∴,
∵,
∴,
∴,
∴或,
∴存在点P,其坐标为或.
【点睛】此题是几何变换综合题,主要考查了平移的性质,坐标与图形性质,解本题的关键是平移性质的灵活运用,用面积关系建立方程.
21.(1)或
(2)-2m
(3)或
【分析】(1)根据到两坐标轴的距离相等,构建方程,求出m,再由,且,求出N的坐标即可;
(2)根据三角形面积公式求出即可;
(3)P点在y轴上,根据面积公式构建方程,即可解决问题.
【详解】(1)解:∵到坐标轴的距离相等,
∴,或8,
∵M为第三象限内一点,
∴,
∴,
∵,且,
∵,且,
∴或.
故答案为:或;
(2)∵M为,且M在第三象限,
∴,
∴的面积;
(3)当时,的面积为,
∵的面积是的面积的2倍,
∴,
∴,,
∴或.
【点睛】本题属于三角形综合题,考查了三角形的面积、坐标与图形的性质等知识点,难度适中,能准确求三角形的面积和掌握图形与坐标的性质是关键.
22.(1)8;
(2)存在,点的坐标为或;
(3)当点在线段的延长线上运动时,; 当点在线段的延长线上运动时,;当点在线段上运动时,.
【分析】(1)根据点的平移规律可得,的坐标,然后利用即可求出四边形的面积;
(2)根据的面积是面积的2倍,得,即可求出点的坐标;
(3)当点在线段延长线上运动时,作,当点在线段的延长线上时,作,当点在线段上运动时,作,分别根据平行线的性质和平行线间的传递性求解即可.
【详解】(1)解:∵点,的坐标分别为、,
∴将点,分别向上平移2个单位长度,再向右平移1个单位长度,得到,的对应点,,
∴,,,,,
∴四边形的面积为:
.
∴点的坐标为,点的坐标为,四边形的面积为.
(2)存在,
如图,设,
∵,,
∴,
又∵的面积是面积的2倍.
∴,
∴,
∵,
∴,
解得:或,
∴点的坐标为或.
(3)当点在线段延长线上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
当点在线段的延长线上时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
当点在线段上运动时,作,如图,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
综上所述:当点在线段的延长线上运动时,;
当点在线段的延长线上运动时,;
当点在线段上运动时,.
【点睛】本题考查平行线的判定和性质,点平移的规律,梯形的面积,三角形的面积等知识点.对点的位置进行分类讨论是解题的关键.
23.(1)44
(2)能,点P坐标为
【分析】(1)利用分割法,把四边形分割成一个三角形加上一个梯形后再减去一个三角形求面积;
(2)分两种情况:点P在x轴上,点P在y轴上,利用割补法求三角形的面积,进行求解即可.
【详解】(1)解:(1)如图,
过D,C分别作垂直于,E、F分别为垂足,则有:
,
;
故四边形ABCD的面积为44.
(2)当点P在x轴上,设P点坐标为;如图:
,
解得:或27,
点P坐标为;
当点P在y轴上,设P点坐标为(0,y),延长交轴于点,过点作轴于,设,
则:,
即:,
解得:,
∴
①P在直线上方时,
,解得:;
点P坐标为;
②P在直线下方时,
,
解得,
∴点P坐标.
综上:点P坐标为.
【点睛】本题考查坐标与图形,熟练掌握割补法求图形的面积是解题的关键.
答案第1页,共2页
答案第1页,共2页
