中考名家讲座(第2讲中考数学主要知识点模块的考查)
文档属性
| 名称 | 中考名家讲座(第2讲中考数学主要知识点模块的考查) |  | |
| 格式 | zip | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-10 11:35:20 | ||
图片预览






文档简介
课件28张PPT。中考数学
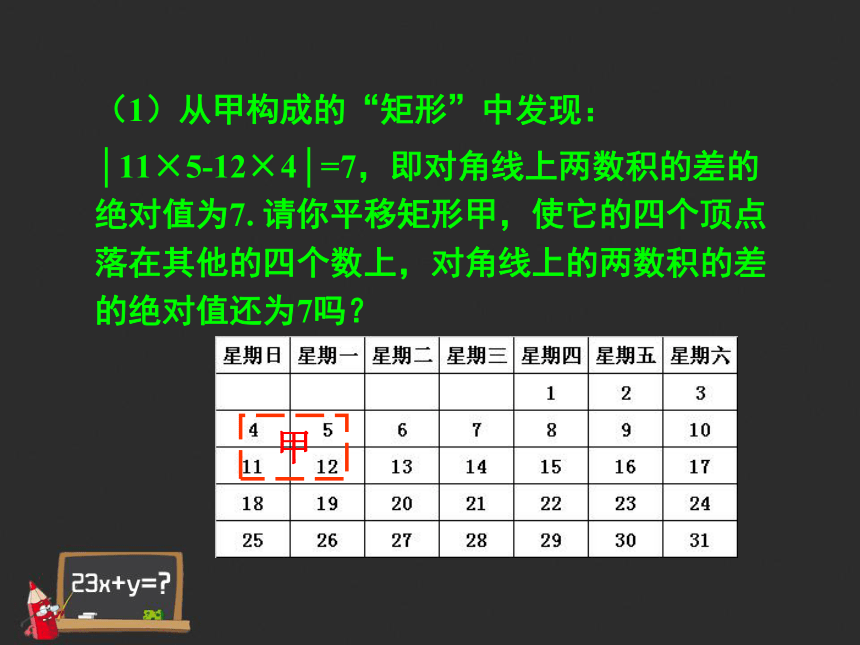
主要知识点模块的考查高级教师 李爱民主要知识点模块主要知识点模块主要知识点模块主要知识点模块整式 如图是某月的日历牌,我们在日历牌中用两种不同的方式选择四个数.(1)从甲构成的“矩形”中发现:
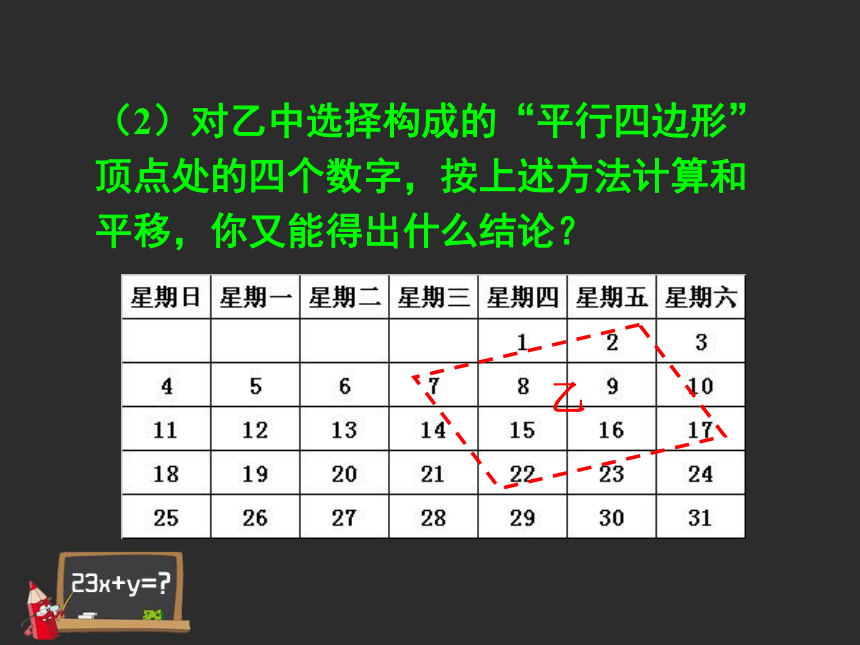
│11×5-12×4│=7,即对角线上两数积的差的绝对值为7. 请你平移矩形甲,使它的四个顶点落在其他的四个数上,对角线上的两数积的差的绝对值还为7吗?(2)对乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,你又能得出什么结论?
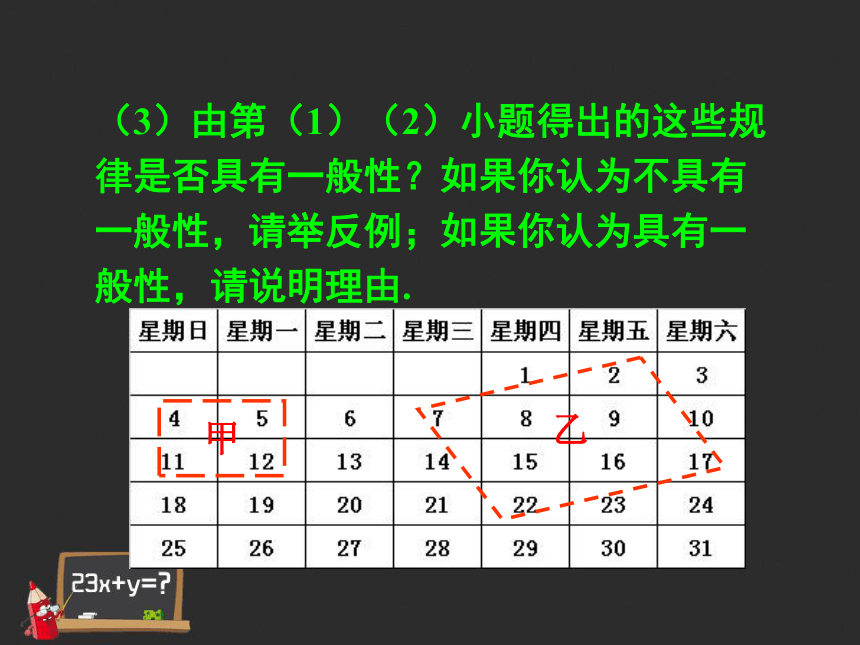
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请说明理由.
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请说明理由.
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请说明理由.
乙
方程(组) 阅读下面解方程组的方法,然后回答有关问题:
解方程组 时,如果直接消元,那将是很繁琐的,若采用下面的解法则会简便许多. 解:①-②,得 2x + 2y = 2 ,
即 x + y = 1. ③
③×16,得 16x +16y = 16. ④
②-④,得 x = -1,从而 y = 2.
∴方程组的解为
请你采用上述方法解方程组: ?
猜测方程组:
(a≠b)的解是
什么?并利用方程组的解加以验证.一元二次方程 在△ABC中,a, b, c分别为∠A, ∠B, ∠C所对的边,我们称关于x的一元二次方程ax2 +bx-c =0为“△ABC的☆方程”.
ACB根据规定解答下列问题:
(1)“△ABC的☆方程”ax2 +bx-c=0的根的情况是 (填序号);
① 有两个相等的实数根
② 有两个不相等的实数根
③ 没有实数根
(2)如图,AD为⊙O的直径, BC为弦,BC ⊥AD于E,∠DBC=30°,求“△ABC的☆方程”ax2 +bx-c=0 的解;(3)若x= c 是“△ABC的☆方程”
ax2 +bx-c=0的一个根,其中a,b,c均为整数,且ac-4b<0,求方程的另一个根.函数 (重庆)已知二次函数 y = ax2 +bx+c(a ≠ 0)的图象如图所示,对称轴为x= .下列结论中正确的是( )
A.abc>0 B.a+b=0
C.2b+c>0 D.4a+c<2b 圆 小明用一把残缺的量角器测量三角形玻璃板中∠A的大小.他将玻璃板按如图所示的方式放置在量角器上,使点A在圆弧上, AB、AC分别与圆弧交于点D、E,它们对应的刻度分别为70°、100°,则
∠A的度数为 °.阅读下面的材料:
小伟遇到这样一个问题,如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O. 若梯形ABCD的面积为1,试求以AC,BD, AD+BC 的长度为三边长的三角形的面积.平移 小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题. 他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD, AD+BC的长度为三边长的三角形,如图. 参考小伟同学思考问题的方法,解决下列问题:
如图,△ABC的三条中线分别为AD,BE,CF. (1)在下图中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC的面积为1,则以AD,BE,CF的长度为三边长的三角形的面积等于_______.谢谢!
│11×5-12×4│=7,即对角线上两数积的差的绝对值为7. 请你平移矩形甲,使它的四个顶点落在其他的四个数上,对角线上的两数积的差的绝对值还为7吗?(2)对乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,你又能得出什么结论?
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请说明理由.
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请说明理由.
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例;如果你认为具有一般性,请说明理由.
乙
方程(组) 阅读下面解方程组的方法,然后回答有关问题:
解方程组 时,如果直接消元,那将是很繁琐的,若采用下面的解法则会简便许多. 解:①-②,得 2x + 2y = 2 ,
即 x + y = 1. ③
③×16,得 16x +16y = 16. ④
②-④,得 x = -1,从而 y = 2.
∴方程组的解为
请你采用上述方法解方程组: ?
猜测方程组:
(a≠b)的解是
什么?并利用方程组的解加以验证.一元二次方程 在△ABC中,a, b, c分别为∠A, ∠B, ∠C所对的边,我们称关于x的一元二次方程ax2 +bx-c =0为“△ABC的☆方程”.
ACB根据规定解答下列问题:
(1)“△ABC的☆方程”ax2 +bx-c=0的根的情况是 (填序号);
① 有两个相等的实数根
② 有两个不相等的实数根
③ 没有实数根
(2)如图,AD为⊙O的直径, BC为弦,BC ⊥AD于E,∠DBC=30°,求“△ABC的☆方程”ax2 +bx-c=0 的解;(3)若x= c 是“△ABC的☆方程”
ax2 +bx-c=0的一个根,其中a,b,c均为整数,且ac-4b<0,求方程的另一个根.函数 (重庆)已知二次函数 y = ax2 +bx+c(a ≠ 0)的图象如图所示,对称轴为x= .下列结论中正确的是( )
A.abc>0 B.a+b=0
C.2b+c>0 D.4a+c<2b 圆 小明用一把残缺的量角器测量三角形玻璃板中∠A的大小.他将玻璃板按如图所示的方式放置在量角器上,使点A在圆弧上, AB、AC分别与圆弧交于点D、E,它们对应的刻度分别为70°、100°,则
∠A的度数为 °.阅读下面的材料:
小伟遇到这样一个问题,如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O. 若梯形ABCD的面积为1,试求以AC,BD, AD+BC 的长度为三边长的三角形的面积.平移 小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题. 他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD, AD+BC的长度为三边长的三角形,如图. 参考小伟同学思考问题的方法,解决下列问题:
如图,△ABC的三条中线分别为AD,BE,CF. (1)在下图中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC的面积为1,则以AD,BE,CF的长度为三边长的三角形的面积等于_______.谢谢!
同课章节目录
