中考名家讲座第13讲中考数学压轴题精讲

课件41张PPT。 压轴题解题策略特级教师：张文娣 【知识精讲】
几何综合题是中考试卷中常见的题型，常作为中考的压轴题。 几何综合题分类
大致可分为几何计算型综合题和几何论证型综合题，主要考查学生综合运用几何知识的能力。 几何综合题的特点
这类题往往图形较复杂，涉及知识点较多，题设和结论之间的关系较隐蔽，常常需要添加辅助线来解决。 解几何综合题需注意：
1.图形的直观提示；
2.分析挖掘题目的隐含条件、拓展条件，为解题创造条件、打好基础。【例题】阅读下列材料：
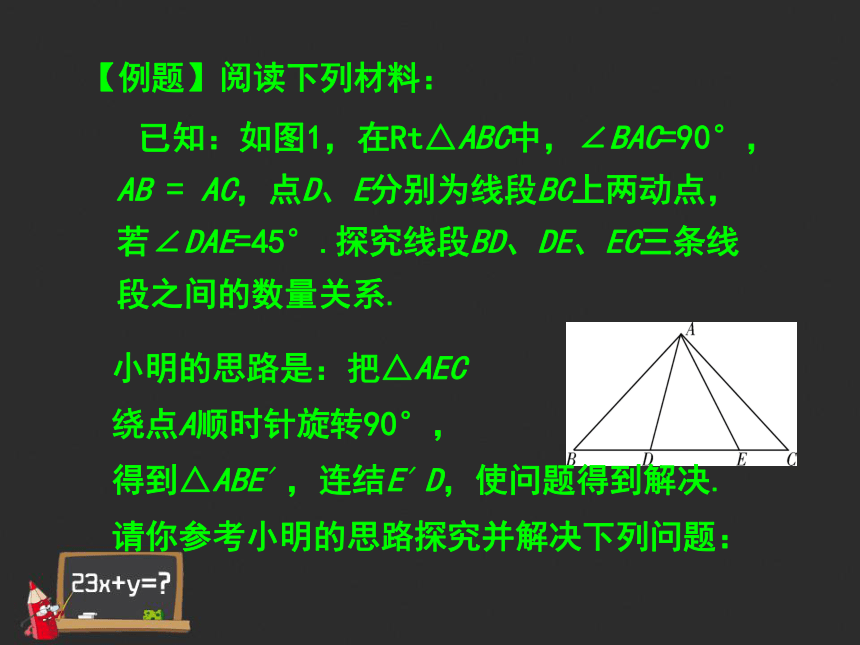
已知：如图1，在Rt△ABC中，∠BAC=90°，AB = AC，点D、E分别为线段BC上两动点，若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系. 小明的思路是：把△AEC
绕点A顺时针旋转90°，
得到△ABE′，连结E′D，使问题得到解决.
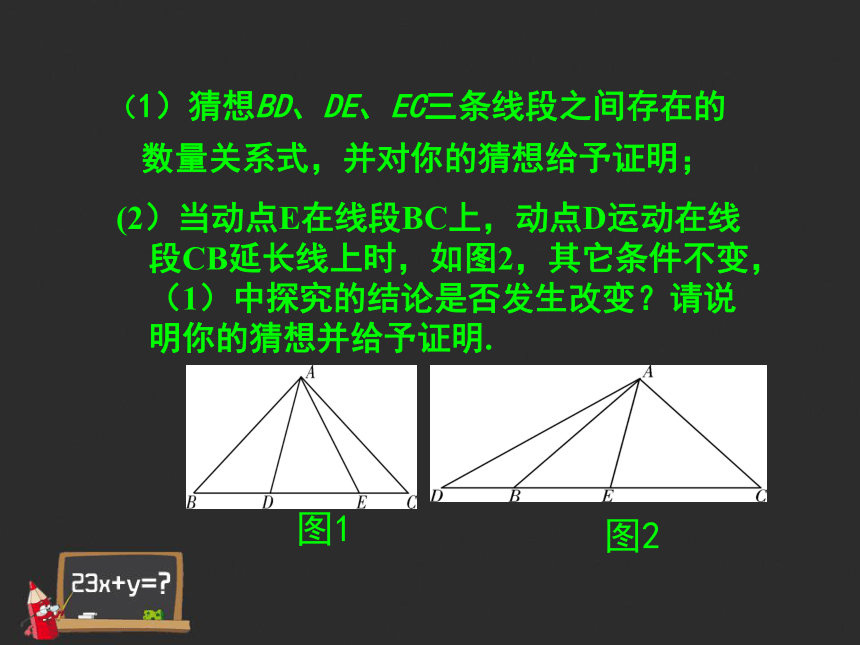
请你参考小明的思路探究并解决下列问题：（1）猜想BD、DE、EC三条线段之间存在的数量关系式，并对你的猜想给予证明； (2）当动点E在线段BC上，动点D运动在线段CB延长线上时，如图2，其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明.
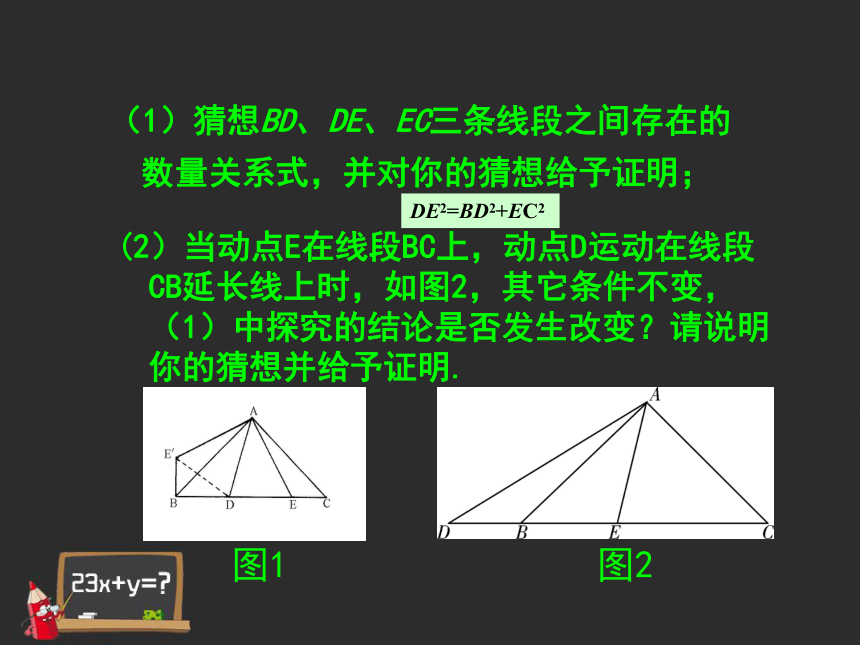
图2图1（1）猜想BD、DE、EC三条线段之间存在的数量关系式，并对你的猜想给予证明； 解：（1） DE2=BD2+EC2
证明：根据△AEC绕点A顺时针旋转90°
得到△ABE′ ∴ △AEC ≌△ABE′
∴ BE′=EC, AE′=AE ∠C=∠ABE′ ,
∠EAC=∠E’AB. 在Rt△ABC中
∵ AB=AC ∴ ∠ABC=∠ACB=45°
∴ ∠ABC＋∠ABE′=90°即 ∠E′BD=90°∴ E′B2＋BD2= ED2 又∵ ∠DAE=45° ∴ ∠BAD＋∠EAC=45°
∴ ∠E’AB＋∠BAD=45° 即 ∠E′AD=45°
∴ △AE′D≌△AED ∴ DE=DE′ ∴ DE2=BD2+EC2 （1）猜想BD、DE、EC三条线段之间存在的数量关系式，并对你的猜想给予证明； (2）当动点E在线段BC上，动点D运动在线段CB延长线上时，如图2，其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明.
图2图1DE2=BD2+EC2 （2）关系式DE2=BD2+EC2仍然成立
证明：将△ADB沿直线AD对折，得△AFD，连FE
∴ △AFD ≌△ABD ∴AF=AB，FD=DB
∠FAD=∠BAD，∠AFD=∠ABD
又∵AB=AC，∴AF=AC
∵∠FAE=∠FAD＋∠DAE=∠FAD＋45°
∠EAC =∠BAC－∠BAE=90°－(∠DAE－∠DAB)
= 45°＋∠DAB∴ ∠FAE =∠EAC又∵ AE=AE∴△AFE≌△ACE∴ FE=EC ∠AFE=∠ACE=45°
∠AFD=∠ABD=180°－∠ABC=135°
∴ ∠DFE=∠AFD－∠AFE=135°－45°=90°
∴在Rt△DFE中DF2＋FE2=DE2 , 即DE2=BD2 +EC2
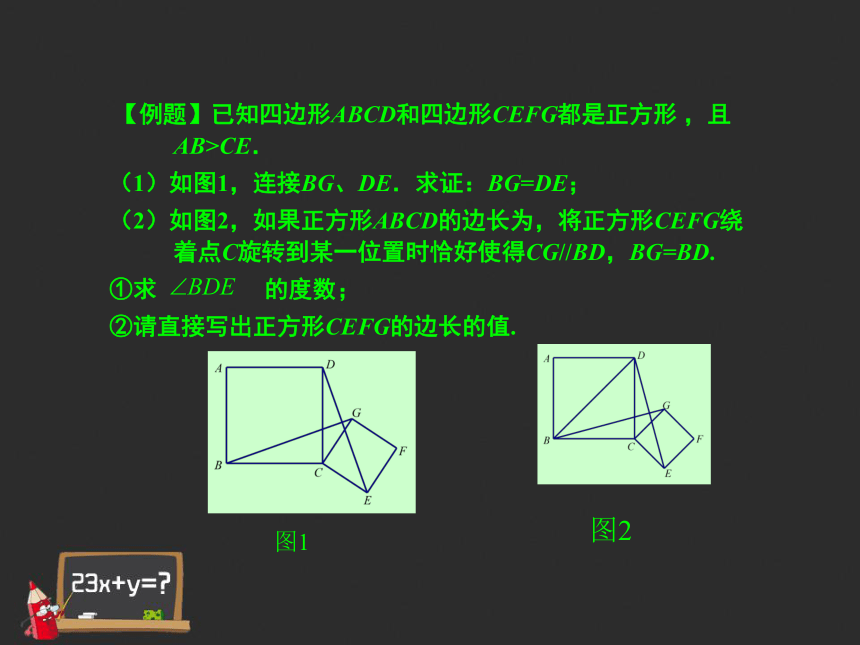
【例题】已知四边形ABCD和四边形CEFG都是正方形 ，且AB>CE．
（1）如图1，连接BG、DE．求证：BG=DE；
（2）如图2，如果正方形ABCD的边长为，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD，BG=BD.
①求 的度数；
②请直接写出正方形CEFG的边长的值.图1图2 【例题】已知四边形ABCD和四边形CEFG都是正方形 ，且AB>CE．
（1）如图1，连接BG、DE．求证：BG=DE；图1解：（1）证明：∵四边形ABCD和CEFG为正方形，
∴ , ,
∴
∴
∴ 【例题】已知四边形ABCD和四边形CEFG都是正方形 ，且AB>CE。
（2）如图2，如果正方形ABCD的边长为，将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD，BG=BD.
①求 的度数；
②请直接写出正方形CEFG的边长的值.（2）①连接BE .由（1）可知：BG=DE.
∵ ，∴
∴
∵
∴
∴∵
∴ ∴
∵ ∴
∴
②正方形的边长为 【代数、几何综合题】
代数、几何综合题是指需要运用代数、几何两部分知识解决的问题，是初中数学中知识覆盖面广、综合性最强的题型，它的解法多种多样。代数、几何综合题可以考查学生的数学基础知识和灵活运用知识的能力；考查对数学知识的迁移能力；考查将大题分解为小题、将复杂问题简单化的能力；考查对代数、几何知识的内在联系的认识，运用数学思想方法分析、解决问题的能力。 常见题型为：方程与几何综合题；函数与几何综合题；动态几何中的函数问题；直角坐标系的几何问题；几何图形中研究、分析、猜想与证明问题等。【例题】已知：直线 y=-2x-2与x轴交于点A，与y轴交于点C，抛物线经过点A、C、E，且点E（6，7）
（1）求抛物线的解析式.
（2）在直线AE的下方的抛物线取一点M使得构成的三角形AME的面积最大，请求出
M点的坐标及△AME的最大面积.
（3）若抛物线与x轴另一交点为B点，点P在x轴上，点D（1，-3），以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标．【例题】已知：直线 y=-2x-2与x轴交于点A，与y轴交于点C，抛物线经过点A、C、E，且点E（6，7）
（1）求抛物线的解析式.解：（1）∵直线y=-2x-2与x轴交于点A，与y轴交于点C
∴A（-1，0） C（0，-2）………1分
设抛物线的解析式为y=ax2+bx+c
∵抛物线经过点A、C、E
a-b+c=0 a=
∴ c=-2 ∴ b=
36a+6b+c=7 c=-2
∴【例题】已知：直线 y=-2x-2与x轴交于点A，与y轴交于点C，抛物线经过点A、C、E，且点E（6，7）
（2）在直线AE的下方的抛物线取一点M使得构成的三角形AME的面积最大，请求出M点的坐标及△AME的最大面积.（2）在抛物线上取一点M，作MN//y轴交AE于点N
设点M的横坐标为a，则纵坐标为
∵ MN//y轴 ∴点N的横坐标为a
设AE的解析式y=kx+b，把A（-1，0） E（6，7）代入y=kx+b中得 解得∵N在直线AE上，∴N(a ，a+1)
∴
∵ ∴ 时，MN有最大值
最大值
过点E作EH⊥x轴于点H 【例题】已知：直线 y=-2x-2与x轴交于点A，与y轴交于点C，抛物线经过点A、C、E，且点E（6，7）
（3）若抛物线与x轴另一交点为B点，点P在x轴上，点D（1，-3），以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标．（3）过点E作EF⊥X轴于点F，过点D作DM⊥X轴于点M
∵A(一1，0) B(4，0) E（6，7）
∴AO=1 BO=4 FO=6 FE=7 AB=5
∴AF=FE=7 ∠EAB=45° ∵D(1，-3 ) ∴DM=3 OM=1 MB=3
∴DM=MB=3 ∴∠MBD=45°
∴∠EAB=∠MBD 过点D作∠DP1B=∠AEB交X轴于点P1
∴ΔABE∽BDP1 AE:P1B=AB:BD
过点D作∠DP2B=∠ABE交X轴于点P2
∴ΔABE∽ΔBP2D ∴DB：AE=P2B：AB
∴【例题】如图，已知直线 与直线 相交于点C，l1、l2分别交x轴于A、B两点．矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．
（1）求△ABC的面积；
（2）求矩形DEFG的边DE与EF的长；
（3）若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t（0≤ t ≤ 12）秒，矩形DEGF与△ABC重叠部分的面积为S，求关于的函数t关系式，并写出相应的t的取值范围． 解决综合题的方法——分解变式。
即将综合题分解成多个有关联的较小的基本题，逐个解决，从而得到求解的目的。变式１: 求直线
与轴交点Ａ的坐标。【Ａ(-4,0)】
变式２：求直线
与轴交点Ｂ的坐标。【Ｂ(8,0)】变式３：已知直线
与直线 ,求交点Ｃ的坐标。【Ｃ(5,6)】
变式４：已知Ａ（-4,0），Ｂ（8,0），Ｃ(5,6)，求△ＡＢＣ的面积。变式５：已知ＢＤ//y轴，交直线
于点Ｄ，且Ｂ（8,0），求ＢＤ的长。
变式６：已知ＤＥ//x轴，交直线
于点Ｅ，且Ｄ（8,8），求ＤＥ的长【DE=4】 变式７：如图(1)，矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．已知Ａ(-4,0)，Ｂ(8,0)，Ｃ(5,6)，ＤＥ＝4。
若作ＣＭ⊥轴，垂足为Ｍ，
求ＭＡ。ＭＢ，ＭＦ的长。
MA=9,MB=3,MF=1. 变式８：如图(2),矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．已知Ａ(-4,0)，Ｂ(8,0)，Ｃ(5,6)，ＤＥ＝８。若作ＣＭ⊥x轴，垂足为Ｍ。若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于t（0≤t＜3）的函数关系式。 变式９：如图(3),矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．已知Ａ(-4,0)，Ｂ(8,0)，Ｃ(5,6)， ＤＥ＝８。若作ＣＭ⊥x轴，垂足为Ｍ。若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于t（3≤t＜8）的函数关系式。 变式10：如图(4),矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．已知Ａ(-4,0)，Ｂ(8,0)，Ｃ(5,6)， ＤＥ＝８。若作ＣＭ⊥x轴，垂足为Ｍ。若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于t（8≤t＜12）的函数关系式。综上所述 通过变式１到变式10的铺垫与解答，再解答原题难度会大大降低。显然，分解变式是综合问题简单化的重要途径，是解决综合问题的有效方法，可以增强学生解题的自信，培养学生分析问题、解决问题的能力。
解决几何综合题除了运用常规的思想和方法进行综合分析外，还常运用从特殊到一般、以静制动等解题策略。通过对特殊情况的研究联想、拓广到一般；从运动变化中探究不变的数学本质，再从不变的数学本质出发，寻求变化的规律,逐个击破。 *
【总结提升】 解决代数、几何综合题，一般以几何图形为载体，通过线段、角等图形寻找各元素之间的数量关系，建立代数中的方程或函数模型求解。也可以把数量关系与几何图形建立联系，使之直观化、形象化，从函数关系中点与点的位置、方程根的情况得出图形中的几何关系，以形导数，由数思形，从而寻求解题捷径。
祝同学们学习愉快，
取得优异成绩！