中考名家讲座第8讲中考数学备考策略——复习方法3
文档属性
| 名称 | 中考名家讲座第8讲中考数学备考策略——复习方法3 |  | |
| 格式 | zip | ||
| 文件大小 | 347.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-10 11:40:05 | ||
图片预览




文档简介
课件20张PPT。中考数学备考策略之
复习方法(三)执教人:吴晓燕变式1 如图,四边形ABCD是正方形,点M是AD边上 不同于A、D的点,
若sin∠ABM= ,
求证:P思路:构造等腰三角形,
利用相似证全等点N是CD的中点.∠NMB=∠MBC.H(三)一题多变,融会贯通如图,四边形ABCD是正方
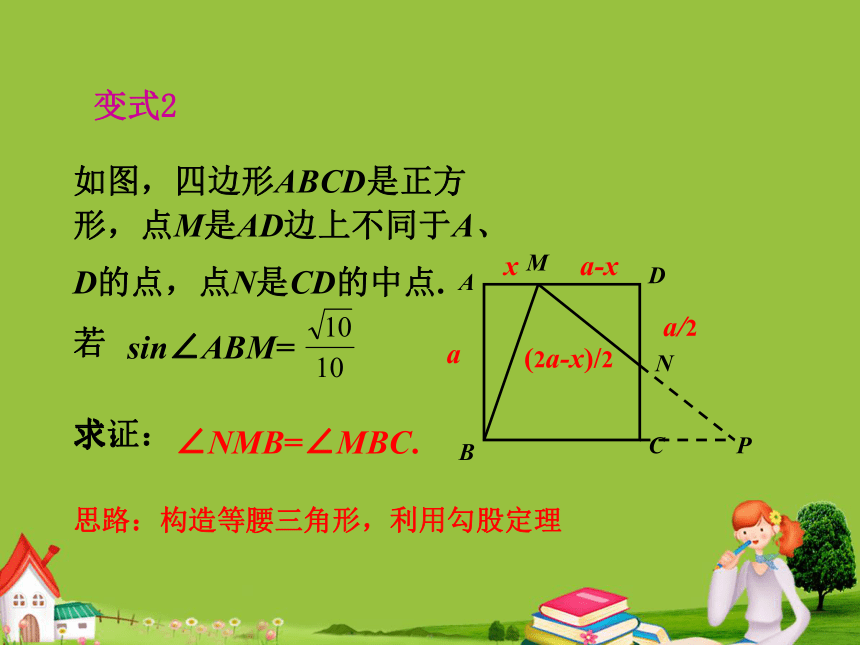
形,点M是AD边上不同于A、
D的点,点N是CD的中点.
若
求证:P思路:构造等腰三角形,利用勾股定理变式2∠NMB=∠MBC.sin∠ABM= 求:xa-xa/2(2a-x)/2a如图,正方形ABCD的边长为4,E为CD的中点,F为AD边上一点,且不与点D重合,AF=a.
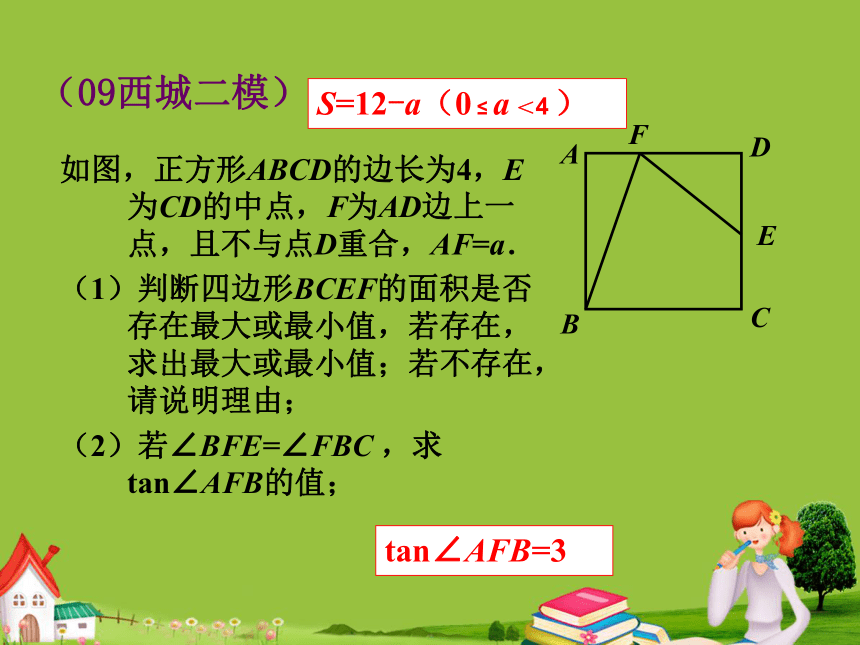
(1)判断四边形BCEF的面积是否存在最大或最小值,若存在,求出最大或最小值;若不存在,请说明理由;
(2)若∠BFE=∠FBC ,求tan∠AFB的值;(09西城二模)S=12-a(0 ≤ a <4 )tan∠AFB=3(2010丹东)如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,若DE=4cm,矩形ABCD的周长为32cm,求AE的长.ABCD FE(2010 上海)已知正方形中,点E在边CD上,ED=2,
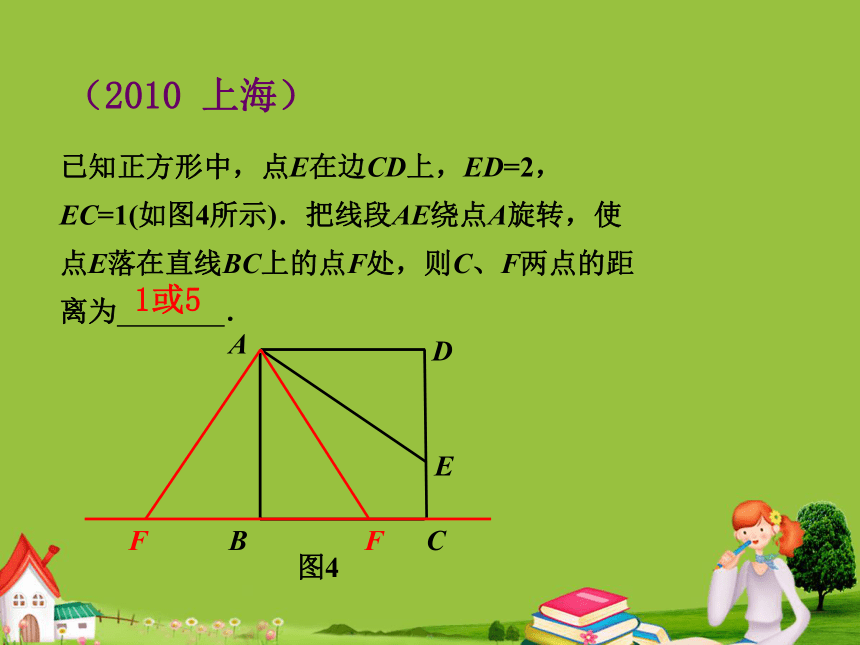
EC=1(如图4所示).把线段AE绕点A旋转,使
点E落在直线BC上的点F处,则C、F两点的距
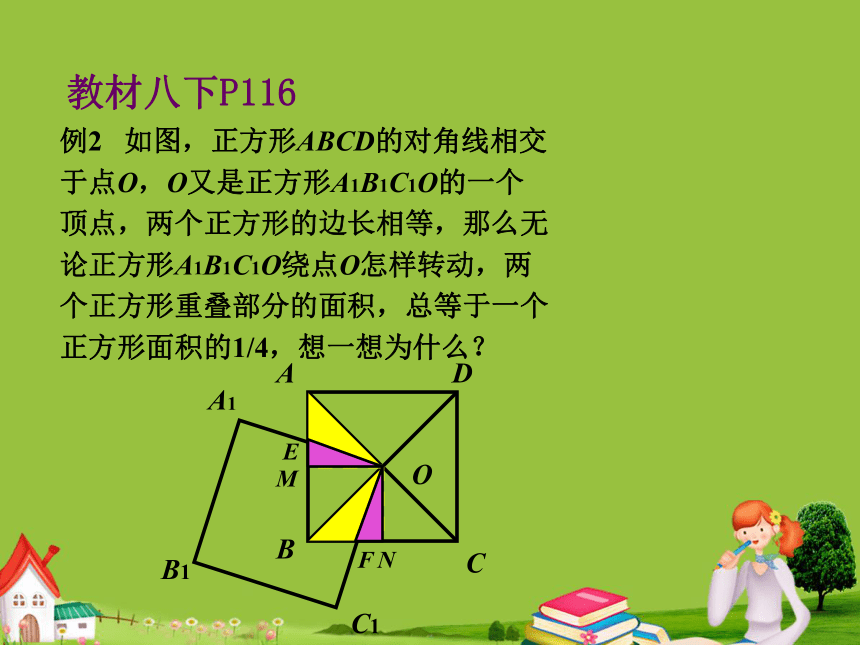
离为 .BCADE图41或5FF例2 如图,正方形ABCD的对角线相交
于点O,O又是正方形A1B1C1O的一个
顶点,两个正方形的边长相等,那么无
论正方形A1B1C1O绕点O怎样转动,两
个正方形重叠部分的面积,总等于一个
正方形面积的1/4,想一想为什么?ENM教材八下P116还能发现哪些结论?BE+BF=AB=√2 AO,AE=BF, ∠1= ∠ 2, 12⊿OEF是等腰直角三角形 34∠3+∠4=180° S四边形OEBF=1/4S正方形ABCD OE=OFBE=CF,引申三角形120°五边形 72°n边形? 拓广例3: 在一副三角板中,将一块含30°角的三
角板DEF的直角顶点D放在一块含45°角的三
角板ABC的斜边AC的中点上逆时针方向旋
转,直角三角板DEF的短直角边为DE,长直
角边为DF,且AB=BC=4.
(1)如图1,在上述旋转过程中,DM与DN,BM与CN有怎样的数量关系;
(2)在上述旋转过程中,两块三角板重叠出四边形DMBN的面积是否发生变化?若变化,如何变化;若不变,求出当时四边形DMBN的面积.
(临沂)图1αxy y=0.5x2-2x+4(0三角板的直角顶点与O点重合,转动三
角板使两直角边始终与BC、AB相交,
交点分别为M、N. 如果AB=4,AD=6,
OM=x,ON=y,则y与x的关系是 .ABCDOMNGHxy 例4:如图24-1,正方形ABCD和正方形QMNP, M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.
(1)猜想:ME 与MF的数量关系;(2)如图24-2,若将原题中的“正方形”为“菱形”,且∠M =∠B,其它条件不变,探索线段ME与线段MF的数量关系,并加以证明.(4)如下图,若将原题中的“正方
形”改为平行四边形,且∠M =∠B ,
AB:BC = m,其它条件不变,求出
ME:MF的值 .(直接写出答案)Thank You !祝同学们取得 好成绩!
复习方法(三)执教人:吴晓燕变式1 如图,四边形ABCD是正方形,点M是AD边上 不同于A、D的点,
若sin∠ABM= ,
求证:P思路:构造等腰三角形,
利用相似证全等点N是CD的中点.∠NMB=∠MBC.H(三)一题多变,融会贯通如图,四边形ABCD是正方
形,点M是AD边上不同于A、
D的点,点N是CD的中点.
若
求证:P思路:构造等腰三角形,利用勾股定理变式2∠NMB=∠MBC.sin∠ABM= 求:xa-xa/2(2a-x)/2a如图,正方形ABCD的边长为4,E为CD的中点,F为AD边上一点,且不与点D重合,AF=a.
(1)判断四边形BCEF的面积是否存在最大或最小值,若存在,求出最大或最小值;若不存在,请说明理由;
(2)若∠BFE=∠FBC ,求tan∠AFB的值;(09西城二模)S=12-a(0 ≤ a <4 )tan∠AFB=3(2010丹东)如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,若DE=4cm,矩形ABCD的周长为32cm,求AE的长.ABCD FE(2010 上海)已知正方形中,点E在边CD上,ED=2,
EC=1(如图4所示).把线段AE绕点A旋转,使
点E落在直线BC上的点F处,则C、F两点的距
离为 .BCADE图41或5FF例2 如图,正方形ABCD的对角线相交
于点O,O又是正方形A1B1C1O的一个
顶点,两个正方形的边长相等,那么无
论正方形A1B1C1O绕点O怎样转动,两
个正方形重叠部分的面积,总等于一个
正方形面积的1/4,想一想为什么?ENM教材八下P116还能发现哪些结论?BE+BF=AB=√2 AO,AE=BF, ∠1= ∠ 2, 12⊿OEF是等腰直角三角形 34∠3+∠4=180° S四边形OEBF=1/4S正方形ABCD OE=OFBE=CF,引申三角形120°五边形 72°n边形? 拓广例3: 在一副三角板中,将一块含30°角的三
角板DEF的直角顶点D放在一块含45°角的三
角板ABC的斜边AC的中点上逆时针方向旋
转,直角三角板DEF的短直角边为DE,长直
角边为DF,且AB=BC=4.
(1)如图1,在上述旋转过程中,DM与DN,BM与CN有怎样的数量关系;
(2)在上述旋转过程中,两块三角板重叠出四边形DMBN的面积是否发生变化?若变化,如何变化;若不变,求出当时四边形DMBN的面积.
(临沂)图1αxy y=0.5x2-2x+4(0
角板使两直角边始终与BC、AB相交,
交点分别为M、N. 如果AB=4,AD=6,
OM=x,ON=y,则y与x的关系是 .ABCDOMNGHxy 例4:如图24-1,正方形ABCD和正方形QMNP, M是正方形ABCD的对称中心,MN交AB于F,QM交AD于E.
(1)猜想:ME 与MF的数量关系;(2)如图24-2,若将原题中的“正方形”为“菱形”,且∠M =∠B,其它条件不变,探索线段ME与线段MF的数量关系,并加以证明.(4)如下图,若将原题中的“正方
形”改为平行四边形,且∠M =∠B ,
AB:BC = m,其它条件不变,求出
ME:MF的值 .(直接写出答案)Thank You !祝同学们取得 好成绩!
同课章节目录
