人教版数学7年级下册9.1.1不等式及其解集学案(无答案)
文档属性
| 名称 | 人教版数学7年级下册9.1.1不等式及其解集学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 85.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 11:31:27 | ||
图片预览

文档简介
9.1.1不等式及其解集
班级 姓名 学号
【学习目标】
1.了解不等式和一元一次不等式的概念.
2.理解不等式的解和解集,能正确表示不等式的解集.
3.体会不等式在生活中的应用.
教学重点:理解不等式、不等式的解和解集,一元一次不等式的意义,能正确列出不等式.
教学难点: 准确应用不等号,理解不等式的解和解集的意义.
【学习过程】
1、 问题诱思
任务(一)用不等式解决实际问题列出不等式
一辆匀速行驶的汽车在11:20时距离A地50千米,要在12:00以前驶过A地,车速应该具备什么条件?
题目中有等量关系吗?那是什么关系呢?
1.若设车速为每小时x千米,你能用一个式子表示上面的关系吗?
从时间上看 (1)
从路程上看 (2)
式子(1)、(2)从不同角度表示了车速应满足的条件.
用“<”、“>”、“≠”、“≥”、“≤”表示不等关系的式子叫做不等式.
练习:下列式子中是不等式的有
(1)a+b=b+a ; (2)-3>-5; (3)x≠l;
(4)x十3>6; (5) 2m< n ; (6)2x-3.
二、自主探究
任务(二)会判断不等式的解,不等式的解集
1.判断下列哪些数值能使不等式成立?
x . . . 72 75 78 80 ...
判断
想一想: 使不等式成立的数值还有没有? 有多少个?如果有,这些解应满足什么条件?
2.不等式的解:使不等式 的 的值叫做不等式的解.不等式的解有 个.
3.一般地,一个含有未知数的不等式的所有的解,组成这个不等式的 .如所有大于75的数组成不等式的解集,写作x >7 5,这个解集可以用数轴来表示.
4.求不等式的解集的过程叫做解不等式.
练习:下列数-3,-2,-1,0,1,2,3中, 不等式2x+3<5的解有 .
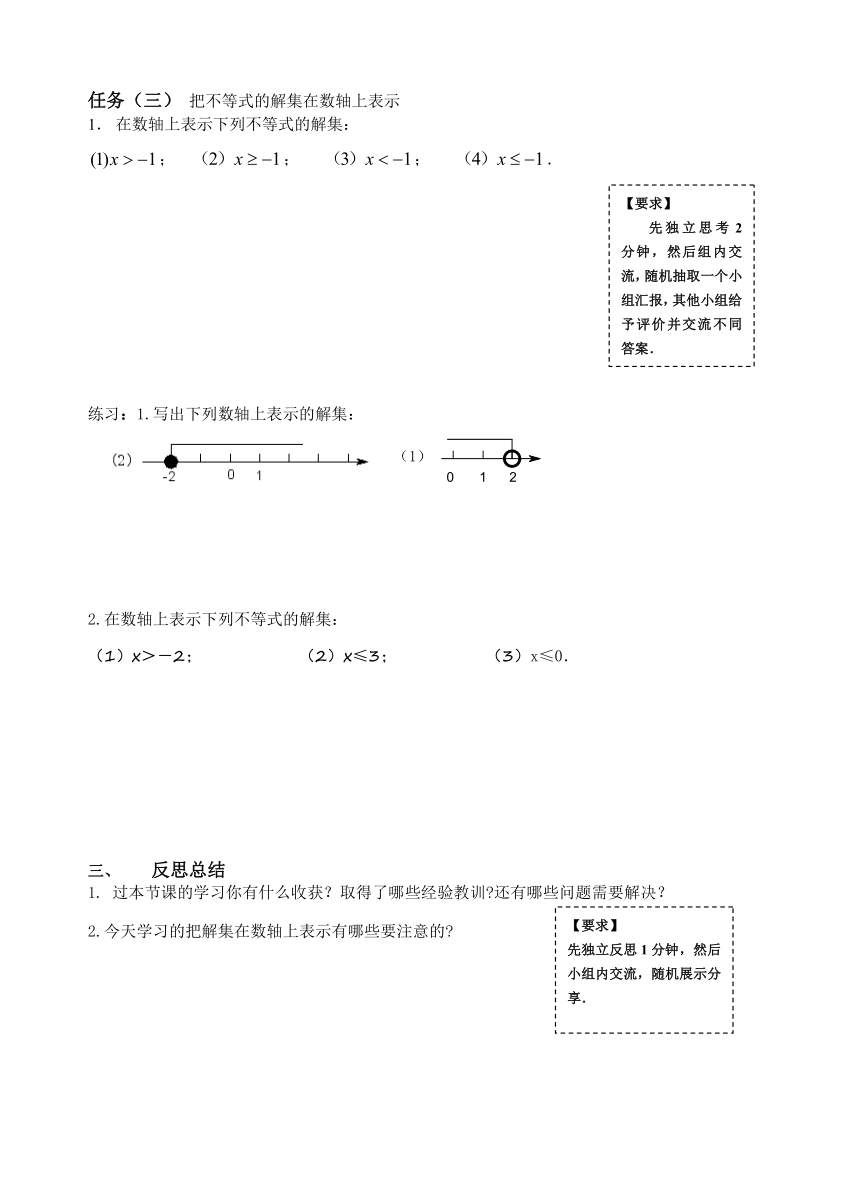
任务(三) 把不等式的解集在数轴上表示
1. 在数轴上表示下列不等式的解集:
; ; ; .
练习:1.写出下列数轴上表示的解集:
2.在数轴上表示下列不等式的解集:
(1)x>-2; (2)x≤3; (3)x≤0.
三、反思总结
1. 过本节课的学习你有什么收获?取得了哪些经验教训 还有哪些问题需要解决?
2.今天学习的把解集在数轴上表示有哪些要注意的
【课堂检测】 姓名 学号 得分
(A组)
1.下列式子中,,,,,中,是不等式的有( )个.
A.1 B. 2 C.3 D.4
2.下列说法中正确的是( )
A.x=3是不等式2x>1的解
B.x=3是不等式2x>1的唯一解
C.x=3不是不等式2x>1的解
D.x=3是不等式2x>1的解集
3.下列各项表示的是不等式的解集,其中错误的是( ).
4. (1)写出不等式x<4的所有正整数解:______________________.
(2)写出不等式x≥-3的所有负整数解:____________________.
(3) 写出不等式x≤3的所有非负整数解:____________________.
(4) 写出不等式x>-2的最小整数解:___________________.
5.某食品厂包装袋上标有“净含量385克±5克”,则食品的合格净含量范围是______________.
(B组)
6. 写出下列数轴上表示的解集:
7.在数轴上表示下列不等式的解集:
(1)x≤3; (2)0<x≤2;
(附加题)
已知正整数x满足,求的值.
【每日一题】
(1)①如果,那么a b;
②如果,那么a b;
③如果,那么a b.
(2)比较连个数的大小可以通过它们的差来判断,要将比较的两个数先做差计算,再根据差的符号来判断这两个数的大小。请根据(1)中的三个式子,用文字语言叙述出来。
(3)用(1)的方法能否比较与 大小?如果能,请写出比较过程。
【要求】
先独立思考2分钟,然后组内交流,随机抽取一个小组汇报,其他小组给予评价并交流不同答案.
o
75
【要求】
先独立思考2分钟,然后组内交流,随机抽取一个小组汇报,其他小组给予评价并交流不同答案.
【要求】
先独立反思1分钟,然后小组内交流,随机展示分享.
【要求】
独立完成,时间5分钟,组长做完后交老师批改,并批改组内成员的检测,组长完成后登分.
班级 姓名 学号
【学习目标】
1.了解不等式和一元一次不等式的概念.
2.理解不等式的解和解集,能正确表示不等式的解集.
3.体会不等式在生活中的应用.
教学重点:理解不等式、不等式的解和解集,一元一次不等式的意义,能正确列出不等式.
教学难点: 准确应用不等号,理解不等式的解和解集的意义.
【学习过程】
1、 问题诱思
任务(一)用不等式解决实际问题列出不等式
一辆匀速行驶的汽车在11:20时距离A地50千米,要在12:00以前驶过A地,车速应该具备什么条件?
题目中有等量关系吗?那是什么关系呢?
1.若设车速为每小时x千米,你能用一个式子表示上面的关系吗?
从时间上看 (1)
从路程上看 (2)
式子(1)、(2)从不同角度表示了车速应满足的条件.
用“<”、“>”、“≠”、“≥”、“≤”表示不等关系的式子叫做不等式.
练习:下列式子中是不等式的有
(1)a+b=b+a ; (2)-3>-5; (3)x≠l;
(4)x十3>6; (5) 2m< n ; (6)2x-3.
二、自主探究
任务(二)会判断不等式的解,不等式的解集
1.判断下列哪些数值能使不等式成立?
x . . . 72 75 78 80 ...
判断
想一想: 使不等式成立的数值还有没有? 有多少个?如果有,这些解应满足什么条件?
2.不等式的解:使不等式 的 的值叫做不等式的解.不等式的解有 个.
3.一般地,一个含有未知数的不等式的所有的解,组成这个不等式的 .如所有大于75的数组成不等式的解集,写作x >7 5,这个解集可以用数轴来表示.
4.求不等式的解集的过程叫做解不等式.
练习:下列数-3,-2,-1,0,1,2,3中, 不等式2x+3<5的解有 .
任务(三) 把不等式的解集在数轴上表示
1. 在数轴上表示下列不等式的解集:
; ; ; .
练习:1.写出下列数轴上表示的解集:
2.在数轴上表示下列不等式的解集:
(1)x>-2; (2)x≤3; (3)x≤0.
三、反思总结
1. 过本节课的学习你有什么收获?取得了哪些经验教训 还有哪些问题需要解决?
2.今天学习的把解集在数轴上表示有哪些要注意的
【课堂检测】 姓名 学号 得分
(A组)
1.下列式子中,,,,,中,是不等式的有( )个.
A.1 B. 2 C.3 D.4
2.下列说法中正确的是( )
A.x=3是不等式2x>1的解
B.x=3是不等式2x>1的唯一解
C.x=3不是不等式2x>1的解
D.x=3是不等式2x>1的解集
3.下列各项表示的是不等式的解集,其中错误的是( ).
4. (1)写出不等式x<4的所有正整数解:______________________.
(2)写出不等式x≥-3的所有负整数解:____________________.
(3) 写出不等式x≤3的所有非负整数解:____________________.
(4) 写出不等式x>-2的最小整数解:___________________.
5.某食品厂包装袋上标有“净含量385克±5克”,则食品的合格净含量范围是______________.
(B组)
6. 写出下列数轴上表示的解集:
7.在数轴上表示下列不等式的解集:
(1)x≤3; (2)0<x≤2;
(附加题)
已知正整数x满足,求的值.
【每日一题】
(1)①如果,那么a b;
②如果,那么a b;
③如果,那么a b.
(2)比较连个数的大小可以通过它们的差来判断,要将比较的两个数先做差计算,再根据差的符号来判断这两个数的大小。请根据(1)中的三个式子,用文字语言叙述出来。
(3)用(1)的方法能否比较与 大小?如果能,请写出比较过程。
【要求】
先独立思考2分钟,然后组内交流,随机抽取一个小组汇报,其他小组给予评价并交流不同答案.
o
75
【要求】
先独立思考2分钟,然后组内交流,随机抽取一个小组汇报,其他小组给予评价并交流不同答案.
【要求】
先独立反思1分钟,然后小组内交流,随机展示分享.
【要求】
独立完成,时间5分钟,组长做完后交老师批改,并批改组内成员的检测,组长完成后登分.
