2023—2024学年青岛版数学九年级上册4.1一元二次方程 课件(共15张PPT)
文档属性
| 名称 | 2023—2024学年青岛版数学九年级上册4.1一元二次方程 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 489.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 13:44:05 | ||
图片预览





文档简介
(共15张PPT)
第四章 一元二次方程
4.1一元二次方程(第1课时)
数学是研究现实生活中数量关系和空间形式的一门科学
——华罗庚
咱们学校操场上有一块面积为54平方米的长方形绿地,并且长比宽的2倍少3米,则绿地的长和宽是多少?
分析:设长方形绿地的宽为x米,则长为________。
根据等量关系:长×宽=长方形的面积
可以得到_________________________。
学习目标:
1.通过解决预学单的问题,总结一元一次方程的研究思路,体会方程问题的研究路径。
2.通过类比一元一次方程的学习路径,能够构建一元二次方程整章知识的脉络图,感悟类比的数学思想。
3.通过实际问题情境,抽象出一元二次方程的概念,会把一个一元二次方程转化成一般形式,并找出其中的二次项系数、一次项系数和
常数项。
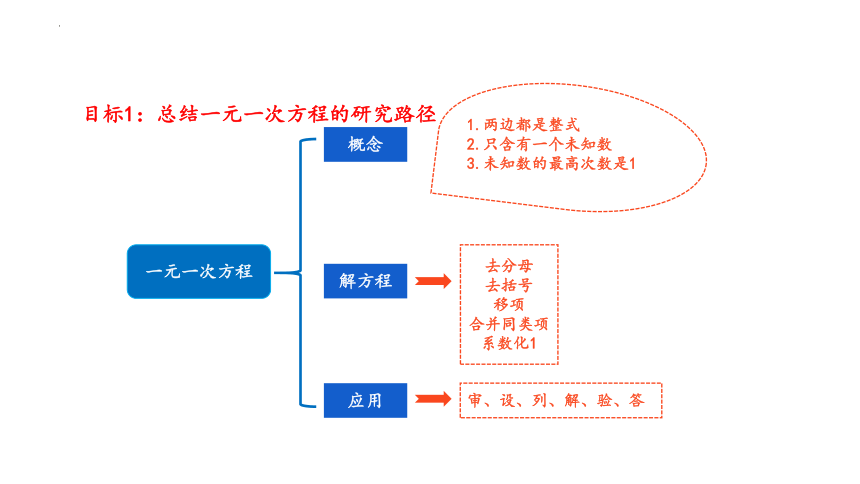
目标1:总结一元一次方程的研究路径
一元一次方程
概念
解方程
应用
1.两边都是整式
2.只含有一个未知数
3.未知数的最高次数是1
审、设、列、解、验、答
去分母
去括号
移项
合并同类项
系数化1
等式
解方程
方程
概念
解方程
应用
概念
解方程
应用
概念
解方程
方程应用
分式方程
一元一次方程
一元二次方程
类比研究
应用
由特殊到一般
1.两边都是整式
2.只含有一个未知数
3.未知数的最高次数是1
审、设、列、解、验、答
去分母
去括号
移项
合并同类项
系数化1
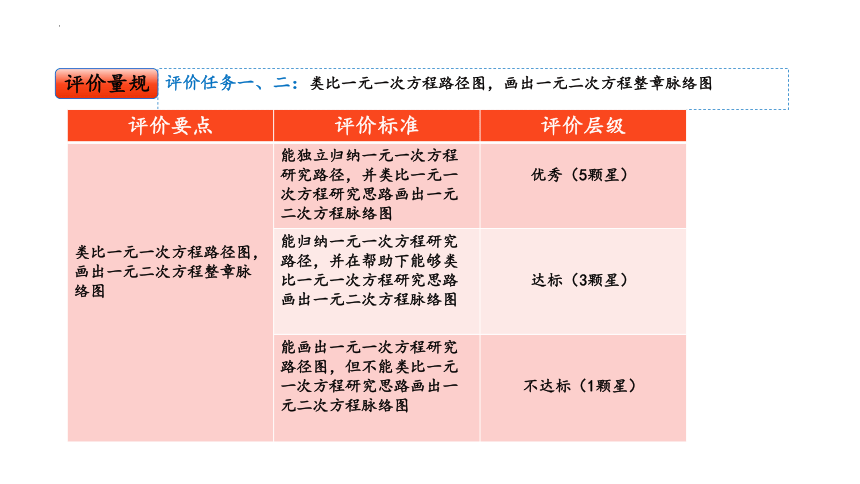
评价任务一、二:类比一元一次方程路径图,画出一元二次方程整章脉络图
评价量规
评价要点 评价标准 评价层级
类比一元一次方程路径图,画出一元二次方程整章脉络图 能独立归纳一元一次方程研究路径,并类比一元一次方程研究思路画出一元二次方程脉络图
优秀(5颗星)
能归纳一元一次方程研究路径,并在帮助下能够类比一元一次方程研究思路画出一元二次方程脉络图
达标(3颗星)
能画出一元一次方程研究路径图,但不能类比一元一次方程研究思路画出一元二次方程脉络图
不达标(1颗星)
目标3:理解一元二次方程的概念,掌握一元二次方程的一般形式
活动1:一元二次方程的概念
用方程描述下列问题中的数量关系:
(1)4个完全相同的正方形的面积之和是25,求正方形的边长。
(2)如图所示,长5m的梯子斜靠在墙上,梯子底端与墙的距离比梯子顶端与地面的距离多1m,求梯子底端距离墙角的水平距离。
(3)如图,点C是线段AB上的一点,且 ,求 的值。
A
C
B
问题1:观察列出的3个方程,他们与我们之前学习过的方程一样吗?如果不一样,最大的区别在哪里?
问题2:请化简3个方程,化简后按照x的降幂排列。
问题3:你能类比一元一次方程的定义,根据方程的特征尝试给他们下定义吗?
归纳总结:方程两边都是________,他们只含有________个未知数,并且整理后未知数的最高次数都是________,像这样的方程叫做一元二次方程。
整式
1
2
完成即时检测一
活动2:一元二次方程的一般形式
观察前面化简的方程:
你能类比一元一次方程的一般形式,给出一元二次方程的一般形式吗?
你能找出上述方程中的二次项、二次项系数、一次项、一次项系数、常数项吗?
典例剖析
例1:把方程 化为一元二次方程的一般形式,写出它的二次项、一次项、常数项及二次项系数、一次项系数。
完成即时检测二
总结——将一元二次方程化为一般形式的步骤:
1.去分母、去括号
2.移项、合并同类项
3.各项系数化成除1外无其他公约数的形式且保证二次项系数为正数
挑战自我:
a为何值时,方程 是一元二次方程?a为何值时是一元一次方程?
只有当二次项的系数 a≠0 时,方程 ax2+bx+c= 0 才是 一元二次方程.
完成即时检测三
评价任务三:能识别一元二次方程,并说出其中的二次项、一次项、二次项系数、一次项系数和常数项
评价量规
评价要点 评价标准 评价层级
能识别一元二次方程,并说出其中的二次项、一次项、二次项系数、一次项系数和常数项 能独立归纳一元二次方程概念,能将一个一元二次方程整理成一般形式,并正确说出其中的二次项、一次项、二次项系数、一次项系数和常数项,能根据一元二次方程的一般形式求字幕参数的值。
优秀(5颗星)
能在帮助下归纳一元二次方程概念及将一个一元二次方程整理成一般形式,并说出其中的二次项、一次项、二次项系数、一次项系数和常数项
达标(3颗星)
不能独立归纳一元二次方程概念,不能将一个一元二次方程整理成一般形式
不达标(1颗星)
拓展延伸
按照研究方程的“套路”,下面该谈谈一元二次方程的解法了,大家观察化简后的这几个方程:
哪一个方程最“好”解?(请解出来,并说明算理)
你能将其余方程转化为“好”解方程的形式吗?
课堂小结:
本节课你学到了哪些知识点?你还有什么收获?
第四章 一元二次方程
4.1一元二次方程(第1课时)
数学是研究现实生活中数量关系和空间形式的一门科学
——华罗庚
咱们学校操场上有一块面积为54平方米的长方形绿地,并且长比宽的2倍少3米,则绿地的长和宽是多少?
分析:设长方形绿地的宽为x米,则长为________。
根据等量关系:长×宽=长方形的面积
可以得到_________________________。
学习目标:
1.通过解决预学单的问题,总结一元一次方程的研究思路,体会方程问题的研究路径。
2.通过类比一元一次方程的学习路径,能够构建一元二次方程整章知识的脉络图,感悟类比的数学思想。
3.通过实际问题情境,抽象出一元二次方程的概念,会把一个一元二次方程转化成一般形式,并找出其中的二次项系数、一次项系数和
常数项。
目标1:总结一元一次方程的研究路径
一元一次方程
概念
解方程
应用
1.两边都是整式
2.只含有一个未知数
3.未知数的最高次数是1
审、设、列、解、验、答
去分母
去括号
移项
合并同类项
系数化1
等式
解方程
方程
概念
解方程
应用
概念
解方程
应用
概念
解方程
方程应用
分式方程
一元一次方程
一元二次方程
类比研究
应用
由特殊到一般
1.两边都是整式
2.只含有一个未知数
3.未知数的最高次数是1
审、设、列、解、验、答
去分母
去括号
移项
合并同类项
系数化1
评价任务一、二:类比一元一次方程路径图,画出一元二次方程整章脉络图
评价量规
评价要点 评价标准 评价层级
类比一元一次方程路径图,画出一元二次方程整章脉络图 能独立归纳一元一次方程研究路径,并类比一元一次方程研究思路画出一元二次方程脉络图
优秀(5颗星)
能归纳一元一次方程研究路径,并在帮助下能够类比一元一次方程研究思路画出一元二次方程脉络图
达标(3颗星)
能画出一元一次方程研究路径图,但不能类比一元一次方程研究思路画出一元二次方程脉络图
不达标(1颗星)
目标3:理解一元二次方程的概念,掌握一元二次方程的一般形式
活动1:一元二次方程的概念
用方程描述下列问题中的数量关系:
(1)4个完全相同的正方形的面积之和是25,求正方形的边长。
(2)如图所示,长5m的梯子斜靠在墙上,梯子底端与墙的距离比梯子顶端与地面的距离多1m,求梯子底端距离墙角的水平距离。
(3)如图,点C是线段AB上的一点,且 ,求 的值。
A
C
B
问题1:观察列出的3个方程,他们与我们之前学习过的方程一样吗?如果不一样,最大的区别在哪里?
问题2:请化简3个方程,化简后按照x的降幂排列。
问题3:你能类比一元一次方程的定义,根据方程的特征尝试给他们下定义吗?
归纳总结:方程两边都是________,他们只含有________个未知数,并且整理后未知数的最高次数都是________,像这样的方程叫做一元二次方程。
整式
1
2
完成即时检测一
活动2:一元二次方程的一般形式
观察前面化简的方程:
你能类比一元一次方程的一般形式,给出一元二次方程的一般形式吗?
你能找出上述方程中的二次项、二次项系数、一次项、一次项系数、常数项吗?
典例剖析
例1:把方程 化为一元二次方程的一般形式,写出它的二次项、一次项、常数项及二次项系数、一次项系数。
完成即时检测二
总结——将一元二次方程化为一般形式的步骤:
1.去分母、去括号
2.移项、合并同类项
3.各项系数化成除1外无其他公约数的形式且保证二次项系数为正数
挑战自我:
a为何值时,方程 是一元二次方程?a为何值时是一元一次方程?
只有当二次项的系数 a≠0 时,方程 ax2+bx+c= 0 才是 一元二次方程.
完成即时检测三
评价任务三:能识别一元二次方程,并说出其中的二次项、一次项、二次项系数、一次项系数和常数项
评价量规
评价要点 评价标准 评价层级
能识别一元二次方程,并说出其中的二次项、一次项、二次项系数、一次项系数和常数项 能独立归纳一元二次方程概念,能将一个一元二次方程整理成一般形式,并正确说出其中的二次项、一次项、二次项系数、一次项系数和常数项,能根据一元二次方程的一般形式求字幕参数的值。
优秀(5颗星)
能在帮助下归纳一元二次方程概念及将一个一元二次方程整理成一般形式,并说出其中的二次项、一次项、二次项系数、一次项系数和常数项
达标(3颗星)
不能独立归纳一元二次方程概念,不能将一个一元二次方程整理成一般形式
不达标(1颗星)
拓展延伸
按照研究方程的“套路”,下面该谈谈一元二次方程的解法了,大家观察化简后的这几个方程:
哪一个方程最“好”解?(请解出来,并说明算理)
你能将其余方程转化为“好”解方程的形式吗?
课堂小结:
本节课你学到了哪些知识点?你还有什么收获?
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
