专题7.7平面直角坐标系 全章复习与巩固 知识讲解(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题7.7平面直角坐标系 全章复习与巩固 知识讲解(含解析)2023-2024学年七年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 00:00:00 | ||
图片预览


文档简介
专题7.7 平面直角坐标系(全章复习与巩固)(知识讲解)
【学习目标】
1.理解平面直角坐标系及象限的概念,并会在坐标系中根据点的坐标描出点的位置、由点的位置写出它的坐标;
2.掌握用坐标系表示物体位置的方法及在物体平移变化前后点坐标的变化;
3.通过学习平面直角坐标系的基础知识,逐步理解平面内的点与有序实数对之间的一一对应关系,进而培养数形结合的数学思想.
【要点梳理】
要点一、有序数对
把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000),(17,190),(21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.
要点二、平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:
特别说明:
(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.
(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.
(3)要熟记坐标系中一些特殊点的坐标及特征:
①x轴上的点纵坐标为零;y轴上的点横坐标为零.
②平行于x轴直线上的点横坐标不相等,纵坐标相等;
平行于y轴直线上的点横坐标相等,纵坐标不相等.
③关于x轴对称的点横坐标相等,纵坐标互为相反数;
关于y轴对称的点纵坐标相等,横坐标互为相反数;
关于原点对称的点横、纵坐标分别互为相反数.
④象限角平分线上的点的坐标特征:
一、三象限角平分线上的点横、纵坐标相等;
二、四象限角平分线上的点横、纵坐标互为相反数.
注:反之亦成立.
(4)理解坐标系中用坐标表示距离的方法和结论:
①坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.
②x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1-x2|;
y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1-y2|.
③平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1-x2|;
平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1-y2|.
(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补.
要点三、坐标方法的简单应用
1.用坐标表示地理位置
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
特别说明:
(1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置.
(2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.
2.用坐标表示平移
(1)点的平移
点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).
特别说明:
上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换.
(2)图形的平移
在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
特别说明:
平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.
【典型例题】
类型一、平面直角坐标系 有序对 表示位置 表示路线
(2022秋·陕西宝鸡·八年级统考期中)
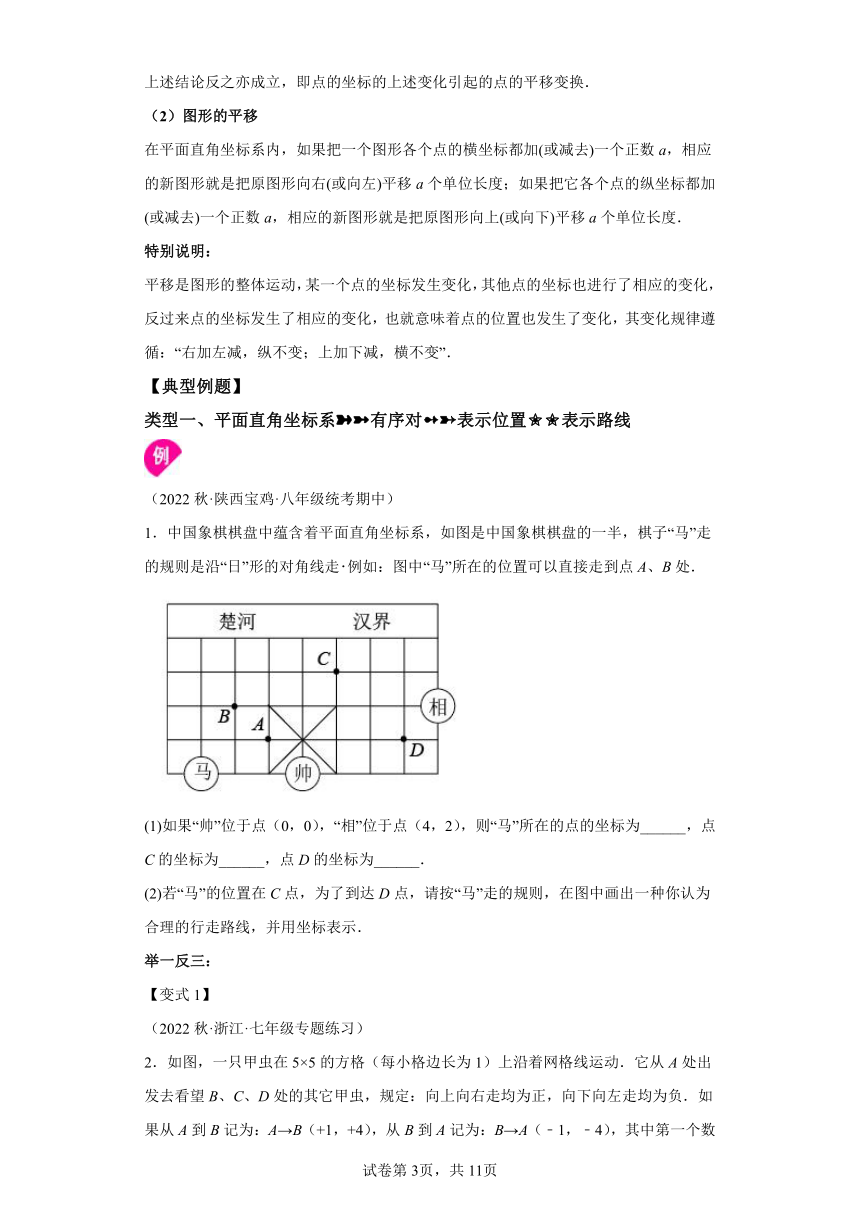
1.中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走例如:图中“马”所在的位置可以直接走到点A、B处.
(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为______,点C的坐标为______,点D的坐标为______.
(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,在图中画出一种你认为合理的行走路线,并用坐标表示.
举一反三:
【变式1】
(2022秋·浙江·七年级专题练习)
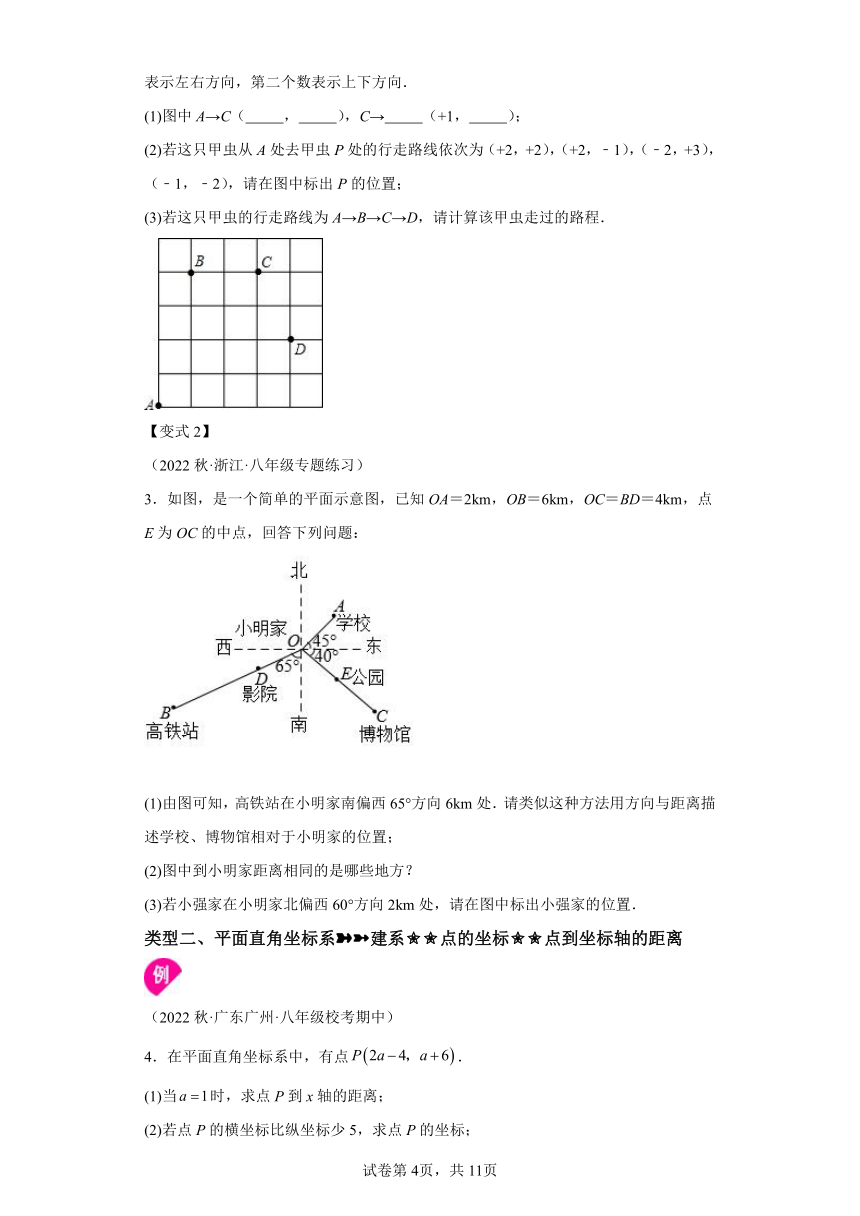
2.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
【变式2】
(2022秋·浙江·八年级专题练习)
3.如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
(3)若小强家在小明家北偏西60°方向2km处,请在图中标出小强家的位置.
类型二、平面直角坐标系 建系 点的坐标 点到坐标轴的距离
(2022秋·广东广州·八年级校考期中)
4.在平面直角坐标系中,有点.
(1)当时,求点P到x轴的距离;
(2)若点P的横坐标比纵坐标少5,求点P的坐标;
(3)点的坐标为,直线轴,求点P的坐标.
举一反三:
【变式1】
(2022秋·江苏·八年级专题练习)
5.已知点Q,试分别根据下列条件,回答问题.
(1)若点Q在y轴上,求点Q的坐标.
(2)若点Q在(即第一象限)角平分线上,求点Q的坐标.
【变式2】
(2022春·河南信阳·七年级校考阶段练习)
6.已知以下点的坐标,,,.
(1)在平面直角坐标系中标出点,,的位置.
(2)求三角形的面积.
(3)若点在轴上,且三角形的面积与三角形的面积相等,求点的坐标.
类型三、平面直角坐标系 几何图形 面积问题
(2023秋·北京海淀·七年级人大附中校考期末)
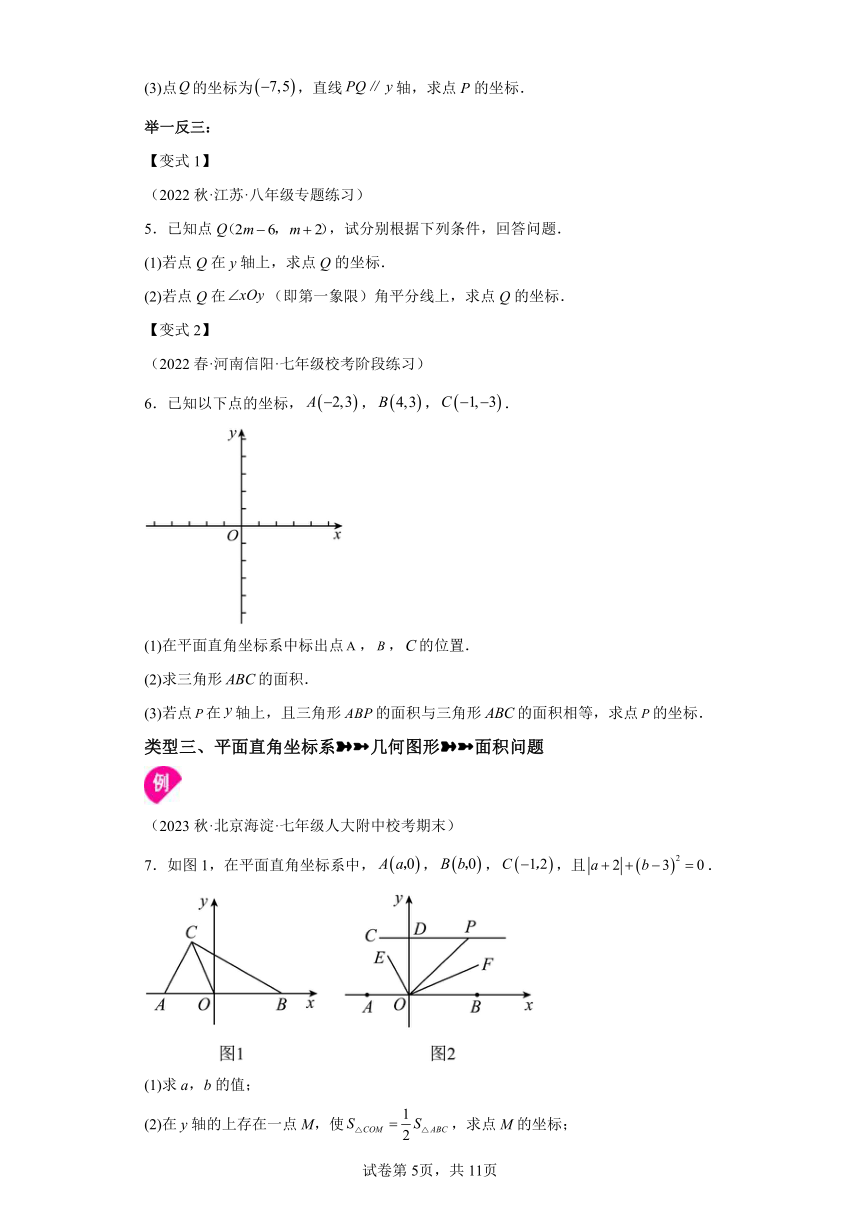
7.如图1,在平面直角坐标系中,,,,且.
(1)求a,b的值;
(2)在y轴的上存在一点M,使,求点M的坐标;
(3)如图2,过点C作轴交y轴于点D,点P为线段延长线上一动点,连接平分,.当点P运动时的值是否会改变?若不变,求其值;若改变,说明理由.
举一反三:
【变式1】
(2022秋·广东广州·八年级广州市第四十一中学校考期末)
8.如图,在平面直角坐标系中,已知,,其中,满足.
(1)填空:______,________;
(2)若存在一点,点M到x轴距离_______,到y轴距离_______,求的面积(用含m的式子表示);
(3)在(2)条件下,当时,在y轴上有一点P,使得的面积与的面积相等,请求出点P的坐标.
【变式2】
(2022秋·北京海淀·八年级北京育英中学校考期末)
9.如图,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)若线段与轴交于点,在轴上是否存在点,使得三角形和三角形的面积相等,若存在,求出点坐标;若不存在,请说明理由;
类型四、平面直角坐标系 判断点的位置 参数
(2022秋·江苏南京·八年级校考阶段练习)
10.如图,在平面直角坐标系中,A、B、C三点的坐标分别为.
(1)画出;
(2)面积为 ___________;
(3)如图,是由经过平移得到的.已知点为内的一点,则点P在内的对应点的坐标是 ___________.
举一反三:
【变式1】
(2022春·福建厦门·七年级统考期末)
11.在平面直角坐标系中,O为原点,点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
(1)求b和k的值;(用含a的代数式表示k)
(2)探求当a变化时,三角形与三角形的面积大小关系.
【变式2】
(2022秋·八年级课时练习)
12.在直角坐标系中,已知线段,点A的坐标为,点B的坐标为,如图1所示.
(1)平移线段到线段,使点A的对应点为D,点B的对应点为C,若点C的坐标为,求点D的坐标;
(2)平移线段到线段,使点C在y轴的正半轴上,点D在第二象限内,连接,,如图2所示.若(表示三角形的面积),求点C、D的坐标.
(3)在(2)的条件下,在y轴上是否存在一点P,使(表示三角形的面积)?若存在,求出点P的坐标;若不存在,请说明理由.
类型五、平面直角坐标系 图形的变换 对称问题
(2021秋·河北邢台·八年级统考期末)
13.如图,直角坐标系中,在边长为的正方形网格中,的顶点均在格点上,点,的坐标分别是,.
(1)请在图中画出关于轴的对称,点的坐标为______,点的坐标为______ ;
(2)请写出点关于轴的对称点的坐标为______;
(3)求的面积.
举一反三:
【变式1】
(2023秋·山东烟台·七年级统考期末)
14.如图,在直角坐标系中,的位置如图所示,请完成下列问题:
(1)分别写出点A,点C的坐标;
(2)作出关于x轴的对称图形,并写出的坐标为 .
(3)求的面积;
(4)在y轴上找一点P,使最小.
【变式2】
(2022秋·河北邯郸·八年级统考期中)
15.在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形(三角形的三个顶点都在小正方形上)
(1)画出关于直线:的对称三角形;并写出,,的坐标;
(2)在直线上找一点,使最小,满足条件的点为______.提示:直线是过点且垂直于轴的直线.
类型六、平面直角坐标系 中考真题
(2022·陕西·统考中考真题)
16.如图,的顶点坐标分别为.将平移后得到,且点A的对应点是,点B、C的对应点分别是.
(1)点A、之间的距离是__________;
(2)请在图中画出.
举一反三:
【变式1】
(2019·广西·统考中考真题)
17.如图,在平面直角坐标系中,已知的三个顶点坐标分别是
(1)将向上平移4个单位长度得到,请画出;
(2)请画出与关于轴对称的;
(3)请写出的坐标.
【变式2】
(2015·广西崇左·中考真题)
18.如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1),,
(2)路线见解析,走路线为
【分析】(1)结合图示,确定原点,再根据题意求出点的位置;
(2)结合图示,确定原点,再根据题意求出马走的路线.
【详解】(1)解:∵“帅”位于点(0,0),“相”位于点(4,2),
∴“马”所在的点的坐标为(-3,0),
点C的坐标为(1,3),
点D的坐标为(3,1).
故答案为,,.
(2)解:以 “帅”为(0,0),则“马”走的路线为,
如图:
.
【点睛】本题考查了用有序数对解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置.
2.(1)+3,+4,D,﹣2
(2)见解析
(3)10
【分析】(1)根据规定及实例可知A→C记为(3,4),C→D记为(1,﹣2);
(2)按题目所示平移规律分别向右向上平移2个格点,再向右平移2个格点,向下平移1个格点;向左平移2个格点,向上平移3个格点;向左平移1个向下平移两个格点即可得到点P的坐标,在图中标出即可.
(3)根据点的运动路径,表示出运动的距离,相加即可得到行走的总路径长.
【详解】(1)解:(1)∵规定:向上向右走为正,向下向左走为负,
∴A→C记为(+3,+4),C→D记为(+1,﹣2).
故答案为:+3,+4,D,﹣2;
(2)P点位置如图所示.
(3)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2).
则该甲虫走过的路线长为1+4+2+1+2=10.
【点睛】本题主要考查了利用坐标确定点的位置的方法,解题的关键是正确的理解从一个点到另一个点移动时,如何用坐标表示.
3.(1)学校在小明家北偏东45°方向2km处,博物馆在小明家南偏东50°方向4 km处
(2)图中到小明家距离相同的是学校和公园和影院
(3)见解析
【分析】(1)由图可知,学校在小明家北偏东45°方向2km处,博物馆在小明家南偏东50方向4km处;
(2)观察图形,根据OA, OE, OD的长度及图中各角度,即可得出结论.
(3)作北偏西60°角,取OE = 2即可.
【详解】(1)解:学校在小明家北偏东45°方向2km处,博物馆在小明家南偏东50°方向4 km处;
(2)图中到小明家距离相同的是学校和公园和影院;
(3)如图,点F即为小强家.
【点睛】本题考查了方向角,解题的关键是熟练掌握运用方位角及确定位置需要两个元素.
4.(1)7
(2)
(3)
【分析】(1)根据得点P的坐标为,即可得到点P到x轴的距离;
(2)列得,求出a即可;
(3)根据直线轴,得到,求出a即可.
【详解】(1)解:当时,点P的坐标为,
∴点P到x轴的距离为7;
(2),
解得,
∴点P的坐标为;
(3)∵直线轴,
∴,
解得,
∴点P的坐标为.
【点睛】此题考查了点到坐标轴的距离,平行于坐标轴的点的坐标特点,解一元一次方程,正确理解坐标与图形的关系是解题的关键.
5.(1);
(2).
【分析】(1)根据y轴上的点的横坐标等于零,可得,即可求出m的值,进而得到答案;
(2) 根据点Q到两坐标的距离相等,可得关于m的方程,解方程即可得出答案.
【详解】(1)解:点Q在y轴上,则,
解得,
所以;
故Q点的坐标为 ;
(2)解:当点Q在(即第一象限)角平分线上,即:,
解得:,
所以,
故Q点的坐标为:.
【点睛】本题考查了点的坐标,y轴上的点的横坐标等于零,在角平分线上点到两坐标轴距离相等.
6.(1)见解析
(2)18
(3)(0,-3)或(0,9)
【分析】(1)根据点的坐标直接确定出点A、B、C的位置即可;
(2)根据三角形的面积求解可得;
(3)设P(0,m),利用三角形ABP的面积与三角形ABC的面积相等,求出m值,进而得出答案.
【详解】(1)解:如图所示,
(2)解:∵A(-2,3),,,
,点到AB的距离是;
的面积是:;
(3)解: ∵A(-2,3),,
∴ABx轴,
设P(0,m),
∵点在轴上,且三角形的面积与三角形的面积相等,
∴,
解得:m=-3或m=9,
∴点的坐标为:(0,-3)或(0,9).
【点睛】本题考查坐标与图形性质,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答.
7.(1)
(2)或,
(3)的值是定值,,理由见解析
【分析】(1)根据绝对值和平方的非负性,即可进行解答;
(2)先根据A、B、C的坐标求出求出的值,再根据y轴上点的坐标特征,设,最后根据三角形的面积公式将表示出来即可;
(3)根据,得出,,再根据平分得出,进而得出,最后根据平行线的性质得出即可得出结论.
【详解】(1)解:∵,
∴,则,
∴;
(2)由(1)可知,
∴,
∵,
∴点C到x轴距离为2,
∴,
∵当M在y轴上时,
∴设,
∴,
∵,
∴,
∴,
∴或,
(3)如图2中,结论:的值是定值,
理由:∵,
∴,
∴,,
∵平分,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
【点睛】本题主要考查了非负数的性质,坐标与图形,平行线的性质,角平分线的定义,解题的关键是掌握相关知识点并灵活运用.
8.(1),3
(2),2,
(3)或
【分析】(1)可将变形为,再根据平方和绝对值的非负性即可求出a和b的值;
(2)由M点坐标即可直接得出点M到x轴距离为,到y轴距离为.又可求出,即可利用三角形面积公式求出;
(3)将代入,得.设,则.即得出,解出t的值,即得出点P的坐标.
【详解】(1)∵,
∴,
∴,解得:.
故答案为:,3;
(2)∵,
∴点M到x轴距离为,到y轴距离为.
由(1)可知,,
∴,
∴.
故答案为:,2,;
(3)当时,.
设,
∴.
∵,
∴,
解得:,
∴或.
【点睛】本题考查非负数的性质,点到坐标轴的距离,坐标与图形.利用数形结合的思想是解题关键.
9.(1)36
(2)或
【分析】(1)先根据非负数的性质求出,的值,进而得出,两点的坐标,根据三角形的面积公式即可得出结论;
(2)设,利用三角形和三角形的面积相等可得到关于的方程,再解方程求出即可得点坐标.
【详解】(1),
,,
解得,,
,,
轴,
,
,,
;
(2)设,
,
,
三角形和三角形的面积相等,,
,
,即,
解得:或,
或;
【点睛】本题昰三角形综合题,考查了非负数的性质、坐标与图形性质以及三角形面积公式,理解坐标与长度的关系是解题的关键.
10.(1)见解析
(2)8
(3)
【分析】(1)根据题意,画出,即可求解;
(2)用所在的长方形的面积减去其周围的三个三角形的面积,即可求解;
(3)根据题意得:是由先向右平移4个单位,再向下平移3个单位得到的,即可求解.
【详解】(1)解:如图,即为所求;
(2)解:的面积;
故答案为:8;
(3)解:根据题意得:是由先向右平移4个单位,再向下平移3个单位得到的,
∴点P在内的对应点的坐标是.
故答案为:
【点睛】本题主要考查了坐标与图形,图形变换,熟练掌握图形平移的性质是解题的关键.
11.(1);;
(2)
【分析】(1)由,,结合,可得线段向上平移,再根据点的平移规则列方程即可;
(2)由平移的性质可得:,,如图,可得,过作于,过作于,显然,,从而可得答案.
【详解】(1)解:如图,∵点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
∴,,
∴,即,解得:,
∴,,,
∴,
解得:;
(2)由平移的性质可得:,,如图,
∴,
过作于,过作于,
显然,
∴,
∴,
∴.
【点睛】本题考查的是平移的性质,点的平移的坐标变化规律,平移的性质,平行线的性质,熟练地利用平移的性质解题是关键.
12.(1);
(2),;
(3)存在点P,其坐标为或.
【分析】(1)利用平移的性质确定出平移的方向和距离,进而可得点D的坐标;
(2)设D点纵坐标为y,由平移的性质可得,,然后根据建立方程求出y的值即可;
(3)设出点P的坐标,表示出,然后根据建立方程求解即可.
【详解】(1)解:∵平移后的对应点为,
∴点B向左平移了5个单位长度,向上平移了4个单位长度,
∴A点平移后的对应点;
(2)解:设D点纵坐标为y,
∵点C在y轴上,点D在第二象限,
∴线段向左平移3个单位长度,向上平移个单位长度,
∴,,
连接,
则,
即
解得:,
∴,;
(3)解:设点,
∴,
∵,
∴,
∴,
∴或,
∴存在点P,其坐标为或.
【点睛】此题是几何变换综合题,主要考查了平移的性质,坐标与图形性质,解本题的关键是平移性质的灵活运用,用面积关系建立方程.
13.(1);;
(2)
(3)
【分析】(1)根据网格结构找出点、的位置,然后与点顺次连接即可,再根据平面直角坐标系写出点、的坐标;
(2)根据关于轴对称的点的横坐标相同,纵坐标互为相反数写出即可;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
【详解】(1)解:如图所示;点,;
故答案为:;;
(2)由图象可知:;
故答案为:.
(3),
,
.
【点睛】本题考查了利用轴对称变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.
14.(1),
(2)作图见解析,
(3)3.5
(4)作图见解析
【分析】(1)根据点的坐标的表示方法求解;
(2)利用关于y轴对称的点的坐标特征得到的坐标,然后描点连线即可;
(3)用一个矩形的面积分别减去三个直角三角形的面积去计算的面积;
(4)作点B关于x轴的对称点,连接交x轴于P点,利用两点之间线段最短可判断P点满足条件.
【详解】(1)解:由图形可知:;
(2)如下图,作点A、B、C关于y轴对称的点的坐标特征得到,连接即为所求;
(3)由题意可知:的面积;
(4)如(2)图,作点B关于x轴的对称点,连接交x轴于P点,
两点之间线段最短,
最小,
点P即为所求.
【点睛】本题考查了利用轴对称变换作图,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.
15.(1)图见解析,,,
(2)图见解析,点的坐标为
【分析】(1)分别作出点,,关于直线:的对称的点,然后顺次连接,并写出,,的坐标;
(2)作出点关于对称的点,连接,与的交点即为点,此时最小,写出点的坐标即可.
【详解】(1)解:如图,分别作出点,,关于直线:的对称的点,,,
连接,,,
则即为所作,
∴,,.
(2)如图,作点关于直线对称的点,连接,与直线的交点即为点,
∴直线为线段的垂直平分线,
∴,
∴,
∴此时最小,点坐标为.
故答案为:.
【点睛】本题考查根据轴对称变换作图,最短路线问题.解答本题的关键是根据网格结构作出对应点的位置并顺次连接.
16.(1)4
(2)见解析
【分析】(1)由得,A、之间的距离是2-(-2)=4;
(2)根据题意找出平移规律,求出,进而画图即可.
【详解】(1)解:由得,
A、之间的距离是2-(-2)=4.
故答案为:4.
(2)解:由题意,得,
如图,即为所求.
【点睛】本题考查了坐标系中两点之间的距离求解以及平移求点坐标画图,题目相对较简单,掌握平移规律是解决问题的关键.
17.(1)如图所示:,即为所求;见解析;(2)如图所示:,即为所求;见解析;(3).
【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用轴对称的性质得出对应点位置进而得出答案;
(3)利用所画图象得出对应点坐标.
【详解】(1)如图所示:,即为所求;
(2)如图所示:,即为所求;
(3).
【点睛】此题主要考查了轴对称变换以及平移变换,正确得出对应点位置是解题关键.
18.(1)作图见试题解析,A(-3,1), B(0,2),C(-1,4);(2)2.
【分析】(1)△A1B1C1是由△ABC向右平移4个单位得到的,故将△A1B1C1向左平移4个单位既是△ABC;
(2)由平移性质知,A1A平行于x轴,且等于平移距离4,△A1OA边A1OA上的高可点A1的坐标确定.
【详解】解:(1)A(-3,1), B(0,2),C(-1,4),如图:
(2)A1A=4,
∴=A1A×1=×4×1=2.
答案第1页,共2页
答案第1页,共2页
【学习目标】
1.理解平面直角坐标系及象限的概念,并会在坐标系中根据点的坐标描出点的位置、由点的位置写出它的坐标;
2.掌握用坐标系表示物体位置的方法及在物体平移变化前后点坐标的变化;
3.通过学习平面直角坐标系的基础知识,逐步理解平面内的点与有序实数对之间的一一对应关系,进而培养数形结合的数学思想.
【要点梳理】
要点一、有序数对
把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000),(17,190),(21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.
要点二、平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系,如下图:
特别说明:
(1)坐标平面内的点可以划分为六个区域:x轴,y轴、第一象限、第二象限、第三象限、第四象限,这六个区域中,除了x轴与y轴有一个公共点(原点)外,其他区域之间均没有公共点.
(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.
(3)要熟记坐标系中一些特殊点的坐标及特征:
①x轴上的点纵坐标为零;y轴上的点横坐标为零.
②平行于x轴直线上的点横坐标不相等,纵坐标相等;
平行于y轴直线上的点横坐标相等,纵坐标不相等.
③关于x轴对称的点横坐标相等,纵坐标互为相反数;
关于y轴对称的点纵坐标相等,横坐标互为相反数;
关于原点对称的点横、纵坐标分别互为相反数.
④象限角平分线上的点的坐标特征:
一、三象限角平分线上的点横、纵坐标相等;
二、四象限角平分线上的点横、纵坐标互为相反数.
注:反之亦成立.
(4)理解坐标系中用坐标表示距离的方法和结论:
①坐标平面内点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.
②x轴上两点A(x1,0)、B(x2,0)的距离为AB=|x1-x2|;
y轴上两点C(0,y1)、D(0,y2)的距离为CD=|y1-y2|.
③平行于x轴的直线上两点A(x1,y)、B(x2,y)的距离为AB=|x1-x2|;
平行于y轴的直线上两点C(x,y1)、D(x,y2)的距离为CD=|y1-y2|.
(5)利用坐标系求一些知道关键点坐标的几何图形的面积:切割、拼补.
要点三、坐标方法的简单应用
1.用坐标表示地理位置
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
特别说明:
(1)我们习惯选取向东、向北分别为x轴、y轴的正方向,建立坐标系的关键是确定原点的位置.
(2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.
2.用坐标表示平移
(1)点的平移
点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).
特别说明:
上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换.
(2)图形的平移
在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
特别说明:
平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.
【典型例题】
类型一、平面直角坐标系 有序对 表示位置 表示路线
(2022秋·陕西宝鸡·八年级统考期中)
1.中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走例如:图中“马”所在的位置可以直接走到点A、B处.
(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为______,点C的坐标为______,点D的坐标为______.
(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,在图中画出一种你认为合理的行走路线,并用坐标表示.
举一反三:
【变式1】
(2022秋·浙江·七年级专题练习)
2.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
【变式2】
(2022秋·浙江·八年级专题练习)
3.如图,是一个简单的平面示意图,已知OA=2km,OB=6km,OC=BD=4km,点E为OC的中点,回答下列问题:
(1)由图可知,高铁站在小明家南偏西65°方向6km处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;
(2)图中到小明家距离相同的是哪些地方?
(3)若小强家在小明家北偏西60°方向2km处,请在图中标出小强家的位置.
类型二、平面直角坐标系 建系 点的坐标 点到坐标轴的距离
(2022秋·广东广州·八年级校考期中)
4.在平面直角坐标系中,有点.
(1)当时,求点P到x轴的距离;
(2)若点P的横坐标比纵坐标少5,求点P的坐标;
(3)点的坐标为,直线轴,求点P的坐标.
举一反三:
【变式1】
(2022秋·江苏·八年级专题练习)
5.已知点Q,试分别根据下列条件,回答问题.
(1)若点Q在y轴上,求点Q的坐标.
(2)若点Q在(即第一象限)角平分线上,求点Q的坐标.
【变式2】
(2022春·河南信阳·七年级校考阶段练习)
6.已知以下点的坐标,,,.
(1)在平面直角坐标系中标出点,,的位置.
(2)求三角形的面积.
(3)若点在轴上,且三角形的面积与三角形的面积相等,求点的坐标.
类型三、平面直角坐标系 几何图形 面积问题
(2023秋·北京海淀·七年级人大附中校考期末)
7.如图1,在平面直角坐标系中,,,,且.
(1)求a,b的值;
(2)在y轴的上存在一点M,使,求点M的坐标;
(3)如图2,过点C作轴交y轴于点D,点P为线段延长线上一动点,连接平分,.当点P运动时的值是否会改变?若不变,求其值;若改变,说明理由.
举一反三:
【变式1】
(2022秋·广东广州·八年级广州市第四十一中学校考期末)
8.如图,在平面直角坐标系中,已知,,其中,满足.
(1)填空:______,________;
(2)若存在一点,点M到x轴距离_______,到y轴距离_______,求的面积(用含m的式子表示);
(3)在(2)条件下,当时,在y轴上有一点P,使得的面积与的面积相等,请求出点P的坐标.
【变式2】
(2022秋·北京海淀·八年级北京育英中学校考期末)
9.如图,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)若线段与轴交于点,在轴上是否存在点,使得三角形和三角形的面积相等,若存在,求出点坐标;若不存在,请说明理由;
类型四、平面直角坐标系 判断点的位置 参数
(2022秋·江苏南京·八年级校考阶段练习)
10.如图,在平面直角坐标系中,A、B、C三点的坐标分别为.
(1)画出;
(2)面积为 ___________;
(3)如图,是由经过平移得到的.已知点为内的一点,则点P在内的对应点的坐标是 ___________.
举一反三:
【变式1】
(2022春·福建厦门·七年级统考期末)
11.在平面直角坐标系中,O为原点,点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
(1)求b和k的值;(用含a的代数式表示k)
(2)探求当a变化时,三角形与三角形的面积大小关系.
【变式2】
(2022秋·八年级课时练习)
12.在直角坐标系中,已知线段,点A的坐标为,点B的坐标为,如图1所示.
(1)平移线段到线段,使点A的对应点为D,点B的对应点为C,若点C的坐标为,求点D的坐标;
(2)平移线段到线段,使点C在y轴的正半轴上,点D在第二象限内,连接,,如图2所示.若(表示三角形的面积),求点C、D的坐标.
(3)在(2)的条件下,在y轴上是否存在一点P,使(表示三角形的面积)?若存在,求出点P的坐标;若不存在,请说明理由.
类型五、平面直角坐标系 图形的变换 对称问题
(2021秋·河北邢台·八年级统考期末)
13.如图,直角坐标系中,在边长为的正方形网格中,的顶点均在格点上,点,的坐标分别是,.
(1)请在图中画出关于轴的对称,点的坐标为______,点的坐标为______ ;
(2)请写出点关于轴的对称点的坐标为______;
(3)求的面积.
举一反三:
【变式1】
(2023秋·山东烟台·七年级统考期末)
14.如图,在直角坐标系中,的位置如图所示,请完成下列问题:
(1)分别写出点A,点C的坐标;
(2)作出关于x轴的对称图形,并写出的坐标为 .
(3)求的面积;
(4)在y轴上找一点P,使最小.
【变式2】
(2022秋·河北邯郸·八年级统考期中)
15.在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形(三角形的三个顶点都在小正方形上)
(1)画出关于直线:的对称三角形;并写出,,的坐标;
(2)在直线上找一点,使最小,满足条件的点为______.提示:直线是过点且垂直于轴的直线.
类型六、平面直角坐标系 中考真题
(2022·陕西·统考中考真题)
16.如图,的顶点坐标分别为.将平移后得到,且点A的对应点是,点B、C的对应点分别是.
(1)点A、之间的距离是__________;
(2)请在图中画出.
举一反三:
【变式1】
(2019·广西·统考中考真题)
17.如图,在平面直角坐标系中,已知的三个顶点坐标分别是
(1)将向上平移4个单位长度得到,请画出;
(2)请画出与关于轴对称的;
(3)请写出的坐标.
【变式2】
(2015·广西崇左·中考真题)
18.如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1),,
(2)路线见解析,走路线为
【分析】(1)结合图示,确定原点,再根据题意求出点的位置;
(2)结合图示,确定原点,再根据题意求出马走的路线.
【详解】(1)解:∵“帅”位于点(0,0),“相”位于点(4,2),
∴“马”所在的点的坐标为(-3,0),
点C的坐标为(1,3),
点D的坐标为(3,1).
故答案为,,.
(2)解:以 “帅”为(0,0),则“马”走的路线为,
如图:
.
【点睛】本题考查了用有序数对解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置.
2.(1)+3,+4,D,﹣2
(2)见解析
(3)10
【分析】(1)根据规定及实例可知A→C记为(3,4),C→D记为(1,﹣2);
(2)按题目所示平移规律分别向右向上平移2个格点,再向右平移2个格点,向下平移1个格点;向左平移2个格点,向上平移3个格点;向左平移1个向下平移两个格点即可得到点P的坐标,在图中标出即可.
(3)根据点的运动路径,表示出运动的距离,相加即可得到行走的总路径长.
【详解】(1)解:(1)∵规定:向上向右走为正,向下向左走为负,
∴A→C记为(+3,+4),C→D记为(+1,﹣2).
故答案为:+3,+4,D,﹣2;
(2)P点位置如图所示.
(3)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2).
则该甲虫走过的路线长为1+4+2+1+2=10.
【点睛】本题主要考查了利用坐标确定点的位置的方法,解题的关键是正确的理解从一个点到另一个点移动时,如何用坐标表示.
3.(1)学校在小明家北偏东45°方向2km处,博物馆在小明家南偏东50°方向4 km处
(2)图中到小明家距离相同的是学校和公园和影院
(3)见解析
【分析】(1)由图可知,学校在小明家北偏东45°方向2km处,博物馆在小明家南偏东50方向4km处;
(2)观察图形,根据OA, OE, OD的长度及图中各角度,即可得出结论.
(3)作北偏西60°角,取OE = 2即可.
【详解】(1)解:学校在小明家北偏东45°方向2km处,博物馆在小明家南偏东50°方向4 km处;
(2)图中到小明家距离相同的是学校和公园和影院;
(3)如图,点F即为小强家.
【点睛】本题考查了方向角,解题的关键是熟练掌握运用方位角及确定位置需要两个元素.
4.(1)7
(2)
(3)
【分析】(1)根据得点P的坐标为,即可得到点P到x轴的距离;
(2)列得,求出a即可;
(3)根据直线轴,得到,求出a即可.
【详解】(1)解:当时,点P的坐标为,
∴点P到x轴的距离为7;
(2),
解得,
∴点P的坐标为;
(3)∵直线轴,
∴,
解得,
∴点P的坐标为.
【点睛】此题考查了点到坐标轴的距离,平行于坐标轴的点的坐标特点,解一元一次方程,正确理解坐标与图形的关系是解题的关键.
5.(1);
(2).
【分析】(1)根据y轴上的点的横坐标等于零,可得,即可求出m的值,进而得到答案;
(2) 根据点Q到两坐标的距离相等,可得关于m的方程,解方程即可得出答案.
【详解】(1)解:点Q在y轴上,则,
解得,
所以;
故Q点的坐标为 ;
(2)解:当点Q在(即第一象限)角平分线上,即:,
解得:,
所以,
故Q点的坐标为:.
【点睛】本题考查了点的坐标,y轴上的点的横坐标等于零,在角平分线上点到两坐标轴距离相等.
6.(1)见解析
(2)18
(3)(0,-3)或(0,9)
【分析】(1)根据点的坐标直接确定出点A、B、C的位置即可;
(2)根据三角形的面积求解可得;
(3)设P(0,m),利用三角形ABP的面积与三角形ABC的面积相等,求出m值,进而得出答案.
【详解】(1)解:如图所示,
(2)解:∵A(-2,3),,,
,点到AB的距离是;
的面积是:;
(3)解: ∵A(-2,3),,
∴ABx轴,
设P(0,m),
∵点在轴上,且三角形的面积与三角形的面积相等,
∴,
解得:m=-3或m=9,
∴点的坐标为:(0,-3)或(0,9).
【点睛】本题考查坐标与图形性质,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答.
7.(1)
(2)或,
(3)的值是定值,,理由见解析
【分析】(1)根据绝对值和平方的非负性,即可进行解答;
(2)先根据A、B、C的坐标求出求出的值,再根据y轴上点的坐标特征,设,最后根据三角形的面积公式将表示出来即可;
(3)根据,得出,,再根据平分得出,进而得出,最后根据平行线的性质得出即可得出结论.
【详解】(1)解:∵,
∴,则,
∴;
(2)由(1)可知,
∴,
∵,
∴点C到x轴距离为2,
∴,
∵当M在y轴上时,
∴设,
∴,
∵,
∴,
∴,
∴或,
(3)如图2中,结论:的值是定值,
理由:∵,
∴,
∴,,
∵平分,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
【点睛】本题主要考查了非负数的性质,坐标与图形,平行线的性质,角平分线的定义,解题的关键是掌握相关知识点并灵活运用.
8.(1),3
(2),2,
(3)或
【分析】(1)可将变形为,再根据平方和绝对值的非负性即可求出a和b的值;
(2)由M点坐标即可直接得出点M到x轴距离为,到y轴距离为.又可求出,即可利用三角形面积公式求出;
(3)将代入,得.设,则.即得出,解出t的值,即得出点P的坐标.
【详解】(1)∵,
∴,
∴,解得:.
故答案为:,3;
(2)∵,
∴点M到x轴距离为,到y轴距离为.
由(1)可知,,
∴,
∴.
故答案为:,2,;
(3)当时,.
设,
∴.
∵,
∴,
解得:,
∴或.
【点睛】本题考查非负数的性质,点到坐标轴的距离,坐标与图形.利用数形结合的思想是解题关键.
9.(1)36
(2)或
【分析】(1)先根据非负数的性质求出,的值,进而得出,两点的坐标,根据三角形的面积公式即可得出结论;
(2)设,利用三角形和三角形的面积相等可得到关于的方程,再解方程求出即可得点坐标.
【详解】(1),
,,
解得,,
,,
轴,
,
,,
;
(2)设,
,
,
三角形和三角形的面积相等,,
,
,即,
解得:或,
或;
【点睛】本题昰三角形综合题,考查了非负数的性质、坐标与图形性质以及三角形面积公式,理解坐标与长度的关系是解题的关键.
10.(1)见解析
(2)8
(3)
【分析】(1)根据题意,画出,即可求解;
(2)用所在的长方形的面积减去其周围的三个三角形的面积,即可求解;
(3)根据题意得:是由先向右平移4个单位,再向下平移3个单位得到的,即可求解.
【详解】(1)解:如图,即为所求;
(2)解:的面积;
故答案为:8;
(3)解:根据题意得:是由先向右平移4个单位,再向下平移3个单位得到的,
∴点P在内的对应点的坐标是.
故答案为:
【点睛】本题主要考查了坐标与图形,图形变换,熟练掌握图形平移的性质是解题的关键.
11.(1);;
(2)
【分析】(1)由,,结合,可得线段向上平移,再根据点的平移规则列方程即可;
(2)由平移的性质可得:,,如图,可得,过作于,过作于,显然,,从而可得答案.
【详解】(1)解:如图,∵点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
∴,,
∴,即,解得:,
∴,,,
∴,
解得:;
(2)由平移的性质可得:,,如图,
∴,
过作于,过作于,
显然,
∴,
∴,
∴.
【点睛】本题考查的是平移的性质,点的平移的坐标变化规律,平移的性质,平行线的性质,熟练地利用平移的性质解题是关键.
12.(1);
(2),;
(3)存在点P,其坐标为或.
【分析】(1)利用平移的性质确定出平移的方向和距离,进而可得点D的坐标;
(2)设D点纵坐标为y,由平移的性质可得,,然后根据建立方程求出y的值即可;
(3)设出点P的坐标,表示出,然后根据建立方程求解即可.
【详解】(1)解:∵平移后的对应点为,
∴点B向左平移了5个单位长度,向上平移了4个单位长度,
∴A点平移后的对应点;
(2)解:设D点纵坐标为y,
∵点C在y轴上,点D在第二象限,
∴线段向左平移3个单位长度,向上平移个单位长度,
∴,,
连接,
则,
即
解得:,
∴,;
(3)解:设点,
∴,
∵,
∴,
∴,
∴或,
∴存在点P,其坐标为或.
【点睛】此题是几何变换综合题,主要考查了平移的性质,坐标与图形性质,解本题的关键是平移性质的灵活运用,用面积关系建立方程.
13.(1);;
(2)
(3)
【分析】(1)根据网格结构找出点、的位置,然后与点顺次连接即可,再根据平面直角坐标系写出点、的坐标;
(2)根据关于轴对称的点的横坐标相同,纵坐标互为相反数写出即可;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
【详解】(1)解:如图所示;点,;
故答案为:;;
(2)由图象可知:;
故答案为:.
(3),
,
.
【点睛】本题考查了利用轴对称变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.
14.(1),
(2)作图见解析,
(3)3.5
(4)作图见解析
【分析】(1)根据点的坐标的表示方法求解;
(2)利用关于y轴对称的点的坐标特征得到的坐标,然后描点连线即可;
(3)用一个矩形的面积分别减去三个直角三角形的面积去计算的面积;
(4)作点B关于x轴的对称点,连接交x轴于P点,利用两点之间线段最短可判断P点满足条件.
【详解】(1)解:由图形可知:;
(2)如下图,作点A、B、C关于y轴对称的点的坐标特征得到,连接即为所求;
(3)由题意可知:的面积;
(4)如(2)图,作点B关于x轴的对称点,连接交x轴于P点,
两点之间线段最短,
最小,
点P即为所求.
【点睛】本题考查了利用轴对称变换作图,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.
15.(1)图见解析,,,
(2)图见解析,点的坐标为
【分析】(1)分别作出点,,关于直线:的对称的点,然后顺次连接,并写出,,的坐标;
(2)作出点关于对称的点,连接,与的交点即为点,此时最小,写出点的坐标即可.
【详解】(1)解:如图,分别作出点,,关于直线:的对称的点,,,
连接,,,
则即为所作,
∴,,.
(2)如图,作点关于直线对称的点,连接,与直线的交点即为点,
∴直线为线段的垂直平分线,
∴,
∴,
∴此时最小,点坐标为.
故答案为:.
【点睛】本题考查根据轴对称变换作图,最短路线问题.解答本题的关键是根据网格结构作出对应点的位置并顺次连接.
16.(1)4
(2)见解析
【分析】(1)由得,A、之间的距离是2-(-2)=4;
(2)根据题意找出平移规律,求出,进而画图即可.
【详解】(1)解:由得,
A、之间的距离是2-(-2)=4.
故答案为:4.
(2)解:由题意,得,
如图,即为所求.
【点睛】本题考查了坐标系中两点之间的距离求解以及平移求点坐标画图,题目相对较简单,掌握平移规律是解决问题的关键.
17.(1)如图所示:,即为所求;见解析;(2)如图所示:,即为所求;见解析;(3).
【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用轴对称的性质得出对应点位置进而得出答案;
(3)利用所画图象得出对应点坐标.
【详解】(1)如图所示:,即为所求;
(2)如图所示:,即为所求;
(3).
【点睛】此题主要考查了轴对称变换以及平移变换,正确得出对应点位置是解题关键.
18.(1)作图见试题解析,A(-3,1), B(0,2),C(-1,4);(2)2.
【分析】(1)△A1B1C1是由△ABC向右平移4个单位得到的,故将△A1B1C1向左平移4个单位既是△ABC;
(2)由平移性质知,A1A平行于x轴,且等于平移距离4,△A1OA边A1OA上的高可点A1的坐标确定.
【详解】解:(1)A(-3,1), B(0,2),C(-1,4),如图:
(2)A1A=4,
∴=A1A×1=×4×1=2.
答案第1页,共2页
答案第1页,共2页
