专题7.4平面直角坐标系中的图形变化及其应用 知识讲解(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题7.4平面直角坐标系中的图形变化及其应用 知识讲解(含解析)2023-2024学年七年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 21:29:31 | ||
图片预览




文档简介
专题7.4 平面直角坐标系中的图形变化及其应用(知识讲解)
【学习目标】
1.能建立适当的平面直角坐标系描述物体的位置.
2.在同一直角坐标系中,掌握点和图形的平移规律,并用于解决问题;
3.在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系;
4.经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识;
5.通过“坐标与轴对称”的探究,让学生掌握空间与图形的基础知识和基本技能,培养学生的探索能力.
【要点梳理】
【知识点一】用坐标表示地理位置
根据已知条件,建立适当的平面直角坐标系,是确定点的位置的必经过程,只有建立了适当的直角坐标系,点的位置才能得以确定,才能使数与形有机地结合在一起.
利用平面直角坐标系绘制区域内一些地点分布情况的过程:
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴,y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
特别说明:
(1)建立坐标系的关键是确定原点和坐标轴的位置,我们一般选择那些使点的位置比较容易确定的方法,例如借助于图形的某边所在直线为坐标轴等,而建立平面直角坐标系的方法是不唯一的.所建立的平面直角坐标系也不同,得到的点的坐标不同.
(2)应注意比例尺和坐标轴上的单位长度的确定.
【知识点二】平面直角坐标系中点和图形的平移
(1)点在平面直角坐标系中的平移
在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或 (x-a,y);将点(x,y)向上或向下平移b单位长度,可以得到对应点((x,y+b)或((x,y-b).
特别说明:
(1)、在坐标系内,左右平移的点的坐标规律:右加左减;
(2)、在坐标系内,上下平移的点的坐标规律:上加下减;
(3)、在坐标系内,平移点的坐标规律:沿x轴方向平移纵坐标不变,沿y轴方向平移横坐标不变.
(2)图形在平面直角坐标系中的平移
在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度:如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
特别说明:
(1) 平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决;
(2) 平移只改变图形的位置,图形的大小和形状不发生变化.
【知识点三】轴对称定理
定理1:关于某条直线对称的两个图形是全等形.(全等形不一定关于某条直线对称)
定理2:如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线.
定理3:两个图形关于某条直线对称,如果对称轴和某两条对称线段的延长线相交,那么交点在对称轴上.
定理3的逆定理:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
【知识点四】平面直角坐标系中对称点坐标
P(a,b)关于x轴对称的点的坐标为 (a,-b);
P(a,b)关于y轴对称的点的坐标为 (-a,b);
P(a,b)关于原点对称的点的坐标为 (-a,-b);
P(a,b)关于一三象限角平分线对称的点的坐标为 (b,a);
P(a,b)关于一三象限角平分线对称的点的坐标为 (-b,-a).
【典型例题】
类型一、用坐标表示平移 平移方式(点的坐标) 点的坐标(平移方式)
1.在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
举一反三:
【变式1】
2.在平面直角坐标系中,将点A(m﹣1,n+2)先向右平移3个单位,再向上平移2个单位,得到点.若点位于第四象限,则m、n的取值范围分别是( )
A.m>0,n<0 B.m>1,n<2 C.m>1,n<0 D.m>﹣2,n<﹣4
【变式2】
3.如图第一象限内有两点,将线段平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是( ).
A. B. C.或 D.或
4.如图,在平面直角坐标系中,将四边形先向上平移,再向左平移得到四边形,已知,则点B坐标为( )
A. B. C. D.
举一反三:
【变式1】
5.在平面直角坐标系中,线段A'B'是由线段AB经过平移得到的,已知点A(2,1)的对应点为A'(3,1),点B的对应点为B'(4,0),则点B的坐标为( )
A.(9,2) B.(1,2) C.(1,3) D.( 1,2)
【变式2】
6.若将点A先向左平移1个单位,再向上平移4个单位,得到的B(-3,2),则点A的坐标为( )
A.(-1,6) B.(-4,6) C.(-2,-2) D.(-4,-2)
类型二、平面直角坐标系 有序对 表示位置 表示路线
7.某体育馆的平面示意图如图所示,已知游泳馆的坐标是,足球场的坐标是.
(1)根据上述条件建立平面直角坐标系;
(2)若篮球场的坐标为,请在图中标出篮球场的位置.
举一反三:
【变式1】
8.如图是某学校平面图的一部分,若宿舍楼的坐标为,致远楼的坐标为,请解答下列问题:
(1)根据题目信息,建立平面直角坐标系;
(2)根据你建立的平面直角坐标系,写出教务处的坐标;
(3)若图书馆的坐标为,请在图中标出图书馆的位置.
【变式2】
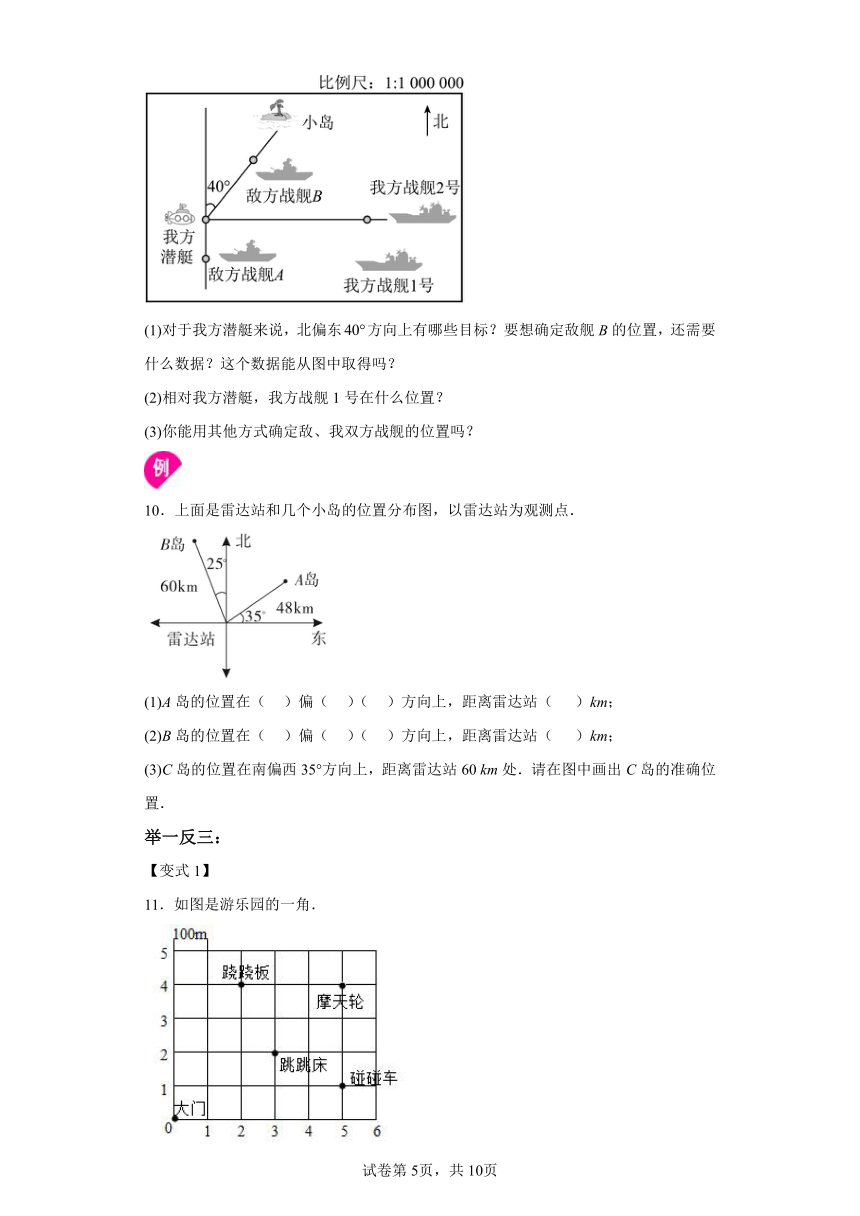
9.如图为某次军事演习敌我双方舰艇模拟对峙图.
(1)对于我方潜艇来说,北偏东方向上有哪些目标?要想确定敌舰B的位置,还需要什么数据?这个数据能从图中取得吗?
(2)相对我方潜艇,我方战舰1号在什么位置?
(3)你能用其他方式确定敌、我双方战舰的位置吗?
10.上面是雷达站和几个小岛的位置分布图,以雷达站为观测点.
(1)A岛的位置在( )偏( )( )方向上,距离雷达站( )km;
(2)B岛的位置在( )偏( )( )方向上,距离雷达站( )km;
(3)C岛的位置在南偏西35°方向上,距离雷达站60 km处.请在图中画出C岛的准确位置.
举一反三:
【变式1】
11.如图是游乐园的一角.
(1)如果用(3,2)表示跳跳床的位置,那么跷跷板用数对________表示,碰碰车用数对________表示,摩天轮用数对________表示.
(2)请你在图中标出秋千的位置,秋千在大门以东400m,再往北300m处.
【变式2】
12.在一次夏令营活动中,主办方告诉营员们A、B两点的位置及坐标分别为(-3,1)、(-2,-3),同时只告诉营员们活动中心C的坐标为(3,2)(单位:km)
(1)请在图中建立直角坐标系并确定点C的位置;
(2)以点B为参照点,请用方位角和实际距离表示点C的位置.
类型三、平面直角坐标系 轴对称 点的坐标 面积 最值
13.如图,已知的顶点分别为,,和直线m(直线m上各点的横坐标都为1).
(1)作出关于x轴对称的图形,并写出点的坐标;
(2)若点是内部一点,则点P关于直线m对称的点的坐标是______.
(3)在x轴上找一点P,使得最小,找到点P的位置.
举一反三:
【变式1】
14.如图,已知的三个顶点坐标分别为,,.
(1)画出关于轴对称的图形;
(2)直接写出、的坐标为____________;
(3)求的面积.
【变式2】
15.如图,三个顶点的坐标分别是,,.
(1)若点A、B、C关于x轴的对称点分别为、、,则(____,____),(____,____,)(____,____),并在图中画出.
(2)求的面积;
(3)在x轴上求一点P,使周长最小,请画出,并通过画图求出P点的坐标.
类型四、平面直角坐标系 轴对称 平移 综合题(几何图形变换)
16.小亮在网上搜索到下面的文字材料:在x轴上有两个点它们的坐标分别为和.则这两个点所成的线段的长为;同样,若在轴上的两点坐标分别为和,则这两个点所成的线段的长为.如图1,在直角坐标系中的任意两点,其坐标分别为和,分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边,利用勾股定理可得:线段的长为.
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知则线段的长为______;
(2)若点在y轴上,点的坐标是,且,则点的坐标是______;
(3)如图2,在直角坐标系中,点的坐标分别为)和,点是轴上的一个动点,且三点不在同一条直线上,求周长的最小值.
举一反三:
【变式1】
17.在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形(三角形的三个顶点都在小正方形上)
(1)画出关于直线:的对称三角形;并写出,,的坐标;
(2)在直线上找一点,使最小,满足条件的点为______.提示:直线是过点且垂直于轴的直线.
【变式2】
18.如图,在平面直角坐标系中,点的坐标分别为和,是轴上的一个动点,且三点不在同一条直线上.
(1)求的长;
(2)求的周长的最小值.
19.如图,平面直角坐标系中,,,,,.
(1)求的面积;
(2)如图,点以每秒个单位的速度向下运动至,与此同时,点从原点出发,以每秒个单位的速度沿轴向右运动至,秒后,、、在同一直线上,求的值;
(3)如图,点在线段上,将点向右平移个单位长度至点,若的面积等于,求点坐标.
举一反三:
【变式1】
20.在平面直角坐标系中,点,的坐标分别为,,现将线段先向上平移3个单位,再向右平移1个单位,得到线段,连接,.
(1)如图1,求点,的坐标及四边形的面积;
(2)如图1,在轴上是否存在点,连接,,使?若存在这样的点,求出点的坐标;若不存在,试说明理由;
(3)如图2,点为与轴交点,在直线上是否存在点,连接,使?若存在这样的点,直接写出点的坐标;若不存在,试说明理由;
【变式2】
21.在平面直角坐标系中,,,a,b满足,连接AB交y轴于C.
(1)直接写出______,______;
(2)如图1,点P是y轴上一点,且三角形ABP的面积为12,求点P的坐标;
(3)如图2,直线BD交x轴于,将直线BD平移经过点A,交y轴于E,点在直线AE上,且三角形ABQ的面积不超过三角形ABD面积的,求点Q横坐标x的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
【详解】解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点睛】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
2.D
【分析】先根据平移得到点的坐标,再根据点在第四象限构建不等式解决问题.
【详解】解:由题意,点的坐标为(,),
即:(,),
∵点位于第四象限,
∴,
∴,
故选:D.
【点睛】本题考查坐标与图形变化-平移,解题的关键是构建不等式解决问题,属于中考常考题型.
3.C
【分析】设平移后点、的对应点分别是、.分两种情况进行讨论:①在轴上,在轴上;②在轴上,在轴上.
【详解】解:设平移后点、的对应点分别是、.
分两种情况:
①在轴上,在轴上,
则横坐标为0,纵坐标为0,
,
,
点平移后的对应点的坐标是;
②在轴上,在轴上,
则纵坐标为0,横坐标为0,
,
,
点平移后的对应点的坐标是;
综上可知,点平移后的对应点的坐标是或.
故选:C.
【点睛】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
4.B
【解析】由题意得到点A的坐标变化规律,然后根据点A的变化规律反推可以由B1得到B的坐标.
【详解】解:∵-3-3=-6,5-3=2,
∴点A变到A1的过程中,横坐标加-6,纵坐标加2,
∴由B1反推到B的过程,必须是横坐标加6,纵坐标加-2,
∴-4+6=2,3-2=1,
∴B点坐标为(2,1),
故选B.
【点睛】本题考查平移的坐标变化,得到图形的平移规律是解题关键.
5.D
【分析】直接利用平移中点的变化规律求解即可.
【详解】横坐标从-2到3,说明是向右移动了3-(-2)=5,纵坐标从1到-1,说明是向下移动了1-(-1)=2,
求原来点的坐标,则为让新坐标的横坐标都减5,纵坐标都加2.
则点B的坐标为(-1,2).
故答案为:D.
【点睛】本题考查了图形的平移变换,注意左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.求原来点的坐标正好相反.
6.C
【详解】试题解析:设A(x,y),将点A先向左平移1个单位,再向上平移4个单位可得(x-1,y+4),
∵得到的B(-3,2),
∴x-1=-3,y+4=2,
解得:x=-2,y=-2,
∴A(-2,-2),
故选C.
【点睛】此题主要考查了平移变换与坐标变化,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.
7.(1)见解析
(2)见解析
【分析】(1)根据数对表示的位置,即可建立出平面直角坐标系.
(2)根据数对表示的位置,第一个数字表示列,第二个数字表示行,即可标出篮球场的位置.
【详解】(1)建立平面直角坐标系如图所示.
(2)篮球场的位置如图所示.
【点睛】本题考查了坐标方法的简单应用以及数对表示位置的方法,正确建立平面直角坐标系是解题的关键.
8.(1)见解析
(2)
(3)见解析
【分析】(1)根据宿舍楼和致远楼的坐标,确定出原点以及坐标轴,即可求解;
(2)根据直角坐标系以及教务处的位置,即可求解;
(3)根据图书馆的坐标,在坐标系中标记即可.
【详解】(1)建立平面直角坐标系如图所示.
(2)教务处的坐标为.
(3)图书馆的位置如图所示.
【点睛】此题考查了直角坐标系的应用,坐标确定位置,根据题意正确得到原点的位置以及坐标轴是解题的关键.
9.(1)敌方战舰,小岛,潜艇到敌方战舰的距离,能从图中取得,理由见解析;
(2)相对我方潜艇,我方战舰1是在东偏南的位置;
(3)建立坐标系,利用有序数对来表示.
【分析】(1)根据方向角的定义即可得到结论;
(2)根据方向角来表示,即可得到结论;
(3)根据方向角的定义即可得到结论.
【详解】(1)解:北偏东方向上的目标是敌方战舰,小岛.
要确定敌方战舰的位置,还需要潜艇到敌方战舰的距离,
这个数据能从图中取得,测量潜艇到敌方战舰的图上距离,再按的比例求解;
(2)解:相对我方潜艇,我方战舰1是在东偏南的位置;
(3)解:可以建立坐标系,利用有序数对来表示,即坐标来表示敌、我双方战舰的位置.
【点睛】本题考查了方向角,平面直角坐标系,解题的关键是熟练掌握方向角的定义.
10.(1)北偏东、55°、48
(2)北偏西、25°、60
(3)见解析
【分析】(1)根据地图上的方向,上北下南,左西右东,以雷达站的位置为观测点,即可确定A岛位置的方向,距离图中已标出.
(2)同理,以雷达站的位置为观测点,即可确定B岛位置的方向,距离图中已标出.
(3)C岛到雷达站的实际距离与B岛到雷达站的实际距离相等,因此,图上距离也相等,以雷达站为观测点,即可确定C岛的方向,由此即可画出C岛的准确位置.
【详解】(1)A岛的位置在北偏东55°方向上,距离雷达站48km;
(2)B岛的位置在北偏西25°方向上,距离雷达站60km;
(3)C岛的位置在南偏西35°方向上,距离雷达站60km处.
在图中画出C岛的准确位置(下图):
【点睛】本题考查根据方向和距离确定物体的位置,会根据位置描述方向以及会根据方向的描述确定物体的位置是解本题的关键.
11.(1)(2,4);(5,1);(5,4);(2)见解析.
【分析】(1)根据有序数对的定义分别写出即可;
(2)根据网格结构找出秋千的位置标注即可.
【详解】解:(1)(2,4);(5,1);(5,4);
(2)如图.
【点睛】本题考查坐标确定位置.
12.(1)见解析;
(2)点C在点B东北方向,距离点B的km处
【分析】(1)根据题意建立直角坐标系,再由坐标系写出点C的坐标即可;
(2)以点B为坐标中心,由方向角的定义可知点C在点B北偏东45°方向上,再由勾股定理求出BC的长.
【详解】(1)解:根据A(-3,1),B(-2,-3)画出直角坐标系,
描出点C(3,2),如图所示:
(2)由勾股定理可知,BC=5,
∴点C在点B北偏东45°方向上,距离点B的5km处.
【点睛】本题考查直角坐标系,用坐标系中的点表示位置、方向角、勾股定理等知识,是基础考点,掌握相关知识是解题关键.
13.(1),图见解析
(2)
(3)图见解析
【分析】(1)根据轴对称关系确定点、、的坐标,顺次连线即可;
(2)根据轴对称的性质解答即可;
(3)连接,与x轴交点即为点P.
【详解】(1)解:如下图所示.点的坐标为;
(2)解:直线m上各点的横坐标都为1,
,
由轴对称的性质可知,点关于直线m对称的点的横坐标为,纵坐标为b,
即点关于直线m对称的点的坐标为,
故答案为:;
(3)解:如图,连接,与x轴交点即为点P.
理由如下:
点C和点关于x轴对称,
,
,
即此时最小.
【点睛】本题考查轴对称的性质,利用轴对称关系作图,确定直角坐标系中点的坐标,最短路径问题作图,正确理解轴对称的性质是解题的关键.
14.(1)见解析
(2)的坐标为、的坐标为
(3)2
【分析】(1)根据轴对称的定义找到的三个顶点关于轴对称的点,再顺次连接即可;
(2)根据所作图形可得;
(3)利用割补法求解即可.
【详解】(1)解:如图所示,即为所求;
(2)由图象知的坐标为、的坐标为;
(3)的面积:.
【点睛】本题考查了轴对称变换,正确得出对应点位置是解题的关键.
15.(1),,,画图见解析;
(2)
(3)画图见解析,
【分析】(1)根据关于x轴对称的点的坐标特点可得、、的坐标,再顺次连接、、作三角形即可;
(2)由长方形的面积减去周围三个三角形的面积即可;
(3)如图,连接交x轴于点P,则的周长最小,再根据图形可得P的坐标.
【详解】(1)解:∵,,.
∴点A、B、C关于x轴的对称点、、的坐标为:
,,,
如图,即为所画的三角形,
(2).
(3)如图,连接交x轴于点P,
则,
∴,
此时的周长最小.
由作图可得:.
【点睛】本题考查的是画关于x轴对称的三角形,坐标与图形,求网格中三角形的面积,利用轴对称的性质确定三角形周长最小时点的位置与坐标,熟练的运用轴对称的性质进行解题是关键.
16.(1)
(2)或
(3)周长最小值为
【分析】(1)根据勾股定理直接进行计算即可求解;
(2)设,由点的坐标是,且,根据勾股定理建立方程,解方程即可求解.
(3)作点关于轴的对称点,根据对称性可得即为周长最小值,勾股定理求得即可求解.
【详解】(1)解:∵
∴,
故答案为:;
(2)设,∵点的坐标是,且,
∴,
解得,
∴点的坐标是:或,
故答案为:或;
(3)如图2,作点关于轴的对称点,则点,
∴,当三点共线时,最小,即周长最小,
∵,,,
,
,
∴△ABC周长最小值为:.
【点睛】本题考查了勾股定理求两点距离,轴对称的性质求线段和的最值问题,掌握勾股定理,轴对称的性质是解题的关键.
17.(1)图见解析,,,
(2)图见解析,点的坐标为
【分析】(1)分别作出点,,关于直线:的对称的点,然后顺次连接,并写出,,的坐标;
(2)作出点关于对称的点,连接,与的交点即为点,此时最小,写出点的坐标即可.
【详解】(1)解:如图,分别作出点,,关于直线:的对称的点,,,
连接,,,
则即为所作,
∴,,.
(2)如图,作点关于直线对称的点,连接,与直线的交点即为点,
∴直线为线段的垂直平分线,
∴,
∴,
∴此时最小,点坐标为.
故答案为:.
【点睛】本题考查根据轴对称变换作图,最短路线问题.解答本题的关键是根据网格结构作出对应点的位置并顺次连接.
18.(1)
(2)
【分析】(1)过点作于,则∠,,,,得出,由勾股定理求出即可;
(2)由题意得出最小,作关于y轴的对称点,连接交轴于点,点即为使最小的点,由勾股定理求出,即可求解;
【详解】(1)解:过点作于,如图,
则,
∵点的坐标分别为和,
∴,,,
∴,
∴;
(2)要使的周长最小,长度一定,
则最小,
作关于轴的对称点,连接交轴于点,过点作于点,如图,
∵,
∴当三点共线时,即与重合时,三角形的周长最小,最小值为的长,
由对称的性质得:,
∴
∴,
在中,,
∴,
∴的周长的最小值为.
【点睛】本题考查了勾股定理求两点距离,轴对称求线段和的最值问题,掌握轴对称的性质以及勾股定理是解题的关键.
19.(1)
(2)
(3)
【分析】(1)由非负数的性质求出,求出,由三点的坐标可求出答案;
(2)根据三角形的面积关系可得出答案;
(3)连接,设,由三角形面积关系得出,由平移的性质得出,根据三角形的面积关系可求出答案.
【详解】(1),,,
,,
,,
,
,,,
,,
;
(2)由题意知:,,
,
,
.
(3)连接,,
设,
,
,
,
点向右平移个单位长度得到点,
,
,
,
,
,
【点睛】本题是三角形综合题,考查了非负数的性质,坐标与图形的性质,平移的性质,三角形的面积等知识,解题的关键是学会利用参数构建方程解决问题.
20.(1)12;
(2)或;
(3)或.
【分析】(1)根据平移的性质求出点,的坐标,根据平行四边形的面积公式求出四边形的面积;
(2)根据三角形的面积公式计算即可;
(3)根据直线上点的坐标特征设出点的坐标,根据三角形的面积公式计算即可.
【详解】(1)解:(1)∵点,的坐标分别为,,线段先向上平移3个单位,再向右平移1个单位,得到线段,
∴点的坐标为,点的坐标为,,
∴四边形的面积;
(2)存在,
设点的坐标为,
由题意得:,
解得:,
∴点的坐标为或;
(3)设点的坐标为,
则,
由题意得:,
解得:或,
则点的坐标为或.
【点睛】本题考查的是平移的性质、三角形的面积计算、点的坐标特征,根据平移变换的性质求出点,的坐标是解题的关键.
21.(1)-3,4
(2)-3,4
(3)-4≤x≤-2且x≠-3
【分析】(1)根据非负数的性质构建方程组,解方程组求出,;
(2)过点作轴于,设,由三角形面积关系得出,求出,过点作轴于,由三角形面积关系得出,求出即可;
(3)连接,过点作轴,分点在第二象限,点在第三象限时,两种情况,分别列出方程,解之即可.
【详解】(1)解:,
又∵,,
,
解得:,
故答案为:-3,4.
(2)过点作轴于,
设,
三角形的面积四边形的面积三角形的面积,
,
即,
解得:,
点的坐标为,
过点作轴于,
三角形的面积三角形的面积三角形的面积,
,
即,
,
点的坐标为或.
(3)点向左平移4个单位长度,向下平移4个单位长度到点A,
∵点D向左平移4个单位长度后的对应点正好在y轴上,
∴点平移后的对应点恰好是点,
连接,过点作轴,如图所示:
,
三角形的面积三角形的面积,
当三角形的面积三角形的面积时,,
当点在第三象限时,
,
解得:,
当点在第二象限时,
,
解得:,
当三角形的面积不超过三角形面积的时,
点的横坐标的取值范围是,且.
【点睛】本题属于三角形综合题,考查了三角形的面积,非负数的性质,平行线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
答案第1页,共2页
答案第1页,共2页
【学习目标】
1.能建立适当的平面直角坐标系描述物体的位置.
2.在同一直角坐标系中,掌握点和图形的平移规律,并用于解决问题;
3.在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系;
4.经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识;
5.通过“坐标与轴对称”的探究,让学生掌握空间与图形的基础知识和基本技能,培养学生的探索能力.
【要点梳理】
【知识点一】用坐标表示地理位置
根据已知条件,建立适当的平面直角坐标系,是确定点的位置的必经过程,只有建立了适当的直角坐标系,点的位置才能得以确定,才能使数与形有机地结合在一起.
利用平面直角坐标系绘制区域内一些地点分布情况的过程:
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴,y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
特别说明:
(1)建立坐标系的关键是确定原点和坐标轴的位置,我们一般选择那些使点的位置比较容易确定的方法,例如借助于图形的某边所在直线为坐标轴等,而建立平面直角坐标系的方法是不唯一的.所建立的平面直角坐标系也不同,得到的点的坐标不同.
(2)应注意比例尺和坐标轴上的单位长度的确定.
【知识点二】平面直角坐标系中点和图形的平移
(1)点在平面直角坐标系中的平移
在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或 (x-a,y);将点(x,y)向上或向下平移b单位长度,可以得到对应点((x,y+b)或((x,y-b).
特别说明:
(1)、在坐标系内,左右平移的点的坐标规律:右加左减;
(2)、在坐标系内,上下平移的点的坐标规律:上加下减;
(3)、在坐标系内,平移点的坐标规律:沿x轴方向平移纵坐标不变,沿y轴方向平移横坐标不变.
(2)图形在平面直角坐标系中的平移
在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度:如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
特别说明:
(1) 平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决;
(2) 平移只改变图形的位置,图形的大小和形状不发生变化.
【知识点三】轴对称定理
定理1:关于某条直线对称的两个图形是全等形.(全等形不一定关于某条直线对称)
定理2:如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线.
定理3:两个图形关于某条直线对称,如果对称轴和某两条对称线段的延长线相交,那么交点在对称轴上.
定理3的逆定理:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
【知识点四】平面直角坐标系中对称点坐标
P(a,b)关于x轴对称的点的坐标为 (a,-b);
P(a,b)关于y轴对称的点的坐标为 (-a,b);
P(a,b)关于原点对称的点的坐标为 (-a,-b);
P(a,b)关于一三象限角平分线对称的点的坐标为 (b,a);
P(a,b)关于一三象限角平分线对称的点的坐标为 (-b,-a).
【典型例题】
类型一、用坐标表示平移 平移方式(点的坐标) 点的坐标(平移方式)
1.在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
举一反三:
【变式1】
2.在平面直角坐标系中,将点A(m﹣1,n+2)先向右平移3个单位,再向上平移2个单位,得到点.若点位于第四象限,则m、n的取值范围分别是( )
A.m>0,n<0 B.m>1,n<2 C.m>1,n<0 D.m>﹣2,n<﹣4
【变式2】
3.如图第一象限内有两点,将线段平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是( ).
A. B. C.或 D.或
4.如图,在平面直角坐标系中,将四边形先向上平移,再向左平移得到四边形,已知,则点B坐标为( )
A. B. C. D.
举一反三:
【变式1】
5.在平面直角坐标系中,线段A'B'是由线段AB经过平移得到的,已知点A(2,1)的对应点为A'(3,1),点B的对应点为B'(4,0),则点B的坐标为( )
A.(9,2) B.(1,2) C.(1,3) D.( 1,2)
【变式2】
6.若将点A先向左平移1个单位,再向上平移4个单位,得到的B(-3,2),则点A的坐标为( )
A.(-1,6) B.(-4,6) C.(-2,-2) D.(-4,-2)
类型二、平面直角坐标系 有序对 表示位置 表示路线
7.某体育馆的平面示意图如图所示,已知游泳馆的坐标是,足球场的坐标是.
(1)根据上述条件建立平面直角坐标系;
(2)若篮球场的坐标为,请在图中标出篮球场的位置.
举一反三:
【变式1】
8.如图是某学校平面图的一部分,若宿舍楼的坐标为,致远楼的坐标为,请解答下列问题:
(1)根据题目信息,建立平面直角坐标系;
(2)根据你建立的平面直角坐标系,写出教务处的坐标;
(3)若图书馆的坐标为,请在图中标出图书馆的位置.
【变式2】
9.如图为某次军事演习敌我双方舰艇模拟对峙图.
(1)对于我方潜艇来说,北偏东方向上有哪些目标?要想确定敌舰B的位置,还需要什么数据?这个数据能从图中取得吗?
(2)相对我方潜艇,我方战舰1号在什么位置?
(3)你能用其他方式确定敌、我双方战舰的位置吗?
10.上面是雷达站和几个小岛的位置分布图,以雷达站为观测点.
(1)A岛的位置在( )偏( )( )方向上,距离雷达站( )km;
(2)B岛的位置在( )偏( )( )方向上,距离雷达站( )km;
(3)C岛的位置在南偏西35°方向上,距离雷达站60 km处.请在图中画出C岛的准确位置.
举一反三:
【变式1】
11.如图是游乐园的一角.
(1)如果用(3,2)表示跳跳床的位置,那么跷跷板用数对________表示,碰碰车用数对________表示,摩天轮用数对________表示.
(2)请你在图中标出秋千的位置,秋千在大门以东400m,再往北300m处.
【变式2】
12.在一次夏令营活动中,主办方告诉营员们A、B两点的位置及坐标分别为(-3,1)、(-2,-3),同时只告诉营员们活动中心C的坐标为(3,2)(单位:km)
(1)请在图中建立直角坐标系并确定点C的位置;
(2)以点B为参照点,请用方位角和实际距离表示点C的位置.
类型三、平面直角坐标系 轴对称 点的坐标 面积 最值
13.如图,已知的顶点分别为,,和直线m(直线m上各点的横坐标都为1).
(1)作出关于x轴对称的图形,并写出点的坐标;
(2)若点是内部一点,则点P关于直线m对称的点的坐标是______.
(3)在x轴上找一点P,使得最小,找到点P的位置.
举一反三:
【变式1】
14.如图,已知的三个顶点坐标分别为,,.
(1)画出关于轴对称的图形;
(2)直接写出、的坐标为____________;
(3)求的面积.
【变式2】
15.如图,三个顶点的坐标分别是,,.
(1)若点A、B、C关于x轴的对称点分别为、、,则(____,____),(____,____,)(____,____),并在图中画出.
(2)求的面积;
(3)在x轴上求一点P,使周长最小,请画出,并通过画图求出P点的坐标.
类型四、平面直角坐标系 轴对称 平移 综合题(几何图形变换)
16.小亮在网上搜索到下面的文字材料:在x轴上有两个点它们的坐标分别为和.则这两个点所成的线段的长为;同样,若在轴上的两点坐标分别为和,则这两个点所成的线段的长为.如图1,在直角坐标系中的任意两点,其坐标分别为和,分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边,利用勾股定理可得:线段的长为.
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知则线段的长为______;
(2)若点在y轴上,点的坐标是,且,则点的坐标是______;
(3)如图2,在直角坐标系中,点的坐标分别为)和,点是轴上的一个动点,且三点不在同一条直线上,求周长的最小值.
举一反三:
【变式1】
17.在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形(三角形的三个顶点都在小正方形上)
(1)画出关于直线:的对称三角形;并写出,,的坐标;
(2)在直线上找一点,使最小,满足条件的点为______.提示:直线是过点且垂直于轴的直线.
【变式2】
18.如图,在平面直角坐标系中,点的坐标分别为和,是轴上的一个动点,且三点不在同一条直线上.
(1)求的长;
(2)求的周长的最小值.
19.如图,平面直角坐标系中,,,,,.
(1)求的面积;
(2)如图,点以每秒个单位的速度向下运动至,与此同时,点从原点出发,以每秒个单位的速度沿轴向右运动至,秒后,、、在同一直线上,求的值;
(3)如图,点在线段上,将点向右平移个单位长度至点,若的面积等于,求点坐标.
举一反三:
【变式1】
20.在平面直角坐标系中,点,的坐标分别为,,现将线段先向上平移3个单位,再向右平移1个单位,得到线段,连接,.
(1)如图1,求点,的坐标及四边形的面积;
(2)如图1,在轴上是否存在点,连接,,使?若存在这样的点,求出点的坐标;若不存在,试说明理由;
(3)如图2,点为与轴交点,在直线上是否存在点,连接,使?若存在这样的点,直接写出点的坐标;若不存在,试说明理由;
【变式2】
21.在平面直角坐标系中,,,a,b满足,连接AB交y轴于C.
(1)直接写出______,______;
(2)如图1,点P是y轴上一点,且三角形ABP的面积为12,求点P的坐标;
(3)如图2,直线BD交x轴于,将直线BD平移经过点A,交y轴于E,点在直线AE上,且三角形ABQ的面积不超过三角形ABD面积的,求点Q横坐标x的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
【详解】解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点睛】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
2.D
【分析】先根据平移得到点的坐标,再根据点在第四象限构建不等式解决问题.
【详解】解:由题意,点的坐标为(,),
即:(,),
∵点位于第四象限,
∴,
∴,
故选:D.
【点睛】本题考查坐标与图形变化-平移,解题的关键是构建不等式解决问题,属于中考常考题型.
3.C
【分析】设平移后点、的对应点分别是、.分两种情况进行讨论:①在轴上,在轴上;②在轴上,在轴上.
【详解】解:设平移后点、的对应点分别是、.
分两种情况:
①在轴上,在轴上,
则横坐标为0,纵坐标为0,
,
,
点平移后的对应点的坐标是;
②在轴上,在轴上,
则纵坐标为0,横坐标为0,
,
,
点平移后的对应点的坐标是;
综上可知,点平移后的对应点的坐标是或.
故选:C.
【点睛】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
4.B
【解析】由题意得到点A的坐标变化规律,然后根据点A的变化规律反推可以由B1得到B的坐标.
【详解】解:∵-3-3=-6,5-3=2,
∴点A变到A1的过程中,横坐标加-6,纵坐标加2,
∴由B1反推到B的过程,必须是横坐标加6,纵坐标加-2,
∴-4+6=2,3-2=1,
∴B点坐标为(2,1),
故选B.
【点睛】本题考查平移的坐标变化,得到图形的平移规律是解题关键.
5.D
【分析】直接利用平移中点的变化规律求解即可.
【详解】横坐标从-2到3,说明是向右移动了3-(-2)=5,纵坐标从1到-1,说明是向下移动了1-(-1)=2,
求原来点的坐标,则为让新坐标的横坐标都减5,纵坐标都加2.
则点B的坐标为(-1,2).
故答案为:D.
【点睛】本题考查了图形的平移变换,注意左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.求原来点的坐标正好相反.
6.C
【详解】试题解析:设A(x,y),将点A先向左平移1个单位,再向上平移4个单位可得(x-1,y+4),
∵得到的B(-3,2),
∴x-1=-3,y+4=2,
解得:x=-2,y=-2,
∴A(-2,-2),
故选C.
【点睛】此题主要考查了平移变换与坐标变化,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.
7.(1)见解析
(2)见解析
【分析】(1)根据数对表示的位置,即可建立出平面直角坐标系.
(2)根据数对表示的位置,第一个数字表示列,第二个数字表示行,即可标出篮球场的位置.
【详解】(1)建立平面直角坐标系如图所示.
(2)篮球场的位置如图所示.
【点睛】本题考查了坐标方法的简单应用以及数对表示位置的方法,正确建立平面直角坐标系是解题的关键.
8.(1)见解析
(2)
(3)见解析
【分析】(1)根据宿舍楼和致远楼的坐标,确定出原点以及坐标轴,即可求解;
(2)根据直角坐标系以及教务处的位置,即可求解;
(3)根据图书馆的坐标,在坐标系中标记即可.
【详解】(1)建立平面直角坐标系如图所示.
(2)教务处的坐标为.
(3)图书馆的位置如图所示.
【点睛】此题考查了直角坐标系的应用,坐标确定位置,根据题意正确得到原点的位置以及坐标轴是解题的关键.
9.(1)敌方战舰,小岛,潜艇到敌方战舰的距离,能从图中取得,理由见解析;
(2)相对我方潜艇,我方战舰1是在东偏南的位置;
(3)建立坐标系,利用有序数对来表示.
【分析】(1)根据方向角的定义即可得到结论;
(2)根据方向角来表示,即可得到结论;
(3)根据方向角的定义即可得到结论.
【详解】(1)解:北偏东方向上的目标是敌方战舰,小岛.
要确定敌方战舰的位置,还需要潜艇到敌方战舰的距离,
这个数据能从图中取得,测量潜艇到敌方战舰的图上距离,再按的比例求解;
(2)解:相对我方潜艇,我方战舰1是在东偏南的位置;
(3)解:可以建立坐标系,利用有序数对来表示,即坐标来表示敌、我双方战舰的位置.
【点睛】本题考查了方向角,平面直角坐标系,解题的关键是熟练掌握方向角的定义.
10.(1)北偏东、55°、48
(2)北偏西、25°、60
(3)见解析
【分析】(1)根据地图上的方向,上北下南,左西右东,以雷达站的位置为观测点,即可确定A岛位置的方向,距离图中已标出.
(2)同理,以雷达站的位置为观测点,即可确定B岛位置的方向,距离图中已标出.
(3)C岛到雷达站的实际距离与B岛到雷达站的实际距离相等,因此,图上距离也相等,以雷达站为观测点,即可确定C岛的方向,由此即可画出C岛的准确位置.
【详解】(1)A岛的位置在北偏东55°方向上,距离雷达站48km;
(2)B岛的位置在北偏西25°方向上,距离雷达站60km;
(3)C岛的位置在南偏西35°方向上,距离雷达站60km处.
在图中画出C岛的准确位置(下图):
【点睛】本题考查根据方向和距离确定物体的位置,会根据位置描述方向以及会根据方向的描述确定物体的位置是解本题的关键.
11.(1)(2,4);(5,1);(5,4);(2)见解析.
【分析】(1)根据有序数对的定义分别写出即可;
(2)根据网格结构找出秋千的位置标注即可.
【详解】解:(1)(2,4);(5,1);(5,4);
(2)如图.
【点睛】本题考查坐标确定位置.
12.(1)见解析;
(2)点C在点B东北方向,距离点B的km处
【分析】(1)根据题意建立直角坐标系,再由坐标系写出点C的坐标即可;
(2)以点B为坐标中心,由方向角的定义可知点C在点B北偏东45°方向上,再由勾股定理求出BC的长.
【详解】(1)解:根据A(-3,1),B(-2,-3)画出直角坐标系,
描出点C(3,2),如图所示:
(2)由勾股定理可知,BC=5,
∴点C在点B北偏东45°方向上,距离点B的5km处.
【点睛】本题考查直角坐标系,用坐标系中的点表示位置、方向角、勾股定理等知识,是基础考点,掌握相关知识是解题关键.
13.(1),图见解析
(2)
(3)图见解析
【分析】(1)根据轴对称关系确定点、、的坐标,顺次连线即可;
(2)根据轴对称的性质解答即可;
(3)连接,与x轴交点即为点P.
【详解】(1)解:如下图所示.点的坐标为;
(2)解:直线m上各点的横坐标都为1,
,
由轴对称的性质可知,点关于直线m对称的点的横坐标为,纵坐标为b,
即点关于直线m对称的点的坐标为,
故答案为:;
(3)解:如图,连接,与x轴交点即为点P.
理由如下:
点C和点关于x轴对称,
,
,
即此时最小.
【点睛】本题考查轴对称的性质,利用轴对称关系作图,确定直角坐标系中点的坐标,最短路径问题作图,正确理解轴对称的性质是解题的关键.
14.(1)见解析
(2)的坐标为、的坐标为
(3)2
【分析】(1)根据轴对称的定义找到的三个顶点关于轴对称的点,再顺次连接即可;
(2)根据所作图形可得;
(3)利用割补法求解即可.
【详解】(1)解:如图所示,即为所求;
(2)由图象知的坐标为、的坐标为;
(3)的面积:.
【点睛】本题考查了轴对称变换,正确得出对应点位置是解题的关键.
15.(1),,,画图见解析;
(2)
(3)画图见解析,
【分析】(1)根据关于x轴对称的点的坐标特点可得、、的坐标,再顺次连接、、作三角形即可;
(2)由长方形的面积减去周围三个三角形的面积即可;
(3)如图,连接交x轴于点P,则的周长最小,再根据图形可得P的坐标.
【详解】(1)解:∵,,.
∴点A、B、C关于x轴的对称点、、的坐标为:
,,,
如图,即为所画的三角形,
(2).
(3)如图,连接交x轴于点P,
则,
∴,
此时的周长最小.
由作图可得:.
【点睛】本题考查的是画关于x轴对称的三角形,坐标与图形,求网格中三角形的面积,利用轴对称的性质确定三角形周长最小时点的位置与坐标,熟练的运用轴对称的性质进行解题是关键.
16.(1)
(2)或
(3)周长最小值为
【分析】(1)根据勾股定理直接进行计算即可求解;
(2)设,由点的坐标是,且,根据勾股定理建立方程,解方程即可求解.
(3)作点关于轴的对称点,根据对称性可得即为周长最小值,勾股定理求得即可求解.
【详解】(1)解:∵
∴,
故答案为:;
(2)设,∵点的坐标是,且,
∴,
解得,
∴点的坐标是:或,
故答案为:或;
(3)如图2,作点关于轴的对称点,则点,
∴,当三点共线时,最小,即周长最小,
∵,,,
,
,
∴△ABC周长最小值为:.
【点睛】本题考查了勾股定理求两点距离,轴对称的性质求线段和的最值问题,掌握勾股定理,轴对称的性质是解题的关键.
17.(1)图见解析,,,
(2)图见解析,点的坐标为
【分析】(1)分别作出点,,关于直线:的对称的点,然后顺次连接,并写出,,的坐标;
(2)作出点关于对称的点,连接,与的交点即为点,此时最小,写出点的坐标即可.
【详解】(1)解:如图,分别作出点,,关于直线:的对称的点,,,
连接,,,
则即为所作,
∴,,.
(2)如图,作点关于直线对称的点,连接,与直线的交点即为点,
∴直线为线段的垂直平分线,
∴,
∴,
∴此时最小,点坐标为.
故答案为:.
【点睛】本题考查根据轴对称变换作图,最短路线问题.解答本题的关键是根据网格结构作出对应点的位置并顺次连接.
18.(1)
(2)
【分析】(1)过点作于,则∠,,,,得出,由勾股定理求出即可;
(2)由题意得出最小,作关于y轴的对称点,连接交轴于点,点即为使最小的点,由勾股定理求出,即可求解;
【详解】(1)解:过点作于,如图,
则,
∵点的坐标分别为和,
∴,,,
∴,
∴;
(2)要使的周长最小,长度一定,
则最小,
作关于轴的对称点,连接交轴于点,过点作于点,如图,
∵,
∴当三点共线时,即与重合时,三角形的周长最小,最小值为的长,
由对称的性质得:,
∴
∴,
在中,,
∴,
∴的周长的最小值为.
【点睛】本题考查了勾股定理求两点距离,轴对称求线段和的最值问题,掌握轴对称的性质以及勾股定理是解题的关键.
19.(1)
(2)
(3)
【分析】(1)由非负数的性质求出,求出,由三点的坐标可求出答案;
(2)根据三角形的面积关系可得出答案;
(3)连接,设,由三角形面积关系得出,由平移的性质得出,根据三角形的面积关系可求出答案.
【详解】(1),,,
,,
,,
,
,,,
,,
;
(2)由题意知:,,
,
,
.
(3)连接,,
设,
,
,
,
点向右平移个单位长度得到点,
,
,
,
,
,
【点睛】本题是三角形综合题,考查了非负数的性质,坐标与图形的性质,平移的性质,三角形的面积等知识,解题的关键是学会利用参数构建方程解决问题.
20.(1)12;
(2)或;
(3)或.
【分析】(1)根据平移的性质求出点,的坐标,根据平行四边形的面积公式求出四边形的面积;
(2)根据三角形的面积公式计算即可;
(3)根据直线上点的坐标特征设出点的坐标,根据三角形的面积公式计算即可.
【详解】(1)解:(1)∵点,的坐标分别为,,线段先向上平移3个单位,再向右平移1个单位,得到线段,
∴点的坐标为,点的坐标为,,
∴四边形的面积;
(2)存在,
设点的坐标为,
由题意得:,
解得:,
∴点的坐标为或;
(3)设点的坐标为,
则,
由题意得:,
解得:或,
则点的坐标为或.
【点睛】本题考查的是平移的性质、三角形的面积计算、点的坐标特征,根据平移变换的性质求出点,的坐标是解题的关键.
21.(1)-3,4
(2)-3,4
(3)-4≤x≤-2且x≠-3
【分析】(1)根据非负数的性质构建方程组,解方程组求出,;
(2)过点作轴于,设,由三角形面积关系得出,求出,过点作轴于,由三角形面积关系得出,求出即可;
(3)连接,过点作轴,分点在第二象限,点在第三象限时,两种情况,分别列出方程,解之即可.
【详解】(1)解:,
又∵,,
,
解得:,
故答案为:-3,4.
(2)过点作轴于,
设,
三角形的面积四边形的面积三角形的面积,
,
即,
解得:,
点的坐标为,
过点作轴于,
三角形的面积三角形的面积三角形的面积,
,
即,
,
点的坐标为或.
(3)点向左平移4个单位长度,向下平移4个单位长度到点A,
∵点D向左平移4个单位长度后的对应点正好在y轴上,
∴点平移后的对应点恰好是点,
连接,过点作轴,如图所示:
,
三角形的面积三角形的面积,
当三角形的面积三角形的面积时,,
当点在第三象限时,
,
解得:,
当点在第二象限时,
,
解得:,
当三角形的面积不超过三角形面积的时,
点的横坐标的取值范围是,且.
【点睛】本题属于三角形综合题,考查了三角形的面积,非负数的性质,平行线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
答案第1页,共2页
答案第1页,共2页
