专题7.6平面直角坐标系中的图形变化及其应用 巩固篇 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题7.6平面直角坐标系中的图形变化及其应用 巩固篇 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 00:00:00 | ||
图片预览




文档简介
专题7.6 平面直角坐标系中的图形变化及其应用(巩固篇)(专项练习)
一、单选题
1.根据下列表述,能确定位置的是( )
A.北纬,东经 B.郑州市建设路
C.北偏东 D.郑东新区奥斯卡影院2排
2.已知点与关于x轴对称,则( )
A.1 B.0 C.4 D.2
3.在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
4.在平面直角坐标系xOy中,若在第三象限,则关于x轴对称的图形所在的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知两点A(﹣1,3),B(2,﹣3),现将线段AB平移至,如果(a,1),(5,﹣b),那么的值是( )
A.16 B.25 C.32 D.49
6.在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
7.三角形ABC在经过某次平移后,顶点A(﹣1,m+2)的对应点为A(2,m﹣3),若此三角形内任意一点P(a,b)经过此次平移后对应点P1(c,d).则a+b﹣c﹣d的值为( )
A.8+m B.﹣8+m C.2 D.﹣2
8.如图,已知点,,点P在直线上运动,则的最大值为( )
A. B. C.4 D.
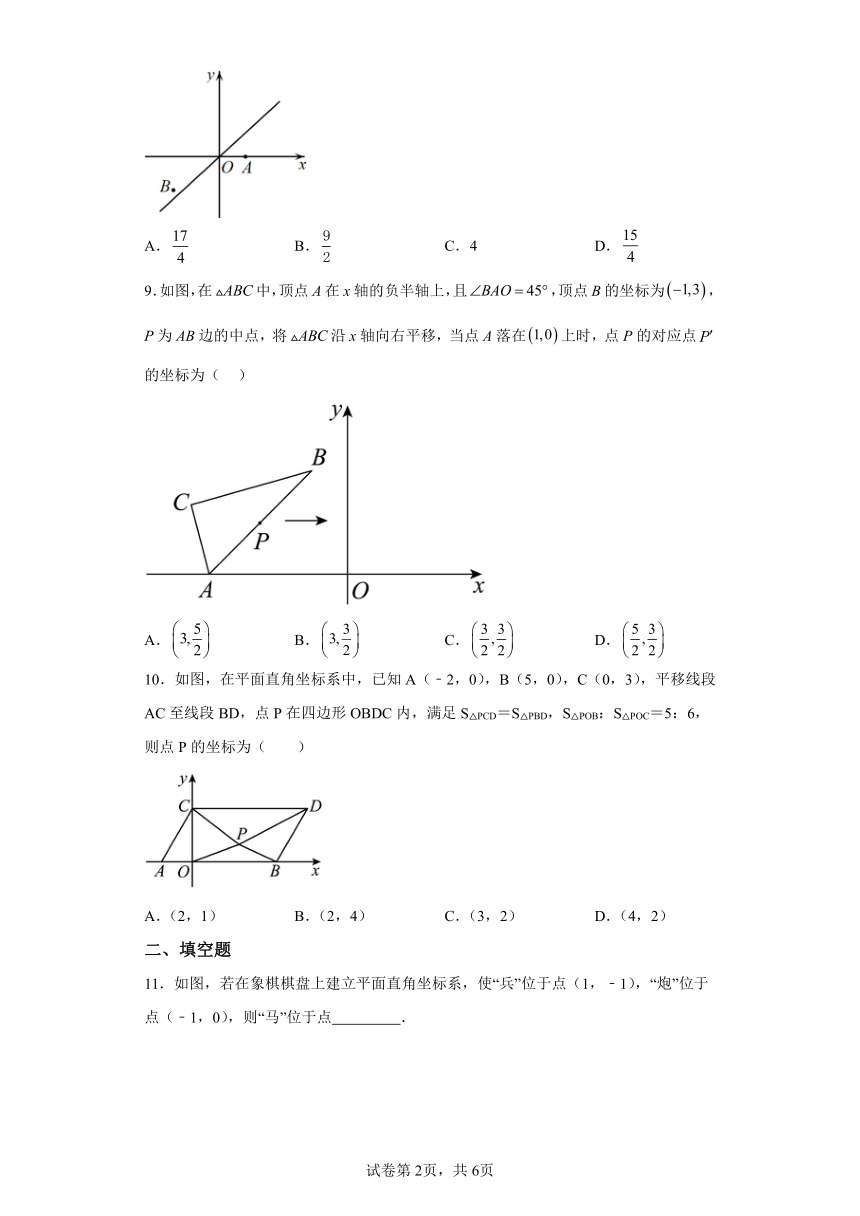
9.如图,在中,顶点A在x轴的负半轴上,且,顶点B的坐标为,P为AB边的中点,将沿x轴向右平移,当点A落在上时,点P的对应点的坐标为( )
A. B. C. D.
10.如图,在平面直角坐标系中,已知A(﹣2,0),B(5,0),C(0,3),平移线段AC至线段BD,点P在四边形OBDC内,满足S△PCD=S△PBD,S△POB:S△POC=5:6,则点P的坐标为( )
A.(2,1) B.(2,4) C.(3,2) D.(4,2)
二、填空题
11.如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,﹣1),“炮”位于点(﹣1,0),则“马”位于点 .
12.已知|m+5|+=0,点P(m,n)关于x轴的对称点的坐标是 .
13.若,则点先向左平移2个单位,再向下平移1个单位后的对应点,则点坐标为 .
14.点向左平移m个单位长度,再向上平移n个单位长度所得对应点,则的值为 .
15.如图,点向下平移n个单位后的点关于y轴的对称点为,则 .
16.如图,在平面直角坐标系中,,将点向下平移1个单位,再向右平移2个单位得到点,若点在轴上,且,则点的坐标为 .
17.如图,在平面直角坐标系中,点A的坐标是,点B的坐标是,在y轴和x轴上分别有两点P、Q,则A,B,P,Q四点组成的四边形的最小周长为 .
18.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,则D的坐标为 ,连接AC,BD.在y轴上存在一点P,连接PA,PB,使S四边形ABDC,则点P的坐标为 .
三、解答题
19.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)的面积为_______________;
(2)画出格点(顶点均在格点上)关于轴对称的;
(3)指出的顶点坐标:(,),(,),(,);
(4)在轴上画出点,使最小.
20.如图,在平面直角坐标系中.
(1)将向上平移2个单位长度,再向右平移两个单位长度得到,画出;
(2)写出点、、的坐标;
(3)直接写出的面积.
21.在平面直角坐标系中,O为原点,点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
(1)求b和k的值;(用含a的代数式表示k)
(2)探求当a变化时,三角形与三角形的面积大小关系.
22.如图所示,,点B在y轴上,将三角形沿x轴负方向平移,平移后的图形为三角形,点C的坐标为,且.
(1)直接写出点C的坐标 ;
(2)直接写出点E的坐标 ;
(3)点P是直线上一动点,设,,,确定x,y,z之间的数量关系,并证明你的结论.
23.如图,在平面直角坐标系中,点,过点作x轴的垂线l,点A关于直线l的对称点为B.
(1)点B的坐标为_____________;
(2)已知点,点,在图中描出点B,C,D,顺次连接点A,B,C,D.
①在四边形内部有一点P,满足且,则此时点P的坐标为_____________,_____________;
②在四边形外部是否存在点Q,满足且,若存在,直接写出点Q的坐标;若不存在,请说明理由.
24.如图,点A的坐标为,点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为.
(1)点E的坐标为________;点B的坐标为_______;
(2)在四边形ABCD中,点P从点B出发,沿“”移动.
①当点P在CD上时﹐设,试用含x,y的式子表示z,写出解答过程.
②当点P在BC上﹐且直线OP平分四边形ABCD的面积时﹐求点P的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据确定位置需要两个不同要素判定即可.
【详解】A.北纬,东经,能确定位置,故A符合题意;
B. 郑州市建设路,不能确定位置,故B不符合题意;
C.北偏东,不能确定位置,故C不符合题意;
D.郑东新区奥斯卡影院2排,不能确定位置,故D不符合题意.
故选:A.
【点睛】本题考查了位置的确定方法,熟练掌握位置确定的方法是解题的关键.
2.B
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数;可以直接写出答案.
【详解】解:∵点与关于轴对称,
∴,
∴,
故选:B.
【点睛】此题主要考查了关于x轴对称点的坐标特点,解决此类题目的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
3.D
【分析】根据点坐标特征、特殊直线的解析式可以作出判断 .
【详解】解:A、根据点坐标的符号特征,点A在第三象限,正确;
B、第二、四象限的角平分线为y=-x,并且点B坐标符合y=-x,正确;
C、线段AB为y=-3,平行于x轴,正确;
D、与点A关于y轴对称的点为(2,-3),错误;
故选D.
【点睛】本题考查点坐标的应用,熟练掌握点坐标特征及特殊直线的解析式是解题关键.
4.B
【分析】设内任一点A(a,b)在第三象限内,可得a<0,b<0,关于x轴对称后的点B(-a,b),则﹣a>0,b<0,然后判定象限即可.
【详解】解:∵设内任一点A(a,b)在第三象限内,
∴a<0,b<0,
∵点A关于x轴对称后的点B(a,-b),
∴﹣b>0,
∴点B(a,-b)所在的象限是第二象限,即在第二象限.
故选:B.
【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,熟练掌握四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)是解题的关键.
5.C
【分析】根据平移的性质,结合已知点A,B的坐标,根据平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减,可得出a,b的值,即可得到答案.
【详解】解:∵A(-1,3)平移后对应点的坐标为(a,1),
∴线段向下平移了2个单位,
∵点B(2,-3)平移后对应的点(5,-b),
∴线段向右平移了3个单位,
∴a=2,b=5,
∴,
故选:C.
【点睛】本题主要考查了点的平移规律与图形的平移,关键是掌握平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减,难度适中.
6.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
【详解】解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点睛】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
7.C
【分析】由A(-1,m+2)在经过此次平移后对应点A1(2,m-3),可得△ABC的平移规律为:向右平移3个单位,向下平移5个单位,由此得到结论.
【详解】解:∵A(-1,m+2)在经过此次平移后对应点A1(2,m-3),
∴△ABC的平移规律为:向右平移3个单位,向下平移5个单位,
∵点P(a,b)经过平移后对应点P1(c,d),
∴a+3=c,b-5=d,
∴a-c=-3,b-d=5,
∴a+b-c-d=-3+5=2,
故选:C.
【点睛】本题考查的是坐标与图形变化-平移,牢记平面直角坐标系内点的平移规律:上加下减、右加左减是解题的关键.
8.D
【分析】根据轴对称的性质可求得答案.
【详解】解:作A关于直线对称点C,
∴,
∵,
∴C的坐标为;
连接并延长,交直线于P点,
此时,取得最大值,
∴.
故选D.
【点睛】本题考查了一次函数图像上点的坐标特征,轴对称 最短路线问题,正确的作出辅助线是解决本题的关键.
9.D
【分析】先求出点A的坐标,然后利用中点坐标公式求出点P的坐标,将点P和点A向右平移相同的单位长度即可.
【详解】解:过点B作轴,垂足为D,如图,
∵B,,
为等腰直角三角形,
,
,
,
∵P为AB边的中点,
,即,
当点A落在上时,相当于将A水平向右平移了5个单位长度,
将向右平移5个单位长度后,即,
故选:D.
【点睛】本题考查了坐标与图形中的点的平移,等腰直角三角形的性质,中点坐标公式等,得到是由P向右平移5个单位长度得到的是解决这题的关键.
10.D
【分析】过P作PM⊥OB于M,并反向延长交CD于N,设P(x,y),根据S△POB:S△POC=5:6,于是得到x=2y;由于S△PCD=S△PBD,于是得到×7 (3-y)=18-×7(3-y)-×3x-×5y,最后解方程组即可得到结论.
【详解】解:如图,过P作PM⊥OB于M,交CD于N,
∵CD∥OB,
∴PN⊥CD,
设P(x,y),
∵S△POB:S△POC=5:6,
∴5××3x=6××5y,
∴x=2y,①
∵S△PCD=S△PBD,
∴×7 (3﹣y)=18﹣×7(3﹣y)﹣×3x﹣×5y,②
由①、②解得x=4,y=2,
∴P(4,2),
故选:D.
【点睛】本题主要考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,作辅助线构造平行线和垂线是解题的关键.
11.(4,﹣3)
【分析】由“兵”位于点(1,﹣1),“炮”位于点(﹣1,0),找出坐标原点,即可得出答案.
【详解】解:∵“兵”位于点(1,﹣1),“炮”位于点(﹣1,0),
∴坐标系如图:
∴“马”点的位于(4,﹣3).
故答案为:(4,﹣3).
【点睛】此题主要考查了坐标确定位置,正确建立平面直角坐标系是解题关键.
12.(﹣5,﹣3)
【分析】根据非负数的性质求得m、n的值,然后根据关于x轴对称的点的坐标特征即可解答.
【详解】解:∵|m+5|+=0,
∴m+5=0,n﹣3=0,
∴m=﹣5,n=3,
∴点P的坐标是(﹣5,3).
∴点P(m,n)关于x轴的对称点的坐标是 (﹣5,﹣3).
故填(﹣5,﹣3).
【点睛】本题主要考查了非负数的性质、平面直角坐标系中对称点的规律等知识点,根据非负数性质得出m、n的值是解答本题的关键.
13.
【分析】根据非负数的和为零,可得每个非负数同时为零,可得,的值,再根据坐标平移的变化规律即可求解.
【详解】解:,
,,
解得,,
,
点先向左平移2个单位,再向下平移1个单位后的对应点,
点的横坐标为,纵坐标为,
点的坐标为,
故答案为:.
【点睛】本题考查了坐标点的平移,偶次方的性质,算术平方根的性质,准确利用非负性求得点的坐标是解题的关键.
14.4
【分析】根据向左平移横坐标减,向上平移纵坐标加列方程求出m、n的值,再相加计算即可得解.
【详解】解:∵点向左平移m个单位长度,再向上平移n个单位长度所得对应点,
∴,,
解得m=1,n=3,
所以,m+n=1+3=4.
故答案为:4.
【点睛】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
15.3
【分析】根据关于y轴对称的规律和点平移的规律解答即可.
【详解】解:如下图,
∵点B(1, 1),点C、B关于y轴对称,
∴点C(-1, 1),
∵点A( 1,2),
∴点A( 1,2)向下平移3个单位后与点C重合,
∴n为3,
故答案为:3.
【点睛】本题考查了关于关于y轴对称的规律和点平移的规律,解题的关键是掌握关于x轴对称的点,横坐标相同,纵坐标互为相反数,关于 y 轴对称的点,纵坐标相同,横坐标互为相反数,关于原点对称的点,横坐标与纵坐标都互为相反数;在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移 a 个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数 a ,相应的新图形就是把原图形向上(或向下)平移 a 个单位长度(即:横坐标,右移加,左移减;纵坐标,上移加,下移减).
16.(0,2)或(0,)
【分析】根据题意确定点B的坐标,然后设C(0,m),结合图形,利用面积得出方程求解即可.
【详解】解:将点A向下平移1个单位,再向右平移2个单位得到点B,
∴B(0,),
设C(0,m),
如图所示,
根据题意得:,
解得:m=2或,
∴C(0,2)或(0,),
故答案为:(0,2)或(0,).
【点睛】题目主要考查坐标与图形,坐标的平移,一元一次方程的应用等,理解题意,综合运用这些知识点是解题关键.
17.##
【分析】作点A关于y轴的对称点C,点B关于x轴的对称点D,连接CD交y轴于P,交x轴于Q,则此时,四边形APQB的周长最小,且四边形的最小周长=AB+CD,根据两点间的距离公式即可得到结论.
【详解】解:作点A关于y轴的对称点C,点B关于x轴的对称点D,连接CD交y轴于p,交x轴于Q,则此时,四边形APQB的周长最小,且四边形的最小周长=AB+CD,
∵点A的坐标是(2,4),点B的坐标是(6,2),
∴C(-2,4),D(6,-2),
∵AB=,CD=,
∴四边形APQB的最小周长=10+,
故答案为:10+.
【点睛】本题考查了坐标与图形性质,轴对称-最短路径问题,两点间的距离公式,正确的确定点P和点Q的位置是解题的关键.
18. (4,2) (0,4)或(0,-4)
【分析】根据B点的平移方式即可得到D点的坐标;设点P到AB的距离为h,则S△PAB=×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标;
【详解】解:由题意得点D是点B(3,0)先向上平移2个单位,再向右平移1个单位的对应点,
∴点D的坐标为(4,2);
同理可得点C的坐标为(0,2),
∴OC=2,
∵A(-1,0),B(3,0),
∴AB=4,
∴,
设点P到AB的距离为h,
∴S△PAB=×AB×h=2h,
∵S△PAB=S四边形ABDC,
得2h=8,解得h=4,
∵P在y轴上,
∴OP=4,
∴P(0,4)或(0,-4).
故答案为:(4,2);(0,4)或(0,-4).
【点睛】本题主要考查了根据平移方式确定点的坐标,坐标与图形,解题时注意:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
19.(1)5
(2)详见解析
(3)
(4)详见解析
【分析】(1)用割补法求三角形的面积即可;
(2)先找出A、B、C、三点关于x轴的对称点,,,连接对称点即可;
(3)根据图象分析出三个点的坐标;
(4)根据轴对称的性质求解即可.
【详解】(1)解:,
故答案为:5.
(2)如图所示,即为所求;
(3)解:根据图象对称后的图象,可知每个顶点坐标为,
故答案为:.
(4)解:在图像上画出点关于y轴的对称点,连接,两点与轴的交点即为点,如下图所示:
【点睛】本题考查平面直角坐标系上的点,平面直角坐标系中关于x,y轴对称点的坐标特征,能够掌握数形结合思想是解决本题的关键.
20.(1)见解析
(2),,
(3)7
【分析】(1)根据平移的性质确定出点、、的位置,然后连线即可;
(2)根据图形写出坐标即可;
(3)用割补法求解即可.
【详解】(1)如图所示,即为所求.
(2)由图可知,,,.
(3)的面积.
【点睛】本题考查了平移作图,写出平面直角坐标系点的坐标,割补法求图形的面积,正确作出图形是解答本题的关键.
21.(1);;
(2)
【分析】(1)由,,结合,可得线段向上平移,再根据点的平移规则列方程即可;
(2)由平移的性质可得:,,如图,可得,过作于,过作于,显然,,从而可得答案.
【详解】(1)解:如图,∵点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
∴,,
∴,即,解得:,
∴,,,
∴,
解得:;
(2)由平移的性质可得:,,如图,
∴,
过作于,过作于,
显然,
∴,
∴,
∴.
【点睛】本题考查的是平移的性质,点的平移的坐标变化规律,平移的性质,平行线的性质,熟练地利用平移的性质解题是关键.
22.(1)
(2)
(3)①当点P在线段EC上时:;②当点P在线段的延长线上时:;③当点P在线段的延长线上时:
【分析】(1)直接利用算术平方根的性质得出a,b的值,即可得出答案;
(2)利用平移的性质得出点E的坐标;
(3)分三种情况讨论:①当点P在线段上时:如图,过点P作, ②当点P在线段的延长线上时,如图,过点P作, ③当点P在线段的延长线上时,再利用平行线的性质分析得出答案.
【详解】(1)解:∵
∴,,解得: ,,
∵点C的坐标为,
∴点C的坐标为:;
(2)∵点B在y轴上,点C的坐标为:,
∴B点向左平移了3个单位长度,
∴,向左平移3个单位得到:,
∴点E的坐标为:;
(3)①当点P在线段上时:
如图,过点P作,
∴,
又∵,
∴,
∴,
∴, 即.
②当点P在线段的延长线上时,
如图,过点P作,
∴,
又∵,
∴,
∴,
∴, 即.
③当点P在线段的延长线上时,
如图,过点P作,
∴,
又∵,
∴,
∴,
∴, 即.
【点睛】此题主要考查了平移的性质以及平行线的性质,算术平方根的非负性的应用,坐标与图形,清晰的分类讨论是解题关键.
23.(1).
(2)①,.②,理由见解析
【分析】(1)根据对称性可知点A和点B到直线l的距离相等,且纵坐标相等即可求解;
(2)①根据点A,B,C,D的坐标可得点A和点B关于直线l对称,点C和点D关于直线l对称,,,,由,可知点P在直线l上,设点P,再根据可得,求解即可得点P坐标,进而即可求解;
②与①同理,设,根据,可得,解方程进而即可求解.
【详解】(1)∵点坐标为,过点作x轴的垂线l,
∴点到直线l的距离为1,
∵点A和点B关于直线l的对称点,
∴,
故答案为:;
(2)如图所示:顺次连接A,B,C,D,可以发现四边形是等腰梯形,且关于直线对称,
①∵点,点,点,点,
∴点A和点B关于直线l对称,点C和点D关于直线l对称,,,,
∵在四边形内部有一点P,满足,
则点P在直线l上,设点P,
∵,
∴,即,
整理得:,
解得:,
∴点,
∴,
故答案为:,;
②存在,
理由:∵
∴点Q在对称轴上,
设,
∵,
∴,即,
解得:,
∴点.
【点睛】本题考查坐标与图形—对称,三角形面积等知识,解题的关键是学会利用数形结合的思想和参数构造方程解决问题.
24.(1)(-2,0);(0,2).
(2)① ②
【分析】(1)依据平移的性质可知轴,BC=AE=3,然后依据点A和点C的坐标可得到点B和点E的坐标;
(2)①过点P作交AB于点F,则,然后依据平行线的性质可得到∠BPF=∠CBP=x,∠APF=∠DAP=y,最后,再依据角的和差关系进行解答即可;②先求解四边形ABCD的面积,再画出图形,结合直线OP平分四边形ABCD的面积建立方程求解即可.
【详解】(1)解: ∵将三角形OAB沿x轴负方向平移,C(-3,2),A(1,0),
∴轴,BC=AE=3.
∴B(0,2),E(-2,0).
故答案为:(-2,0);(0,2).
(2)①∵点P在线段CD上时,
如图,过点P作交AB于点F,则,
∴∠BPF=∠CBP=x,∠APF=∠DAP=y,
∴∠BPA=∠BPF+∠APF=x+y=z,
∴z=x+y.
②∵由平移的性质可得:轴, 而
∴
∵
∴ 而
∴
如图,当点P在BC上﹐且直线OP平分四边形ABCD的面积时﹐
∴
∴
∴
∴
【点睛】本题考查的是平移的性质,坐标与图形,平行线的判定与性质,图形面积的计算,掌握“坐标与图形中线段的长度的对应关系以及平移的性质”是解本题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.根据下列表述,能确定位置的是( )
A.北纬,东经 B.郑州市建设路
C.北偏东 D.郑东新区奥斯卡影院2排
2.已知点与关于x轴对称,则( )
A.1 B.0 C.4 D.2
3.在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
4.在平面直角坐标系xOy中,若在第三象限,则关于x轴对称的图形所在的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知两点A(﹣1,3),B(2,﹣3),现将线段AB平移至,如果(a,1),(5,﹣b),那么的值是( )
A.16 B.25 C.32 D.49
6.在平面直角坐标系中,将点向右平移2个单位长度,再向下平移2个单位长度所得到的点坐标为( )
A. B. C. D.
7.三角形ABC在经过某次平移后,顶点A(﹣1,m+2)的对应点为A(2,m﹣3),若此三角形内任意一点P(a,b)经过此次平移后对应点P1(c,d).则a+b﹣c﹣d的值为( )
A.8+m B.﹣8+m C.2 D.﹣2
8.如图,已知点,,点P在直线上运动,则的最大值为( )
A. B. C.4 D.
9.如图,在中,顶点A在x轴的负半轴上,且,顶点B的坐标为,P为AB边的中点,将沿x轴向右平移,当点A落在上时,点P的对应点的坐标为( )
A. B. C. D.
10.如图,在平面直角坐标系中,已知A(﹣2,0),B(5,0),C(0,3),平移线段AC至线段BD,点P在四边形OBDC内,满足S△PCD=S△PBD,S△POB:S△POC=5:6,则点P的坐标为( )
A.(2,1) B.(2,4) C.(3,2) D.(4,2)
二、填空题
11.如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,﹣1),“炮”位于点(﹣1,0),则“马”位于点 .
12.已知|m+5|+=0,点P(m,n)关于x轴的对称点的坐标是 .
13.若,则点先向左平移2个单位,再向下平移1个单位后的对应点,则点坐标为 .
14.点向左平移m个单位长度,再向上平移n个单位长度所得对应点,则的值为 .
15.如图,点向下平移n个单位后的点关于y轴的对称点为,则 .
16.如图,在平面直角坐标系中,,将点向下平移1个单位,再向右平移2个单位得到点,若点在轴上,且,则点的坐标为 .
17.如图,在平面直角坐标系中,点A的坐标是,点B的坐标是,在y轴和x轴上分别有两点P、Q,则A,B,P,Q四点组成的四边形的最小周长为 .
18.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,则D的坐标为 ,连接AC,BD.在y轴上存在一点P,连接PA,PB,使S四边形ABDC,则点P的坐标为 .
三、解答题
19.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)的面积为_______________;
(2)画出格点(顶点均在格点上)关于轴对称的;
(3)指出的顶点坐标:(,),(,),(,);
(4)在轴上画出点,使最小.
20.如图,在平面直角坐标系中.
(1)将向上平移2个单位长度,再向右平移两个单位长度得到,画出;
(2)写出点、、的坐标;
(3)直接写出的面积.
21.在平面直角坐标系中,O为原点,点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
(1)求b和k的值;(用含a的代数式表示k)
(2)探求当a变化时,三角形与三角形的面积大小关系.
22.如图所示,,点B在y轴上,将三角形沿x轴负方向平移,平移后的图形为三角形,点C的坐标为,且.
(1)直接写出点C的坐标 ;
(2)直接写出点E的坐标 ;
(3)点P是直线上一动点,设,,,确定x,y,z之间的数量关系,并证明你的结论.
23.如图,在平面直角坐标系中,点,过点作x轴的垂线l,点A关于直线l的对称点为B.
(1)点B的坐标为_____________;
(2)已知点,点,在图中描出点B,C,D,顺次连接点A,B,C,D.
①在四边形内部有一点P,满足且,则此时点P的坐标为_____________,_____________;
②在四边形外部是否存在点Q,满足且,若存在,直接写出点Q的坐标;若不存在,请说明理由.
24.如图,点A的坐标为,点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为.
(1)点E的坐标为________;点B的坐标为_______;
(2)在四边形ABCD中,点P从点B出发,沿“”移动.
①当点P在CD上时﹐设,试用含x,y的式子表示z,写出解答过程.
②当点P在BC上﹐且直线OP平分四边形ABCD的面积时﹐求点P的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据确定位置需要两个不同要素判定即可.
【详解】A.北纬,东经,能确定位置,故A符合题意;
B. 郑州市建设路,不能确定位置,故B不符合题意;
C.北偏东,不能确定位置,故C不符合题意;
D.郑东新区奥斯卡影院2排,不能确定位置,故D不符合题意.
故选:A.
【点睛】本题考查了位置的确定方法,熟练掌握位置确定的方法是解题的关键.
2.B
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数;可以直接写出答案.
【详解】解:∵点与关于轴对称,
∴,
∴,
故选:B.
【点睛】此题主要考查了关于x轴对称点的坐标特点,解决此类题目的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
3.D
【分析】根据点坐标特征、特殊直线的解析式可以作出判断 .
【详解】解:A、根据点坐标的符号特征,点A在第三象限,正确;
B、第二、四象限的角平分线为y=-x,并且点B坐标符合y=-x,正确;
C、线段AB为y=-3,平行于x轴,正确;
D、与点A关于y轴对称的点为(2,-3),错误;
故选D.
【点睛】本题考查点坐标的应用,熟练掌握点坐标特征及特殊直线的解析式是解题关键.
4.B
【分析】设内任一点A(a,b)在第三象限内,可得a<0,b<0,关于x轴对称后的点B(-a,b),则﹣a>0,b<0,然后判定象限即可.
【详解】解:∵设内任一点A(a,b)在第三象限内,
∴a<0,b<0,
∵点A关于x轴对称后的点B(a,-b),
∴﹣b>0,
∴点B(a,-b)所在的象限是第二象限,即在第二象限.
故选:B.
【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,熟练掌握四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)是解题的关键.
5.C
【分析】根据平移的性质,结合已知点A,B的坐标,根据平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减,可得出a,b的值,即可得到答案.
【详解】解:∵A(-1,3)平移后对应点的坐标为(a,1),
∴线段向下平移了2个单位,
∵点B(2,-3)平移后对应的点(5,-b),
∴线段向右平移了3个单位,
∴a=2,b=5,
∴,
故选:C.
【点睛】本题主要考查了点的平移规律与图形的平移,关键是掌握平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减,难度适中.
6.D
【分析】根据“横坐标右移加,左移减;纵坐标上移加,下移减”的规律求解即可.
【详解】解:将点P(3,2)向右平移2个单位长度得到(5,2),
再向下平移2个单位长度,所得到的点坐标为(5,0).
故选:D.
【点睛】本题考查了坐标与图形变化——平移:向右平移a个单位,坐标P(x,y) (x+a,y);向左平移a个单位,坐标P(x,y)(x-a,y);向上平移b个单位,坐标P(x,y)(x,y+b);向下平移b个单位,坐标P(x,y)(x,y-b),熟记点的坐标的平移规则是解题的关键.
7.C
【分析】由A(-1,m+2)在经过此次平移后对应点A1(2,m-3),可得△ABC的平移规律为:向右平移3个单位,向下平移5个单位,由此得到结论.
【详解】解:∵A(-1,m+2)在经过此次平移后对应点A1(2,m-3),
∴△ABC的平移规律为:向右平移3个单位,向下平移5个单位,
∵点P(a,b)经过平移后对应点P1(c,d),
∴a+3=c,b-5=d,
∴a-c=-3,b-d=5,
∴a+b-c-d=-3+5=2,
故选:C.
【点睛】本题考查的是坐标与图形变化-平移,牢记平面直角坐标系内点的平移规律:上加下减、右加左减是解题的关键.
8.D
【分析】根据轴对称的性质可求得答案.
【详解】解:作A关于直线对称点C,
∴,
∵,
∴C的坐标为;
连接并延长,交直线于P点,
此时,取得最大值,
∴.
故选D.
【点睛】本题考查了一次函数图像上点的坐标特征,轴对称 最短路线问题,正确的作出辅助线是解决本题的关键.
9.D
【分析】先求出点A的坐标,然后利用中点坐标公式求出点P的坐标,将点P和点A向右平移相同的单位长度即可.
【详解】解:过点B作轴,垂足为D,如图,
∵B,,
为等腰直角三角形,
,
,
,
∵P为AB边的中点,
,即,
当点A落在上时,相当于将A水平向右平移了5个单位长度,
将向右平移5个单位长度后,即,
故选:D.
【点睛】本题考查了坐标与图形中的点的平移,等腰直角三角形的性质,中点坐标公式等,得到是由P向右平移5个单位长度得到的是解决这题的关键.
10.D
【分析】过P作PM⊥OB于M,并反向延长交CD于N,设P(x,y),根据S△POB:S△POC=5:6,于是得到x=2y;由于S△PCD=S△PBD,于是得到×7 (3-y)=18-×7(3-y)-×3x-×5y,最后解方程组即可得到结论.
【详解】解:如图,过P作PM⊥OB于M,交CD于N,
∵CD∥OB,
∴PN⊥CD,
设P(x,y),
∵S△POB:S△POC=5:6,
∴5××3x=6××5y,
∴x=2y,①
∵S△PCD=S△PBD,
∴×7 (3﹣y)=18﹣×7(3﹣y)﹣×3x﹣×5y,②
由①、②解得x=4,y=2,
∴P(4,2),
故选:D.
【点睛】本题主要考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,作辅助线构造平行线和垂线是解题的关键.
11.(4,﹣3)
【分析】由“兵”位于点(1,﹣1),“炮”位于点(﹣1,0),找出坐标原点,即可得出答案.
【详解】解:∵“兵”位于点(1,﹣1),“炮”位于点(﹣1,0),
∴坐标系如图:
∴“马”点的位于(4,﹣3).
故答案为:(4,﹣3).
【点睛】此题主要考查了坐标确定位置,正确建立平面直角坐标系是解题关键.
12.(﹣5,﹣3)
【分析】根据非负数的性质求得m、n的值,然后根据关于x轴对称的点的坐标特征即可解答.
【详解】解:∵|m+5|+=0,
∴m+5=0,n﹣3=0,
∴m=﹣5,n=3,
∴点P的坐标是(﹣5,3).
∴点P(m,n)关于x轴的对称点的坐标是 (﹣5,﹣3).
故填(﹣5,﹣3).
【点睛】本题主要考查了非负数的性质、平面直角坐标系中对称点的规律等知识点,根据非负数性质得出m、n的值是解答本题的关键.
13.
【分析】根据非负数的和为零,可得每个非负数同时为零,可得,的值,再根据坐标平移的变化规律即可求解.
【详解】解:,
,,
解得,,
,
点先向左平移2个单位,再向下平移1个单位后的对应点,
点的横坐标为,纵坐标为,
点的坐标为,
故答案为:.
【点睛】本题考查了坐标点的平移,偶次方的性质,算术平方根的性质,准确利用非负性求得点的坐标是解题的关键.
14.4
【分析】根据向左平移横坐标减,向上平移纵坐标加列方程求出m、n的值,再相加计算即可得解.
【详解】解:∵点向左平移m个单位长度,再向上平移n个单位长度所得对应点,
∴,,
解得m=1,n=3,
所以,m+n=1+3=4.
故答案为:4.
【点睛】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
15.3
【分析】根据关于y轴对称的规律和点平移的规律解答即可.
【详解】解:如下图,
∵点B(1, 1),点C、B关于y轴对称,
∴点C(-1, 1),
∵点A( 1,2),
∴点A( 1,2)向下平移3个单位后与点C重合,
∴n为3,
故答案为:3.
【点睛】本题考查了关于关于y轴对称的规律和点平移的规律,解题的关键是掌握关于x轴对称的点,横坐标相同,纵坐标互为相反数,关于 y 轴对称的点,纵坐标相同,横坐标互为相反数,关于原点对称的点,横坐标与纵坐标都互为相反数;在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移 a 个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数 a ,相应的新图形就是把原图形向上(或向下)平移 a 个单位长度(即:横坐标,右移加,左移减;纵坐标,上移加,下移减).
16.(0,2)或(0,)
【分析】根据题意确定点B的坐标,然后设C(0,m),结合图形,利用面积得出方程求解即可.
【详解】解:将点A向下平移1个单位,再向右平移2个单位得到点B,
∴B(0,),
设C(0,m),
如图所示,
根据题意得:,
解得:m=2或,
∴C(0,2)或(0,),
故答案为:(0,2)或(0,).
【点睛】题目主要考查坐标与图形,坐标的平移,一元一次方程的应用等,理解题意,综合运用这些知识点是解题关键.
17.##
【分析】作点A关于y轴的对称点C,点B关于x轴的对称点D,连接CD交y轴于P,交x轴于Q,则此时,四边形APQB的周长最小,且四边形的最小周长=AB+CD,根据两点间的距离公式即可得到结论.
【详解】解:作点A关于y轴的对称点C,点B关于x轴的对称点D,连接CD交y轴于p,交x轴于Q,则此时,四边形APQB的周长最小,且四边形的最小周长=AB+CD,
∵点A的坐标是(2,4),点B的坐标是(6,2),
∴C(-2,4),D(6,-2),
∵AB=,CD=,
∴四边形APQB的最小周长=10+,
故答案为:10+.
【点睛】本题考查了坐标与图形性质,轴对称-最短路径问题,两点间的距离公式,正确的确定点P和点Q的位置是解题的关键.
18. (4,2) (0,4)或(0,-4)
【分析】根据B点的平移方式即可得到D点的坐标;设点P到AB的距离为h,则S△PAB=×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标;
【详解】解:由题意得点D是点B(3,0)先向上平移2个单位,再向右平移1个单位的对应点,
∴点D的坐标为(4,2);
同理可得点C的坐标为(0,2),
∴OC=2,
∵A(-1,0),B(3,0),
∴AB=4,
∴,
设点P到AB的距离为h,
∴S△PAB=×AB×h=2h,
∵S△PAB=S四边形ABDC,
得2h=8,解得h=4,
∵P在y轴上,
∴OP=4,
∴P(0,4)或(0,-4).
故答案为:(4,2);(0,4)或(0,-4).
【点睛】本题主要考查了根据平移方式确定点的坐标,坐标与图形,解题时注意:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
19.(1)5
(2)详见解析
(3)
(4)详见解析
【分析】(1)用割补法求三角形的面积即可;
(2)先找出A、B、C、三点关于x轴的对称点,,,连接对称点即可;
(3)根据图象分析出三个点的坐标;
(4)根据轴对称的性质求解即可.
【详解】(1)解:,
故答案为:5.
(2)如图所示,即为所求;
(3)解:根据图象对称后的图象,可知每个顶点坐标为,
故答案为:.
(4)解:在图像上画出点关于y轴的对称点,连接,两点与轴的交点即为点,如下图所示:
【点睛】本题考查平面直角坐标系上的点,平面直角坐标系中关于x,y轴对称点的坐标特征,能够掌握数形结合思想是解决本题的关键.
20.(1)见解析
(2),,
(3)7
【分析】(1)根据平移的性质确定出点、、的位置,然后连线即可;
(2)根据图形写出坐标即可;
(3)用割补法求解即可.
【详解】(1)如图所示,即为所求.
(2)由图可知,,,.
(3)的面积.
【点睛】本题考查了平移作图,写出平面直角坐标系点的坐标,割补法求图形的面积,正确作出图形是解答本题的关键.
21.(1);;
(2)
【分析】(1)由,,结合,可得线段向上平移,再根据点的平移规则列方程即可;
(2)由平移的性质可得:,,如图,可得,过作于,过作于,显然,,从而可得答案.
【详解】(1)解:如图,∵点,点,且点B在A的右边.将线段平移,平移后A,B的对应点分别为点,,其中,.
∴,,
∴,即,解得:,
∴,,,
∴,
解得:;
(2)由平移的性质可得:,,如图,
∴,
过作于,过作于,
显然,
∴,
∴,
∴.
【点睛】本题考查的是平移的性质,点的平移的坐标变化规律,平移的性质,平行线的性质,熟练地利用平移的性质解题是关键.
22.(1)
(2)
(3)①当点P在线段EC上时:;②当点P在线段的延长线上时:;③当点P在线段的延长线上时:
【分析】(1)直接利用算术平方根的性质得出a,b的值,即可得出答案;
(2)利用平移的性质得出点E的坐标;
(3)分三种情况讨论:①当点P在线段上时:如图,过点P作, ②当点P在线段的延长线上时,如图,过点P作, ③当点P在线段的延长线上时,再利用平行线的性质分析得出答案.
【详解】(1)解:∵
∴,,解得: ,,
∵点C的坐标为,
∴点C的坐标为:;
(2)∵点B在y轴上,点C的坐标为:,
∴B点向左平移了3个单位长度,
∴,向左平移3个单位得到:,
∴点E的坐标为:;
(3)①当点P在线段上时:
如图,过点P作,
∴,
又∵,
∴,
∴,
∴, 即.
②当点P在线段的延长线上时,
如图,过点P作,
∴,
又∵,
∴,
∴,
∴, 即.
③当点P在线段的延长线上时,
如图,过点P作,
∴,
又∵,
∴,
∴,
∴, 即.
【点睛】此题主要考查了平移的性质以及平行线的性质,算术平方根的非负性的应用,坐标与图形,清晰的分类讨论是解题关键.
23.(1).
(2)①,.②,理由见解析
【分析】(1)根据对称性可知点A和点B到直线l的距离相等,且纵坐标相等即可求解;
(2)①根据点A,B,C,D的坐标可得点A和点B关于直线l对称,点C和点D关于直线l对称,,,,由,可知点P在直线l上,设点P,再根据可得,求解即可得点P坐标,进而即可求解;
②与①同理,设,根据,可得,解方程进而即可求解.
【详解】(1)∵点坐标为,过点作x轴的垂线l,
∴点到直线l的距离为1,
∵点A和点B关于直线l的对称点,
∴,
故答案为:;
(2)如图所示:顺次连接A,B,C,D,可以发现四边形是等腰梯形,且关于直线对称,
①∵点,点,点,点,
∴点A和点B关于直线l对称,点C和点D关于直线l对称,,,,
∵在四边形内部有一点P,满足,
则点P在直线l上,设点P,
∵,
∴,即,
整理得:,
解得:,
∴点,
∴,
故答案为:,;
②存在,
理由:∵
∴点Q在对称轴上,
设,
∵,
∴,即,
解得:,
∴点.
【点睛】本题考查坐标与图形—对称,三角形面积等知识,解题的关键是学会利用数形结合的思想和参数构造方程解决问题.
24.(1)(-2,0);(0,2).
(2)① ②
【分析】(1)依据平移的性质可知轴,BC=AE=3,然后依据点A和点C的坐标可得到点B和点E的坐标;
(2)①过点P作交AB于点F,则,然后依据平行线的性质可得到∠BPF=∠CBP=x,∠APF=∠DAP=y,最后,再依据角的和差关系进行解答即可;②先求解四边形ABCD的面积,再画出图形,结合直线OP平分四边形ABCD的面积建立方程求解即可.
【详解】(1)解: ∵将三角形OAB沿x轴负方向平移,C(-3,2),A(1,0),
∴轴,BC=AE=3.
∴B(0,2),E(-2,0).
故答案为:(-2,0);(0,2).
(2)①∵点P在线段CD上时,
如图,过点P作交AB于点F,则,
∴∠BPF=∠CBP=x,∠APF=∠DAP=y,
∴∠BPA=∠BPF+∠APF=x+y=z,
∴z=x+y.
②∵由平移的性质可得:轴, 而
∴
∵
∴ 而
∴
如图,当点P在BC上﹐且直线OP平分四边形ABCD的面积时﹐
∴
∴
∴
∴
【点睛】本题考查的是平移的性质,坐标与图形,平行线的判定与性质,图形面积的计算,掌握“坐标与图形中线段的长度的对应关系以及平移的性质”是解本题的关键.
答案第1页,共2页
答案第1页,共2页
