第10章 轴对称平移与旋转教案
图片预览




文档简介
第10章 轴 对 称、平移与旋转
10、1生活中的轴对称
第一课时 生活中的轴对称
教学目的
1.通过展示轴对称图形的图片,使学生初步认识轴对称图形;
2.通过试验,归纳出轴对称图形概念,能用概念判断一个图形是否是轴对称图形;
3.培养学生的动手试验能力、归纳能力和语言表述能力。
重点、难点
轴对称图形的概念是教学重点,判断图形是否是轴对称图形既是教学重点又是教学难点。
教具准备
一些关于轴对称的图片、半透明纸张。
教学过程
一、引入
1.展示图片,认识一些轴对称图形。
自远古以来,对称形式被认为是和谐美丽、并且真实的,不论是在自然界中还是建筑里,甚至最普通的日常生活用品中,对称的形式随处可见,青山倒映在水中,这是令人难忘的对称景象。同学们可以想象,当你放学回家,落日、晚霞、还有远处的青山倒映在平静的水中,这样如诗如画的景致怎能不令人难忘,
2.课上展开讨论,列举出一些现实生活中有关轴对称的物体和建筑物。
二、新课
1.试验
把一张半透明纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形?
由教师先示范剪出一个图形,而后由同学们自由发挥想象,剪出图案。
2.由展示的图片和同学们剪出的图案归纳轴对称图形的概念。
从同学们剪出的图案和展示的图片来看,这些图形如果沿着某条直线对折,对折的两部分是完全重合的,这样的图形称为轴对称图形这条直线叫做这个图形的对称轴。
三、练习
1.要求同学们找出所剪的图案的对称轴,并且用直尺把它画出来。
2.结合展示图片,让同学们找对称轴,并使同学们知道有的轴对称图形不止一条对称轴。3.给每位同学发一张半透明的画有如右图所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有几条对称轴。
四、课堂小结
本节课认识了什么样的图形是轴对称图形,这些图形都有共同的特点,就是沿着某条直线对折,直线两旁的图形完全重合,这条直线称为这个图形的对称轴。值得同学们注意的是,有的轴对称图形的对称轴不止一条,例如,练习第3题中的星形图就有六条对称轴。
五、作业
1.第82页练习第1、2题。
2.第82页习题10.1练习第1、2题
课后反思:
第二课时 生活中的轴对称
教学目的
使学生进一步认识轴对称图形,通过动手实验,掌握关于某条直线成轴对称的两个图形的对应线段相等、对应角相等;理解轴对称图形和两个图形成轴对称这两个概念的区别与联系。
重点、难点
重点:轴对称图形的对应线段相等、对应角相等。
难点:两个图形成轴对称与轴对称图形两个概念的区别与联系。
一、复习、评讲
1.复习轴对称图形的定义。
2.评讲上节课的作业,使学生进一步掌握判断一个图形是否是轴对称图形。
二、新课
1.什么是两个图形成轴对称?
试验:发给每位同学右边两个图形的纸张,把纸张沿着虚线折叠,观察对折后的左边部分和右边部分是否完全重合?
像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两图形重合时互相重合的点)叫做对称点。
练习:在上图的(2)中,把A、B、C的对称点标出来。
试验:在纸上滴上墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称?它的对称轴是哪一条?把它画出来。
2.轴对称图形(或关于某条直线成对称的两个图形)沿对称轴对折后的两部分完全重合,所以它的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等。
3.轴对称图形与两个图形成轴对称的区别与联系.
如图(1),如果沿着虚线对折,直线两旁的部分会完全重合,那么这个图形就是轴对称图形;若把这个图形看成是左右两部分,则这两个图形就是关于虚线这条直线成轴对称。
如图(2),如果沿着虚线折叠,右边的图形会与左边的图形完全重合,那么就说这两个图形关于虚线这条直线成轴对称,若把(2)中的左右两个四边形看成是一个整体的图形,那么这个整体的图形是轴对称图形。
因此,轴对称图形和两个图形成轴对称的本质是相同的,只是怎么看图形的问题。
三、巩固练习
1.下面哪些选项的右边图形与左边图形成轴对称?
2.如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等?哪些线段相等?
四、课堂小结成轴对称的两个图形是完全重合的,因此,它们的对应线段相等,对应角相等;知道轴对称和轴对称图形的区别与联系。
五、作业
课本P82习题第3、4题。
课后反思:
10.2 轴对称的认识
1.简单的轴对称图形
第一课时 线段的垂直平分线
教学目的
通过动手试验,使学生知道线段是轴对称图形,掌握线段的垂直子分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。
重点、难点
重点:线段垂直平分线上的点到线段两端的距离相等。
难点:运用线段垂直平分线性质解决问题。
教学过程
一、复习引入
1.轴对称图形的定义是什么?
2.线段是轴对称图形吗?它的两个端点是否关于某条直线成轴对称?
二、新课
1.认识线段是轴对称图形,引出线段垂直平分线的定义。
试验:按以下方法,看看线段是否是轴对称图形?
在半透明纸上画出线段AB和它和中点O,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合?
显然,线段OA和OB互相重合,因此,线段是轴对称图形。那么,线段的对称轴是哪一条呢?
线段垂直平分线的定义:垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线。如上图的直线 CD就是线段AB的垂直平分线。
2.线段垂直平分线上的点到线段两端的距离相等。
在以上试验的基础上,同学们在直线CD上任意取一点M,连结 MA、MB,而后沿着直线CD折叠,观察MA和MB是否重合?再取一点试试,观察PA和PB是否重合?待同学们实验完毕,引导同学们归纳线段垂直平分线的性质。
线段垂直平分线上的点到线段两端的距离相等。
3.线段垂直平分线性质的应用举例。
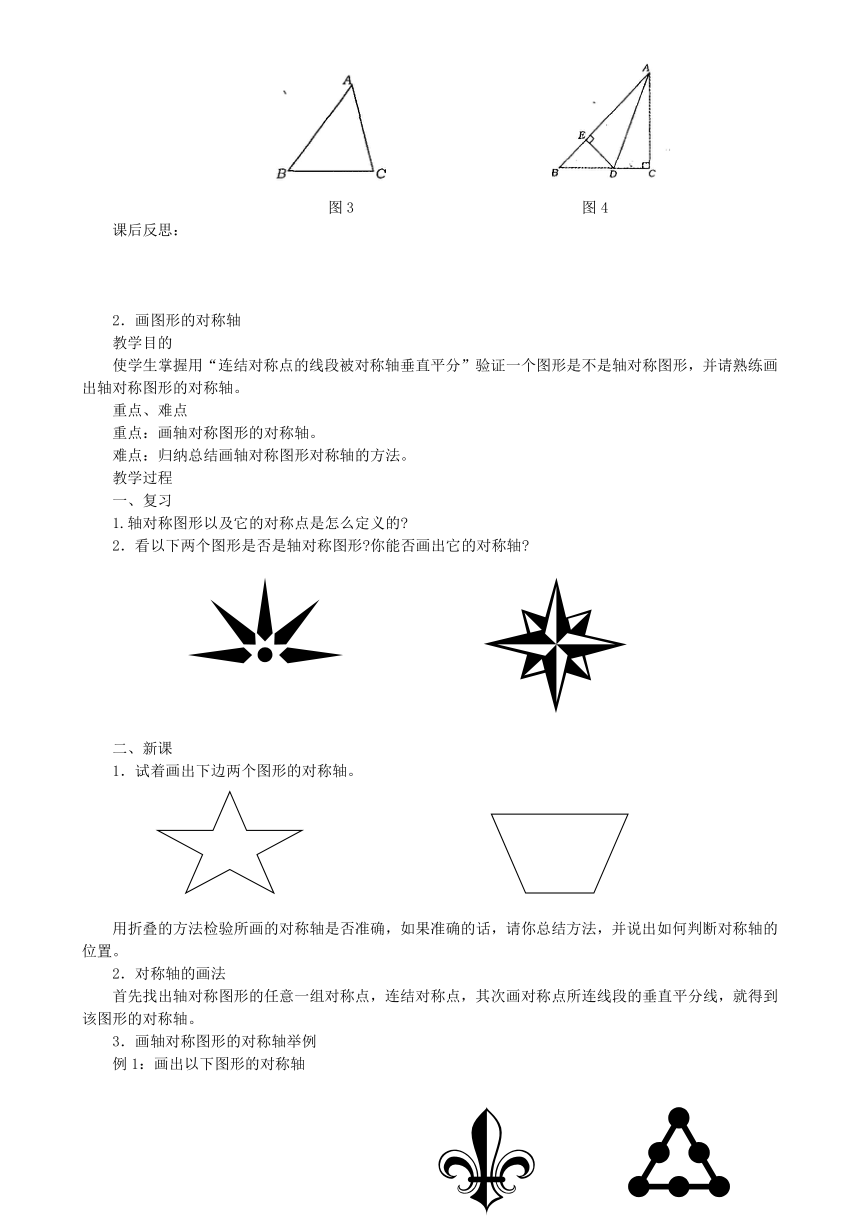
例1.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
分析:要求△BCE的周长,需知道BE、CE、BC的长度,从题目给出的条件来看,BE、BC的长度已经知道,而正点是线段BC的垂直平分线上的点,所以CE=BE,从而问题得到解决。
例2.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗?为什么?
三、课堂练习
课本P85练习第1、2题
四、课堂小结
线段垂直平分线的性质及其运用是本节课的重点,应用其性质我们可以证明两条线段相等。
作业
1、如图1,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
图1 图2
2.如图2,△BAC=120°,∠C=30°,DE是线段AC的垂直平分线,求:∠BAD的度数。
课后反思:
第二课时 角平分线
教学目的
使学生知道角是轴对称图形,对称轴是角平分线所在的直线,掌握角平分线的性质,并能运用它解决相关问题。
重点、难点
重点:角平分线上的点到角两边的距离相等。
难点:运用角平分线性质解决问题。
教学过程
一、复习引入
1.点到直线的距离的定义是什么?
2.角是轴对称图形吗?对称轴是哪一条直线?
二、新课
1.认识角是轴对称图形,知道角平分线所在的直线是它的对称轴。
试验:按以下方法试验,使同学认识角是轴对称图形。
在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM。
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线。
2.角平分线上的点到角两边的距离相等。
在以上试验的基础上,同学们在射线OM上任取一点P,过P点分别作OA和OB的垂线PC和PD,而后沿着OM折叠,观察PC和 PD是否重合?再取一点,按上述同样的方法试验,待同学们试验完毕,引导同学归纳角平分线的性质。
角平分线上的点到角两边的距离相等。
3.角平分线性质应用举例
例1.如下图(1)所示,在△ABC中,∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD和3DC是什么关系?为什么?
图(1) 图(2)
例2.如上图(2),BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,P=3cm,求 P点到直线AB的距离。
三、课堂练习
(课本P86第3、4题)
四、课堂小结
角是轴对称图形,对称轴是角平分线所在的直线。运用角平分线性质可以说明两条线段相等。
五、作业
1.如图3,AD平分∠BAC,∠C=90°,DE⊥ AB,那么(1)DE和DC相等吗?为什么? (2)AE和AC相等吗?为什么?
2.如图4,在△ABC中,用直尺、量角器画∠A、∠B、∠C的平分线,看看三条角平分线有什么关系?
图3 图4
课后反思:
2.画图形的对称轴
教学目的
使学生掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并请熟练画出轴对称图形的对称轴。
重点、难点
重点:画轴对称图形的对称轴。
难点:归纳总结画轴对称图形对称轴的方法。
教学过程
一、复习
1.轴对称图形以及它的对称点是怎么定义的?
2.看以下两个图形是否是轴对称图形?你能否画出它的对称轴?
二、新课
1.试着画出下边两个图形的对称轴。
用折叠的方法检验所画的对称轴是否准确,如果准确的话,请你总结方法,并说出如何判断对称轴的位置。
2.对称轴的画法
首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
3.画轴对称图形的对称轴举例
例1:画出以下图形的对称轴
例2:下面的虚线,哪些是图形的对称轴,哪些不是?
4.如果图形关于某一条直线对称,那么连结对称点的线段被对称轴垂直平分。
三、课堂练习
课本P88练习第1、2题。
四、课堂小结
要能熟练地画出轴对称图形的对称轴,知道如果图形关于某条直线对称,那么连结对称点的线段被对称轴垂直平分。
五、作业
课文P93习题10.2的第1、2题。
课后反思:
3.画轴对称图形
教学目的
1.使学生能够按要求作出简单平面图形经过一次对称后的图形。
2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。重点、难点重点:
重点:让学生识别轴对称图与画轴对称图形的对称轴。
难点:区别轴对称与轴对称图形两个不同的概念。
教学过程
一、复习巩固
1.什么是轴对称图形?
2.请你标出图中,A、B、C三点的对称点。
A
B
C
二、新课
如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢?
1.请同学们尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
(1)你可以通过什么方法来验证你画的是否正确?
(2)和其他同学比较一下,你的方法是最简单的吗?
在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形吗?
2.如图,已知点A和l直线,试画出点A关于直线l的对称点A′.请一位同学说说他的画法(其他同学可以补充):
l
A·
画好之后,你可以通过什么方法来验证一下A和 A′是否关于直线l对称?
例1.已知△ABC,直线l,画出△ABC关于直线l的对称图形。
(1)本题与上面的那些图比较有什么相同点和不同点?
(2)你能否从上面的那些图的画法中得到启示,帮助你解决本题?
A
B C
本题小结:如果图形是由直线、线段或射线组成时,那么画出它关于某一条直线对称的图形时,只要画出图形中的特殊点(如线段的中点,角的顶点等)的对称点,然后连结对称点,就可以画出关于这条直线的对称图形。
三、巩固练习
P90练习第1、2题。
四、小结
1.画轴对称图形,已知图形只是整个图形的一半。
2.因为整个图形是轴对称图形,所以要作的那一半与已知图形是
成轴对称的.
3.画轴对称图形的基础是画已知图形各点的轴对称点。
4.用尺规法画已知图中各点关于直线/的对称点,将对称点连结
得到对称线段,对称线段组成的的图形就是对称图形。
五、作业
P93习题10.2第3题。
课后反思:
4.设计轴对称图案
教学目的
1.使学生能设计简单的轴对称图案。
2.使学生能够欣赏现实生活中的轴对称图形。
重点、难点
重点:利用对称轴进行图案设计。
难点;寻找对称轴以及如何利用对称轴作轴对称图形。
一、复习巩固
1.如图(1),请画出△ABC的关于直线l对称的图形。
2.如图(2),等边△ABC是轴对称图形吗?如果是,它有几条对称轴?画画试试看。
A l A
B C B C
图(1) 图(2)
二、新课
在日常生活中,我们可以看到丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中有许多轴对称图形。请同学们欣赏P78四个装饰图案。
如图(3)是一个轴对称图形。
问:1.有多少条对称轴呢?
2.可以利用轴对称性来画出它吗?
请准备一张正方形纸片,按以下5个步骤一起来画。
(1)在正方形纸片上画出四条对称轴。
(2)在其中一个三角形中,如图,画出图形形状的基本线条。(注意:不同的线条最终会得到不同的图案,你可以自己设计线条,而不必和书上一样。)
(3)按照其中一条斜的对称轴画出(2)中图形的对称图形。
(4)按照另一条斜的对称轴画出(3)中图形的对称图形。
(5)按照水平(或垂直)对称画出(4)中图形的对称图形,即得到图(3)中的图。
在图案上涂上你喜欢的颜色,擦掉其他的线条,轴对称的图案就完成了。
三、练习巩固
P92练习1、2
四、小结
画轴对称图案,首先要画出对称轴,其次要画出图形形状的部分线条,然后根据对称性画出对称图形。
五、作业P93习题10.2第4题。
课后反思:
9.3等腰三角形
1.等腰三角形
第一课时 等腰三角形(1)
教学目的
1.使学生了解等腰三角形的有关概念,掌握等腰三角形的性质。
2.通过探索等腰三角形的性质,使学生进一步经历观察、实验、推理、交流等活动。
重点、难点
重点:等腰三角形等边对等角性质。
难点:通过操作,如何观察、分析、归纳得出等腰三角形性质。
教学过程
一、复习引入
1.让学生在练习本上画一个等腰三角形,标出字母,问什么样的三角形是等腰三角形?
△ABC中,如果有两边AB=AC,那么它是等腰三角形。
2.日常生活中,哪些物体具有等腰三角形的形象?
二、新课
1.指出△ABC的腰、顶角、底角。
相等的两边AB、AC都叫做腰,另外一边BC叫做底边,两腰的夹角∠BAC,叫做顶角,腰和底边的夹角∠ABC、∠ACB叫做底角。
2.实验。
现在请同学们做一张等腰三角形的半透明纸片,每个人的等腰三
角形的大小和形状可以不一样,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD,如图(2)所示,你能发现什么现象吗?请你尽可能多的写出结论。
可让学生有充分的时间观察、思考、交流,可能得到的结论:
(1)等腰三角形是轴对称图形
(2)∠B=∠C
(3)BD=CD,AD为底边上的中线。
(4)∠ADB=∠ADC=90°,AD为底边上的高线。
(5)∠BAD=∠CAD,AD为顶角平分线。
结论(2)用文字如何表述?
等腰三角形的两个底角相等(简写成“等边对等角”)。
结论(3)、(4)、(5)用一句话可以归结为什么?
等腰三角形的顶角平分线,底边上的高和底边上的中线互相重合 (简称“三线合一”)。
例l已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
本题较易,可由学生口述,教师板书解题过程。
引申:已知:在△ABC中,AB=AC,∠A=80°,求∠B和∠C的度数。
小结:在等腰三角形中,已知一个角,就可以求另外两个角。
三、练习巩固
P84 练习1、2、3
补充:
填空:在△ABC中,AB=AC,D在BC上,
1.如果AD⊥BC,那么∠BAD=∠______,BD=_______
2.如果∠BAD=∠CAD,那么AD⊥_____,BD=______
3.如果BD=CD,那么∠BAD=∠_______,AD⊥______
四、小结
本节课,我们学习了等腰三角形的性质:等腰三角形的两底角相等 (简写“等边对等角”);等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合(简称“三线合一”),它们对今后的学习十分重要,因此要牢记并能熟练应用。用数学语言表述如下:
1.△ABC中,如果AB=AC,那么∠B=∠C。
2.△ABC中,如果A月=AC,D在BC上,那么由条件(1)∠BAD=∠CAD,(2)AD⊥AC,(3)BD=CD中的任意一个都可以推出另外两个。
五、作业
P97练习第1题。
课后反思:
第二课时 等腰三角形(2)
教学目的
1.使学生熟练地运用等腰三角形的性质求等腰三角形内角的角度。
2.通过例题教学,帮助学生总结代数法求几何角度,线段长度的方法。
重点、难点
重点,等腰三角形的性质及其应用。
难点:简洁的逻辑推理。
教学过程
一、复习巩固
1.叙述等腰三角形的性质,它是怎么得到的?
等腰三角形的两个底角相等,也可以简称“等边对等角”。把等腰三角形对折,折叠两部分是互相重合的,即AB与AC重合,点B与点 C重合,线段BD与CD也重合,所以∠B=∠C。
等腰三角形的顶角平分线,底边上的中线和底边上的高线互相重合,简称“三线合一”。由于AD为等腰三角形的对称轴,所以BD= CD,AD为底边上的中线;∠BAD=∠CAD,AD为顶角平分线,∠ADB=∠ADC=90°,AD又为底边上的高,因此“三线合一”。
2.若等腰三角形的两边长为3和4,则其周长为多少?
二、新课
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。我们把三条边都相等的三角形叫做等边三角形。
等边三角形具有什么性质呢?
1.请同学们画一个等边三角形,用量角器量出各个内角的度数,并提出猜想。
2.你能否用已知的知识,通过推理得到你的猜想是正确的?
等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到∠A=∠B=C,又由∠A+∠B+∠C=180°,从而推出∠A=∠B=∠C=60°。
3.上面的条件和结论如何叙述?
等边三角形的各角都相等,并且每一个角都等于60°。
等边三角形是轴对称图形吗?如果是,有几条对称轴?
等边三角形也称为正三角形。
例1.在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求∠1和∠ADC的度数。
分析:由AB=AC,D为BC的中点,可知AB为 BC底边上的中线,由“三线合一”可知AD是△ABC的顶角平分线,底边上的高,从而∠ADC=90°,∠l=∠BAC,由∠C=∠B=30°,∠BAC可求,所以∠1可求。
问题1:本题若将D是BC边上的中点这一条件改为AD为等腰三角形顶角平分线或底边BC上的高线,其它条件不变,计算的结果是否一样?
问题2:求∠1是否还有其它方法?
三、练习巩固
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合()
b.有一个角是60°的等腰三角形,其它两个内角也为60°()
2.如图(2),在△ABC中,已知AB=AC,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。
四、小结
由等腰三角形的性质可以推出等边三角形的各角相等,且都为60°。“三线合一”性质在实际应用中,只要推出其中一个结论成立,其他两个结论一样成立,所以关键是寻找其中一个结论成立的条件。
五、作业
1.P97练习第2、3题。
补充:如图(3),△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
课后反思:
2.等腰三角形的识别
教学目的
1.通过探索一个三角形是等腰三角形的条件,培养学生的探索能力。
2.能利用一个三角形是等腰三角形的条件,正确判断某个三角形是否为等腰三角形。
重点、难点
重点:让学生掌握一个三角形是等腰三角形的条件和正确应用。
难点:一个三角形是等腰三角形的条件的正确文字叙述。
教学过程
一、复习引入
等腰三角形具有哪些性质?
等腰三角形的两底角相等,底边上的高、中线及顶角平分线“三线合一”。
二、新课
对于一个三角形,怎样识别它是不是等腰三角形呢?我们已经知道的方法是看它是否有两条边相等。这一节,我们再学习另一种识别方法。
我们已学过,等腰三角形的两个底角相等,反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
为了回答这个问题,请同学们分别拿出一张半透明纸,做一个实验,按以下方法进行操作:
1.在半透明纸上画一个线段BC。
2.以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的角,两角终边的交点为A。
3.用刻度尺找出BC的中点D,连接AD,然后沿AD对折。
问题1:AB与AC是否重合?
问题2:本实验的条件与结论如何用文字语言加以叙述?
如果一个三角形有两个角相等,那么这两个角所对的边也相等,简写成“等角对等边”。
也就是说,如果一个三角形中有两个角相等,那么它就是等腰三角形。一个三角形是等腰三角形的条件,可以用来判定一个三角形是否为等腰三角形。
例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?
问题3:三个角都是60°的三角形是等边三角形吗?你能说明理由吗?
等腰直角三角形:顶角是直角的等腰三角形是等腰直角三角形,如图所示。
问题4:你能说出等腰直角三角形各角的大小吗?
问题5:请你画一个等腰直角三角形,使∠C=90°,CD是底边上的高,数一数图中共有几个等腰直角三角形?
三、练习巩固
P99练习l、2、3题。
四、小结
这节课,,我们学习了一个三角形是等腰三角形的条件:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”),此条件可以做为判断一个三角形是等腰三角形的依据。因此,要牢记并能熟练应用它。
五、作业
1.P99习题第4、5题。
课后反思:
小结与复习
教学目的
1.使学生对整章的学习内容做一回顾,系统地把握全章的知识要点和基本技能。
2.通过例题和练习,使学生能较好地运用本章知识和技能解决有关问题。
重点、难点
判断图形是否是轴对称图形,线段的垂直平分线、角平分线的性质、等腰三角形的性质和判定及其应用是教学重点,而灵活运用上述性质解决问题、轴对称图案的设计是教学难点。
教学过程
一、知识回顾
问题1:轴对称图形的定义是什么?
它是判断图形是否是轴对称图形的依据。
问题2:是否会画轴对称图形的对称轴?
找出轴对称图形的任一组对称点,连结对称点,画对称点所连线段的垂直平分线,即得到该图形对称轴。
问题3:轴对称图形对称点的连线与对称轴有什么关系?
轴对称图形对称点的连线被对称轴垂直平分。
问题4:线段垂直平分线、角平分线具有什么性质?
线段垂直平分线上的点到线段两端的距离相等;角平分线上的点到角两边的距离相等。
问题5:等腰三角形有什么性质?
等腰三角形底边的中线、高线、顶角的平分线互相重合,等腰三角形的两个底角相等(等边对等角),等边三角形的三个角都等于60°。
问题6:如何判断三角形是等腰三角形?等边三角形?
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);有两个角是60°的三角形是等边三角形,有一个角是60°的等腰三角形是等边三角形。
二、例题
1.下列图案是轴对称图形的有( )
A.1个D.2个C.3个D.4个
2.如右图所示,已知,OC平分∠AOB,D是OC上一点,DE⊥OA,DF⊥OB,垂足为E、F点,那么
(1)∠DEF与∠DFE相等吗?为什么?
(2)OE与OF相等吗?为什么?
三、巩固练习
如右图所示,已知AB=AC,DE垂直平分AB交AC、AB于D、E两点,若AB=12cm,BC=l0cm,∠A=49°14′54″.求△BCD的周长和∠DBC度数。
四、课堂小结
通过本节课复习,同学们应掌握本章知识和技能,并运用所学知识和技能解决问题,
五、作业
课后反思:
第10章 平移与旋转
§10.2 平 移
教学目标:
知识与技能目标:
1.通过具体实例认识图形的平移变换,探索它的基本性质. 2.能按要求作出简单的平面图形平移后的图形.3、要明确平面图形的平移变换,不少平面图案都可以看作是由其中的某一部分,沿着上下或左右的方向,平移若干次而成的。
过程与方法目标:
通过具体实例认识图形的平移变换,通过现实生活中各种丰富的实例,让学生体会图形的平移现象,让学生通过各种图形的平移,体验感受图形平移的主要因素是移动的方向和移动的距离. 探索它的基本性质。
情感与态度目标:
认识和欣赏这些图形的平移变换在现实生活中的应用,体会到数学与实际生活的密切联系,认识到数学的价值。
教学重、难点与关键:
重点:平移的基本内涵与基本性质
难点:发现原图形与平移后图形间的关系。
教学时间安排:3教时
§10.2.1图形的平移
教学程序设计:
一、创设问题情景
1、投影:引言及插图。
2、回忆游乐园内的一些项目,如:旋转木马、荡秋千、小火车、滑梯……
3、观察图片中传送带上的电视机与手扶电梯上的人,回答以下问题:
(1)传送带上每台电视机做什么运动?手扶电梯上的人呢?
(2)传送带上的电视机的形状、大小在运动前后是否发生了改变?手扶电梯上的人呢?
(3)在传送带上,如果电视机的某一按键向前移动了80cm,那么电视机的其他部位向什么方向移动?移动了多少距离?
(4)如果把移动前后的同一台电视机的屏幕分别记为四边形ABCD和四边形EFGH(课件演示),那么四边形ABCD与四边形EFGH的形状、大小是否相同?
4、图案欣赏(课件演示)
二、探究新知
(一)、平移的概念
1.平移的概念:
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移不改变图形的形状和大小。
2.它由什么要素决定?
3.对应点、对应线段、对应角
反馈训练应用提高
P67页练习1、2
(二)、平移的基本性质:
1、想一想:
(1)在上图中,线段AE,BF,CG,DH有怎样的位置关系?
(2)图中每对对应线段之间有怎样的位置关系?
(3)图中有哪些相等的线段、相等的角?
2、归纳平移的基本性质:
经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
3、做一做:
如图所示,△ABE沿射线XY的方向
平移一定距离后成为△CDF.找出图中存在
的平行且相等的三条线段和一组全等三角形.
反馈训练应用提高
1、练习:P68页练习3
2思考:图中的四个小三角形都是等边三角形,
边长为2cm,能通过平移△ABC得到其它
三角形吗?若能,请画出平移的方向,并说出平移的距离.
三、小结提高
1、回顾本节课的活动过程:观察——分析——探索——概括。
2、本节课学到了哪些知识和方法?
四、布置作业
教材第71页习题1、2。
五、反思
§10.2.2 平移的特征
教学程序设计:
一、创设问题情景
上节课你学到了什么?举例
二、探究新知
投影:例1如图11.1.8(1),△ABC经过平移到△A′B′C′的位置,指出平移的方向,并量出平移的距离。
投影:试一试
在如图11.1.9的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A″B″C″。△A″B″C″是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
投影:做一做
如图11.1.10,在纸上画△ABC和两条平行的对称轴m、n。画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″。
观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
三、反馈训练应用提高
1.平移方格纸中的图形(如图),使点A平移到点A′处,画出平移后的图形。
2.图案欣赏(提高认识)
四、小结提高
1、回顾本节课的活动过程:观察——分析——探索——概括。
2、本节课学到了哪些知识和方法?
五、布置作业
教材第70页练习1、2、3。
六、反思
§10.2图形的平移练习
教学程序设计:
一、创设问题情景
前面你学到了什么?举例
二、探究新知
例:图中的四个小三角形都是等边三角形,边长为2cm,能通过平移△ABC得到其它三角形吗?若能,请画出平移的方向,并说出平移的距离.
随堂练习:(投影)
1、填空:
(1)将线段AB向右平移3cm得到线段CD,如果AB=5 cm,则CD= cm.
(2)将∠ABC向上平移10cm得到∠EFG,如果∠ABC=52°,则∠EFG= °,BF= cm.
(3)将面积为30cm2的等腰直角三角形ABC向下平移20cm,得到△MNP,则△MNP是 三角形,它的面积是 cm2.
2、图中小船经过平移到了新的位置,你发现少了什么?请补上.
3、如图1,在四边形ABCD中,AD∥BC,AB=CD,AD<BC,要探究∠B与∠C的关系,可以采用平移的方法(如图2、3)。请你分别说明图形的形成过程,同时判断∠B与∠C的关系并叙述理由,你还有其他方法吗?请在图1中画出你的方案。
三、小结提高
1、回顾本节课的活动过程:
2、本节课学到了哪些知识和方法?
四、布置作业
教材第71页习题3、4。
五、反思
§10.3 旋 转
教学目标:
知识与技能目标:1.认识图形的旋转变换,掌握它的基本性质. 2.认识旋转对称图形,并能够按要求作出简单的平面图形旋转后的图形.3.培养学生创造图案的设计能力
过程与方法目标:
1.、通过具体实例认识图形的旋转变换,探索它的基本性质.引导学生,探索发现原图形经过旋转后的对应点、对应线段之间的位置关系与数量关系.体验感受图形旋转的主要因素是旋转中心和旋转的角度,从而体会到图形在旋转过程中,图形中的每一点都绕着旋转中转动了相同的角度2.认识旋转对称图形,理解旋转对称图形的概念,重视对学生自行设计旋转对称图形的能力的培养,并能够按要求作出简单的平面图形旋转后的图形.
情感与态度目标:
认识和欣赏这些图形的旋转变换在现实生活中的应用,体会到数学与实际生活的密切联系,经历对生活中与旋转现象有关的图形进行观察、分析、欣赏、交流等活动,发展初步的审美能力,增强对图形欣赏的意识。
教学重、难点:
重点:旋转变换的基本性质,并能根据性质作出简单的平面图形旋转后的图形。
难点:旋转变换的基本性质的探索,作出简单的平面图形旋转后的图形。
§10.3.1 图形的旋转
教学程序设计:
一、创设问题情景
1.课件演示,旋转而动产生的奇妙画面。2.你能自己举出日常生活中的一些事例吗?
二、探究新知1
1.观察图形找出这些图形的共同特征:
2.概念:旋转、旋转中心
三、探究新知2
1.做一做
用一张半透明的薄纸,覆盖在画有任意△AOB的纸上,在薄纸上画出与△AOB重合的一个三角形。然后用一枚图钉在点O处固定,将薄纸绕着图钉(即点O)转动一个角度45,薄纸上的三角形就旋转到了新的位置,标上A′、O′、B′,我们可以认为△AOB旋转45后到了上△A′O′B′。在这样的旋转过程中,你发现了什么?
四、探究新知3
做一做
如图11.2.5,如果旋转中心在△ABC的外面点O处,转动60,将整个△ABC旋转到△A′B′C′的位置。那么这两个三角形的顶点、边与角是如何对应的呢?
五、探究新知4
1、如图11.2.6,△ABC是等边三角形,D是BC上一点,
△ABD经过旋转后到达△ACE的位置。
旋转中心是哪一点?
旋转了多少度?
如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
2、如图11.2.7(1),点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转90呢?
六、小结提高
说说“旋转”的概念,旋转的等量关系。
说说描述“旋转”的过程要注意哪几方面?
七、布置作业
课本P74页练习2、3
八、反思
§10.3.2 旋转的特征
教学程序设计:
一、创设问题情景
回顾旋转的概念
二、探究新知1
探索
观察下面两个图形,你能发现有哪些线段相等?有哪些角相等?
你认为图形旋转的特征是什么?
教师组织学生分组讨论。
练习
1.确定图形中的旋转中心,指出这一图形是由哪个基本图形旋转多少度、旋转几次而生成的(不计颜色)。
2.画出△ABC绕点C逆时针旋转90后的图形
三、小结提高
说说“旋转”的概念,旋转的等量关系。
说说描述“旋转”的过程要注意哪几方面?
四、布置作业
1、画出所给图形绕点O顺时针旋转90后的图形。旋转几次后可以与原图形重合?
2、课本P76页练习1、2、3
五、反思
§10.3.3 旋转对称图形
教学程序设计:
一、创设问题情景
1.回顾旋转的概念
2.如图,画出ΔABC绕O点顺时针旋转60°的图形ΔA’B’C’.
二、探究新知
实验1、画出正方形绕对角线的交点顺时针旋转90°的图形.观察旋转后的图形与原正方形有何关系?
实验2.如图11.2.8所示,电扇的叶片转动120、螺旋桨转动180后,都能与自身重合。
你能再举出一些这样的实例吗?
实验3、用一张半透明的薄纸,覆盖在如11.2.9所示的图形上,在薄纸上画这个图形,使它与如图11.2.9所示的图形重合。然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转,观察旋转多少度(小于周角)后,薄纸上的图形能与原图形再一次重合。
问题:前面3个实验有什么共同的特性?
概念:
旋转对称图形:绕着某一点旋转一定角度(小于周角)后能与自身重合的图形.
三、操作训练
操作1:用类似上述的操作方法对如图11.2.10所示的图形进行探索,看看它是不是旋转对称图形?想一想旋转中心在何处?该图形需要旋转多少度后,能与自身重合?该图形是轴对称图形吗?
操作2:图11.2.11所示的图形是轴对称图形,用类似上述的操作方法对图11.2.11所示的图形进行探索,它能通过旋转与自身重合吗?
1.找找看,下面图形中有几匹马?它们的位置关系如何?
2.如图所示的图形绕哪一点旋转多少度后能与自身重合?
3.如图,画出ΔABC绕O点逆时针旋转60°的图形ΔA’B’C’.
四、小结提高
说说“旋转对称”的概念。
说说描述“旋转对称”的过程要注意哪几方面?
想一想:
1、正方形旋转180°后能与自身重合吗?还能旋转几度与自身重合?
2、正五边形、正六边形、正七边形……最小旋转多少度能与自身重合?
五、布置作业
P78页练习1、2、3、4
六、反思
§10.4 中心对称
教学目标:
知识与技能目标:
1、通过具体实例认识中心对称,探索它的基本性质,理解: “连结对称点的线段都经过对称中心,并且被对称中心平分”, “中心对称是旋转角度为180°的特殊的旋转对称” 2、发展学生的合情推理能力,进一步培养学生的数学说理的习惯与能力.
过程与方法目标:
1、让学生自己通过丰富的具体图形认识中心对称与中心对称图形,探索它的基本性质,体会中心对称图形是旋转角度为 180°的特殊的旋转对称图形2、在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,进一步培养学生的数学说理的习惯与能力.
情感与态度目标:
认识和欣赏这些特殊的旋转变换在现实生活中的应用,体会到数学与实际生活的密切联系,经历对生活中与旋转现象有关的图形进行观察、分析、欣赏、交流等活动,发展初步的审美能力,增强对图形欣赏的意识。
教学重、难点与关键:
重点:中心对称的基本性质,并能根据性质作出简单的平面图形中心对称图形。
难点:中心对称的基本性质的探索,作出简单的平面图形中心对称图形。
教时安排:3教时
§10.4中心对称 第一课时
教学程序设计:
一、创设问题情景
课件演示如图11.3.1所示的三个图形都是旋转对称图形。
1、上面图形中哪个图形旋转180°能与自身图形重合?
2、你能自己举出日常生活中旋转180°的一些事例吗?
二、探究新知1
1、一个图形绕着中心点旋转180后能与自身重合,我们就把这种图形叫做中心对称图形, 这个中心点叫做对称中心。
你能举一些中心对称图形吗?他们的对称中心在哪里?
2、把一个图形绕着某一点旋转180,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点
如图11.3.2所示,△ABC与△ADE就是成中心对称的两个三角形,点A是对称中心,
三、探究新知2
在图11.3.3中,△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
归纳板书:
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
反过来,如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成中心对称。
四、探究新知3
例:如图11.3.4(1),已知△ABC和点O,画出△DEF,使△DEF和△ABC关于
点O成中心对称。
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D;
(2)同样画出点B和点C的对称点E和F;
(3)顺次连结DE、EF、FD。
如图11.3.4(2),△DEF即为所求的三角形。
训练应用提高
1、课本P81页练习1、2
2、P82页 读一读
五、小结提高
说说中心对称和中心对称图形的区别和联系。
中心对称有什么基本的性质?
六、布置作业
课本P84页习题1、2
七、反思
§10.4中心对称 第二课时
教学程序设计:
一、创设问题情景
回顾中心对称、中心对称图形及其基本性质
二、探究新知1
1、点A和O,求作A关于O点对称的图形。
2、已知线段AB和点O,求作AB关于点O对称的图形。
3、已知三角形ABC和点O,求作三角形ABC关于点O对称的图形。
4、已知四边形ABCD和点O,求作四边形ABCD关于点O对称的图形。
三、探究新知2
试一试:如图11.3.5所示的两个图形成中心对称,你能找到对称中心吗?
说说你这样画的理由。
反馈训练应用提高
课本P21页1
四、小结提高
说说中心对称和中心对称图形的区别和联系。中心对称有什么基本的性质?
五、布置作业
课本P83页练习1、2
六、反思
§10.4中心对称复习 第三课时
教学程序设计:
一、创设问题情景
回顾中心对称、中心对称图形及其基本性质。
回顾轴对称、轴对称图形及其基本性质。并完成
1、点A和直线l,求作A关于l对称的图形。
2、已知线段AB和点l,求作AB关于点l对称的图形。
3、已知三角形ABC和点l,求作三角形ABC关于点l对称的图形。
二、探究新知1
做一做
如图11.3.6,在纸上画△ABC、点P,以及与△ABC关于点P成中心对称的三角形△A″B″C″。
过点P任意画一条直线,画出△ABC关于此直线对称的△A′B′C′,如图11.3.7。
观察△A′B′C′和△A″B″C″,这两个三角形对称吗?画出使这两个三角形成轴对称的对称轴,你发现了什么?
两次翻折(对称轴互相垂直)与中心对称的关系:
如果对称轴互相垂直,那么两次翻折就相当于一次中心对称,且两条对称轴的垂足为对称中心.
反馈训练应用提高
1、阅读材料:古建筑中的旋转对称
―――从敦煌洞窟到欧洲教堂
2、如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于直线y对称的△A″B″C″,△A″B″C″与△ABC是否关于点O成中心对称?
三、小结提高
两次翻折(对称轴互相垂直)与中心对称的关系。
四、布置作业
课本P84页习题1、2、3、4
五、反思
§10.5 图形的全等
教学目标:
1、通过问题的解决,图形的实例,体验全等图形的形成,体会到如何直观地判别两个图形是全等图形,通过动手实验进一步掌握全等图形的概念,全等多边形的特征;
2、了解全等多边形、对应边、对应顶点、对应角的概念;
3、培养学生动手试验的能力与习惯,树立实践出真知的观念。
重点难点:
1、难点:全等多边形的概念和特征;2、重点:全等多边形的对应元素的确定。
教学过程:
一、复习引入
1、问题1、请同学们观察老师手上的两张照片(1寸和2寸的照片),用你们学过的知识来回答观察到什么?(两张照片是相似图形,其相似比是)
2、请几位同学说说相似图形的特征与识别。
3、问题2:请同学们再观察老师手上的两张照片(都是两寸的照片),也用数学的知识说说观察到什么?(两个图形的形状、大小也一样,即相似屁的相似图形)
本节开始,我们就来探索、研究这种图----§24.1图形的全等
二、新授
1、全等图形
试一试:(课本P85)你能找到几对形状相同、大小一样的图形吗?
(两对:(2)和(4)、(3)和(6))
问:如何判断两个图形的大小和形状是否完全相同的?
(学生各抒已见,给予表扬鼓励)
问:发挥你们的想像,两个大小和形状完全相同的图形叠合在一起,是否完全重合。动手试试。
(可用你们带来的工具) (完全重合)
问:通过动手试验,你得到了什么结论?
(判断两个图形的大小和形状是否完全相同,可以把两个图形叠合在一起,看是否完全重合。)
我们把能够完全重合的两个图形叫做全等形。
练习:(1)课本试一试的图中的 就是全等形。
(2)课本 P87 练习
2、全等多边形及对应顶点、对应边、对应角的概念。
问题3:观察老师的演示(用大小一样的照片,演示翻折、旋转、平移的运动),请问:老师把这些图
形进行哪些运动?形状、大小发生了改变吗?从中你得到了什么结论?
学生发表看法。
老师总结:我们把图形的翻折、旋转、平移称是图形的三种基本的运动,图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的。反过来,两个全等的图形经过这样的运动一定能够重合。
完成课本P85 思考。
由学生的回答中引出:
全等多边形:能够完全重合的两个多边形。
对应顶点:两个全等的多边形,经过运动而重合,相互重合的顶点。
对应边:相互重合的边。
对应角:相互重合的角。
如图24.1.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”)(请同学们试指出两个图形的对应顶点、对应边和对应角。
练习:指出下列各图中的全等三角形,指出对应顶点、对应边、对应角。
由学生的练习中,引导学生讨论:如何记作全等形,能很快地指出对应边、对应角。可以小组讨论交流找出你认为较为科学、合理的方法。
(对应位置的字母,表示两个图形的对应顶点,比如△ABC≌△,A与,B与,C与是对应顶点,对应顶点决定的边是全等三角形的对应边。)
练习:已知;四边形ABCDE≌四边形EFGH,写出它们所有的对应边及对应角。
3、全等多边形的特征、识别。
问题4:依据上面的分析,全等多边形有哪些特征呢?
全等多边形的对应边、对应角分别相等。
如五边形ABCDE≌五边形A′B′C′D′E′
对应角相等:, ,,
对应边相等:,,,
,
实际上这也是我们识别全等多边形的方法,即_______________的两个多边形全等。
例:如图(1)△ABC≌△DEF,你得到 ;
(2) ,可以得到△ABC≌△DEF。
练习:已知如图24.1.4△ABC≌△DEF,△ABC的周长是,,,求△DEF中,边DF的长度。
三、小结
对过本节学习,谈谈你的体会,收获,疑惑。
四、作业
P87习题 1、2
10、1生活中的轴对称
第一课时 生活中的轴对称
教学目的
1.通过展示轴对称图形的图片,使学生初步认识轴对称图形;
2.通过试验,归纳出轴对称图形概念,能用概念判断一个图形是否是轴对称图形;
3.培养学生的动手试验能力、归纳能力和语言表述能力。
重点、难点
轴对称图形的概念是教学重点,判断图形是否是轴对称图形既是教学重点又是教学难点。
教具准备
一些关于轴对称的图片、半透明纸张。
教学过程
一、引入
1.展示图片,认识一些轴对称图形。
自远古以来,对称形式被认为是和谐美丽、并且真实的,不论是在自然界中还是建筑里,甚至最普通的日常生活用品中,对称的形式随处可见,青山倒映在水中,这是令人难忘的对称景象。同学们可以想象,当你放学回家,落日、晚霞、还有远处的青山倒映在平静的水中,这样如诗如画的景致怎能不令人难忘,
2.课上展开讨论,列举出一些现实生活中有关轴对称的物体和建筑物。
二、新课
1.试验
把一张半透明纸对折,然后从折叠处剪出一个图形,展开后会是一个什么样的图形?
由教师先示范剪出一个图形,而后由同学们自由发挥想象,剪出图案。
2.由展示的图片和同学们剪出的图案归纳轴对称图形的概念。
从同学们剪出的图案和展示的图片来看,这些图形如果沿着某条直线对折,对折的两部分是完全重合的,这样的图形称为轴对称图形这条直线叫做这个图形的对称轴。
三、练习
1.要求同学们找出所剪的图案的对称轴,并且用直尺把它画出来。
2.结合展示图片,让同学们找对称轴,并使同学们知道有的轴对称图形不止一条对称轴。3.给每位同学发一张半透明的画有如右图所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有几条对称轴。
四、课堂小结
本节课认识了什么样的图形是轴对称图形,这些图形都有共同的特点,就是沿着某条直线对折,直线两旁的图形完全重合,这条直线称为这个图形的对称轴。值得同学们注意的是,有的轴对称图形的对称轴不止一条,例如,练习第3题中的星形图就有六条对称轴。
五、作业
1.第82页练习第1、2题。
2.第82页习题10.1练习第1、2题
课后反思:
第二课时 生活中的轴对称
教学目的
使学生进一步认识轴对称图形,通过动手实验,掌握关于某条直线成轴对称的两个图形的对应线段相等、对应角相等;理解轴对称图形和两个图形成轴对称这两个概念的区别与联系。
重点、难点
重点:轴对称图形的对应线段相等、对应角相等。
难点:两个图形成轴对称与轴对称图形两个概念的区别与联系。
一、复习、评讲
1.复习轴对称图形的定义。
2.评讲上节课的作业,使学生进一步掌握判断一个图形是否是轴对称图形。
二、新课
1.什么是两个图形成轴对称?
试验:发给每位同学右边两个图形的纸张,把纸张沿着虚线折叠,观察对折后的左边部分和右边部分是否完全重合?
像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两图形重合时互相重合的点)叫做对称点。
练习:在上图的(2)中,把A、B、C的对称点标出来。
试验:在纸上滴上墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称?它的对称轴是哪一条?把它画出来。
2.轴对称图形(或关于某条直线成对称的两个图形)沿对称轴对折后的两部分完全重合,所以它的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等。
3.轴对称图形与两个图形成轴对称的区别与联系.
如图(1),如果沿着虚线对折,直线两旁的部分会完全重合,那么这个图形就是轴对称图形;若把这个图形看成是左右两部分,则这两个图形就是关于虚线这条直线成轴对称。
如图(2),如果沿着虚线折叠,右边的图形会与左边的图形完全重合,那么就说这两个图形关于虚线这条直线成轴对称,若把(2)中的左右两个四边形看成是一个整体的图形,那么这个整体的图形是轴对称图形。
因此,轴对称图形和两个图形成轴对称的本质是相同的,只是怎么看图形的问题。
三、巩固练习
1.下面哪些选项的右边图形与左边图形成轴对称?
2.如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等?哪些线段相等?
四、课堂小结成轴对称的两个图形是完全重合的,因此,它们的对应线段相等,对应角相等;知道轴对称和轴对称图形的区别与联系。
五、作业
课本P82习题第3、4题。
课后反思:
10.2 轴对称的认识
1.简单的轴对称图形
第一课时 线段的垂直平分线
教学目的
通过动手试验,使学生知道线段是轴对称图形,掌握线段的垂直子分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。
重点、难点
重点:线段垂直平分线上的点到线段两端的距离相等。
难点:运用线段垂直平分线性质解决问题。
教学过程
一、复习引入
1.轴对称图形的定义是什么?
2.线段是轴对称图形吗?它的两个端点是否关于某条直线成轴对称?
二、新课
1.认识线段是轴对称图形,引出线段垂直平分线的定义。
试验:按以下方法,看看线段是否是轴对称图形?
在半透明纸上画出线段AB和它和中点O,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合?
显然,线段OA和OB互相重合,因此,线段是轴对称图形。那么,线段的对称轴是哪一条呢?
线段垂直平分线的定义:垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线。如上图的直线 CD就是线段AB的垂直平分线。
2.线段垂直平分线上的点到线段两端的距离相等。
在以上试验的基础上,同学们在直线CD上任意取一点M,连结 MA、MB,而后沿着直线CD折叠,观察MA和MB是否重合?再取一点试试,观察PA和PB是否重合?待同学们实验完毕,引导同学们归纳线段垂直平分线的性质。
线段垂直平分线上的点到线段两端的距离相等。
3.线段垂直平分线性质的应用举例。
例1.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
分析:要求△BCE的周长,需知道BE、CE、BC的长度,从题目给出的条件来看,BE、BC的长度已经知道,而正点是线段BC的垂直平分线上的点,所以CE=BE,从而问题得到解决。
例2.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗?为什么?
三、课堂练习
课本P85练习第1、2题
四、课堂小结
线段垂直平分线的性质及其运用是本节课的重点,应用其性质我们可以证明两条线段相等。
作业
1、如图1,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
图1 图2
2.如图2,△BAC=120°,∠C=30°,DE是线段AC的垂直平分线,求:∠BAD的度数。
课后反思:
第二课时 角平分线
教学目的
使学生知道角是轴对称图形,对称轴是角平分线所在的直线,掌握角平分线的性质,并能运用它解决相关问题。
重点、难点
重点:角平分线上的点到角两边的距离相等。
难点:运用角平分线性质解决问题。
教学过程
一、复习引入
1.点到直线的距离的定义是什么?
2.角是轴对称图形吗?对称轴是哪一条直线?
二、新课
1.认识角是轴对称图形,知道角平分线所在的直线是它的对称轴。
试验:按以下方法试验,使同学认识角是轴对称图形。
在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM。
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线。
2.角平分线上的点到角两边的距离相等。
在以上试验的基础上,同学们在射线OM上任取一点P,过P点分别作OA和OB的垂线PC和PD,而后沿着OM折叠,观察PC和 PD是否重合?再取一点,按上述同样的方法试验,待同学们试验完毕,引导同学归纳角平分线的性质。
角平分线上的点到角两边的距离相等。
3.角平分线性质应用举例
例1.如下图(1)所示,在△ABC中,∠C= 90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD和3DC是什么关系?为什么?
图(1) 图(2)
例2.如上图(2),BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,P=3cm,求 P点到直线AB的距离。
三、课堂练习
(课本P86第3、4题)
四、课堂小结
角是轴对称图形,对称轴是角平分线所在的直线。运用角平分线性质可以说明两条线段相等。
五、作业
1.如图3,AD平分∠BAC,∠C=90°,DE⊥ AB,那么(1)DE和DC相等吗?为什么? (2)AE和AC相等吗?为什么?
2.如图4,在△ABC中,用直尺、量角器画∠A、∠B、∠C的平分线,看看三条角平分线有什么关系?
图3 图4
课后反思:
2.画图形的对称轴
教学目的
使学生掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并请熟练画出轴对称图形的对称轴。
重点、难点
重点:画轴对称图形的对称轴。
难点:归纳总结画轴对称图形对称轴的方法。
教学过程
一、复习
1.轴对称图形以及它的对称点是怎么定义的?
2.看以下两个图形是否是轴对称图形?你能否画出它的对称轴?
二、新课
1.试着画出下边两个图形的对称轴。
用折叠的方法检验所画的对称轴是否准确,如果准确的话,请你总结方法,并说出如何判断对称轴的位置。
2.对称轴的画法
首先找出轴对称图形的任意一组对称点,连结对称点,其次画对称点所连线段的垂直平分线,就得到该图形的对称轴。
3.画轴对称图形的对称轴举例
例1:画出以下图形的对称轴
例2:下面的虚线,哪些是图形的对称轴,哪些不是?
4.如果图形关于某一条直线对称,那么连结对称点的线段被对称轴垂直平分。
三、课堂练习
课本P88练习第1、2题。
四、课堂小结
要能熟练地画出轴对称图形的对称轴,知道如果图形关于某条直线对称,那么连结对称点的线段被对称轴垂直平分。
五、作业
课文P93习题10.2的第1、2题。
课后反思:
3.画轴对称图形
教学目的
1.使学生能够按要求作出简单平面图形经过一次对称后的图形。
2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。重点、难点重点:
重点:让学生识别轴对称图与画轴对称图形的对称轴。
难点:区别轴对称与轴对称图形两个不同的概念。
教学过程
一、复习巩固
1.什么是轴对称图形?
2.请你标出图中,A、B、C三点的对称点。
A
B
C
二、新课
如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢?
1.请同学们尝试解决以下问题;
如图(1),实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
(1)你可以通过什么方法来验证你画的是否正确?
(2)和其他同学比较一下,你的方法是最简单的吗?
在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形吗?
2.如图,已知点A和l直线,试画出点A关于直线l的对称点A′.请一位同学说说他的画法(其他同学可以补充):
l
A·
画好之后,你可以通过什么方法来验证一下A和 A′是否关于直线l对称?
例1.已知△ABC,直线l,画出△ABC关于直线l的对称图形。
(1)本题与上面的那些图比较有什么相同点和不同点?
(2)你能否从上面的那些图的画法中得到启示,帮助你解决本题?
A
B C
本题小结:如果图形是由直线、线段或射线组成时,那么画出它关于某一条直线对称的图形时,只要画出图形中的特殊点(如线段的中点,角的顶点等)的对称点,然后连结对称点,就可以画出关于这条直线的对称图形。
三、巩固练习
P90练习第1、2题。
四、小结
1.画轴对称图形,已知图形只是整个图形的一半。
2.因为整个图形是轴对称图形,所以要作的那一半与已知图形是
成轴对称的.
3.画轴对称图形的基础是画已知图形各点的轴对称点。
4.用尺规法画已知图中各点关于直线/的对称点,将对称点连结
得到对称线段,对称线段组成的的图形就是对称图形。
五、作业
P93习题10.2第3题。
课后反思:
4.设计轴对称图案
教学目的
1.使学生能设计简单的轴对称图案。
2.使学生能够欣赏现实生活中的轴对称图形。
重点、难点
重点:利用对称轴进行图案设计。
难点;寻找对称轴以及如何利用对称轴作轴对称图形。
一、复习巩固
1.如图(1),请画出△ABC的关于直线l对称的图形。
2.如图(2),等边△ABC是轴对称图形吗?如果是,它有几条对称轴?画画试试看。
A l A
B C B C
图(1) 图(2)
二、新课
在日常生活中,我们可以看到丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中有许多轴对称图形。请同学们欣赏P78四个装饰图案。
如图(3)是一个轴对称图形。
问:1.有多少条对称轴呢?
2.可以利用轴对称性来画出它吗?
请准备一张正方形纸片,按以下5个步骤一起来画。
(1)在正方形纸片上画出四条对称轴。
(2)在其中一个三角形中,如图,画出图形形状的基本线条。(注意:不同的线条最终会得到不同的图案,你可以自己设计线条,而不必和书上一样。)
(3)按照其中一条斜的对称轴画出(2)中图形的对称图形。
(4)按照另一条斜的对称轴画出(3)中图形的对称图形。
(5)按照水平(或垂直)对称画出(4)中图形的对称图形,即得到图(3)中的图。
在图案上涂上你喜欢的颜色,擦掉其他的线条,轴对称的图案就完成了。
三、练习巩固
P92练习1、2
四、小结
画轴对称图案,首先要画出对称轴,其次要画出图形形状的部分线条,然后根据对称性画出对称图形。
五、作业P93习题10.2第4题。
课后反思:
9.3等腰三角形
1.等腰三角形
第一课时 等腰三角形(1)
教学目的
1.使学生了解等腰三角形的有关概念,掌握等腰三角形的性质。
2.通过探索等腰三角形的性质,使学生进一步经历观察、实验、推理、交流等活动。
重点、难点
重点:等腰三角形等边对等角性质。
难点:通过操作,如何观察、分析、归纳得出等腰三角形性质。
教学过程
一、复习引入
1.让学生在练习本上画一个等腰三角形,标出字母,问什么样的三角形是等腰三角形?
△ABC中,如果有两边AB=AC,那么它是等腰三角形。
2.日常生活中,哪些物体具有等腰三角形的形象?
二、新课
1.指出△ABC的腰、顶角、底角。
相等的两边AB、AC都叫做腰,另外一边BC叫做底边,两腰的夹角∠BAC,叫做顶角,腰和底边的夹角∠ABC、∠ACB叫做底角。
2.实验。
现在请同学们做一张等腰三角形的半透明纸片,每个人的等腰三
角形的大小和形状可以不一样,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD,如图(2)所示,你能发现什么现象吗?请你尽可能多的写出结论。
可让学生有充分的时间观察、思考、交流,可能得到的结论:
(1)等腰三角形是轴对称图形
(2)∠B=∠C
(3)BD=CD,AD为底边上的中线。
(4)∠ADB=∠ADC=90°,AD为底边上的高线。
(5)∠BAD=∠CAD,AD为顶角平分线。
结论(2)用文字如何表述?
等腰三角形的两个底角相等(简写成“等边对等角”)。
结论(3)、(4)、(5)用一句话可以归结为什么?
等腰三角形的顶角平分线,底边上的高和底边上的中线互相重合 (简称“三线合一”)。
例l已知:在△ABC中,AB=AC,∠B=80°,求∠C和∠A的度数。
本题较易,可由学生口述,教师板书解题过程。
引申:已知:在△ABC中,AB=AC,∠A=80°,求∠B和∠C的度数。
小结:在等腰三角形中,已知一个角,就可以求另外两个角。
三、练习巩固
P84 练习1、2、3
补充:
填空:在△ABC中,AB=AC,D在BC上,
1.如果AD⊥BC,那么∠BAD=∠______,BD=_______
2.如果∠BAD=∠CAD,那么AD⊥_____,BD=______
3.如果BD=CD,那么∠BAD=∠_______,AD⊥______
四、小结
本节课,我们学习了等腰三角形的性质:等腰三角形的两底角相等 (简写“等边对等角”);等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合(简称“三线合一”),它们对今后的学习十分重要,因此要牢记并能熟练应用。用数学语言表述如下:
1.△ABC中,如果AB=AC,那么∠B=∠C。
2.△ABC中,如果A月=AC,D在BC上,那么由条件(1)∠BAD=∠CAD,(2)AD⊥AC,(3)BD=CD中的任意一个都可以推出另外两个。
五、作业
P97练习第1题。
课后反思:
第二课时 等腰三角形(2)
教学目的
1.使学生熟练地运用等腰三角形的性质求等腰三角形内角的角度。
2.通过例题教学,帮助学生总结代数法求几何角度,线段长度的方法。
重点、难点
重点,等腰三角形的性质及其应用。
难点:简洁的逻辑推理。
教学过程
一、复习巩固
1.叙述等腰三角形的性质,它是怎么得到的?
等腰三角形的两个底角相等,也可以简称“等边对等角”。把等腰三角形对折,折叠两部分是互相重合的,即AB与AC重合,点B与点 C重合,线段BD与CD也重合,所以∠B=∠C。
等腰三角形的顶角平分线,底边上的中线和底边上的高线互相重合,简称“三线合一”。由于AD为等腰三角形的对称轴,所以BD= CD,AD为底边上的中线;∠BAD=∠CAD,AD为顶角平分线,∠ADB=∠ADC=90°,AD又为底边上的高,因此“三线合一”。
2.若等腰三角形的两边长为3和4,则其周长为多少?
二、新课
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边都相等。我们把三条边都相等的三角形叫做等边三角形。
等边三角形具有什么性质呢?
1.请同学们画一个等边三角形,用量角器量出各个内角的度数,并提出猜想。
2.你能否用已知的知识,通过推理得到你的猜想是正确的?
等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到∠A=∠B=C,又由∠A+∠B+∠C=180°,从而推出∠A=∠B=∠C=60°。
3.上面的条件和结论如何叙述?
等边三角形的各角都相等,并且每一个角都等于60°。
等边三角形是轴对称图形吗?如果是,有几条对称轴?
等边三角形也称为正三角形。
例1.在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求∠1和∠ADC的度数。
分析:由AB=AC,D为BC的中点,可知AB为 BC底边上的中线,由“三线合一”可知AD是△ABC的顶角平分线,底边上的高,从而∠ADC=90°,∠l=∠BAC,由∠C=∠B=30°,∠BAC可求,所以∠1可求。
问题1:本题若将D是BC边上的中点这一条件改为AD为等腰三角形顶角平分线或底边BC上的高线,其它条件不变,计算的结果是否一样?
问题2:求∠1是否还有其它方法?
三、练习巩固
1.判断下列命题,对的打“√”,错的打“×”。
a.等腰三角形的角平分线,中线和高互相重合()
b.有一个角是60°的等腰三角形,其它两个内角也为60°()
2.如图(2),在△ABC中,已知AB=AC,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。
四、小结
由等腰三角形的性质可以推出等边三角形的各角相等,且都为60°。“三线合一”性质在实际应用中,只要推出其中一个结论成立,其他两个结论一样成立,所以关键是寻找其中一个结论成立的条件。
五、作业
1.P97练习第2、3题。
补充:如图(3),△ABC是等边三角形,BD、CE是中线,求∠CBD,∠BOE,∠BOC,∠EOD的度数。
课后反思:
2.等腰三角形的识别
教学目的
1.通过探索一个三角形是等腰三角形的条件,培养学生的探索能力。
2.能利用一个三角形是等腰三角形的条件,正确判断某个三角形是否为等腰三角形。
重点、难点
重点:让学生掌握一个三角形是等腰三角形的条件和正确应用。
难点:一个三角形是等腰三角形的条件的正确文字叙述。
教学过程
一、复习引入
等腰三角形具有哪些性质?
等腰三角形的两底角相等,底边上的高、中线及顶角平分线“三线合一”。
二、新课
对于一个三角形,怎样识别它是不是等腰三角形呢?我们已经知道的方法是看它是否有两条边相等。这一节,我们再学习另一种识别方法。
我们已学过,等腰三角形的两个底角相等,反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?
为了回答这个问题,请同学们分别拿出一张半透明纸,做一个实验,按以下方法进行操作:
1.在半透明纸上画一个线段BC。
2.以BC为始边,分别以点B和点C为顶点,用量角器画两个相等的角,两角终边的交点为A。
3.用刻度尺找出BC的中点D,连接AD,然后沿AD对折。
问题1:AB与AC是否重合?
问题2:本实验的条件与结论如何用文字语言加以叙述?
如果一个三角形有两个角相等,那么这两个角所对的边也相等,简写成“等角对等边”。
也就是说,如果一个三角形中有两个角相等,那么它就是等腰三角形。一个三角形是等腰三角形的条件,可以用来判定一个三角形是否为等腰三角形。
例1.在△ABC中,已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?
问题3:三个角都是60°的三角形是等边三角形吗?你能说明理由吗?
等腰直角三角形:顶角是直角的等腰三角形是等腰直角三角形,如图所示。
问题4:你能说出等腰直角三角形各角的大小吗?
问题5:请你画一个等腰直角三角形,使∠C=90°,CD是底边上的高,数一数图中共有几个等腰直角三角形?
三、练习巩固
P99练习l、2、3题。
四、小结
这节课,,我们学习了一个三角形是等腰三角形的条件:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”),此条件可以做为判断一个三角形是等腰三角形的依据。因此,要牢记并能熟练应用它。
五、作业
1.P99习题第4、5题。
课后反思:
小结与复习
教学目的
1.使学生对整章的学习内容做一回顾,系统地把握全章的知识要点和基本技能。
2.通过例题和练习,使学生能较好地运用本章知识和技能解决有关问题。
重点、难点
判断图形是否是轴对称图形,线段的垂直平分线、角平分线的性质、等腰三角形的性质和判定及其应用是教学重点,而灵活运用上述性质解决问题、轴对称图案的设计是教学难点。
教学过程
一、知识回顾
问题1:轴对称图形的定义是什么?
它是判断图形是否是轴对称图形的依据。
问题2:是否会画轴对称图形的对称轴?
找出轴对称图形的任一组对称点,连结对称点,画对称点所连线段的垂直平分线,即得到该图形对称轴。
问题3:轴对称图形对称点的连线与对称轴有什么关系?
轴对称图形对称点的连线被对称轴垂直平分。
问题4:线段垂直平分线、角平分线具有什么性质?
线段垂直平分线上的点到线段两端的距离相等;角平分线上的点到角两边的距离相等。
问题5:等腰三角形有什么性质?
等腰三角形底边的中线、高线、顶角的平分线互相重合,等腰三角形的两个底角相等(等边对等角),等边三角形的三个角都等于60°。
问题6:如何判断三角形是等腰三角形?等边三角形?
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);有两个角是60°的三角形是等边三角形,有一个角是60°的等腰三角形是等边三角形。
二、例题
1.下列图案是轴对称图形的有( )
A.1个D.2个C.3个D.4个
2.如右图所示,已知,OC平分∠AOB,D是OC上一点,DE⊥OA,DF⊥OB,垂足为E、F点,那么
(1)∠DEF与∠DFE相等吗?为什么?
(2)OE与OF相等吗?为什么?
三、巩固练习
如右图所示,已知AB=AC,DE垂直平分AB交AC、AB于D、E两点,若AB=12cm,BC=l0cm,∠A=49°14′54″.求△BCD的周长和∠DBC度数。
四、课堂小结
通过本节课复习,同学们应掌握本章知识和技能,并运用所学知识和技能解决问题,
五、作业
课后反思:
第10章 平移与旋转
§10.2 平 移
教学目标:
知识与技能目标:
1.通过具体实例认识图形的平移变换,探索它的基本性质. 2.能按要求作出简单的平面图形平移后的图形.3、要明确平面图形的平移变换,不少平面图案都可以看作是由其中的某一部分,沿着上下或左右的方向,平移若干次而成的。
过程与方法目标:
通过具体实例认识图形的平移变换,通过现实生活中各种丰富的实例,让学生体会图形的平移现象,让学生通过各种图形的平移,体验感受图形平移的主要因素是移动的方向和移动的距离. 探索它的基本性质。
情感与态度目标:
认识和欣赏这些图形的平移变换在现实生活中的应用,体会到数学与实际生活的密切联系,认识到数学的价值。
教学重、难点与关键:
重点:平移的基本内涵与基本性质
难点:发现原图形与平移后图形间的关系。
教学时间安排:3教时
§10.2.1图形的平移
教学程序设计:
一、创设问题情景
1、投影:引言及插图。
2、回忆游乐园内的一些项目,如:旋转木马、荡秋千、小火车、滑梯……
3、观察图片中传送带上的电视机与手扶电梯上的人,回答以下问题:
(1)传送带上每台电视机做什么运动?手扶电梯上的人呢?
(2)传送带上的电视机的形状、大小在运动前后是否发生了改变?手扶电梯上的人呢?
(3)在传送带上,如果电视机的某一按键向前移动了80cm,那么电视机的其他部位向什么方向移动?移动了多少距离?
(4)如果把移动前后的同一台电视机的屏幕分别记为四边形ABCD和四边形EFGH(课件演示),那么四边形ABCD与四边形EFGH的形状、大小是否相同?
4、图案欣赏(课件演示)
二、探究新知
(一)、平移的概念
1.平移的概念:
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移不改变图形的形状和大小。
2.它由什么要素决定?
3.对应点、对应线段、对应角
反馈训练应用提高
P67页练习1、2
(二)、平移的基本性质:
1、想一想:
(1)在上图中,线段AE,BF,CG,DH有怎样的位置关系?
(2)图中每对对应线段之间有怎样的位置关系?
(3)图中有哪些相等的线段、相等的角?
2、归纳平移的基本性质:
经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
3、做一做:
如图所示,△ABE沿射线XY的方向
平移一定距离后成为△CDF.找出图中存在
的平行且相等的三条线段和一组全等三角形.
反馈训练应用提高
1、练习:P68页练习3
2思考:图中的四个小三角形都是等边三角形,
边长为2cm,能通过平移△ABC得到其它
三角形吗?若能,请画出平移的方向,并说出平移的距离.
三、小结提高
1、回顾本节课的活动过程:观察——分析——探索——概括。
2、本节课学到了哪些知识和方法?
四、布置作业
教材第71页习题1、2。
五、反思
§10.2.2 平移的特征
教学程序设计:
一、创设问题情景
上节课你学到了什么?举例
二、探究新知
投影:例1如图11.1.8(1),△ABC经过平移到△A′B′C′的位置,指出平移的方向,并量出平移的距离。
投影:试一试
在如图11.1.9的方格纸中,画出将图中的△ABC向右平移5格后的△A′B′C′,然后再画出将△A′B′C′向上平移2格后的△A″B″C″。△A″B″C″是否可以看成是△ABC经过一次平移而得到的呢?如果是,那么平移的方向和距离分别是什么呢?
投影:做一做
如图11.1.10,在纸上画△ABC和两条平行的对称轴m、n。画出△ABC关于直线m对称的△A′B′C′,再画出△A′B′C′关于直线n对称的△A″B″C″。
观察△ABC和△A″B″C″,你能发现这两个三角形有什么关系吗?
三、反馈训练应用提高
1.平移方格纸中的图形(如图),使点A平移到点A′处,画出平移后的图形。
2.图案欣赏(提高认识)
四、小结提高
1、回顾本节课的活动过程:观察——分析——探索——概括。
2、本节课学到了哪些知识和方法?
五、布置作业
教材第70页练习1、2、3。
六、反思
§10.2图形的平移练习
教学程序设计:
一、创设问题情景
前面你学到了什么?举例
二、探究新知
例:图中的四个小三角形都是等边三角形,边长为2cm,能通过平移△ABC得到其它三角形吗?若能,请画出平移的方向,并说出平移的距离.
随堂练习:(投影)
1、填空:
(1)将线段AB向右平移3cm得到线段CD,如果AB=5 cm,则CD= cm.
(2)将∠ABC向上平移10cm得到∠EFG,如果∠ABC=52°,则∠EFG= °,BF= cm.
(3)将面积为30cm2的等腰直角三角形ABC向下平移20cm,得到△MNP,则△MNP是 三角形,它的面积是 cm2.
2、图中小船经过平移到了新的位置,你发现少了什么?请补上.
3、如图1,在四边形ABCD中,AD∥BC,AB=CD,AD<BC,要探究∠B与∠C的关系,可以采用平移的方法(如图2、3)。请你分别说明图形的形成过程,同时判断∠B与∠C的关系并叙述理由,你还有其他方法吗?请在图1中画出你的方案。
三、小结提高
1、回顾本节课的活动过程:
2、本节课学到了哪些知识和方法?
四、布置作业
教材第71页习题3、4。
五、反思
§10.3 旋 转
教学目标:
知识与技能目标:1.认识图形的旋转变换,掌握它的基本性质. 2.认识旋转对称图形,并能够按要求作出简单的平面图形旋转后的图形.3.培养学生创造图案的设计能力
过程与方法目标:
1.、通过具体实例认识图形的旋转变换,探索它的基本性质.引导学生,探索发现原图形经过旋转后的对应点、对应线段之间的位置关系与数量关系.体验感受图形旋转的主要因素是旋转中心和旋转的角度,从而体会到图形在旋转过程中,图形中的每一点都绕着旋转中转动了相同的角度2.认识旋转对称图形,理解旋转对称图形的概念,重视对学生自行设计旋转对称图形的能力的培养,并能够按要求作出简单的平面图形旋转后的图形.
情感与态度目标:
认识和欣赏这些图形的旋转变换在现实生活中的应用,体会到数学与实际生活的密切联系,经历对生活中与旋转现象有关的图形进行观察、分析、欣赏、交流等活动,发展初步的审美能力,增强对图形欣赏的意识。
教学重、难点:
重点:旋转变换的基本性质,并能根据性质作出简单的平面图形旋转后的图形。
难点:旋转变换的基本性质的探索,作出简单的平面图形旋转后的图形。
§10.3.1 图形的旋转
教学程序设计:
一、创设问题情景
1.课件演示,旋转而动产生的奇妙画面。2.你能自己举出日常生活中的一些事例吗?
二、探究新知1
1.观察图形找出这些图形的共同特征:
2.概念:旋转、旋转中心
三、探究新知2
1.做一做
用一张半透明的薄纸,覆盖在画有任意△AOB的纸上,在薄纸上画出与△AOB重合的一个三角形。然后用一枚图钉在点O处固定,将薄纸绕着图钉(即点O)转动一个角度45,薄纸上的三角形就旋转到了新的位置,标上A′、O′、B′,我们可以认为△AOB旋转45后到了上△A′O′B′。在这样的旋转过程中,你发现了什么?
四、探究新知3
做一做
如图11.2.5,如果旋转中心在△ABC的外面点O处,转动60,将整个△ABC旋转到△A′B′C′的位置。那么这两个三角形的顶点、边与角是如何对应的呢?
五、探究新知4
1、如图11.2.6,△ABC是等边三角形,D是BC上一点,
△ABD经过旋转后到达△ACE的位置。
旋转中心是哪一点?
旋转了多少度?
如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
2、如图11.2.7(1),点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转90呢?
六、小结提高
说说“旋转”的概念,旋转的等量关系。
说说描述“旋转”的过程要注意哪几方面?
七、布置作业
课本P74页练习2、3
八、反思
§10.3.2 旋转的特征
教学程序设计:
一、创设问题情景
回顾旋转的概念
二、探究新知1
探索
观察下面两个图形,你能发现有哪些线段相等?有哪些角相等?
你认为图形旋转的特征是什么?
教师组织学生分组讨论。
练习
1.确定图形中的旋转中心,指出这一图形是由哪个基本图形旋转多少度、旋转几次而生成的(不计颜色)。
2.画出△ABC绕点C逆时针旋转90后的图形
三、小结提高
说说“旋转”的概念,旋转的等量关系。
说说描述“旋转”的过程要注意哪几方面?
四、布置作业
1、画出所给图形绕点O顺时针旋转90后的图形。旋转几次后可以与原图形重合?
2、课本P76页练习1、2、3
五、反思
§10.3.3 旋转对称图形
教学程序设计:
一、创设问题情景
1.回顾旋转的概念
2.如图,画出ΔABC绕O点顺时针旋转60°的图形ΔA’B’C’.
二、探究新知
实验1、画出正方形绕对角线的交点顺时针旋转90°的图形.观察旋转后的图形与原正方形有何关系?
实验2.如图11.2.8所示,电扇的叶片转动120、螺旋桨转动180后,都能与自身重合。
你能再举出一些这样的实例吗?
实验3、用一张半透明的薄纸,覆盖在如11.2.9所示的图形上,在薄纸上画这个图形,使它与如图11.2.9所示的图形重合。然后用一枚图钉在圆心处穿过,将薄纸绕着图钉旋转,观察旋转多少度(小于周角)后,薄纸上的图形能与原图形再一次重合。
问题:前面3个实验有什么共同的特性?
概念:
旋转对称图形:绕着某一点旋转一定角度(小于周角)后能与自身重合的图形.
三、操作训练
操作1:用类似上述的操作方法对如图11.2.10所示的图形进行探索,看看它是不是旋转对称图形?想一想旋转中心在何处?该图形需要旋转多少度后,能与自身重合?该图形是轴对称图形吗?
操作2:图11.2.11所示的图形是轴对称图形,用类似上述的操作方法对图11.2.11所示的图形进行探索,它能通过旋转与自身重合吗?
1.找找看,下面图形中有几匹马?它们的位置关系如何?
2.如图所示的图形绕哪一点旋转多少度后能与自身重合?
3.如图,画出ΔABC绕O点逆时针旋转60°的图形ΔA’B’C’.
四、小结提高
说说“旋转对称”的概念。
说说描述“旋转对称”的过程要注意哪几方面?
想一想:
1、正方形旋转180°后能与自身重合吗?还能旋转几度与自身重合?
2、正五边形、正六边形、正七边形……最小旋转多少度能与自身重合?
五、布置作业
P78页练习1、2、3、4
六、反思
§10.4 中心对称
教学目标:
知识与技能目标:
1、通过具体实例认识中心对称,探索它的基本性质,理解: “连结对称点的线段都经过对称中心,并且被对称中心平分”, “中心对称是旋转角度为180°的特殊的旋转对称” 2、发展学生的合情推理能力,进一步培养学生的数学说理的习惯与能力.
过程与方法目标:
1、让学生自己通过丰富的具体图形认识中心对称与中心对称图形,探索它的基本性质,体会中心对称图形是旋转角度为 180°的特殊的旋转对称图形2、在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,进一步培养学生的数学说理的习惯与能力.
情感与态度目标:
认识和欣赏这些特殊的旋转变换在现实生活中的应用,体会到数学与实际生活的密切联系,经历对生活中与旋转现象有关的图形进行观察、分析、欣赏、交流等活动,发展初步的审美能力,增强对图形欣赏的意识。
教学重、难点与关键:
重点:中心对称的基本性质,并能根据性质作出简单的平面图形中心对称图形。
难点:中心对称的基本性质的探索,作出简单的平面图形中心对称图形。
教时安排:3教时
§10.4中心对称 第一课时
教学程序设计:
一、创设问题情景
课件演示如图11.3.1所示的三个图形都是旋转对称图形。
1、上面图形中哪个图形旋转180°能与自身图形重合?
2、你能自己举出日常生活中旋转180°的一些事例吗?
二、探究新知1
1、一个图形绕着中心点旋转180后能与自身重合,我们就把这种图形叫做中心对称图形, 这个中心点叫做对称中心。
你能举一些中心对称图形吗?他们的对称中心在哪里?
2、把一个图形绕着某一点旋转180,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点
如图11.3.2所示,△ABC与△ADE就是成中心对称的两个三角形,点A是对称中心,
三、探究新知2
在图11.3.3中,△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
归纳板书:
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
反过来,如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成中心对称。
四、探究新知3
例:如图11.3.4(1),已知△ABC和点O,画出△DEF,使△DEF和△ABC关于
点O成中心对称。
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D;
(2)同样画出点B和点C的对称点E和F;
(3)顺次连结DE、EF、FD。
如图11.3.4(2),△DEF即为所求的三角形。
训练应用提高
1、课本P81页练习1、2
2、P82页 读一读
五、小结提高
说说中心对称和中心对称图形的区别和联系。
中心对称有什么基本的性质?
六、布置作业
课本P84页习题1、2
七、反思
§10.4中心对称 第二课时
教学程序设计:
一、创设问题情景
回顾中心对称、中心对称图形及其基本性质
二、探究新知1
1、点A和O,求作A关于O点对称的图形。
2、已知线段AB和点O,求作AB关于点O对称的图形。
3、已知三角形ABC和点O,求作三角形ABC关于点O对称的图形。
4、已知四边形ABCD和点O,求作四边形ABCD关于点O对称的图形。
三、探究新知2
试一试:如图11.3.5所示的两个图形成中心对称,你能找到对称中心吗?
说说你这样画的理由。
反馈训练应用提高
课本P21页1
四、小结提高
说说中心对称和中心对称图形的区别和联系。中心对称有什么基本的性质?
五、布置作业
课本P83页练习1、2
六、反思
§10.4中心对称复习 第三课时
教学程序设计:
一、创设问题情景
回顾中心对称、中心对称图形及其基本性质。
回顾轴对称、轴对称图形及其基本性质。并完成
1、点A和直线l,求作A关于l对称的图形。
2、已知线段AB和点l,求作AB关于点l对称的图形。
3、已知三角形ABC和点l,求作三角形ABC关于点l对称的图形。
二、探究新知1
做一做
如图11.3.6,在纸上画△ABC、点P,以及与△ABC关于点P成中心对称的三角形△A″B″C″。
过点P任意画一条直线,画出△ABC关于此直线对称的△A′B′C′,如图11.3.7。
观察△A′B′C′和△A″B″C″,这两个三角形对称吗?画出使这两个三角形成轴对称的对称轴,你发现了什么?
两次翻折(对称轴互相垂直)与中心对称的关系:
如果对称轴互相垂直,那么两次翻折就相当于一次中心对称,且两条对称轴的垂足为对称中心.
反馈训练应用提高
1、阅读材料:古建筑中的旋转对称
―――从敦煌洞窟到欧洲教堂
2、如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于直线y对称的△A″B″C″,△A″B″C″与△ABC是否关于点O成中心对称?
三、小结提高
两次翻折(对称轴互相垂直)与中心对称的关系。
四、布置作业
课本P84页习题1、2、3、4
五、反思
§10.5 图形的全等
教学目标:
1、通过问题的解决,图形的实例,体验全等图形的形成,体会到如何直观地判别两个图形是全等图形,通过动手实验进一步掌握全等图形的概念,全等多边形的特征;
2、了解全等多边形、对应边、对应顶点、对应角的概念;
3、培养学生动手试验的能力与习惯,树立实践出真知的观念。
重点难点:
1、难点:全等多边形的概念和特征;2、重点:全等多边形的对应元素的确定。
教学过程:
一、复习引入
1、问题1、请同学们观察老师手上的两张照片(1寸和2寸的照片),用你们学过的知识来回答观察到什么?(两张照片是相似图形,其相似比是)
2、请几位同学说说相似图形的特征与识别。
3、问题2:请同学们再观察老师手上的两张照片(都是两寸的照片),也用数学的知识说说观察到什么?(两个图形的形状、大小也一样,即相似屁的相似图形)
本节开始,我们就来探索、研究这种图----§24.1图形的全等
二、新授
1、全等图形
试一试:(课本P85)你能找到几对形状相同、大小一样的图形吗?
(两对:(2)和(4)、(3)和(6))
问:如何判断两个图形的大小和形状是否完全相同的?
(学生各抒已见,给予表扬鼓励)
问:发挥你们的想像,两个大小和形状完全相同的图形叠合在一起,是否完全重合。动手试试。
(可用你们带来的工具) (完全重合)
问:通过动手试验,你得到了什么结论?
(判断两个图形的大小和形状是否完全相同,可以把两个图形叠合在一起,看是否完全重合。)
我们把能够完全重合的两个图形叫做全等形。
练习:(1)课本试一试的图中的 就是全等形。
(2)课本 P87 练习
2、全等多边形及对应顶点、对应边、对应角的概念。
问题3:观察老师的演示(用大小一样的照片,演示翻折、旋转、平移的运动),请问:老师把这些图
形进行哪些运动?形状、大小发生了改变吗?从中你得到了什么结论?
学生发表看法。
老师总结:我们把图形的翻折、旋转、平移称是图形的三种基本的运动,图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的。反过来,两个全等的图形经过这样的运动一定能够重合。
完成课本P85 思考。
由学生的回答中引出:
全等多边形:能够完全重合的两个多边形。
对应顶点:两个全等的多边形,经过运动而重合,相互重合的顶点。
对应边:相互重合的边。
对应角:相互重合的角。
如图24.1.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”)(请同学们试指出两个图形的对应顶点、对应边和对应角。
练习:指出下列各图中的全等三角形,指出对应顶点、对应边、对应角。
由学生的练习中,引导学生讨论:如何记作全等形,能很快地指出对应边、对应角。可以小组讨论交流找出你认为较为科学、合理的方法。
(对应位置的字母,表示两个图形的对应顶点,比如△ABC≌△,A与,B与,C与是对应顶点,对应顶点决定的边是全等三角形的对应边。)
练习:已知;四边形ABCDE≌四边形EFGH,写出它们所有的对应边及对应角。
3、全等多边形的特征、识别。
问题4:依据上面的分析,全等多边形有哪些特征呢?
全等多边形的对应边、对应角分别相等。
如五边形ABCDE≌五边形A′B′C′D′E′
对应角相等:, ,,
对应边相等:,,,
,
实际上这也是我们识别全等多边形的方法,即_______________的两个多边形全等。
例:如图(1)△ABC≌△DEF,你得到 ;
(2) ,可以得到△ABC≌△DEF。
练习:已知如图24.1.4△ABC≌△DEF,△ABC的周长是,,,求△DEF中,边DF的长度。
三、小结
对过本节学习,谈谈你的体会,收获,疑惑。
四、作业
P87习题 1、2
