专题8.11二元一次方程组的应用 基础篇 专项练习(含解析)七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题8.11二元一次方程组的应用 基础篇 专项练习(含解析)七年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 367.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 21:52:21 | ||
图片预览




文档简介
专题8.11 二元一次方程组的应用(基础篇)(专项练习)
一、单选题
1.方程组的解适合方程,则k值为( )
A.2 B. C.1 D.
2.某同学在解关于的二元一次方程时,解得其中“”、“”的地方忘了写上,请你告诉他:“”和“”分别应为( )
A. B.
C. D.
3.为振兴农村经济,某县决定购买A,B两种药材幼苗发给农民栽种,已知购买2棵A种药材幼苗和3棵B种药材幼苗共需41元;购买9棵A种药材幼苗和8棵B种药材幼苗共需137元,若设每棵A种药材幼苗元,每棵B种药材幼苗元,则所列方程组正确的是( )
A. B. C. D.
4.学校计划购买A和B两种品牌的足球,已知一个A品牌足球元,一个B品牌足球元.学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有( )
A.2种 B.3种 C.4种 D.5种
5.甲、乙两个工人按计划一个月应生产680个零件,结果甲超额完成计划的20%,乙超额完成计划的15%,两人一共多生产118个零件,则原计划甲、乙各生产零件数为( )
A.320,360 B.360,320 C.300,380 D.380,380
6.甲是乙现在的年龄时,乙8岁;乙是甲现在年龄时,甲20岁,则( )
A.甲比乙大6岁 B.乙比甲大6岁
C.甲比乙大4岁 D.乙比甲大4岁
7.欣欣服装店某天用相同的价格卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )
A.亏损 B.盈利 C.不盈不亏 D.不确定
8.如图,某农家乐老板计划在一块长130米,宽60米的空地开挖两块形状大小相同的垂钓鱼塘,它们的面积之和为5750平方米,两块垂钓鱼塘之间及周边留有宽度相等的垂钓通道,则垂钓通道的宽度为( )
A. B. C. D.
9.《算法统宗》是一本通俗实用的数学书,也是将数字入诗的代表作,这本书由明代程大位花了近20年完成,程大位还有一首类似二元一次方程组的饮酒数学诗:“肆中饮客乱纷纷,薄酒名脑厚酒醇.醇酒二瓶醉五客,薄酒三瓶醉二人,共同饮了一十六,三十四客醉颜生,试问高明能算士,几多酵酒几多醇?”这首诗是说,好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果34位客人醉倒了,他们总共饮下16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶.依题意,可列方程组为( )
A. B.
C. D.
10.现有57张铁皮盒子,每张铁皮做8个盒身或22个盒底,一个盒身与两个盒底配成一个盒子设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )
A. B.
C. D.
二、填空题
11.在信息加密传输中,发送方将明文加密成密文传输给接收方,接收方收到密文后解密还原为明文,若某种加密规则为:明文m、n对应的密文为,.例如:明文1、2对应的密文是、.当接收方收到密文是6、3,则解密后得到的明文是 .
12.若方程x+y=3,x﹣y=1和x+2my=0有公共解,则m的取值为 .
13.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 分钟.
14.两个两位数的差是18,在较大的两位数的右边接着写上较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.若这两个四位数的和是6666,这两个两位数分别是多少?设较大的两位数为,较小的两位数为,根据题意列出的方程组为 .
15.一旅行团游客入住一家宾馆,如果每一间客房住5人,那么有3人无房可住;如果每一间客房住6人,那么就空出2间客房.设该宾馆有客房x间、房客y人,列出关于x、y的二元一次方程组 .
16.街道为环卫工人发放口罩,如果每人发5个,还剩下3个,如果每人发6个,还缺5个,则一共有 名环卫工人.
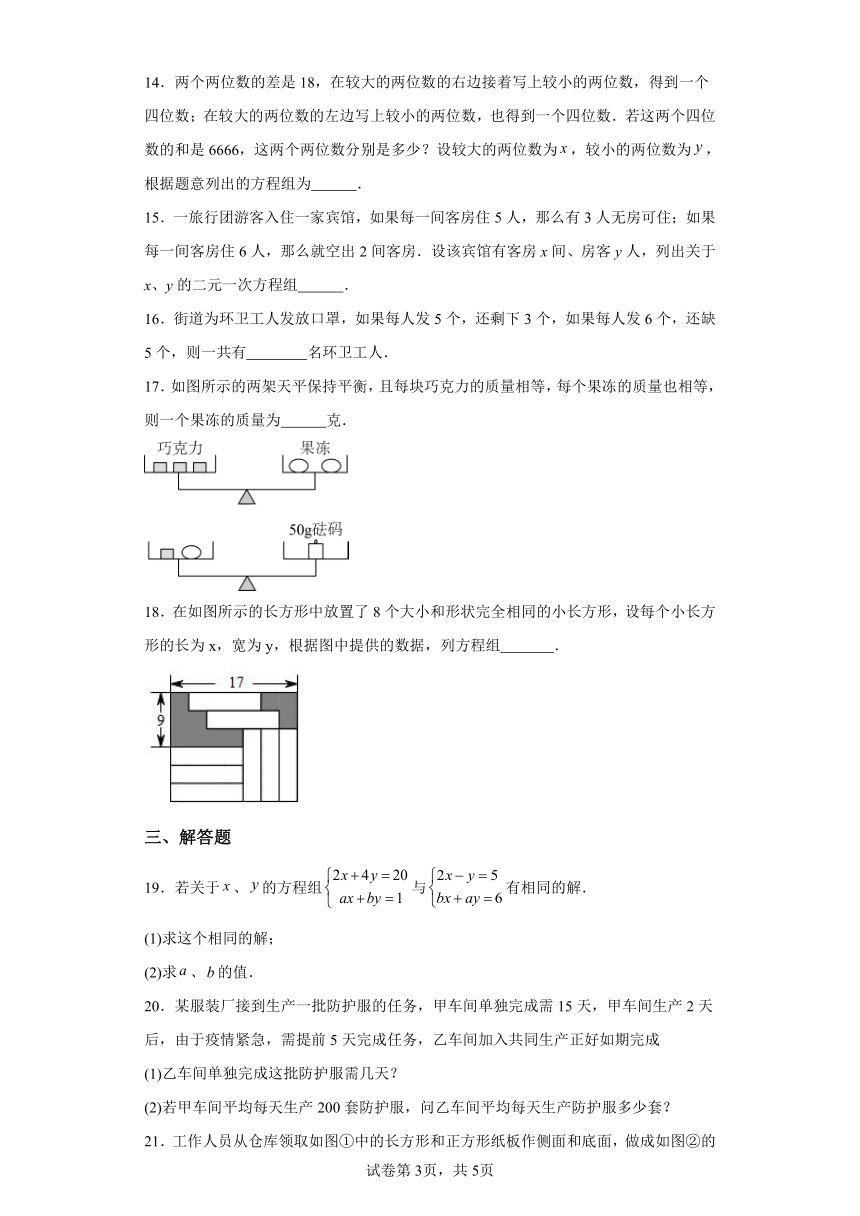
17.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一个果冻的质量为 克.
18.在如图所示的长方形中放置了8个大小和形状完全相同的小长方形,设每个小长方形的长为x,宽为y,根据图中提供的数据,列方程组 .
三、解答题
19.若关于、的方程组与有相同的解.
(1)求这个相同的解;
(2)求、的值.
20.某服装厂接到生产一批防护服的任务,甲车间单独完成需15天,甲车间生产2天后,由于疫情紧急,需提前5天完成任务,乙车间加入共同生产正好如期完成
(1)乙车间单独完成这批防护服需几天?
(2)若甲车间平均每天生产200套防护服,问乙车间平均每天生产防护服多少套?
21.工作人员从仓库领取如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
(1)若工作人员领取正方形纸板560张,长方形纸板940张,请问利用领取的纸板做了竖式与横式纸盒各多少个?
(2)若工作人员某次领取的正方形纸板数与长方形纸板数之比为1:3,请你求出利用这些纸板做出的竖式纸盒与横式纸盒个数的比值.
22.如图,图①是一个长为2n、宽为2m的长方形,沿图中虚线用剪刀平均分成四块小长方形.
(1)图②中拼成的大正方形的面积为 ;
(2)图②中的阴影部分的面积为 ;
(3)若已知图②中拼成的大正方形的周长为28,阴影部分的周长为20,则图①中平均分成的每个小长方形的面积是 .
23.为喜迎元旦,某超市推出A类礼盒和B类礼盒,每个A类礼盒的成本为120元,每个B类礼盒的成本为160元,每个B类礼盒的售价比每个A类礼盒的售价多80元,售卖2个A类礼盒获得的利润和售卖1个B类礼盒获得的利润相同.
(1)求每个A类礼盒的售价;
(2)该超市购进A类礼盒800个和B类礼盒1000个,进行促销活动.超市规定,每人每次最多购买A类礼盒1个或B类礼盒1个,每个A类礼盒直接参与店内“每满100元减a元”的活动,每个B类礼盒在售价的基础上打九折后再参与店内“每满100元减a元”的活动.活动结束时,所有礼盒全部售卖完.若该超市获得的利润为48800元,求a的值.
24.已知关于x.y的方程组,(m,n为实数)
(1)当时,求方程组的解
(2)当时,试探究方程组的解x,y之间的关系.
(3)若方程组的解满足,求分式的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】得,得出,结合条件,即可求解.
【详解】解:
得,
∴,
又,
∴,
解得,
故选A.
【点睛】本题考查了二元一次方程组的解,加减消元法解二元一次方程组,掌握二元一次方程组的解法是解题的关键.
2.A
【分析】把y=1代入第二个方程求出x的值,进而确定出所求即可.
【详解】把y=1代入得:2x 3=5,
解得:x=4,
把x=4,y=1代入得:x+y=5,
则“?”和“ ”分别应为:?=5, =4,
故选:A.
【点睛】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.
3.A
【分析】根据“购买2棵A种药材幼苗和3棵B种药材幼苗共需41元;购买9棵A种药材幼苗和8棵B种药材幼苗共需137元”,即可得出关于,的二元一次方程组,此题得解.
【详解】解:∵购买2棵A种药材幼苗和3棵B种药材幼苗共需41元,
∴;
∵购买9棵A种药材幼苗和8棵B种药材幼苗共需137元,
∴.
∴所列方程组为.
故选:A.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
4.C
【分析】设购买品牌足球个,购买品牌足球个,根据总价单价数量,即可得出关于,的二元一次方程,结合,均为正整数即可求出结论.
【详解】解:设购买品牌足球个,购买品牌足球个,
依题意,得:,
.
,均为正整数,
,,,,
该学校共有种购买方案.
故选C.
【点睛】本题主要考查二元一次方程的解的问题,这类题往往涉及到方案的种类,是常考点.
5.A
【分析】根据题意设原计划甲生产x个零件,乙生产y个零件,根据甲、乙两个工人,按计划本月应共生产680个零件,实际甲超额20%、乙超额15%,因此两人一共多生产118个零件列出方程组,求出方程组的解即可得到结果.
【详解】解:设原计划甲生产x个零件,乙生产y个零件,
根据题意得:,
解得:,即原计划甲生产320个零件,乙生产360个零件.
故选:A.
【点睛】本题考查二元一次方程组的应用,根据题意设未知数并找出题中的等量关系是解答本题的关键.
6.C
【分析】根据题中已知量和未知量之间的等量关系,设未知数,列二元一次方程组即可解决.
【详解】解:设甲现在x岁,乙现在y岁.
根据题意,得,
解得,
∴
故选:C
【点睛】本题考查了列方程组解应用题的知识点,找出题中已知量和未知之间的等量关系是解题的关键.
7.A
【分析】设第一件衣服的进价为x元,第二件衣服的进价为y元,根据题意,可得,进而即可求解.
【详解】设第一件衣服的进价为x元,第二件衣服的进价为y元,
由题意得:
∴,
整理得:
∴
∴该服装店卖出这两件服装的盈利情况是:
,即赔了元.
故选:A.
【点睛】本题主要考查二元一次方程的应用,根据等量关系,列出方程是关键.
8.B
【分析】设垂钓通道的宽度为x米,则两块垂钓鱼塘可合成长为米、宽为米的矩形,根据矩形的面积公式结合绿地的面积为5750平方米,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【详解】解:设垂钓通道的宽度为x米,则两块垂钓鱼塘可合成长为米、宽为米的矩形,
根据题意得: ,
整理得:,
解得:60(舍去),.
即垂钓通道的宽度为5米.
故选:B.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
9.B
【分析】直接利用“好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果34位客人醉倒了,他们总共饮下16瓶酒.”,分别得出等式求出答案.
【详解】解:设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为:
.
故选:B.
【点睛】此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
10.A
【分析】根据①共有57张铁皮;②做的盒底数等于盒身数的2倍时才能正好配套列方程即可.
【详解】解:根据共有57张铁皮,得方程;
根据做的盒底数等于盒身数的2倍时才能正好配套,得方程.
列方程组为.
故选:A.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系是解应用题的关键,寻找第二个相等关系是难点.
11.3,-1
【分析】明文m、n对应的密文为m-3n,2m+3n,当接收方收到密文是6、3时,实际就是转化为二元一次方程组求解问题.
【详解】解:由题意,可得,
解得:,
故答案为:3,-1.
【点睛】本题考查二元一次方程组的应用,关键是理解题意知道传送密码和接收密码的关系列出二元一次方程组求解.
12.-1
【分析】先解方程组得出x、y的值,然后代入x+2my=0,求出m的值即可.
【详解】解:方程x+y=3,x﹣y=1组成方程组,解得:,
∵方程x+y=3,x﹣y=1和x+2my=0有公共解,
∴也是x+2my=0的一个解,
∴,解得:.
故答案为:-1.
【点睛】本题主要考查了方程组的解和解二元一次方程组,正确求出方程组的解,是解题的关键.
13.4
【分析】设同向行驶的相邻两车的距离及车、小王的速度为未知数,等量关系为:6×车速-6×小王的速度=同向行驶的相邻两车的距离;3×车速+3×小王的速度=同向行驶的相邻两车的距离;把相关数值代入可得同向行驶的相邻两车的距离及车的速度关系式,相除可得所求时间.
【详解】解:设18路公交车的速度是x米/分,小王行走的速度是y米/分,同向行驶的相邻两车的间距为s米.
每隔6分钟从背后开过一辆18路公交车,则6x-6y=s.①
每隔3分钟从迎面驶来一辆18路公交车,则3x+3y=s.②
由①,②可得s=4x,
∴.
故答案为:4.
即18路公交车总站发车间隔的时间是4分钟.
【点睛】本题考查二元一次方程组的应用;根据追及问题和相遇问题得到两个等量关系是解决本题的关键;设出所需的多个未知数是解决本题的突破点.
14.
【分析】由较大的两位数为,较小的两位数为,再表示两种情况下的四位数,从而根据相等关系列出方程即可.
【详解】解:∵ 较大的两位数为,较小的两位数为,
∴ 在较大的两位数的右边接着写较小的两位数,得到一个四位数为:,
在较大的两位数的左边接着写较小的两位数,得到一个四位数为:,
又∵两个两位数的差是18,这两个四位数的和是6666,
∴可得:.
故答案为:
【点睛】本题考查的是二元一次方程组的应用,确定相等关系,再根据相等关系列方程是解题的关键.
15.
【分析】设该店有客房x间,房客y人;每一间客房住5人,那么有3人无房可住;如果每一间客房住6人,那么就空出2间客房.再得出方程组即可.
【详解】解:设该店有客房x间,房客y人;根据题意得:
故答案为:.
【点睛】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
16.8
【分析】设一共有x名环卫工人,要发放的口罩共有y个,根据“如果每人发5个,还剩下3个,如果每人发6个,还缺5个”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设一共有x名环卫工人,要发放的口罩共有y个,
依题意,得:,
解得:.
故答案为:8.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
17.
【分析】根据题意可知本题存在两个等量关系式,即三块巧克力的质量等于两个果冻的质量,一个巧克力和一个果冻的质量之和等于克.根据这两个等量关系式列出二元一次方程组即可.
【详解】解:设巧克力的质量为x克,果冻的质量为y克,则
,
解得,
答:一个果冻的质量为克.
故答案为:.
【点睛】本题考查二元一次方程组的应用,根据图中信息正确的列出方程组是解题的关键.
18.
【分析】设小长方形的长为x,宽为y,根据长方形ABCD的长为17,宽的两种不同的表达式列出方程组即可得解;
【详解】解:设小长方形的长为x,宽为y,根据题意得:
,
整理得:;
故答案为:
【点睛】本题考查了二元一次方程组的应用,根据图形,找到合适的等量关系列出方程组是解题的关键.
19.(1)
(2)
【分析】(1)因为两个方程组同解,所以将两个方程组的第一个方程联立,解方程组即可求解.
(2)将(1)所得相同的解代入原方程组,并将含参数a、b的两个方程联立可得方程组,解方程组即可求解.
【详解】(1)因为两个方程组同解,所以将两个方程组的第一个方程联立可得:
解这个方程组可得相同的解为:
(2)将(1)所得相同的解代入原方程组,并将含参数a、b的两个方程联立可得方程组:
解得
【点睛】本题考查了同解方程组,加减消元法解二元一次方程组,二元一次方程组的解的定义,正确的计算是解题的关键.
20.(1)24
(2)125
【分析】(1)根据题意设甲乙每天生产的数量为x、y,可得y=,根据工作效率=工作量÷工作时间,可得乙车间单独完成这批防护服需24天;
(2)根据甲乙车间工作效率关系可求.
【详解】(1)解:设甲每天生产x套,则总任务为15x套,乙每天生产y套,
则(15-5)x+(15-2-5)y=15x,
整理得10x+8y=15x,
∴y=,
∴15x=,
答:乙车间单独完成这批防护服需24天.
(2)解:(套)
答:乙车间平均每天生产防护服125套.
【点睛】本题考查了工程问题,掌握工作总量、工作时间、工作效率之间的关系是解题的关键.
21.(1)做成40个竖式纸盒,260个横式纸盒
(2)竖式纸盒与横式纸盒个数的比值为3
【分析】(1)设做成x个竖式纸盒,y个横式纸盒,则需要正方形纸板(x+2y)张,需要长方形的纸板(4x+3y)张,根据题意列出方程组,解方程组即可求解;
(2)由(1)结合题意可得:,解比例即可求解.
【详解】(1)解:设做成x个竖式纸盒,y个横式纸盒,
则需要正方形纸板(x+2y)张,需要长方形的纸板(4x+3y)张,
由题意可得:,解得:
答:做成40个竖式纸盒,260个横式纸盒;
(2)由题意可得:,
解得:x=3y,
∴x:y=3,
答:竖式纸盒与横式纸盒个数的比值为3.
【点睛】本题考查了二元一次方程组的应用,二元一次方程组的解,理解题意,找到等量关系列出方程组是解题的关键.
22.(1)
(2)
(3)6
【分析】(1)判断出正方形的边长,可得结论;
(2)判断出阴影正方形的的边长,可得结论;
(3)构建方程组,求出m,n可得结论.
【详解】(1)解:∵图②中拼成的大正方形的边长为,
∴面积为;
故答案为:;
(2)解:图②中的阴影部分的边长为,
∴面积为;
故答案为:.
(3)解:∵图②中拼成的大正方形的周长为28,阴影部分的周长为20,
∴图②中拼成的大正方形的边长为7,阴影部分的边长为5,
∴,
解得,
∴每个小长方形的面积.
故答案为:6.
【点睛】本题考查图形的拼剪,正方形的面积公式,以及解二元一次方程组,解题的关键是理解题意,灵活运用所学知识解决问题.
23.(1)每个A类礼盒的售价为160元
(2)14
【分析】(1)设每个A类礼盒的售价为x元,每个B类礼盒的售价为y元,根据“每个B类礼盒的售价比每个A类礼盒的售价多80元,售卖2个A类礼盒获得的利润和售卖1个B类礼盒获得的利润相同”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)由每个B类礼盒售价的九折大于200元,可得出每个B类礼盒的活动价为元,利用总利润等于每个的销售利润乘以销售数量,可得出关于a的一元一次方程,解之即可得出a的值.
【详解】(1)解:设每个A类礼盒的售价为x元,每个B类礼盒的售价为y元,
根据题意得:,
解得:.
答:每个A类礼盒的售价为160元.
(2)解:∵(元),,
∴每个B类礼盒的活动价为元.
根据题意得:,
解得:.
答:a的值为14.
【点睛】本题考查了二元一次方程组的应用以及一元一次方程的应用,解题的关键是:明确题意,准确得到等量关系是解题的关键.
24.(1);(2)x=y;(3)
【分析】(1)把m=-3,n=2代入方程组,解方程组即可;
(2)求出方程组的解,即可得出x,y之间的关系;
(3)把方程组的解代入2x+3y=0,可得8m+2n=0,即4m+n=0,可得n=-4n,再代入所求式子计算即可.
【详解】解:(1)当,时,原方程组为,
解得:;
(2),
①②得:,
代入①得:,
当时,,
则,,
;
(3)由,可得,
即,
,
可得,
把代入分式得
.
【点睛】本题考查了二元一次方程组的解法,考核学生的计算能力,解二元一次方程组的基本思路是消元,把二元方程转化为一元方程是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.方程组的解适合方程,则k值为( )
A.2 B. C.1 D.
2.某同学在解关于的二元一次方程时,解得其中“”、“”的地方忘了写上,请你告诉他:“”和“”分别应为( )
A. B.
C. D.
3.为振兴农村经济,某县决定购买A,B两种药材幼苗发给农民栽种,已知购买2棵A种药材幼苗和3棵B种药材幼苗共需41元;购买9棵A种药材幼苗和8棵B种药材幼苗共需137元,若设每棵A种药材幼苗元,每棵B种药材幼苗元,则所列方程组正确的是( )
A. B. C. D.
4.学校计划购买A和B两种品牌的足球,已知一个A品牌足球元,一个B品牌足球元.学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有( )
A.2种 B.3种 C.4种 D.5种
5.甲、乙两个工人按计划一个月应生产680个零件,结果甲超额完成计划的20%,乙超额完成计划的15%,两人一共多生产118个零件,则原计划甲、乙各生产零件数为( )
A.320,360 B.360,320 C.300,380 D.380,380
6.甲是乙现在的年龄时,乙8岁;乙是甲现在年龄时,甲20岁,则( )
A.甲比乙大6岁 B.乙比甲大6岁
C.甲比乙大4岁 D.乙比甲大4岁
7.欣欣服装店某天用相同的价格卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )
A.亏损 B.盈利 C.不盈不亏 D.不确定
8.如图,某农家乐老板计划在一块长130米,宽60米的空地开挖两块形状大小相同的垂钓鱼塘,它们的面积之和为5750平方米,两块垂钓鱼塘之间及周边留有宽度相等的垂钓通道,则垂钓通道的宽度为( )
A. B. C. D.
9.《算法统宗》是一本通俗实用的数学书,也是将数字入诗的代表作,这本书由明代程大位花了近20年完成,程大位还有一首类似二元一次方程组的饮酒数学诗:“肆中饮客乱纷纷,薄酒名脑厚酒醇.醇酒二瓶醉五客,薄酒三瓶醉二人,共同饮了一十六,三十四客醉颜生,试问高明能算士,几多酵酒几多醇?”这首诗是说,好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果34位客人醉倒了,他们总共饮下16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶.依题意,可列方程组为( )
A. B.
C. D.
10.现有57张铁皮盒子,每张铁皮做8个盒身或22个盒底,一个盒身与两个盒底配成一个盒子设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )
A. B.
C. D.
二、填空题
11.在信息加密传输中,发送方将明文加密成密文传输给接收方,接收方收到密文后解密还原为明文,若某种加密规则为:明文m、n对应的密文为,.例如:明文1、2对应的密文是、.当接收方收到密文是6、3,则解密后得到的明文是 .
12.若方程x+y=3,x﹣y=1和x+2my=0有公共解,则m的取值为 .
13.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 分钟.
14.两个两位数的差是18,在较大的两位数的右边接着写上较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.若这两个四位数的和是6666,这两个两位数分别是多少?设较大的两位数为,较小的两位数为,根据题意列出的方程组为 .
15.一旅行团游客入住一家宾馆,如果每一间客房住5人,那么有3人无房可住;如果每一间客房住6人,那么就空出2间客房.设该宾馆有客房x间、房客y人,列出关于x、y的二元一次方程组 .
16.街道为环卫工人发放口罩,如果每人发5个,还剩下3个,如果每人发6个,还缺5个,则一共有 名环卫工人.
17.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一个果冻的质量为 克.
18.在如图所示的长方形中放置了8个大小和形状完全相同的小长方形,设每个小长方形的长为x,宽为y,根据图中提供的数据,列方程组 .
三、解答题
19.若关于、的方程组与有相同的解.
(1)求这个相同的解;
(2)求、的值.
20.某服装厂接到生产一批防护服的任务,甲车间单独完成需15天,甲车间生产2天后,由于疫情紧急,需提前5天完成任务,乙车间加入共同生产正好如期完成
(1)乙车间单独完成这批防护服需几天?
(2)若甲车间平均每天生产200套防护服,问乙车间平均每天生产防护服多少套?
21.工作人员从仓库领取如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
(1)若工作人员领取正方形纸板560张,长方形纸板940张,请问利用领取的纸板做了竖式与横式纸盒各多少个?
(2)若工作人员某次领取的正方形纸板数与长方形纸板数之比为1:3,请你求出利用这些纸板做出的竖式纸盒与横式纸盒个数的比值.
22.如图,图①是一个长为2n、宽为2m的长方形,沿图中虚线用剪刀平均分成四块小长方形.
(1)图②中拼成的大正方形的面积为 ;
(2)图②中的阴影部分的面积为 ;
(3)若已知图②中拼成的大正方形的周长为28,阴影部分的周长为20,则图①中平均分成的每个小长方形的面积是 .
23.为喜迎元旦,某超市推出A类礼盒和B类礼盒,每个A类礼盒的成本为120元,每个B类礼盒的成本为160元,每个B类礼盒的售价比每个A类礼盒的售价多80元,售卖2个A类礼盒获得的利润和售卖1个B类礼盒获得的利润相同.
(1)求每个A类礼盒的售价;
(2)该超市购进A类礼盒800个和B类礼盒1000个,进行促销活动.超市规定,每人每次最多购买A类礼盒1个或B类礼盒1个,每个A类礼盒直接参与店内“每满100元减a元”的活动,每个B类礼盒在售价的基础上打九折后再参与店内“每满100元减a元”的活动.活动结束时,所有礼盒全部售卖完.若该超市获得的利润为48800元,求a的值.
24.已知关于x.y的方程组,(m,n为实数)
(1)当时,求方程组的解
(2)当时,试探究方程组的解x,y之间的关系.
(3)若方程组的解满足,求分式的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】得,得出,结合条件,即可求解.
【详解】解:
得,
∴,
又,
∴,
解得,
故选A.
【点睛】本题考查了二元一次方程组的解,加减消元法解二元一次方程组,掌握二元一次方程组的解法是解题的关键.
2.A
【分析】把y=1代入第二个方程求出x的值,进而确定出所求即可.
【详解】把y=1代入得:2x 3=5,
解得:x=4,
把x=4,y=1代入得:x+y=5,
则“?”和“ ”分别应为:?=5, =4,
故选:A.
【点睛】此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.
3.A
【分析】根据“购买2棵A种药材幼苗和3棵B种药材幼苗共需41元;购买9棵A种药材幼苗和8棵B种药材幼苗共需137元”,即可得出关于,的二元一次方程组,此题得解.
【详解】解:∵购买2棵A种药材幼苗和3棵B种药材幼苗共需41元,
∴;
∵购买9棵A种药材幼苗和8棵B种药材幼苗共需137元,
∴.
∴所列方程组为.
故选:A.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
4.C
【分析】设购买品牌足球个,购买品牌足球个,根据总价单价数量,即可得出关于,的二元一次方程,结合,均为正整数即可求出结论.
【详解】解:设购买品牌足球个,购买品牌足球个,
依题意,得:,
.
,均为正整数,
,,,,
该学校共有种购买方案.
故选C.
【点睛】本题主要考查二元一次方程的解的问题,这类题往往涉及到方案的种类,是常考点.
5.A
【分析】根据题意设原计划甲生产x个零件,乙生产y个零件,根据甲、乙两个工人,按计划本月应共生产680个零件,实际甲超额20%、乙超额15%,因此两人一共多生产118个零件列出方程组,求出方程组的解即可得到结果.
【详解】解:设原计划甲生产x个零件,乙生产y个零件,
根据题意得:,
解得:,即原计划甲生产320个零件,乙生产360个零件.
故选:A.
【点睛】本题考查二元一次方程组的应用,根据题意设未知数并找出题中的等量关系是解答本题的关键.
6.C
【分析】根据题中已知量和未知量之间的等量关系,设未知数,列二元一次方程组即可解决.
【详解】解:设甲现在x岁,乙现在y岁.
根据题意,得,
解得,
∴
故选:C
【点睛】本题考查了列方程组解应用题的知识点,找出题中已知量和未知之间的等量关系是解题的关键.
7.A
【分析】设第一件衣服的进价为x元,第二件衣服的进价为y元,根据题意,可得,进而即可求解.
【详解】设第一件衣服的进价为x元,第二件衣服的进价为y元,
由题意得:
∴,
整理得:
∴
∴该服装店卖出这两件服装的盈利情况是:
,即赔了元.
故选:A.
【点睛】本题主要考查二元一次方程的应用,根据等量关系,列出方程是关键.
8.B
【分析】设垂钓通道的宽度为x米,则两块垂钓鱼塘可合成长为米、宽为米的矩形,根据矩形的面积公式结合绿地的面积为5750平方米,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
【详解】解:设垂钓通道的宽度为x米,则两块垂钓鱼塘可合成长为米、宽为米的矩形,
根据题意得: ,
整理得:,
解得:60(舍去),.
即垂钓通道的宽度为5米.
故选:B.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
9.B
【分析】直接利用“好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果34位客人醉倒了,他们总共饮下16瓶酒.”,分别得出等式求出答案.
【详解】解:设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为:
.
故选:B.
【点睛】此题主要考查了由实际问题抽象出二元一次方程组,正确得出等量关系是解题关键.
10.A
【分析】根据①共有57张铁皮;②做的盒底数等于盒身数的2倍时才能正好配套列方程即可.
【详解】解:根据共有57张铁皮,得方程;
根据做的盒底数等于盒身数的2倍时才能正好配套,得方程.
列方程组为.
故选:A.
【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系是解应用题的关键,寻找第二个相等关系是难点.
11.3,-1
【分析】明文m、n对应的密文为m-3n,2m+3n,当接收方收到密文是6、3时,实际就是转化为二元一次方程组求解问题.
【详解】解:由题意,可得,
解得:,
故答案为:3,-1.
【点睛】本题考查二元一次方程组的应用,关键是理解题意知道传送密码和接收密码的关系列出二元一次方程组求解.
12.-1
【分析】先解方程组得出x、y的值,然后代入x+2my=0,求出m的值即可.
【详解】解:方程x+y=3,x﹣y=1组成方程组,解得:,
∵方程x+y=3,x﹣y=1和x+2my=0有公共解,
∴也是x+2my=0的一个解,
∴,解得:.
故答案为:-1.
【点睛】本题主要考查了方程组的解和解二元一次方程组,正确求出方程组的解,是解题的关键.
13.4
【分析】设同向行驶的相邻两车的距离及车、小王的速度为未知数,等量关系为:6×车速-6×小王的速度=同向行驶的相邻两车的距离;3×车速+3×小王的速度=同向行驶的相邻两车的距离;把相关数值代入可得同向行驶的相邻两车的距离及车的速度关系式,相除可得所求时间.
【详解】解:设18路公交车的速度是x米/分,小王行走的速度是y米/分,同向行驶的相邻两车的间距为s米.
每隔6分钟从背后开过一辆18路公交车,则6x-6y=s.①
每隔3分钟从迎面驶来一辆18路公交车,则3x+3y=s.②
由①,②可得s=4x,
∴.
故答案为:4.
即18路公交车总站发车间隔的时间是4分钟.
【点睛】本题考查二元一次方程组的应用;根据追及问题和相遇问题得到两个等量关系是解决本题的关键;设出所需的多个未知数是解决本题的突破点.
14.
【分析】由较大的两位数为,较小的两位数为,再表示两种情况下的四位数,从而根据相等关系列出方程即可.
【详解】解:∵ 较大的两位数为,较小的两位数为,
∴ 在较大的两位数的右边接着写较小的两位数,得到一个四位数为:,
在较大的两位数的左边接着写较小的两位数,得到一个四位数为:,
又∵两个两位数的差是18,这两个四位数的和是6666,
∴可得:.
故答案为:
【点睛】本题考查的是二元一次方程组的应用,确定相等关系,再根据相等关系列方程是解题的关键.
15.
【分析】设该店有客房x间,房客y人;每一间客房住5人,那么有3人无房可住;如果每一间客房住6人,那么就空出2间客房.再得出方程组即可.
【详解】解:设该店有客房x间,房客y人;根据题意得:
故答案为:.
【点睛】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
16.8
【分析】设一共有x名环卫工人,要发放的口罩共有y个,根据“如果每人发5个,还剩下3个,如果每人发6个,还缺5个”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【详解】解:设一共有x名环卫工人,要发放的口罩共有y个,
依题意,得:,
解得:.
故答案为:8.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
17.
【分析】根据题意可知本题存在两个等量关系式,即三块巧克力的质量等于两个果冻的质量,一个巧克力和一个果冻的质量之和等于克.根据这两个等量关系式列出二元一次方程组即可.
【详解】解:设巧克力的质量为x克,果冻的质量为y克,则
,
解得,
答:一个果冻的质量为克.
故答案为:.
【点睛】本题考查二元一次方程组的应用,根据图中信息正确的列出方程组是解题的关键.
18.
【分析】设小长方形的长为x,宽为y,根据长方形ABCD的长为17,宽的两种不同的表达式列出方程组即可得解;
【详解】解:设小长方形的长为x,宽为y,根据题意得:
,
整理得:;
故答案为:
【点睛】本题考查了二元一次方程组的应用,根据图形,找到合适的等量关系列出方程组是解题的关键.
19.(1)
(2)
【分析】(1)因为两个方程组同解,所以将两个方程组的第一个方程联立,解方程组即可求解.
(2)将(1)所得相同的解代入原方程组,并将含参数a、b的两个方程联立可得方程组,解方程组即可求解.
【详解】(1)因为两个方程组同解,所以将两个方程组的第一个方程联立可得:
解这个方程组可得相同的解为:
(2)将(1)所得相同的解代入原方程组,并将含参数a、b的两个方程联立可得方程组:
解得
【点睛】本题考查了同解方程组,加减消元法解二元一次方程组,二元一次方程组的解的定义,正确的计算是解题的关键.
20.(1)24
(2)125
【分析】(1)根据题意设甲乙每天生产的数量为x、y,可得y=,根据工作效率=工作量÷工作时间,可得乙车间单独完成这批防护服需24天;
(2)根据甲乙车间工作效率关系可求.
【详解】(1)解:设甲每天生产x套,则总任务为15x套,乙每天生产y套,
则(15-5)x+(15-2-5)y=15x,
整理得10x+8y=15x,
∴y=,
∴15x=,
答:乙车间单独完成这批防护服需24天.
(2)解:(套)
答:乙车间平均每天生产防护服125套.
【点睛】本题考查了工程问题,掌握工作总量、工作时间、工作效率之间的关系是解题的关键.
21.(1)做成40个竖式纸盒,260个横式纸盒
(2)竖式纸盒与横式纸盒个数的比值为3
【分析】(1)设做成x个竖式纸盒,y个横式纸盒,则需要正方形纸板(x+2y)张,需要长方形的纸板(4x+3y)张,根据题意列出方程组,解方程组即可求解;
(2)由(1)结合题意可得:,解比例即可求解.
【详解】(1)解:设做成x个竖式纸盒,y个横式纸盒,
则需要正方形纸板(x+2y)张,需要长方形的纸板(4x+3y)张,
由题意可得:,解得:
答:做成40个竖式纸盒,260个横式纸盒;
(2)由题意可得:,
解得:x=3y,
∴x:y=3,
答:竖式纸盒与横式纸盒个数的比值为3.
【点睛】本题考查了二元一次方程组的应用,二元一次方程组的解,理解题意,找到等量关系列出方程组是解题的关键.
22.(1)
(2)
(3)6
【分析】(1)判断出正方形的边长,可得结论;
(2)判断出阴影正方形的的边长,可得结论;
(3)构建方程组,求出m,n可得结论.
【详解】(1)解:∵图②中拼成的大正方形的边长为,
∴面积为;
故答案为:;
(2)解:图②中的阴影部分的边长为,
∴面积为;
故答案为:.
(3)解:∵图②中拼成的大正方形的周长为28,阴影部分的周长为20,
∴图②中拼成的大正方形的边长为7,阴影部分的边长为5,
∴,
解得,
∴每个小长方形的面积.
故答案为:6.
【点睛】本题考查图形的拼剪,正方形的面积公式,以及解二元一次方程组,解题的关键是理解题意,灵活运用所学知识解决问题.
23.(1)每个A类礼盒的售价为160元
(2)14
【分析】(1)设每个A类礼盒的售价为x元,每个B类礼盒的售价为y元,根据“每个B类礼盒的售价比每个A类礼盒的售价多80元,售卖2个A类礼盒获得的利润和售卖1个B类礼盒获得的利润相同”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)由每个B类礼盒售价的九折大于200元,可得出每个B类礼盒的活动价为元,利用总利润等于每个的销售利润乘以销售数量,可得出关于a的一元一次方程,解之即可得出a的值.
【详解】(1)解:设每个A类礼盒的售价为x元,每个B类礼盒的售价为y元,
根据题意得:,
解得:.
答:每个A类礼盒的售价为160元.
(2)解:∵(元),,
∴每个B类礼盒的活动价为元.
根据题意得:,
解得:.
答:a的值为14.
【点睛】本题考查了二元一次方程组的应用以及一元一次方程的应用,解题的关键是:明确题意,准确得到等量关系是解题的关键.
24.(1);(2)x=y;(3)
【分析】(1)把m=-3,n=2代入方程组,解方程组即可;
(2)求出方程组的解,即可得出x,y之间的关系;
(3)把方程组的解代入2x+3y=0,可得8m+2n=0,即4m+n=0,可得n=-4n,再代入所求式子计算即可.
【详解】解:(1)当,时,原方程组为,
解得:;
(2),
①②得:,
代入①得:,
当时,,
则,,
;
(3)由,可得,
即,
,
可得,
把代入分式得
.
【点睛】本题考查了二元一次方程组的解法,考核学生的计算能力,解二元一次方程组的基本思路是消元,把二元方程转化为一元方程是解题的关键.
答案第1页,共2页
答案第1页,共2页
