人教版七年级上册3.1.1 《一元一次方程》说课稿课件 16张PPT
文档属性
| 名称 | 人教版七年级上册3.1.1 《一元一次方程》说课稿课件 16张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 16:01:47 | ||
图片预览




文档简介
(共16张PPT)
《一元一次方程》说课稿
一教材分析
1.教材分析
2. 学生情况分析
从《课程标准》看,一元一次方程是“数与代数”领域中一块重要的内容,它是所有代数方程的基础。教科书将本节内容安排在第一节,一方面是对前面学段已经学过的有关于算术方法解题和简单方程的运用的进一步发展,另一方面考虑引入一元一次方程后,可以尽早渗透模型化的思想,使学生尽早接触利用一元一次方程解决实际问题的方法。
《课程标准》对一元一次方程这一节的要求是通过具体实例归纳出一元一次方程的概念,列出方程.让学生在归纳和总结的过程中,初步建立数学模型思想,训练学生主动探究的能力,能结合情境发现并提出问题,体会在解决问题中与他人合作的重要性,获得解决问题的经验。
教材建议安排2课时,第一课时引进一元一次方程概念及如何列方程,第二课时主要学习如何求一元一次方程的解.故本节课我确立了“理解一元一次方程概念,找相等关系列方程”为教学的重点.
本课要理解掌握一元一次方程的概念及列方程,学生具有会用算术解题和对方程有初步了解等知识储备,还须具有一定的观察、归纳、探索能力. 目前,我所任教班级的学生数学基础较好,以上所须基本都已具备,但学生的抽象概括、探索能力稍微偏弱一些,探索精神和学习毅力不足.根据我班学生的这些特点,本节课的难点我确立为“分析数量关系,找相等关系,设未知数,列方程”.
二.教学目标
三.课堂结构
能结合具体例子认识一元一次方程的定义,体会设未知数、列方程的过程,会用方程表示简单实际问题的相等关系。
1. 知识技能
2. 数学思考
通过对实际问题的分析,体会从算式到方程是一种进步,归纳并理解一元一次方程的概念,领悟它的意义和作用
用字母表示未知数,找出相等关系,将实际问题抽象为数学问题,通过列方程解决
3. 解决问题
4. 情感态度
激发学生学习数学的热情,鼓励学生进行思考,发展合作交流的意识和能力。
创设情境(5分钟)
探究新知(25分钟)
拓展应用(10分钟)
反思小结(4分钟)
布置作业(1分钟)
五.教学过程
活动1.情境导入 回顾旧知
活动2.联系实际探究新知
活动3.巩固练习拓展思维
活动4.归纳总结巩固发展
四.教学媒体
本课选择在多媒体教室进行讲授,图文并茂、声像俱佳的表现形式极大调动了学生学习本节课的积极性。通过多媒体课件,学生很容易探究出一元一次方程的概念,通过方程解决实际问题。有更多机会动手、动脑、思考与探索,改变了以往的学习方式,提高了课堂效率,充分激发了学生的学习兴趣,体现了学科教学与信息技术整合的优势.取得较好的教学效果.
德国世界杯足球赛场为长方形足球场,周长为310米,长和宽之 差 为25米,足球场长与宽 分 别是多少米?
足球场长与宽 和 为 310÷2=155
足球场的长度为 (155+25)÷2=90米,宽 度为90-25=65米
设球场长度为X米
宽 度用含x的式子表示为(x-25)米.根据“长方形周长=(长 + 宽 )×2”,列方程:
活动1.情境导入回顾旧知
作为引入本课的第一个例子,选用了“世界杯足球赛赛场问题”,以激发学生的学习兴趣,而且设置了符合学生认知水平的问题情境,以达到由浅入深、逐步提高的目的.
从算术到方程是数学进步
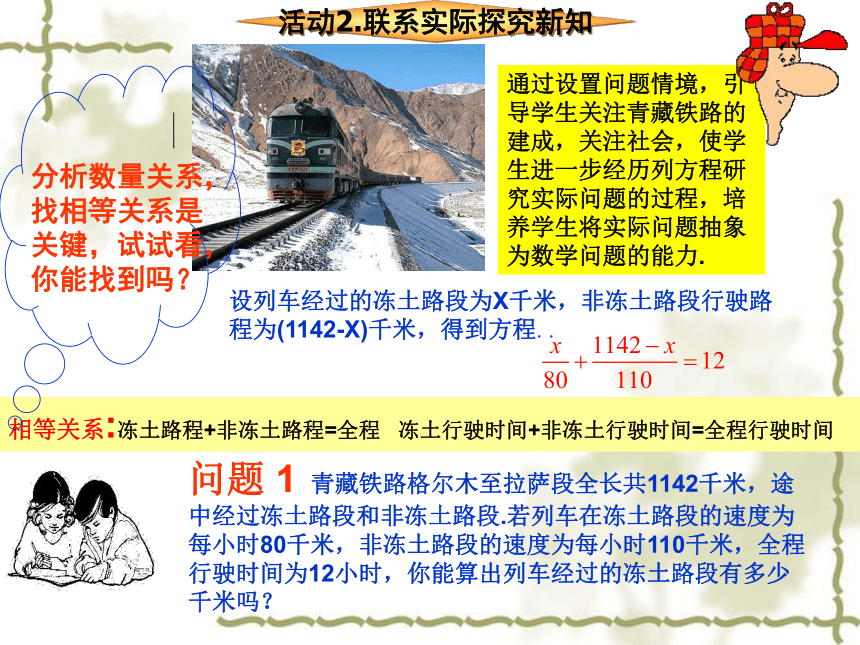
问题 1 青藏铁路格尔木至拉萨段全长共1142千米,途中经过冻土路段和非冻土路段.若列车在冻土路段的速度为每小时80千米,非冻土路段的速度为每小时110千米,全程行驶时间为12小时,你能算出列车经过的冻土路段有多少千米吗?
相等关系:冻土路程+非冻土路程=全程 冻土行驶时间+非冻土行驶时间=全程行驶时间
活动2.联系实际探究新知
设列车经过的冻土路段为X千米,非冻土路段行驶路程为(1142-X)千米,得到方程. .
分析数量关系,找相等关系是关键,试试看,你能找到吗?
通过设置问题情境,引导学生关注青藏铁路的建成,关注社会,使学生进一步经历列方程研究实际问题的过程,培养学生将实际问题抽象为数学问题的能力.
问题 2 学校召开运动会,王平负责给同学们购买饮料.现在要选购两种饮料共40瓶,其中矿泉水1.5元一瓶,茶饮料2元一瓶.王平计划恰好花费65元购买这些饮料,两种饮料应该各买多少瓶呢?
预案1 设购买矿泉水的数量为x瓶,根据第一个相等关系,得到购买茶饮料的数量为(40-x)瓶.根据第二个相等关系得到方程 .
预案2 设购买茶饮料的数量为x瓶,则购买矿泉水的数量为(40-x)瓶,得到方程
预案3 设购买购买矿泉水x瓶,购买茶饮料y瓶,可以列出两个方程 和
相等关系大家能找到吗?
选择与学生生活非常贴近的情境来设计问题,引导学生关注生活及培养学生在生活中应用数学的意识.学生可能设的未知数不同,列出不同的方程,有利于培养学生的发散思维.
相等关系:购买矿泉水数量+购买茶数量=总数量
购买矿泉水费用+购买茶费用=总费用
问题 3 将一个底面半径是5厘米、高为36厘米的“瘦长”型圆柱钢材锻压成高为9厘米的“矮胖”型圆柱钢材,底面半径变成了多少厘米?( )
相等关系是什么呢?
提示一下:圆柱的体积=底面积×高
根据这一相等关系,设底面半径变成了X厘米,列出方程:
设计的问题情境可以让学生关注生产实践,并且前面列出的方程中的未知数指数都是1,而本例列出的方程中的未知数指数是2,可以为归纳一元一次方程的概念提供对比的实例.
只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.
归纳概念
在研究了四个实际问题后,教师引导学生观察得到的方程:
通过观察、思考、分析六个方程的特点,提高学生思考和概括能力,引导学生深层次地参与到概念的形成过程中.
设未知数 列方程
练习:
1.判断下列式子是不是一元一次方程,为什么?
(1)7x+5=9 (2)3x-6 (3) (4)2y+3=-6 (5)x-7y=5 (6)2a>9
活动3.巩固练习拓展思维
通过练习使学生巩固一元一次方程的概念,把握住概念本质.
2. 列方程研究古诗文问题:
隔墙听得客分银,不知人数不知银.七两之多四两,九两分之少半斤.
(注:在古代1斤是16两,半斤就是8两)
设计古诗文应用题的目的是增加数学课的人文色彩,使学生感受数学来源于生活,应用于生活的文化内涵.
你知道什么是九章算术吗?
在我国,“方程”一词最早出现于《九章算术》.《九章算术》全书共分九章,第八章就叫“方程”.
12世纪前后,我国数学家用“天元术”来解题,即先要“立天元为某某”,相当于“设为某某”.
14世纪初,我国元朝数学家朱世杰创立了“四元术”,四元指天、地、人、物,相当于四个未知数.
通过介绍,使学生对方程的知识增加了解,激发学生学习数学,学习方程的热情。
3 设计一道以“2022北京冬奥运会”为实际背景的可列出一元一次方程的应用题,并进行交流.
开放的问题,可以使学生开阔思维,充分发挥想象力和创造力. 小组合作,组间交流,还可以培养学生的合作意识.
小结
本节课学了哪些内容?哪些方法?
方程.一元一次方程的概念
设未知数
找相等关系
用含未知数的式
子表示问题中的数量关系。
列出方程
内容
解决实际问题的方法
列方程
活动4.归纳总结巩固发展
主要由学生进行总结和互相补充,教师只做适当的点拨,以培养学生的归纳概括能力.
作业:
P71
第1、2题
选做题
3.1.1 一元一次方程
1. 一元一次方程的
概念
2.小结
板书设计
为了适应学生不同层次的需求,设计了分层作业.教材上的基础题目可进一步巩固课堂所学知识,选做作业则可以发挥学生学习的自主性.
建构主义强调学生的主体能动性,关注学生对一元一次方程的理解和应用,能否独立探索而得到一元一次方程的概念,能否利用一元一次方程来解决一些实际问题. 在探索概念过程中,关注学生在课堂上的态度、表现,如能否在活动中积极主动的思考,能否积极主动地投入各项活动,是否与伙伴交流自己的想法,听取他人的意见,合作中每个人的责任意识等,在总结过程中关注学生所倾注的情感,对学生及时进行鼓励,促进其学习.
《一元一次方程》说课稿
一教材分析
1.教材分析
2. 学生情况分析
从《课程标准》看,一元一次方程是“数与代数”领域中一块重要的内容,它是所有代数方程的基础。教科书将本节内容安排在第一节,一方面是对前面学段已经学过的有关于算术方法解题和简单方程的运用的进一步发展,另一方面考虑引入一元一次方程后,可以尽早渗透模型化的思想,使学生尽早接触利用一元一次方程解决实际问题的方法。
《课程标准》对一元一次方程这一节的要求是通过具体实例归纳出一元一次方程的概念,列出方程.让学生在归纳和总结的过程中,初步建立数学模型思想,训练学生主动探究的能力,能结合情境发现并提出问题,体会在解决问题中与他人合作的重要性,获得解决问题的经验。
教材建议安排2课时,第一课时引进一元一次方程概念及如何列方程,第二课时主要学习如何求一元一次方程的解.故本节课我确立了“理解一元一次方程概念,找相等关系列方程”为教学的重点.
本课要理解掌握一元一次方程的概念及列方程,学生具有会用算术解题和对方程有初步了解等知识储备,还须具有一定的观察、归纳、探索能力. 目前,我所任教班级的学生数学基础较好,以上所须基本都已具备,但学生的抽象概括、探索能力稍微偏弱一些,探索精神和学习毅力不足.根据我班学生的这些特点,本节课的难点我确立为“分析数量关系,找相等关系,设未知数,列方程”.
二.教学目标
三.课堂结构
能结合具体例子认识一元一次方程的定义,体会设未知数、列方程的过程,会用方程表示简单实际问题的相等关系。
1. 知识技能
2. 数学思考
通过对实际问题的分析,体会从算式到方程是一种进步,归纳并理解一元一次方程的概念,领悟它的意义和作用
用字母表示未知数,找出相等关系,将实际问题抽象为数学问题,通过列方程解决
3. 解决问题
4. 情感态度
激发学生学习数学的热情,鼓励学生进行思考,发展合作交流的意识和能力。
创设情境(5分钟)
探究新知(25分钟)
拓展应用(10分钟)
反思小结(4分钟)
布置作业(1分钟)
五.教学过程
活动1.情境导入 回顾旧知
活动2.联系实际探究新知
活动3.巩固练习拓展思维
活动4.归纳总结巩固发展
四.教学媒体
本课选择在多媒体教室进行讲授,图文并茂、声像俱佳的表现形式极大调动了学生学习本节课的积极性。通过多媒体课件,学生很容易探究出一元一次方程的概念,通过方程解决实际问题。有更多机会动手、动脑、思考与探索,改变了以往的学习方式,提高了课堂效率,充分激发了学生的学习兴趣,体现了学科教学与信息技术整合的优势.取得较好的教学效果.
德国世界杯足球赛场为长方形足球场,周长为310米,长和宽之 差 为25米,足球场长与宽 分 别是多少米?
足球场长与宽 和 为 310÷2=155
足球场的长度为 (155+25)÷2=90米,宽 度为90-25=65米
设球场长度为X米
宽 度用含x的式子表示为(x-25)米.根据“长方形周长=(长 + 宽 )×2”,列方程:
活动1.情境导入回顾旧知
作为引入本课的第一个例子,选用了“世界杯足球赛赛场问题”,以激发学生的学习兴趣,而且设置了符合学生认知水平的问题情境,以达到由浅入深、逐步提高的目的.
从算术到方程是数学进步
问题 1 青藏铁路格尔木至拉萨段全长共1142千米,途中经过冻土路段和非冻土路段.若列车在冻土路段的速度为每小时80千米,非冻土路段的速度为每小时110千米,全程行驶时间为12小时,你能算出列车经过的冻土路段有多少千米吗?
相等关系:冻土路程+非冻土路程=全程 冻土行驶时间+非冻土行驶时间=全程行驶时间
活动2.联系实际探究新知
设列车经过的冻土路段为X千米,非冻土路段行驶路程为(1142-X)千米,得到方程. .
分析数量关系,找相等关系是关键,试试看,你能找到吗?
通过设置问题情境,引导学生关注青藏铁路的建成,关注社会,使学生进一步经历列方程研究实际问题的过程,培养学生将实际问题抽象为数学问题的能力.
问题 2 学校召开运动会,王平负责给同学们购买饮料.现在要选购两种饮料共40瓶,其中矿泉水1.5元一瓶,茶饮料2元一瓶.王平计划恰好花费65元购买这些饮料,两种饮料应该各买多少瓶呢?
预案1 设购买矿泉水的数量为x瓶,根据第一个相等关系,得到购买茶饮料的数量为(40-x)瓶.根据第二个相等关系得到方程 .
预案2 设购买茶饮料的数量为x瓶,则购买矿泉水的数量为(40-x)瓶,得到方程
预案3 设购买购买矿泉水x瓶,购买茶饮料y瓶,可以列出两个方程 和
相等关系大家能找到吗?
选择与学生生活非常贴近的情境来设计问题,引导学生关注生活及培养学生在生活中应用数学的意识.学生可能设的未知数不同,列出不同的方程,有利于培养学生的发散思维.
相等关系:购买矿泉水数量+购买茶数量=总数量
购买矿泉水费用+购买茶费用=总费用
问题 3 将一个底面半径是5厘米、高为36厘米的“瘦长”型圆柱钢材锻压成高为9厘米的“矮胖”型圆柱钢材,底面半径变成了多少厘米?( )
相等关系是什么呢?
提示一下:圆柱的体积=底面积×高
根据这一相等关系,设底面半径变成了X厘米,列出方程:
设计的问题情境可以让学生关注生产实践,并且前面列出的方程中的未知数指数都是1,而本例列出的方程中的未知数指数是2,可以为归纳一元一次方程的概念提供对比的实例.
只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.
归纳概念
在研究了四个实际问题后,教师引导学生观察得到的方程:
通过观察、思考、分析六个方程的特点,提高学生思考和概括能力,引导学生深层次地参与到概念的形成过程中.
设未知数 列方程
练习:
1.判断下列式子是不是一元一次方程,为什么?
(1)7x+5=9 (2)3x-6 (3) (4)2y+3=-6 (5)x-7y=5 (6)2a>9
活动3.巩固练习拓展思维
通过练习使学生巩固一元一次方程的概念,把握住概念本质.
2. 列方程研究古诗文问题:
隔墙听得客分银,不知人数不知银.七两之多四两,九两分之少半斤.
(注:在古代1斤是16两,半斤就是8两)
设计古诗文应用题的目的是增加数学课的人文色彩,使学生感受数学来源于生活,应用于生活的文化内涵.
你知道什么是九章算术吗?
在我国,“方程”一词最早出现于《九章算术》.《九章算术》全书共分九章,第八章就叫“方程”.
12世纪前后,我国数学家用“天元术”来解题,即先要“立天元为某某”,相当于“设为某某”.
14世纪初,我国元朝数学家朱世杰创立了“四元术”,四元指天、地、人、物,相当于四个未知数.
通过介绍,使学生对方程的知识增加了解,激发学生学习数学,学习方程的热情。
3 设计一道以“2022北京冬奥运会”为实际背景的可列出一元一次方程的应用题,并进行交流.
开放的问题,可以使学生开阔思维,充分发挥想象力和创造力. 小组合作,组间交流,还可以培养学生的合作意识.
小结
本节课学了哪些内容?哪些方法?
方程.一元一次方程的概念
设未知数
找相等关系
用含未知数的式
子表示问题中的数量关系。
列出方程
内容
解决实际问题的方法
列方程
活动4.归纳总结巩固发展
主要由学生进行总结和互相补充,教师只做适当的点拨,以培养学生的归纳概括能力.
作业:
P71
第1、2题
选做题
3.1.1 一元一次方程
1. 一元一次方程的
概念
2.小结
板书设计
为了适应学生不同层次的需求,设计了分层作业.教材上的基础题目可进一步巩固课堂所学知识,选做作业则可以发挥学生学习的自主性.
建构主义强调学生的主体能动性,关注学生对一元一次方程的理解和应用,能否独立探索而得到一元一次方程的概念,能否利用一元一次方程来解决一些实际问题. 在探索概念过程中,关注学生在课堂上的态度、表现,如能否在活动中积极主动的思考,能否积极主动地投入各项活动,是否与伙伴交流自己的想法,听取他人的意见,合作中每个人的责任意识等,在总结过程中关注学生所倾注的情感,对学生及时进行鼓励,促进其学习.
