第三章位置与坐标单元复习题 (含解析) 2023—-2024学年北师大版数学八年级上册
文档属性
| 名称 | 第三章位置与坐标单元复习题 (含解析) 2023—-2024学年北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 489.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 17:16:45 | ||
图片预览



文档简介
北师大版八年级数学上册第三章位置与坐标单元复习题
一、选择题
1.某气象台为了预报台风,首先需要确定台风中心的位置,则下列说法能确定台风中心位置的是( )
A.北纬 B.距气象台海里
C.北纬,东经 D.北海市附近
2.某学校的平面示意图如图所示,如果医院所在位置的坐标为,则所在的位置是( )
A.医院 B.学校 C.汽车站 D.水果店
3. 在平面直角坐标系中,下列各点在轴上的是( )
A. B. C. D.
4.若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )
A. B. C. D.
5.在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
6.如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点和点,则第一架轰炸机位于的点P的坐标是( )
A. B. C. D.
7.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1).若点A到x轴的距离与到y轴的距离相等,则a的值为( )
A.1 B.2 C.3 D.1 或 3
8.如果点的坐标满足,那么称点为“美丽点”,若某个“美丽点”到轴的距离为,则点的坐标为( )
A. B.
C.或 D.或
9.在平面直角坐标系中,点关于原点的对称点的坐标是( )
A. B. C. D.
10.如图,在中,点A的坐标为,点C的坐标为,若图中有一点D使与全等,则点D的坐标是( )
A. B. C. D.以上都可以
二、填空题
11. 已知点在轴上,那么点的坐标是 .
12.如图,若“购物中心”用C3表示,则“实验中学”可以表示为 .
13.若点与点关于原点O成中心对称,则m的最小值为 .
14.如图,在平面直角坐标系中,点,,,根据这个规律,探究可得点的坐标是 .
三、解答题
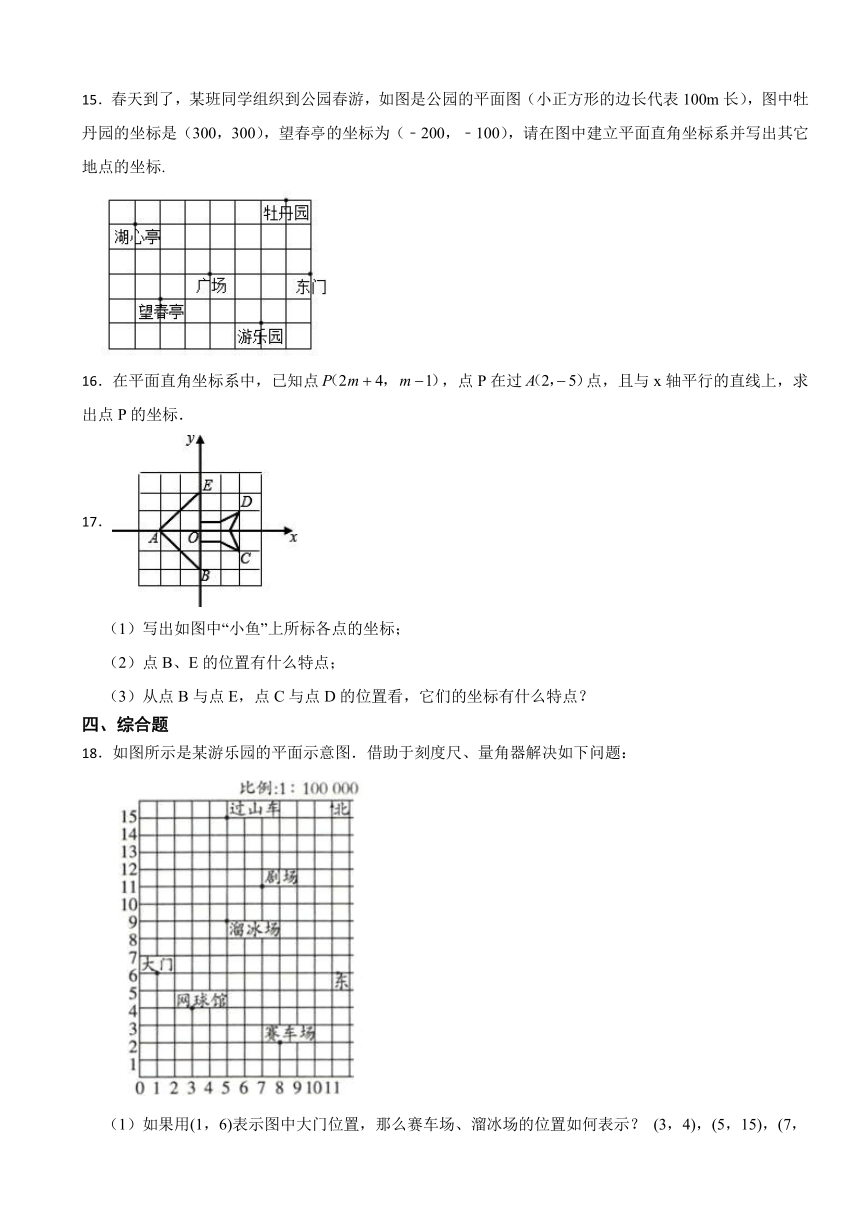
15.春天到了,某班同学组织到公园春游,如图是公园的平面图(小正方形的边长代表100m长),图中牡丹园的坐标是(300,300),望春亭的坐标为(﹣200,﹣100),请在图中建立平面直角坐标系并写出其它地点的坐标.
16.在平面直角坐标系中,已知点,点P在过点,且与x轴平行的直线上,求出点P的坐标.
17.
(1)写出如图中“小鱼”上所标各点的坐标;
(2)点B、E的位置有什么特点;
(3)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
四、综合题
18.如图所示是某游乐园的平面示意图.借助于刻度尺、量角器解决如下问题:
(1)如果用(1,6)表示图中大门位置,那么赛车场、溜冰场的位置如何表示? (3,4),(5,15),(7,11)分别表示哪个地点的位置?
(2)过山车位于大门北偏东多少度方向上?图上距离约为多少厘米?实际距离是多少米?
(3)网球馆在溜冰场什么方向,实际直线距离是多少米?
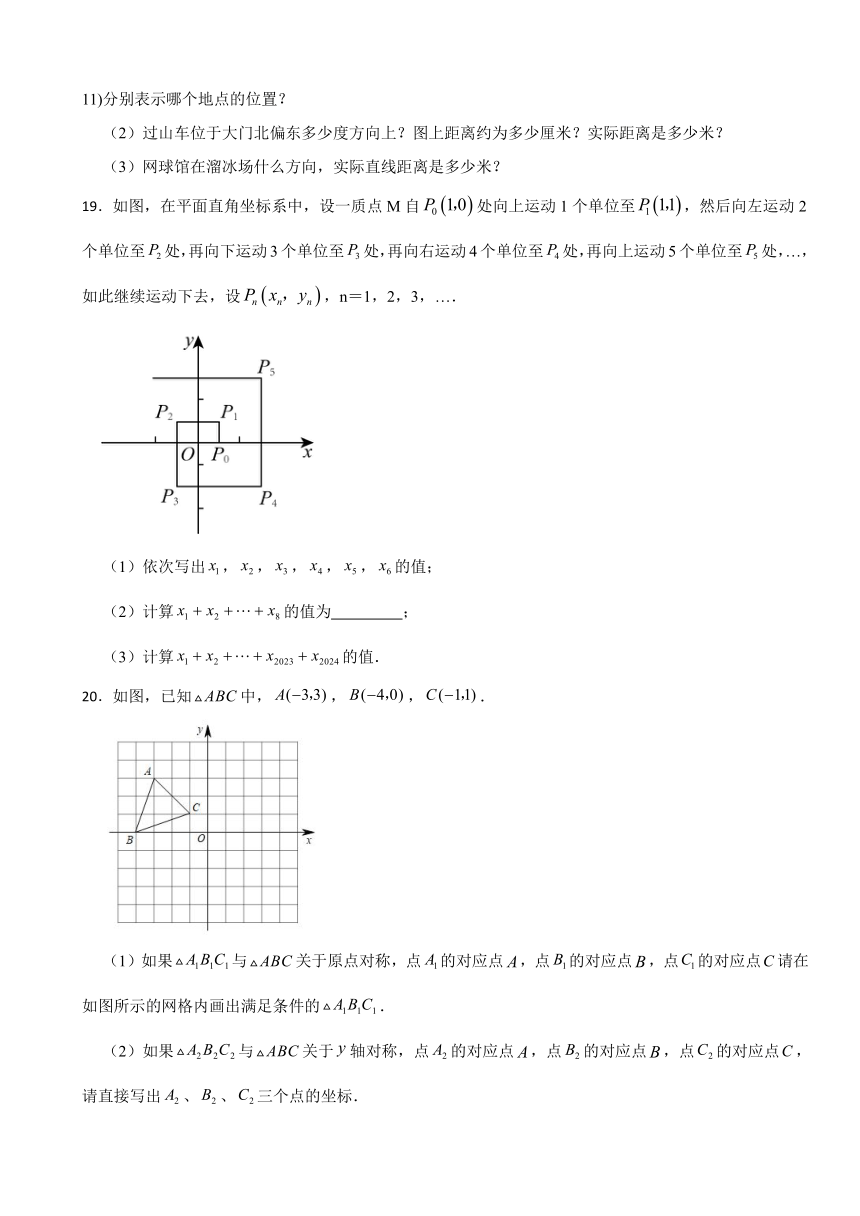
19.如图,在平面直角坐标系中,设一质点M自处向上运动1个单位至,然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,…,如此继续运动下去,设,n=1,2,3,….
(1)依次写出,,,,,的值;
(2)计算的值为 ;
(3)计算的值.
20.如图,已知中,,,.
(1)如果与关于原点对称,点的对应点,点的对应点,点的对应点请在如图所示的网格内画出满足条件的.
(2)如果与关于轴对称,点的对应点,点的对应点,点的对应点,请直接写出、、三个点的坐标.
答案解析部分
1.【答案】C
【解析】【解答】解:A、不能确定台风中心位置,故A不符合题意;
B、不能确定台风中心位置,故B不符合题意;
C、能确定台风中心位置,故C符合题意;
D、不能确定台风中心位置,故D不符合题意.
故答案为:C.
【分析】 根据确定一个物体的位置需要两个量,逐项进行判断,即可得出答案.
2.【答案】C
【解析】【解答】解:如图,
∴(1,2)所在的位置就是汽车站.
故答案为:C.
【分析】根据医院的坐标建立如图所示的平面直角坐标系,进而再确定(1,2)的位置.
3.【答案】B
4.【答案】B
【解析】【解答】解:∵点P到轴的距离是3,到轴的距离是1,
∴点P的横坐标的绝对值为1,纵坐标的绝对值为3,
又∵点在第二象限,
∴点P的坐标为,
故答案为:B.
【分析】根据点的坐标特征可知点P的横坐标的绝对值为1,纵坐标的绝对值为3,然后根据第二象限的点的坐标特征“横坐标为负纵坐标为正”可求解.
5.【答案】D
【解析】【解答】解:由题意可得:
点关于原点对称的点的坐标是
故答案为:D
【分析】根据原点对称的点的坐标特征即可求出答案.
6.【答案】A
【解析】【解答】解:根据最后两架轰炸机分别位于点M(-1,1)和点N(-1,-3)建立直角坐标系,则第一架轰炸机位于的点P的坐标是(3,-1).
故答案为:A.
【分析】根据最后两架轰炸机分别位于点M(-1,1)和点N(-1,-3)建立直角坐标系,结合第一架轰炸机的位置可得相应的坐标.
7.【答案】D
8.【答案】D
【解析】【解答】解:∵P到y轴的距离为2,
∴x=2或-2,
∵x+y=xy,
∴2+y=2y或-2+y=-2y,
∴y=2或y=,
∴P点的坐标为(2,2)或(-2,),
故答案为:D.
【分析】根据一个点到y轴的距离等于其横坐标的绝对值,得出x=2或-2,再根据x+y=xy,得出y=2或y=,即可得出P点的坐标为(2,2)或(-2,).
9.【答案】D
【解析】【解答】解:由题意可得:
点关于原点的对称点的坐标是
故答案为:D
【分析】根据关于原点的对称点的特征即可求出答案。
10.【答案】D
【解析】【解答】解:如图,
解:∵点A的坐标为,点B的坐标为,
∴是平行于x轴的直线.
∵与全等,
∴,
当点D与点C关于直线对称时,
∵点C的坐标是,
∴满足要求.
当点D与点C关于的中垂线对称时,
则满足要求;
当点D与点C关于AB的中点成中心对称时,
则满足要求.
综上可知,点D的坐标是或或.
故答案为:D
【分析】根据轴对称和全等三角形的性质并结合网格图的特征即可求解.
11.【答案】(-4,0)
【解析】【解答】
∵点在轴上,
∴ a+3=0
解得a=-3,
则横坐标a-1=-4
∴ A的坐标是(-4,0)
故答案为:(-4,0).
【分析】本题考查x轴上点的特征。x轴上的点,纵坐标为0,可得a+3=0,得到a值,计算横坐标即可。
12.【答案】A2
【解析】【解答】解:∵“购物中心”用C3表示,
∴“实验中学”可以表示为A2.
故答案为:A2.
【分析】利用坐标表示地理位置的方法求解即可。
13.【答案】-1
【解析】【解答】解:∵点A(1,m)和B(-1,1-|x|) 关于原点O成中心对称,
∴|x|-1=m.
∵|x|≥0,
∴m≥-1,
∴ m的最小值为-1.
故答案为:-1.
【分析】关于原点对称的点,横、纵坐标均互为相反数,则|x|-1=m,然后结合绝对值的非负性可得m的范围,进而可得m的最小值.
14.【答案】
【解析】【解答】解:∵ 点,,, ,
它们的横坐标依次为1,2,3,4,纵坐标依次为2,0,-2,0,2,0,-2,0…
∴2023÷4=505…3,
∴点A2023(2023,-2)
故答案为:(2023,-2).
【分析】 观察图形,利用已知点的坐标可知它们的横坐标依次为1,2,3,4…(序号),纵坐标依次为2,0,-2,0,2,0,-2,0…再用2023÷4,根据其余数可得到点点A2023的坐标.
15.【答案】解:建立平面直角坐标系如图所示;
广场(0,0),湖心亭(﹣300,200),东门(400,0),游乐园(200,﹣200).
【解析】【分析】利用牡丹园的坐标和望春亭的坐标建立平面直角坐标系;根据平面直角坐标系可得到广场,湖心亭,东门,游乐园的坐标.
16.【答案】解:由题意得,,
解得,
∴,
则点P的坐标为.
【解析】【分析】根据题意先求出 , 再求出m=-4,最后求点的坐标即可。
17.【答案】(1)A(-2,0)、B(0,-2)、C(2,-1)、D(2,1)、E(0,2)、O(0,0).
(2)解:点B(0,﹣2)和点E(0,2)关于x轴对称.
(3)解:点B(0,﹣2)与点E(0,2),点C(2,﹣1)与点D(2,1),它们的横坐标相同纵坐标互为相反数.
【解析】【分析】(1)观察直角坐标系,得出各点的坐标。
(2) 观察B、E两点的坐标,可得出两点关于x轴对称。
(3)观察可得,横坐标相同,纵坐标互为相反数。
18.【答案】(1)解:赛车场、溜冰场的位置分别表示为(8,2),(5,9);(3,4),<5,15),(7,11)分别表示网球馆、过山车及剧场
(2)解:北偏东24°方向,图上距离约为3.3 cm,实际距离约为3.3×100 000× =3300(m)
(3)解:南偏西22°方向,图上距离约为1.8 cm,实际直线距离为1 800 m.
【解析】【分析】(1)根据示意图,表示出赛车场和溜冰场的位置,根据坐标确定地点的位置即可。
(2)根据过山车和大门的相对位置,判断方向、距离;
(3)根据网球场和溜冰场的位置,判断方向和距离即可。
19.【答案】(1)解:根据平面直角坐标系结合各点横坐标,得:,,,,,的值分别为1,,,3,3,.
(2)4
(3)解:∵,,…,,…,
,
∴.
【解析】【解答】(2)解:根据平面直角坐标系结合各点横坐标,
∵,
∴,
故答案为:4.
【分析】(1)根据平面直角坐标系结合各点横坐标即可得出答案;
(2)根据4次一循环,找到规律即可求解;
(3)根据(2)的规律即可求解.
20.【答案】(1)解:如图,连接AO,并延长AO到点,使得O=AO,连接BO,并延长BO到点,使得O=BO,连接CO,并延长CO到点,使得O=CO,顺次连接、、,得到,则即为所作;
(2)解:点的坐标是(3,3)点的坐标是(4,0),点的坐标是(1,1)
【解析】【解答】(2)解:∵中,,,,且与关于轴对称,点的对应点,点的对应点,点的对应点,
∴ 点的坐标是(3,3)点的坐标是(4,0),点的坐标是(1,1),
【分析】平面直角坐标系内点的坐标对称原则:(1)关于x轴对称:横坐标不变,纵坐标互为相反数;(2)关于y轴对称:纵坐标不变,横坐标互为相反数;(3)关于原点对称:横、纵坐标都互为相反数。
一、选择题
1.某气象台为了预报台风,首先需要确定台风中心的位置,则下列说法能确定台风中心位置的是( )
A.北纬 B.距气象台海里
C.北纬,东经 D.北海市附近
2.某学校的平面示意图如图所示,如果医院所在位置的坐标为,则所在的位置是( )
A.医院 B.学校 C.汽车站 D.水果店
3. 在平面直角坐标系中,下列各点在轴上的是( )
A. B. C. D.
4.若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )
A. B. C. D.
5.在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
6.如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点和点,则第一架轰炸机位于的点P的坐标是( )
A. B. C. D.
7.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1).若点A到x轴的距离与到y轴的距离相等,则a的值为( )
A.1 B.2 C.3 D.1 或 3
8.如果点的坐标满足,那么称点为“美丽点”,若某个“美丽点”到轴的距离为,则点的坐标为( )
A. B.
C.或 D.或
9.在平面直角坐标系中,点关于原点的对称点的坐标是( )
A. B. C. D.
10.如图,在中,点A的坐标为,点C的坐标为,若图中有一点D使与全等,则点D的坐标是( )
A. B. C. D.以上都可以
二、填空题
11. 已知点在轴上,那么点的坐标是 .
12.如图,若“购物中心”用C3表示,则“实验中学”可以表示为 .
13.若点与点关于原点O成中心对称,则m的最小值为 .
14.如图,在平面直角坐标系中,点,,,根据这个规律,探究可得点的坐标是 .
三、解答题
15.春天到了,某班同学组织到公园春游,如图是公园的平面图(小正方形的边长代表100m长),图中牡丹园的坐标是(300,300),望春亭的坐标为(﹣200,﹣100),请在图中建立平面直角坐标系并写出其它地点的坐标.
16.在平面直角坐标系中,已知点,点P在过点,且与x轴平行的直线上,求出点P的坐标.
17.
(1)写出如图中“小鱼”上所标各点的坐标;
(2)点B、E的位置有什么特点;
(3)从点B与点E,点C与点D的位置看,它们的坐标有什么特点?
四、综合题
18.如图所示是某游乐园的平面示意图.借助于刻度尺、量角器解决如下问题:
(1)如果用(1,6)表示图中大门位置,那么赛车场、溜冰场的位置如何表示? (3,4),(5,15),(7,11)分别表示哪个地点的位置?
(2)过山车位于大门北偏东多少度方向上?图上距离约为多少厘米?实际距离是多少米?
(3)网球馆在溜冰场什么方向,实际直线距离是多少米?
19.如图,在平面直角坐标系中,设一质点M自处向上运动1个单位至,然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,…,如此继续运动下去,设,n=1,2,3,….
(1)依次写出,,,,,的值;
(2)计算的值为 ;
(3)计算的值.
20.如图,已知中,,,.
(1)如果与关于原点对称,点的对应点,点的对应点,点的对应点请在如图所示的网格内画出满足条件的.
(2)如果与关于轴对称,点的对应点,点的对应点,点的对应点,请直接写出、、三个点的坐标.
答案解析部分
1.【答案】C
【解析】【解答】解:A、不能确定台风中心位置,故A不符合题意;
B、不能确定台风中心位置,故B不符合题意;
C、能确定台风中心位置,故C符合题意;
D、不能确定台风中心位置,故D不符合题意.
故答案为:C.
【分析】 根据确定一个物体的位置需要两个量,逐项进行判断,即可得出答案.
2.【答案】C
【解析】【解答】解:如图,
∴(1,2)所在的位置就是汽车站.
故答案为:C.
【分析】根据医院的坐标建立如图所示的平面直角坐标系,进而再确定(1,2)的位置.
3.【答案】B
4.【答案】B
【解析】【解答】解:∵点P到轴的距离是3,到轴的距离是1,
∴点P的横坐标的绝对值为1,纵坐标的绝对值为3,
又∵点在第二象限,
∴点P的坐标为,
故答案为:B.
【分析】根据点的坐标特征可知点P的横坐标的绝对值为1,纵坐标的绝对值为3,然后根据第二象限的点的坐标特征“横坐标为负纵坐标为正”可求解.
5.【答案】D
【解析】【解答】解:由题意可得:
点关于原点对称的点的坐标是
故答案为:D
【分析】根据原点对称的点的坐标特征即可求出答案.
6.【答案】A
【解析】【解答】解:根据最后两架轰炸机分别位于点M(-1,1)和点N(-1,-3)建立直角坐标系,则第一架轰炸机位于的点P的坐标是(3,-1).
故答案为:A.
【分析】根据最后两架轰炸机分别位于点M(-1,1)和点N(-1,-3)建立直角坐标系,结合第一架轰炸机的位置可得相应的坐标.
7.【答案】D
8.【答案】D
【解析】【解答】解:∵P到y轴的距离为2,
∴x=2或-2,
∵x+y=xy,
∴2+y=2y或-2+y=-2y,
∴y=2或y=,
∴P点的坐标为(2,2)或(-2,),
故答案为:D.
【分析】根据一个点到y轴的距离等于其横坐标的绝对值,得出x=2或-2,再根据x+y=xy,得出y=2或y=,即可得出P点的坐标为(2,2)或(-2,).
9.【答案】D
【解析】【解答】解:由题意可得:
点关于原点的对称点的坐标是
故答案为:D
【分析】根据关于原点的对称点的特征即可求出答案。
10.【答案】D
【解析】【解答】解:如图,
解:∵点A的坐标为,点B的坐标为,
∴是平行于x轴的直线.
∵与全等,
∴,
当点D与点C关于直线对称时,
∵点C的坐标是,
∴满足要求.
当点D与点C关于的中垂线对称时,
则满足要求;
当点D与点C关于AB的中点成中心对称时,
则满足要求.
综上可知,点D的坐标是或或.
故答案为:D
【分析】根据轴对称和全等三角形的性质并结合网格图的特征即可求解.
11.【答案】(-4,0)
【解析】【解答】
∵点在轴上,
∴ a+3=0
解得a=-3,
则横坐标a-1=-4
∴ A的坐标是(-4,0)
故答案为:(-4,0).
【分析】本题考查x轴上点的特征。x轴上的点,纵坐标为0,可得a+3=0,得到a值,计算横坐标即可。
12.【答案】A2
【解析】【解答】解:∵“购物中心”用C3表示,
∴“实验中学”可以表示为A2.
故答案为:A2.
【分析】利用坐标表示地理位置的方法求解即可。
13.【答案】-1
【解析】【解答】解:∵点A(1,m)和B(-1,1-|x|) 关于原点O成中心对称,
∴|x|-1=m.
∵|x|≥0,
∴m≥-1,
∴ m的最小值为-1.
故答案为:-1.
【分析】关于原点对称的点,横、纵坐标均互为相反数,则|x|-1=m,然后结合绝对值的非负性可得m的范围,进而可得m的最小值.
14.【答案】
【解析】【解答】解:∵ 点,,, ,
它们的横坐标依次为1,2,3,4,纵坐标依次为2,0,-2,0,2,0,-2,0…
∴2023÷4=505…3,
∴点A2023(2023,-2)
故答案为:(2023,-2).
【分析】 观察图形,利用已知点的坐标可知它们的横坐标依次为1,2,3,4…(序号),纵坐标依次为2,0,-2,0,2,0,-2,0…再用2023÷4,根据其余数可得到点点A2023的坐标.
15.【答案】解:建立平面直角坐标系如图所示;
广场(0,0),湖心亭(﹣300,200),东门(400,0),游乐园(200,﹣200).
【解析】【分析】利用牡丹园的坐标和望春亭的坐标建立平面直角坐标系;根据平面直角坐标系可得到广场,湖心亭,东门,游乐园的坐标.
16.【答案】解:由题意得,,
解得,
∴,
则点P的坐标为.
【解析】【分析】根据题意先求出 , 再求出m=-4,最后求点的坐标即可。
17.【答案】(1)A(-2,0)、B(0,-2)、C(2,-1)、D(2,1)、E(0,2)、O(0,0).
(2)解:点B(0,﹣2)和点E(0,2)关于x轴对称.
(3)解:点B(0,﹣2)与点E(0,2),点C(2,﹣1)与点D(2,1),它们的横坐标相同纵坐标互为相反数.
【解析】【分析】(1)观察直角坐标系,得出各点的坐标。
(2) 观察B、E两点的坐标,可得出两点关于x轴对称。
(3)观察可得,横坐标相同,纵坐标互为相反数。
18.【答案】(1)解:赛车场、溜冰场的位置分别表示为(8,2),(5,9);(3,4),<5,15),(7,11)分别表示网球馆、过山车及剧场
(2)解:北偏东24°方向,图上距离约为3.3 cm,实际距离约为3.3×100 000× =3300(m)
(3)解:南偏西22°方向,图上距离约为1.8 cm,实际直线距离为1 800 m.
【解析】【分析】(1)根据示意图,表示出赛车场和溜冰场的位置,根据坐标确定地点的位置即可。
(2)根据过山车和大门的相对位置,判断方向、距离;
(3)根据网球场和溜冰场的位置,判断方向和距离即可。
19.【答案】(1)解:根据平面直角坐标系结合各点横坐标,得:,,,,,的值分别为1,,,3,3,.
(2)4
(3)解:∵,,…,,…,
,
∴.
【解析】【解答】(2)解:根据平面直角坐标系结合各点横坐标,
∵,
∴,
故答案为:4.
【分析】(1)根据平面直角坐标系结合各点横坐标即可得出答案;
(2)根据4次一循环,找到规律即可求解;
(3)根据(2)的规律即可求解.
20.【答案】(1)解:如图,连接AO,并延长AO到点,使得O=AO,连接BO,并延长BO到点,使得O=BO,连接CO,并延长CO到点,使得O=CO,顺次连接、、,得到,则即为所作;
(2)解:点的坐标是(3,3)点的坐标是(4,0),点的坐标是(1,1)
【解析】【解答】(2)解:∵中,,,,且与关于轴对称,点的对应点,点的对应点,点的对应点,
∴ 点的坐标是(3,3)点的坐标是(4,0),点的坐标是(1,1),
【分析】平面直角坐标系内点的坐标对称原则:(1)关于x轴对称:横坐标不变,纵坐标互为相反数;(2)关于y轴对称:纵坐标不变,横坐标互为相反数;(3)关于原点对称:横、纵坐标都互为相反数。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
