2023-2024学年人教版九年级数学上册 23.2.3关于原点对称的点的坐标教学设计(表格式)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册 23.2.3关于原点对称的点的坐标教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 58.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 19:06:10 | ||
图片预览

文档简介
课题:23.2.3 关于原点对称的点的坐标教学设计
教学目标 1.引导运用中心对称的性质,经历关于原点对称的两点的坐标特征探索过程,能写出关于原点对称的点的坐标。 2.感悟关于原点对称的点的坐标特征,能在平面直角坐标系中作图,体验数形结合的思想。 3.通过探索关于原点对称的点的坐标特征,经历化归思想,会用数形结合的方法分析和解决问题。
教学重难点 教学重点:掌握关于原点对称的两点的坐标特征 教学难点:利用原点对称的两点的坐标特征,在平面直角坐标系中作图。
教学准备 课件,带网格的平面直角坐标系用纸。
教学环节 教学内容 学生活动 设计意图
一 复习引入 二探究新知 三 运用新知 四 课堂小结 教师提问:1、什么叫中心对称? 2、中心对称有什么性质? 3、如图,以O为对称中心,画出点A关于点O的对称点A′. (
O
) (
A
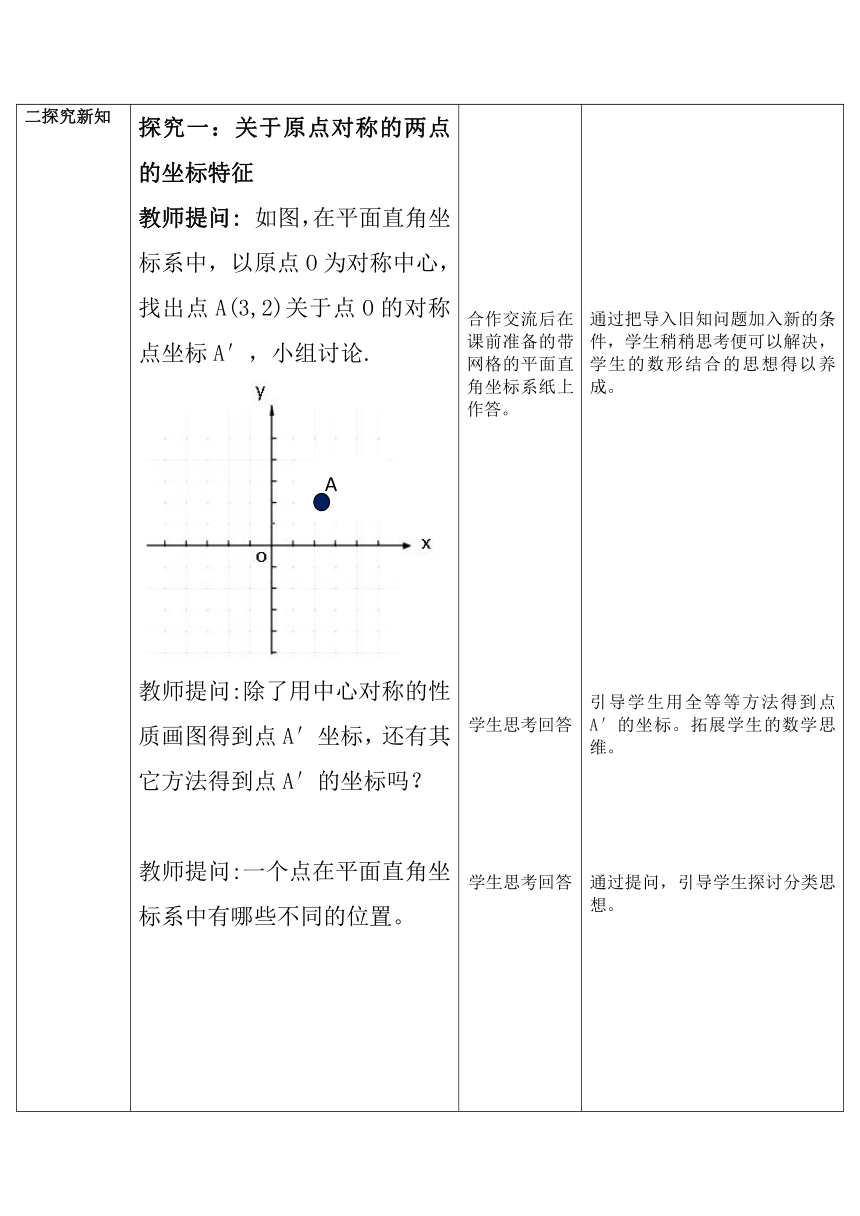
) 探究一:关于原点对称的两点的坐标特征 教师提问: 如图,在平面直角坐标系中,以原点O为对称中心,找出点A(3,2)关于点O的对称点坐标A′,小组讨论. (
A
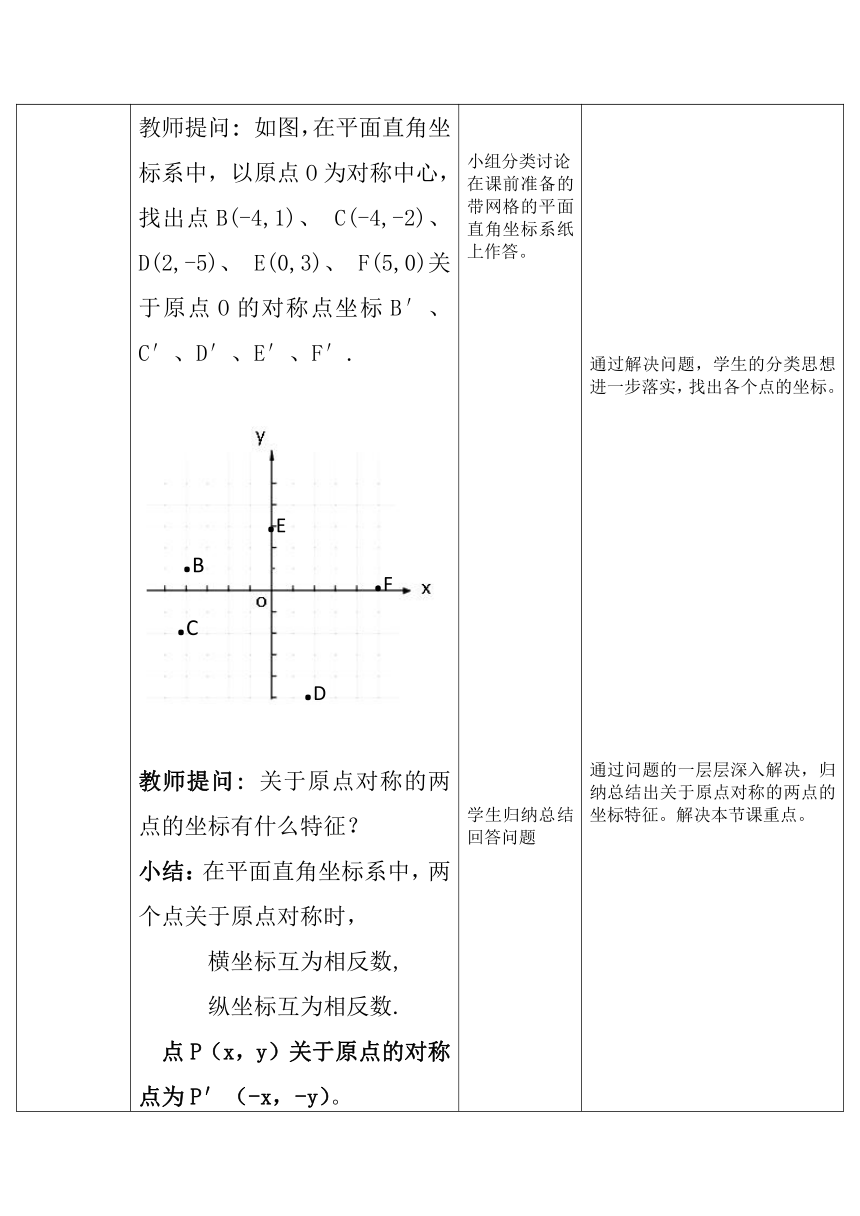
) 教师提问:除了用中心对称的性质画图得到点A′坐标,还有其它方法得到点A′的坐标吗? 教师提问:一个点在平面直角坐标系中有哪些不同的位置。 教师提问: 如图,在平面直角坐标系中,以原点O为对称中心,找出点B(-4,1)、 C(-4,-2)、 D(2,-5)、 E(0,3)、 F(5,0)关于原点O的对称点坐标B′、C′、D′、E′、F′. (
.
F
) (
.
E
) (
.
D
) (
.
C
) (
.
B
B
) 教师提问: 关于原点对称的两点的坐标有什么特征? 小结:在平面直角坐标系中,两个点关于原点对称时, 横坐标互为相反数, 纵坐标互为相反数. 点P(x,y)关于原点的对称点为P′(-x,-y)。 教师提问:1.已知点P坐标为( 6,-3),点P关于x轴对称的点的坐标_________. 2. 已知点Q坐标为( 5,4),点Q关于y轴对称的点的坐标_________. 教师提问:在平面直角坐标系中,关于x轴对称的两点坐标有什么关系,关于y轴对称的两点坐标有什么关系。 小结:在平面直角坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数 点M(x,y)关于x轴的对称点为M′(x,-y) 在平面直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数 点N(x,y)关于y轴的对称点为N′(-x,y) 探究二:利用关于原点对称的点的坐标的关系,作出关于原点对称的图形. 利用关于原点对称的点的坐标的关系,作出与△ABC关于原点对称的图形. 解:点P(x,y)关于原点的对称点为P′(-x,-y),因此△ABC的三个顶点A(-4,1),B(-1,-1),C(-3,2)关于原点的对称点分别为A′(4,-1),B′(1,1),C′(3,-2),依次连接A′B′,B′C′,C′A′,就可以得到与△ABC关于原点对称的△A′B′C′. 1.点A(2,-1)关于原点O对称点的坐标是_______. 2.写出下列各点关于原点的对称点A′,B′,C′,D′的坐标: A(3,1)、B(-2,3)、C(-1,-2)、D(2,-3) 3. 点 A(a,1)与点 A′(5,b)关于原点对称,求a+b的值。 4.如图,已知点A的坐标为( , 2),点B 的坐标为(-1,),在平面直角坐标系中画出点A,点B关于原点的对称点点C,点D, 并写出 C、D 两点的坐标.连接点A,点B,点C,点D,判断四边形ABCD的形状. (
B
) (
A
) 同学们,通过这节课的学习,你有什么收获? 回答问题 在课前准备的带网格的平面直角坐标系纸上作答。 合作交流后在课前准备的带网格的平面直角坐标系纸上作答。 学生思考回答 学生思考回答 小组分类讨论 在课前准备的带网格的平面直角坐标系纸上作答。 学生归纳总结回答问题 学生回答问题 学生归纳总结回答问题 在课前准备的带网格的平面直角坐标系纸上作答。 回答问题 学生归纳总结 回顾旧知,以便探索新知 复习旧知解决问题让学生容易进入学习状态,激发学生学习兴趣。 通过把导入旧知问题加入新的条件,学生稍稍思考便可以解决,学生的数形结合的思想得以养成。 引导学生用全等等方法得到点A′的坐标。拓展学生的数学思维。 通过提问,引导学生探讨分类思想。 通过解决问题,学生的分类思想进一步落实,找出各个点的坐标。 通过问题的一层层深入解决,归纳总结出关于原点对称的两点的坐标特征。解决本节课重点。 1、2题通过与旧知对比联想,深入记忆新知,运用化归的思想。 利用原点对称的两点的坐标特征,在平面直角坐标系中作图,会用数形结合的方法分析和解决问题。 1、2题考查学生直接应用新知的能力 3、4题在掌握新知的基础上,体验数形结合思想,灵活运用新知分析,解决问题。 通过总结感受数学的美,体会化归思想的养成。
板书设计: 关于原点对称的点的坐标 在平面直角坐标系中,关于原点对称点的,横坐标互为相反数,纵坐标互为相反数. 点P(x,y)关于原点的对称点为P′(-x,-y)
教学反思:
教学目标 1.引导运用中心对称的性质,经历关于原点对称的两点的坐标特征探索过程,能写出关于原点对称的点的坐标。 2.感悟关于原点对称的点的坐标特征,能在平面直角坐标系中作图,体验数形结合的思想。 3.通过探索关于原点对称的点的坐标特征,经历化归思想,会用数形结合的方法分析和解决问题。
教学重难点 教学重点:掌握关于原点对称的两点的坐标特征 教学难点:利用原点对称的两点的坐标特征,在平面直角坐标系中作图。
教学准备 课件,带网格的平面直角坐标系用纸。
教学环节 教学内容 学生活动 设计意图
一 复习引入 二探究新知 三 运用新知 四 课堂小结 教师提问:1、什么叫中心对称? 2、中心对称有什么性质? 3、如图,以O为对称中心,画出点A关于点O的对称点A′. (
O
) (
A
) 探究一:关于原点对称的两点的坐标特征 教师提问: 如图,在平面直角坐标系中,以原点O为对称中心,找出点A(3,2)关于点O的对称点坐标A′,小组讨论. (
A
) 教师提问:除了用中心对称的性质画图得到点A′坐标,还有其它方法得到点A′的坐标吗? 教师提问:一个点在平面直角坐标系中有哪些不同的位置。 教师提问: 如图,在平面直角坐标系中,以原点O为对称中心,找出点B(-4,1)、 C(-4,-2)、 D(2,-5)、 E(0,3)、 F(5,0)关于原点O的对称点坐标B′、C′、D′、E′、F′. (
.
F
) (
.
E
) (
.
D
) (
.
C
) (
.
B
B
) 教师提问: 关于原点对称的两点的坐标有什么特征? 小结:在平面直角坐标系中,两个点关于原点对称时, 横坐标互为相反数, 纵坐标互为相反数. 点P(x,y)关于原点的对称点为P′(-x,-y)。 教师提问:1.已知点P坐标为( 6,-3),点P关于x轴对称的点的坐标_________. 2. 已知点Q坐标为( 5,4),点Q关于y轴对称的点的坐标_________. 教师提问:在平面直角坐标系中,关于x轴对称的两点坐标有什么关系,关于y轴对称的两点坐标有什么关系。 小结:在平面直角坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数 点M(x,y)关于x轴的对称点为M′(x,-y) 在平面直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数 点N(x,y)关于y轴的对称点为N′(-x,y) 探究二:利用关于原点对称的点的坐标的关系,作出关于原点对称的图形. 利用关于原点对称的点的坐标的关系,作出与△ABC关于原点对称的图形. 解:点P(x,y)关于原点的对称点为P′(-x,-y),因此△ABC的三个顶点A(-4,1),B(-1,-1),C(-3,2)关于原点的对称点分别为A′(4,-1),B′(1,1),C′(3,-2),依次连接A′B′,B′C′,C′A′,就可以得到与△ABC关于原点对称的△A′B′C′. 1.点A(2,-1)关于原点O对称点的坐标是_______. 2.写出下列各点关于原点的对称点A′,B′,C′,D′的坐标: A(3,1)、B(-2,3)、C(-1,-2)、D(2,-3) 3. 点 A(a,1)与点 A′(5,b)关于原点对称,求a+b的值。 4.如图,已知点A的坐标为( , 2),点B 的坐标为(-1,),在平面直角坐标系中画出点A,点B关于原点的对称点点C,点D, 并写出 C、D 两点的坐标.连接点A,点B,点C,点D,判断四边形ABCD的形状. (
B
) (
A
) 同学们,通过这节课的学习,你有什么收获? 回答问题 在课前准备的带网格的平面直角坐标系纸上作答。 合作交流后在课前准备的带网格的平面直角坐标系纸上作答。 学生思考回答 学生思考回答 小组分类讨论 在课前准备的带网格的平面直角坐标系纸上作答。 学生归纳总结回答问题 学生回答问题 学生归纳总结回答问题 在课前准备的带网格的平面直角坐标系纸上作答。 回答问题 学生归纳总结 回顾旧知,以便探索新知 复习旧知解决问题让学生容易进入学习状态,激发学生学习兴趣。 通过把导入旧知问题加入新的条件,学生稍稍思考便可以解决,学生的数形结合的思想得以养成。 引导学生用全等等方法得到点A′的坐标。拓展学生的数学思维。 通过提问,引导学生探讨分类思想。 通过解决问题,学生的分类思想进一步落实,找出各个点的坐标。 通过问题的一层层深入解决,归纳总结出关于原点对称的两点的坐标特征。解决本节课重点。 1、2题通过与旧知对比联想,深入记忆新知,运用化归的思想。 利用原点对称的两点的坐标特征,在平面直角坐标系中作图,会用数形结合的方法分析和解决问题。 1、2题考查学生直接应用新知的能力 3、4题在掌握新知的基础上,体验数形结合思想,灵活运用新知分析,解决问题。 通过总结感受数学的美,体会化归思想的养成。
板书设计: 关于原点对称的点的坐标 在平面直角坐标系中,关于原点对称点的,横坐标互为相反数,纵坐标互为相反数. 点P(x,y)关于原点的对称点为P′(-x,-y)
教学反思:
同课章节目录
