第五单元_第07课时 有关“外方内圆”和“外圆内方”的实际问题教学课件(共19张PPT)六年级数学上册人教版
文档属性
| 名称 | 第五单元_第07课时 有关“外方内圆”和“外圆内方”的实际问题教学课件(共19张PPT)六年级数学上册人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 09:50:10 | ||
图片预览




文档简介
(共19张PPT)
第7课时 有关“外方内圆”和“外圆内方”的实际问题
小学数学·六年级(上)·RJ
情境导入
中国古代建筑具有悠久的历史传统和光辉的成就。
这些建筑中藏着很多的古人的智慧,我们一起来看看!
结合具体情境,认识组合图形的特征。
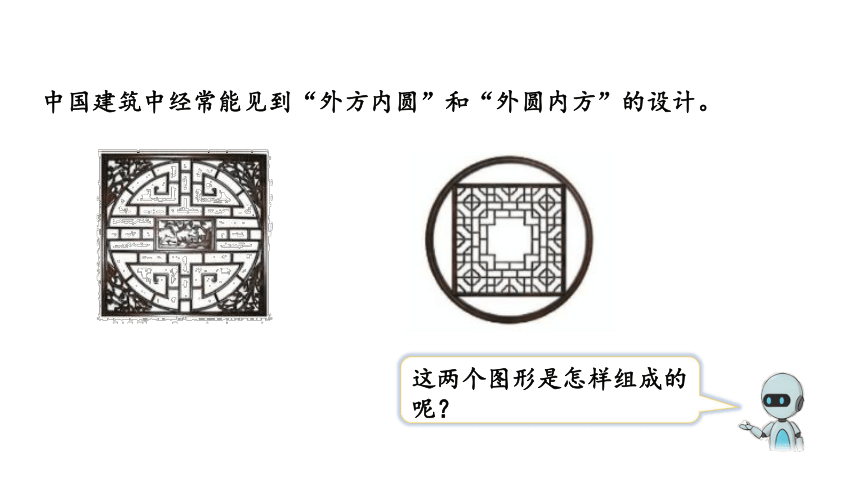
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
这两个图形是怎样组成的呢?
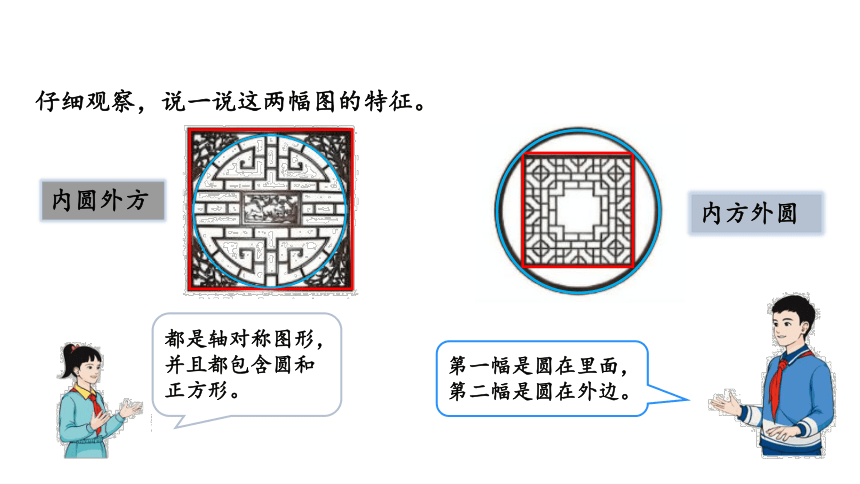
仔细观察,说一说这两幅图的特征。
都是轴对称图形,并且都包含圆和正方形。
第一幅是圆在里面,第二幅是圆在外边。
内圆外方
内方外圆
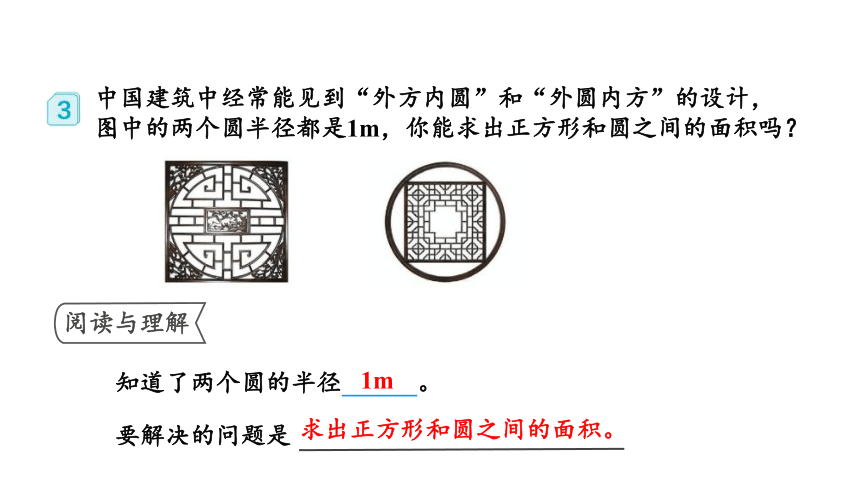
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计,图中的两个圆半径都是1m,你能求出正方形和圆之间的面积吗?
阅读与理解
知道了两个圆的半径______。
1m
求出正方形和圆之间的面积。
要解决的问题是
分析与理解
左图求的是正方形比圆多的面积,
右图求的是圆比正方形多的面积。
两个圆的半径都是1 m。怎样求求正方形和圆之间部分的面积呢?
掌握“内圆外方”和“外圆内方”的图形面积的计算方法。
“外方内圆”
“外方内圆”中正方形的边长与圆的直径长度相等。
阴影部分的面积=正方形的面积-圆的面积
正方形的面积:2×2=4(m )
正方形比圆多的面积:4-3.14=0.86(m )
圆的面积:3.14×1 =3.14(m )
“外圆内方”
“外圆内方”中正方形的边长是多少呢?
可以把图中的正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
圆比正方形多的面积:3.14 - 2=1.14(m )
圆的面积:3.14×1 =3.14(m )
阴影部分的面积=圆的面积-正方形的面积
×(2×1)
×2
=2(m )
正方形的面积:
“外圆内方”
左图:(2r ) -π×r =(4-π)r
右图:π×r -( ×2r ×r )×2=(π -2)r
回顾与反思
如果两个圆的半径都是r,结果又是怎样的?
掌握组合图形的特征,能灵活的计算其中的部分的面积。
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。外面的圆与内部的正方形之间的面积是多少?
圆的面积:3.14×(24÷2) =452.16(cm )
正方形的面积: ×24 × 12 × 2=288(cm )
圆比正方形多的面积:452.16-288=164.16(cm )
答:外面的圆与内部的正方形之间的面积是164.16 cm 。
2.王师傅做一个零件,零件的形状是圆内接正方形,已知圆的直径为12 cm,你能计算出正方形的面积吗?
答:正方形的面积是72cm 。
圆的半径:12÷2=6(cm)
正方形的面积:
×6 × 12 × 2=72(cm )
1
2
3.求下面涂色部分的面积。
圆面积:
3.14×(40÷2)2
=3.14×400
=1256(平方厘米)
正方形面积:
40×40=1600(平方厘米)
涂色部分面积:
1600-1256=344(平方厘米)
4.求图中阴影的面积。
空白部分面积:10 -10 ×3.14×0.25
阴影部分的面积:10 -43=57(平方厘米)
=100-78.5
21.5×2=43(平方厘米)
=21.5(平方厘米)
阴影部分的面积=正方形的面积-空白部分的面积。
生活数学
5.有一栋底面呈长方形的建筑物(如下图),墙角有一根木桩,木桩上拴着一条狗。拴狗的绳子长4 m,这条狗活动区域的面积有多大
1.在正方形内画一个最大的圆,正方形和圆
之间部分的面积为:
2.在圆内画一个最大的正方形,正方形和圆
之间部分的面积为:
S正-S圆
S圆-S正
第7课时 有关“外方内圆”和“外圆内方”的实际问题
小学数学·六年级(上)·RJ
情境导入
中国古代建筑具有悠久的历史传统和光辉的成就。
这些建筑中藏着很多的古人的智慧,我们一起来看看!
结合具体情境,认识组合图形的特征。
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
这两个图形是怎样组成的呢?
仔细观察,说一说这两幅图的特征。
都是轴对称图形,并且都包含圆和正方形。
第一幅是圆在里面,第二幅是圆在外边。
内圆外方
内方外圆
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计,图中的两个圆半径都是1m,你能求出正方形和圆之间的面积吗?
阅读与理解
知道了两个圆的半径______。
1m
求出正方形和圆之间的面积。
要解决的问题是
分析与理解
左图求的是正方形比圆多的面积,
右图求的是圆比正方形多的面积。
两个圆的半径都是1 m。怎样求求正方形和圆之间部分的面积呢?
掌握“内圆外方”和“外圆内方”的图形面积的计算方法。
“外方内圆”
“外方内圆”中正方形的边长与圆的直径长度相等。
阴影部分的面积=正方形的面积-圆的面积
正方形的面积:2×2=4(m )
正方形比圆多的面积:4-3.14=0.86(m )
圆的面积:3.14×1 =3.14(m )
“外圆内方”
“外圆内方”中正方形的边长是多少呢?
可以把图中的正方形看成两个三角形,它的底是圆的直径,高是圆的半径。
圆比正方形多的面积:3.14 - 2=1.14(m )
圆的面积:3.14×1 =3.14(m )
阴影部分的面积=圆的面积-正方形的面积
×(2×1)
×2
=2(m )
正方形的面积:
“外圆内方”
左图:(2r ) -π×r =(4-π)r
右图:π×r -( ×2r ×r )×2=(π -2)r
回顾与反思
如果两个圆的半径都是r,结果又是怎样的?
掌握组合图形的特征,能灵活的计算其中的部分的面积。
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24cm。外面的圆与内部的正方形之间的面积是多少?
圆的面积:3.14×(24÷2) =452.16(cm )
正方形的面积: ×24 × 12 × 2=288(cm )
圆比正方形多的面积:452.16-288=164.16(cm )
答:外面的圆与内部的正方形之间的面积是164.16 cm 。
2.王师傅做一个零件,零件的形状是圆内接正方形,已知圆的直径为12 cm,你能计算出正方形的面积吗?
答:正方形的面积是72cm 。
圆的半径:12÷2=6(cm)
正方形的面积:
×6 × 12 × 2=72(cm )
1
2
3.求下面涂色部分的面积。
圆面积:
3.14×(40÷2)2
=3.14×400
=1256(平方厘米)
正方形面积:
40×40=1600(平方厘米)
涂色部分面积:
1600-1256=344(平方厘米)
4.求图中阴影的面积。
空白部分面积:10 -10 ×3.14×0.25
阴影部分的面积:10 -43=57(平方厘米)
=100-78.5
21.5×2=43(平方厘米)
=21.5(平方厘米)
阴影部分的面积=正方形的面积-空白部分的面积。
生活数学
5.有一栋底面呈长方形的建筑物(如下图),墙角有一根木桩,木桩上拴着一条狗。拴狗的绳子长4 m,这条狗活动区域的面积有多大
1.在正方形内画一个最大的圆,正方形和圆
之间部分的面积为:
2.在圆内画一个最大的正方形,正方形和圆
之间部分的面积为:
S正-S圆
S圆-S正
